文章信息
- 李晓伟, 王炜, 杨敏, 王昊, 徐铖铖
- LI Xiaowei, WANG Wei, YANG Min, WANG Hao, XU Chengcheng
- 现代有轨电车选线测度模型与应用
- Route selection model of modern streetcar and its application
- 武汉大学学报(工学版), 2017, 50(5): 720-726
- Engineering Journal of Wuhan University, 2017, 50(5): 720-726
- http://dx.doi.org/10.14188/j.1671-8844.2017-05-013
-
文章历史
- 收稿日期: 2016-12-20
2. 西安建筑科技大学土木工程学院,陕西 西安 710055;
3. 东南大学现代城市交通技术协同创新中心,江苏 南京 210096;
4. 西安建筑科技大学西部建筑科技国家重点实验室,陕西 西安 710055
2. School of Civil Engineering, Xi'an University of Architecture & Technology, Xi'an 710055, China;
3. Collaborative Innovation Center of China's Modern Traffic Technology, Southeast University, Nanjing 210096, China;
4. State Key Laboratory of Architecture Science and Technology in West China, Xi'an University of Architecture and Technology, Xi'an 710055, China
现代有轨电车具有节能、环保、舒适与灵活性高等特点,正以崭新的形象和显著的优势重新出现在城市中.我国《国民经济和社会发展十二五规划纲要》中指出,各城市应该根据自身规模和特点,制定差别化的轨道交通发展目标,有序推进轻轨、地铁、有轨电车等城市轨道交通网络建设.作为一种新兴的公共交通工具,有轨电车逐渐成为我国缓解城市内日益严峻的交通拥堵和环境污染问题的重要途径之一.截止2020年,我国有轨电车的规划里程已经超过2 500 km.中国现代有轨电车工程正处于大规模、高速度、超常规建设的前夜.
目前国外针对有轨电车的研究主要集中在运营管理等方面.A. S. Shalaby等人以有轨电车站点停靠时间为研究对象,利用加拿大Toronto市有轨电车实测数据对电车运行进行了模拟,提出了降低有轨电车站点停靠延误的方法[1];A. Molecki等人基于Monte Carlo法[2]综合处理影响有轨电车运行的诸因素,建立了一种考虑轨道容量、站点、交叉口和信号灯的有轨电车运量计算模型[3];T. Nakashi等人提出一种有轨电车运行时刻表自动复原模型,用于处理有轨电车到站时间偏离到站时刻表等异常情况下的系统恢复问题[4].国内针对有轨电车的研究则处于起步阶段,主要集中在应用模式[5]、融资模式[6]、站线设计[7]及信号控制[8]等方面,如李际胜等对有轨电车车站、线路布置形式、交通组织设计等方面进行了探讨,鲜有对有轨电车选线理论的研究.
本文在总结多个城市有轨电车选线思路的基础上,深入分析了现代有轨电车选线因素,包括与城市发展的协调性、客流吸引能力、道路交通条件及成本、效益,明确了选线准则及测度方法;并将多目标格序决策理论应用到有轨电车路线方案选择过程,建立了有轨电车路线优选模型,为我国有轨电车项目路线方案选择的科学化决策提供合理、可靠的依据.
1 有轨电车选线准则与量化 1.1 选线思路现代有轨电车的线路设置依托于城市总体规划,结合城市路网特征、最大客流方向和主要客流集散点,将住宅区、商业街区、工业、企业及机关事业单位等公共设施集中地、旅游地、交通枢纽联系起来,为居民出行提供便捷的交通服务,减少出行时间.
有轨电车的选线具有总体性、复杂性、阶段性特征,是一项涉及多专业、多部门集体协调、研究的系统工程.在有轨电车选线过程中,首先,要全面研究线路相关资料,彻底了解有轨电车在城市综合交通系统中的走向、换乘关系、功能定位、站点分布.其次,踏勘核对路线场地,掌握沿线道路、建筑物、交通情况,落实规划线位的可实施性,找出控制线位的控制点与备选方案,综合协调线位与站位的匹配[9].有轨电车选线的方法与流程可总结为[7]:
1) 遵循规划要求:线路走向及车站布置应符合城市总体规划及多模式公交发展规划需要,符合城市总体规划和有轨电车线网规划的要求.
2) 满足客流需求:线路走向及车站布置应与城市主导客流方向一致,实现与其他交通方式的良好衔接,与城市综合交通规划相协调,为乘客提供便捷的换乘环境,以利于最大限度吸引客流,提高运营效益.
3) 合理利用城市空间:线路走向应充分考虑既有及规划的建筑物、构筑物、地面交通等对线站位置的影响,尽量将线站布置在施工条件好、拆迁量小、对市政设施干扰小的地带.
4) 结合道路横断面形式:线路平面力求顺直,提高乘客的舒适度;综合考虑城市道路的横断面形式,减少对道路交通的干扰,达到建设和运营的经济性.
5) 节省造价:线路走向及车站布置要结合沿线地形、地貌等实际情况,尽量采用地面线,以降低施工难度和节省工程投资.
6) 保护环境和景观:线站平面布置及敷设方式要注意对城市环境的保护,以及与道路景观的融合.
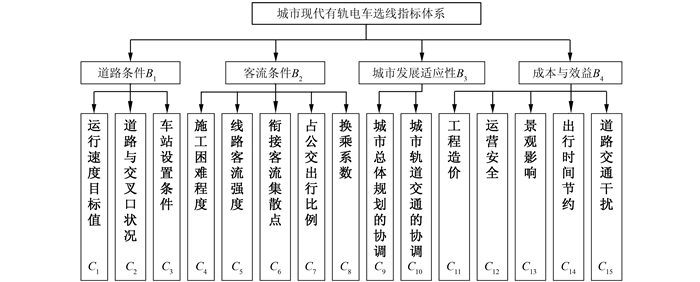
1.2 选线准则及其量化建立城市有轨电车选线影响因素指标体系时,一是借鉴国内各大中城市(南京、苏州、上海、天津)地铁、轻轨、有轨电车选线时常采用的指标;二是参考有轨电车勘察设计人员、专家、学者对有轨电车选线因素的判断.综合分析现代有轨电车路线准则及影响因素,可将有轨电车选线指标划分为道路条件、客流条件、城市发展适应性、成本与效益四个准则[9-12].具体量化指标如图 1所示.
|
| 图 1 城市现代有轨电车选线指标体系 Figure 1 Route choice indexes system for urban modern streetcar |
其中定量指标包括运行速度目标值C1、线路客流强度C5、衔接客流集散点C6、占公交出行比例C7、换乘系数C8、工程造价C11、出行时间节约C14等指标.运行速度目标值C1是指有轨电车在选定的线路区间内可运行的平均速度(运行时间包括中间站停站时间和启停车附加时间);线路客流强度C5是指单位有轨电车线路长度上的乘客总量;衔接大型客流集散点C6指有轨电车与大型客流集散点的衔接数量;占公交出行比例C7是有轨电车出行量与公交出行量之间的比值;换乘系数C8是指有轨电车客流总量与有轨电车出行OD总量的比值;有轨电车建设费用C11是指有轨电车建设里程乘以单位造价,为避免与施工难易程度指标的重复,有轨电车建设费用采用平均区间价格;出行时间节约C14为无有轨电车情况下的居民公交平均出行时间减去有有轨电车情况下的居民公交平均出行时间.
定性指标量化采用群专家决策法确定,具体量化标准如表 1所示,计算公式为
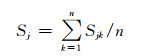 (1)
(1)
| 有轨电车选线定性指标 | 分值 | |||||||
| C2 | C3 | C4 | C9 | C10 | C12 | C13 | C15 | |
| 很不好 | 很不好 | 很不好 | 很不好 | 很不好 | 严重影响 | 严重影响 | 很不安全 | 0~25 |
| 不好 | 不好 | 不好 | 不好 | 不好 | 明显影响 | 明显影响 | 不安全 | 25~40 |
| 中等 | 中等 | 中等 | 中等 | 中等 | 轻微影响 | 轻微影响 | 中等 | 40~60 |
| 好 | 好 | 好 | 好 | 好 | 基本无影响 | 基本无影响 | 安全 | 60~80 |
| 非常好 | 非常好 | 非常好 | 非常好 | 非常好 | 无影响 | 无影响 | 非常安全 | 80~100 |
其中:n为群体专家人数;Sj为定性指标Cj的评估值;Sjk为第k个专家对定性指标Cj的评估值.
2 选线模型格序决策主要用于解决非全序性刻画的复杂系统择优排序问题,决策者对不同决策方案的偏好元素构成一个格,格序比全序更真实地反映决策者的偏好结构,因而对于多目标多元素的复杂系统择优比选问题,格序决策较全序决策更加科学合理[13-15].
2.1 原始矩阵构建若评价方案为Ai(i=1, 2, …, m), 评价指标为Cj(j=1, 2, …, n), 则各方案指标原始矩阵为
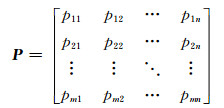 (2)
(2)
式中: pij为第i个方案Ai的相对于第j个指标Cj的评价值.
2.2 指标无量纲化由于不同的指标具有不同单位,缺乏公度性,故需对指标评测数据分正向指标、逆向指标分别进行无量纲化处理[16], 具体如下.
对于正向型指标:
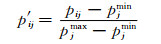 (3)
(3)
对于负向型指标:
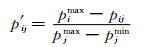 (4)
(4)
式中: p′ij为无量纲化处理后的指标值;pij为评测指标原始值;pjmax为评价指标Cj上限值;pjmin为评价指标Cj下限值.
2.3 权重的确定权重的计算方法主要有主观判断与客观分析两类,主观判断法过度依赖于专家经验,客观分析法往往容易忽视专家的知识与经验,计算结果与实际背离较大.鉴于上述不足,本文将上述两类方法用组合法予以有效结合.
2.3.1 客观权的确定设评价指标客观离散度权向量[17]为
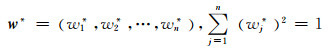
λij(wj*)表示第i项评价方案的第j个评价指标与该指标其他方案评价值的离差之和,即
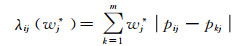 (5)
(5)
λj(wj*)表示在第j个评价指标下,所有评价方案的总离差,即:
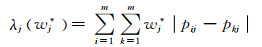 (6)
(6)
根据离差最大化确定权重的原理,评价指标的权重应该使所有评价指标的总离差最大.即使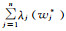
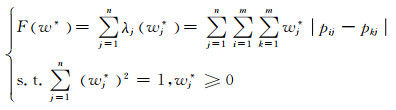 (7)
(7)
解式(7), 并进行归一化处理, 得客观权向量为
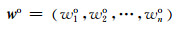 (8)
(8)
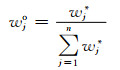 (9)
(9)
运用层次分析法(AHP)对专家的定性评判进行处理, 得到主观权向量为
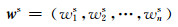 (10)
(10)
某项指标的总权重应与主观权与客观权相关, 出于这一考虑, 定义总权向量为
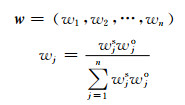 (11)
(11)
定义算子dij=wjp′ij, 则决策矩阵为
 (12)
(12)
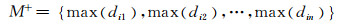 (13)
(13)
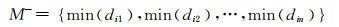 (14)
(14)
正、负理想解间欧氏距离为
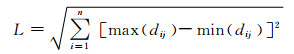 (15)
(15)
方案i与正、负理想解间欧氏距离分别为
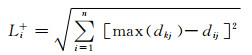 (16)
(16)
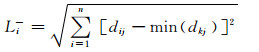 (17)
(17)
定义方案i的综合差异值为
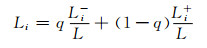 (18)
(18)
式中:q为乐观系数,0 < q < 1,一般取q=0.5.依据Li的大小,可对方案予以优选.
3 实证研究 3.1 提出方案根据技术可行、实施可能的原则,充分考虑已探明工程地质、水文地质条件, 兼顾工程量的大小、施工难易程度及今后的营运管理,尽量做到降低造价, 保证设计与施工质量.根据当地实际情况,某市有轨电车1号线共提出4个路线方案,根据路线方案指标的量化方法,4个备选方案指标的属性值如表 2所示.
| 指标 | B1 | B2 | B3 | B4 | ||||||||||||||
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | C13 | C14 | C15 | ||||
| A1 | 31 | 22 | 80 | 60 | 0.56 | 19 | 82 | 1.30 | 50 | 70 | 12 | 85 | 50 | 29 | 82 | |||
| A2 | 27 | 25 | 85 | 84 | 0.79 | 25 | 86 | 1.20 | 70 | 80 | 15 | 80 | 72 | 31 | 68 | |||
| A3 | 19 | 27 | 82 | 40 | 0.96 | 17 | 80 | 1.25 | 80 | 85 | 15 | 60 | 75 | 15 | 60 | |||
| A4 | 26 | 30 | 76 | 75 | 0.64 | 21 | 75 | 1.40 | 75 | 78 | 14 | 70 | 68 | 27 | 70 | |||
将线网评价指标进行归类整理, 并划分为正向指标集、负向指标集.正向指标集包含的元素有运行速度目标值、道路及交叉口状况、车站设置条件、施工困难程度、线路客流强度、衔接客流集散点、占公交出行比例、城市总体规划的协调、城市轨道交通的协调、运营安全、景观影响、出行时间节约、道路交通干扰等指标;负向指标集包含换乘系数、工程造价.应用式(3)、(4),经归一化处理得表 3.
| 指标 | B1 | B2 | B3 | B4 | ||||||||||||||
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | C13 | C14 | C15 | ||||
| A1 | 1.00 | 0 | 0.44 | 0.46 | 0 | 0.25 | 0.64 | 0.50 | 0 | 0 | 1.00 | 1.00 | 0 | 0.88 | 1.00 | |||
| A2 | 0.67 | 0.38 | 1.00 | 1.00 | 0.58 | 1.00 | 1.00 | 1.00 | 0.67 | 0.67 | 0.11 | 0.80 | 0.88 | 1.00 | 0.36 | |||
| A3 | 0 | 0.63 | 0.67 | 0 | 1.00 | 0 | 0.46 | 0.75 | 1.00 | 1.00 | 0 | 0 | 1.00 | 0 | 0 | |||
| A4 | 0.58 | 1.00 | 0 | 0.80 | 0.20 | 0.50 | 0 | 0 | 0.83 | 0.53 | 0.44 | 0.40 | 0.72 | 0.75 | 0.45 | |||
指标权重的确定,主观权重采用AHP法,客观权重及综合权重运用式(5)~(11),并结合表 3中相关指标数据求得,结果见表 4、5.
| 准则层 | ws | wo | w |
| B1 | 0.16 | 0.267 | 0.214 |
| B2 | 0.46 | 0.266 | 0.363 |
| B3 | 0.10 | 0.133 | 0.117 |
| B4 | 0.28 | 0.134 | 0.207 |
| 指标 | B1 | B2 | B3 | B4 | ||||||||||||||
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | C13 | C14 | C15 | ||||
| wo | 7.4 | 4.3 | 2.4 | 1.9 | 20.7 | 5.1 | 5.1 | 8.3 | 6.7 | 3.3 | 9.8 | 7.1 | 2.2 | 4.8 | 3.9 | |||
| ws | 6.7 | 6.6 | 6.6 | 6.8 | 6.7 | 6.7 | 6.6 | 6.6 | 6.7 | 6.6 | 6.6 | 6.7 | 6.7 | 6.8 | 6.6 | |||
| w | 7.1 | 5.5 | 4.5 | 4.5 | 13.7 | 5.9 | 9.4 | 7.5 | 6.7 | 5.0 | 8.2 | 6.9 | 4.5 | 5.8 | 5.3 | |||
运用式(12), 结合表 3、5中数据, 计算得加权决策矩阵, 见表 6.
| 指标 | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | C13 | C14 | C15 |
| A1 | 7.10 | 0 | 1.98 | 2.1 | 0 | 1.47 | 6.02 | 3.75 | 0 | 0 | 8.20 | 6.90 | 0 | 5.10 | 5.30 |
| A2 | 4.76 | 2.09 | 4.50 | 4.5 | 7.95 | 5.90 | 9.40 | 7.50 | 4.49 | 3.35 | 0.90 | 5.52 | 3.96 | 5.80 | 1.91 |
| A3 | 0 | 3.47 | 3.02 | 0 | 13.70 | 0 | 4.32 | 5.63 | 6.70 | 5.00 | 0 | 0 | 4.50 | 0 | 0 |
| A4 | 4.12 | 5.50 | 0 | 3.6 | 2.74 | 2.95 | 0 | 0 | 5.56 | 2.65 | 3.61 | 2.76 | 3.24 | 4.35 | 2.39 |
根据表 6,应用式(13)~(14)解得正负理想解后代入式(15)~(18)求得各方案与正负理想解间的欧氏距离及各方案综合差异值, 计算结果见表 7.基于综合差异值, 该市有轨电车1号线最优路线方案为方案2,为最终实施方案.方案2中有C3、C4、C6、C7、C8、C14等6个指标在4个方案中均为最优,C1、C5、C10、C12、C13等5个指标在4个方案中均名列第2,研究结果具有合理性.
| Ai | A1 | A2 | A3 | A4 |
| L+ | 0.191 | 0.112 | 0.178 | 0.189 |
| L- | 0.167 | 0.205 | 0.186 | 0.131 |
| 综合差异值 | 0.466 | 0.647 | 0.512 | 0.410 |
1) 有轨电车选线主客观确权比较研究.根据表 3可知,应用客观权重法确定的各指标权重之间的偏差很小,基本上在0.06~0.08之间浮动,这是因为本文的客观权重法(离差最大化法)是根据各方案该指标的离差之和决定因素的重要程度.由于各方案指标之间的离差之和相近,因此各指标权重之间的偏差不大,难以有效反映各指标在有轨电车选线过程中的重要程度,需要考虑有轨电车专家学者及工作人员对有轨电车选线因素重要度的主观判断.研究结果表明:有轨电车选线过程中,各指标权重的确定既需要考虑方案数据本身蕴含的信息,同时也要考虑专家学者及工作人员的经验判断,综合主客观权重才能更加科学合理地对有轨电车选线因素进行确权.
2) 有轨电车选线因素重要度研究.应用综合权重法对有轨电车各选线因素进行确权分析,准则中客流条件的权重指数为0.363,其次为道路条件、成本效益和城市发展适应性,分别为0.214、0.207和0.117,这说明在有轨电车选线过程中首先应考虑有轨电车线路的客流状态,这与我国建设有轨电车以缓解城市道路交通压力的实际契合.同时,在指标层中,指标权重较大的分别是线路客流强度、占公交出行比例、工程造价及运行速度目标值,这说明在我国交通拥堵的现实国情下,在兼顾成本与效率的基础上大幅度吸引客流、缓解交通拥堵是有轨电车建设的主要目的.
3) 有轨电车选线模型研究.应用多目标格序决策理论构建有轨电车选线模型,并对其评价方法与流程结合实例进行了有益的尝试.通过对各方案综合差异的求解,实现了方案的优劣性排序;采用合成法计算了各指标的综合权重,实现了主观权重与客观权重的有效衔接与统一;通过与实际项目评价结果的对比,证明了该方法的合理性;实例研究表明该模型能够为有轨电车的规划选线提供科学合理的决策依据.
| [1] | Shalaby A S, Ling K, Sinikas J. Multiple-unit streetcar operation: Evaluation using microsimulation modeling[C]// 85th Annual Meeting of the Transportation Research Board, Washington D C, 2006. |
| [2] | Fisz M. Probability Theory and Mathematical Statistics[M]. New York: Wiley, 1963. |
| [3] | Molecki A, Gaska D. Calculations of tramway track capacity in the wide area networks[J]. Transport, 2012, 27(4): 428–433. DOI:10.3846/16484142.2012.754378 |
| [4] | Nagatani T. Dynamical model for retrieval of tram schedule[J]. Physica A: Statistical Mechanics and its Applications, 2007, 377(2): 661–671. DOI:10.1016/j.physa.2006.11.029 |
| [5] |
訾海波, 过秀成, 杨洁. 现代有轨电车应用模式及地区适用性研究[J].
城市轨道交通研究, 2009(2): 46–49.
Zi Haibo, Guo Xiucheng, Yang Jie. On the application mode and adaptablity of modern streetcar[J]. Urban Rail Transit, 2009(2): 46–49. |
| [6] |
韩铁莲. 三亚现代有轨电车项目融资模式研究[D]. 长春: 吉林大学, 2014.
Han Tielian. The financing mode of Sanya modern tram project[D]. Changchun: Jilin University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10183-1014211779.htm |
| [7] |
李际胜, 姜传治. 有轨电车线站布置及交通组织设计[J].
城市轨道交通, 2007(5): 38–41.
Li Jisheng, Jiang Chuanzhi. Line and station planning and traffic organization of light rail transit[J]. Urban Rail Transit, 2007(5): 38–41. |
| [8] |
钟吉林. 干线信号协调下的有轨电车优先研究[D]. 成都: 西南交通大学, 2014.
Zhong Jilin.Tram signal priority under arterial signal coordination[D]. Chengdu: Southwest Jiaotong University, 2014. http://cdmd.cnki.com.cn/article/cdmd-10613-1014254764.htm |
| [9] |
陈剑伟. 城市轨道交通线路设计方法[J].
铁道工程学报, 2013, 181(10): 96–101.
Chen Jianwei. Research on track design method for urban rail transit[J]. Journal of Railway Engineering Society, 2013, 181(10): 96–101. DOI:10.3969/j.issn.1006-2106.2013.10.020 |
| [10] |
何宁, 潘向阳. 城市快速轨道交通规划的决策分析研究[J].
中国公路学报, 1999, 12(3): 73–81.
He Ning, Pan Xiangyang. The decision-making research on urban rapid rail transit planning[J]. China Journal of Highway and Transport, 1999, 12(3): 73–81. |
| [11] |
汪涛. 城市轨道交通建设方案评价方法研究[J].
铁道工程学报, 2011(4): 88–93.
Wang Tao. Research on evaluation methods for urban rail transit construction projects[J]. Journal of Railway Engineering Society, 2011(4): 88–93. |
| [12] |
陶克, 吴小萍. 城市轨道交通网络规划的优选决策研究[J].
武汉理工大学学报(交通科学与工程版), 2010, 34(3): 608–615.
Tao Ke, Wu Xiaoping. Research on urban mass transit transportation network planning optimization decision-making[J]. Journal of Wuhan University of Technology (Traffic Science and Engineering Edition), 2010, 34(3): 608–615. |
| [13] |
刘玉增, 钱丙益. 轨道交通线网方案比选的多目标格序决策方法[J].
交通运输工程学报, 2011, 11(5): 76–82.
Liu Yuzeng, Qian Bingyi. Multi-objective lattice-order decision-making method of scheme selection for rail transit network[J]. Journal of Traffic and Transportation Engineering, 2011, 11(5): 76–82. |
| [14] |
李晋, 钱秉毅. 基于格序理论的爆炸类危险化学品运输路径研究[J].
中国安全科学学报, 2011, 21(4): 137–142.
Li Jin, Qian Bingyi. Study on optimal route selection for explosive hazardous chemicals transportation based on lattice order decision making theory[J]. China Safety Science Journal, 2011, 21(4): 137–142. |
| [15] |
涂圣文, 过秀成, 刘海强. 干线公路城市过境方案决策的灰色格序方法[J].
公路交通科技, 2013, 20(7): 119–125.
Tu Shengwen, Guo Xiucheng, Liu Haiqiang. A grey lattice order decision-making method for scheme of arterial highway passing through city nodes[J]. Journal of Highway and Transportation Research and Development, 2013, 20(7): 119–125. |
| [16] |
李晓伟, 陈红, 马娟, 等. 基于TOPSIS的公路建设项目排序方法及应用[J].
长安大学学报(自然科学版), 2012, 32(3): 49–52.
Li Xiaowei, Chen Hong, Ma Juan, et al. Priority method and its application in highway construction based on TOPSIS[J]. Journal of Chang'an University (Naturnal Science Edition), 2012, 32(3): 49–52. |
| [17] |
肖新平, 李福琴, 涂金忠. 基于离差最大化的灰色关联分析法在公路网综合评价中的应用[J].
公路, 2006(8): 122–126.
Xiao Xinping, Li Fuqin, Tu Jinzhong. Application of grey relational analysis based on maximizing deviations to comprehensive evaluation for highway network[J]. Highway, 2006(8): 122–126. |
| [18] |
李晓伟, 陈红, 邵海鹏, 冯志慧. 基于累积前景理论的公路建设项目灰关联排序模型[J].
公路交通科技, 2011, 28(10): 132–135.
Li Xiaowei, Chen Hong, Shao Haipeng, Feng Zhihui. Grey correlation priority decision model of highway construction project based on cumulative prospect theory[J]. Journal of Highway and Transportation Research and Development, 2011, 28(10): 132–135. |
| [19] |
王念念. 城市轨道交通规划线网综合评价研究[D]. 北京: 北京交通大学, 2007.
Wang Lianlian. Comprehensive evaluation of urban rail transit network plan[D]. Beijing: Beijing Jiaotong University, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10004-2007048610.htm |
| [20] |
周明保, 黄亮, 张宁, 杨利强. 轨道交通票制选择多层多属性决策模型[J].
东南大学学报(自然科学版), 2010(40): 316–320.
Zhou Mingbao, Huang Liang, Zhang Ning, Yang Liqiang. Multi-level multi-attribute decision-making model for choice of fare collection pattern in urban rail transit[J]. Journal of Southeast University (Natural Science Edition), 2010(40): 316–320. |
 2017, Vol. 50
2017, Vol. 50




