文章信息
- 陈雨豪, 周黎, 郭为安, 于颖
- CHEN Yuhao, ZHOU Li, GUO Weian, YU Ying
- 面向舞蹈机器人步态控制的膝关节参数粒子群优化
- Particle swarm optimization of knee joint parameters for dancing robot walking gait
- 武汉大学学报(工学版), 2018, 51(2): 178-182, 188
- Engineering Journal of Wuhan University, 2018, 51(2): 178-182, 188
- http://dx.doi.org/10.14188/j.1671-8844.2018-02-013
-
文章历史
- 收稿日期: 2017-05-15
2. 同济大学中德工程学院,上海 201804
2. Sino-German College of Applied Sciences, Tongji University, Shanghai 201804, China
在当前娱乐文化以及教育产业中,舞蹈机器人得到了广泛应用.在舞蹈机器人的动作控制中,包括行走、跳跃等基本动作的实现是完成预定编舞动作的基础.因此,机器人的步态控制技术备受关注,引起了国内外众多学者们的高度关注.李建等人提出了一种凹凸地面上双足机器人的步行控制算法.该算法分为两个方面:步态规划和在线反馈控制系统,都是旨在使机器人在任何起伏地形上能够高效稳定地行走[1].谭建豪等人提出基于学习人类控制策略的双足机器人步态控制方法,提高了双足机器人在复杂环境行走的动态稳定性[2].王丽杨等人提出能耗预估策略和能效优化算法,获得满足零力矩点稳定判据的低能耗步态,有效地优化了机器人的能耗和稳定性[3].王立鹏等人提出一种零冲击的足端轨迹规划改进算法, 并实现了步态规划算法设计,设计了一种液压四足机器人仿生机构.仿真试验结果证明了该足端轨迹规划方法用于四足机器人步态设计的合理性和有效性[4].杨贵志等人根据生物CPG机制的分层结构和运动神经元的功能, 提出一个有层次化结构的CCPG模型, 旨在解决CCPG模型难以生成相位协调的多自由度运动控制信号的问题[5].张国腾等人提出了支撑相虚拟模型控制方法和摆动相虚拟模型控制方法,使机器人能够以对角小跑步态在平地上进行全方位移动, 跨越不平坦地形, 并能够抵抗外部冲击[6].蔡楷旋等人通过运用ADAMS虚拟样机技术仿真机器人在空中踏步和地面运动的腿运动学得到的运动图源数量和形状,得出有较低复杂性的模块和前馈电机控制是能足够满足被动顺从的腿硬件系统的地面运动的结论[7].丁家涛等人提出一种步态生成与偏航行走控制策略, 实现步态模式的在线生成与自主偏航行走[8].李攀等人通过三次样条插值方法对双足机器人进行完整的步态规划, 得到机器人各关节平滑的运动轨迹[9].
然而,以上研究中缺乏机器人的拟人步态控制研究,即机器人步态与人类步态的拟态研究较为匮乏.本文通过对机器人膝关节进行非线性控制,利用对人为姿态的模拟实现对机器人步态的协调,实现机器人步态对人类步态的自然模拟,对机器人在舞蹈教学以及表演等方面具有重要意义.
对于膝关节控制的非线性时变问题,其数学分析难度以及控制的难度较高,数学分析难度较大.求解过程中需要对模型具有导数信息等数学条件,这给舞蹈机器人对不同人员的步态模拟带来了挑战.为了使得机器人能够便捷地模拟不同人体步态,启发式优化方法受到了国内外学者们的青睐.包括遗传算法、模拟退火等不同的启发式方法在机器人位姿轨迹跟踪与优化问题中均具有良好的性能表现[10-13],其主要技术路线是将控制优化转变成参数优化相关的问题.
行走步态是舞蹈机器人的常见动作,舞蹈机器人的步态拟人化能够产生更加逼真的艺术效果.本文通过对人类行走过程中膝关节部位的模拟实现机器人拟人化的步态控制,实现机器人步态控制信号的参数化,将机器人的步态控制转化为参数优化问题,通过模拟人类步态构建适应度函数,利用启发式优化算法对适应度函数进行求解,找到能产生最佳控制的参数,从而模拟人类的步态行为.
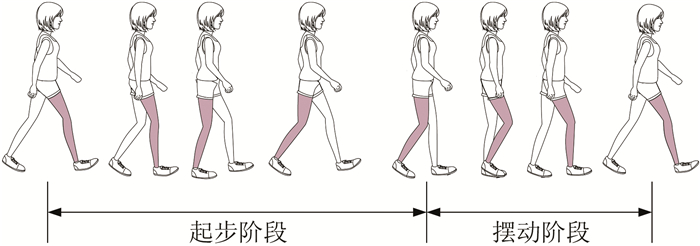
1 问题描述机器人在行走过程中,其行走步态的循环包括两部分:起步阶段和摆动阶段.起步阶段为脚部与地面的接触阶段,始于脚后跟第一次接触地面,止于脚部抬离地面.摆动阶段为脚部与地面无接触的阶段,在行走过程中紧随着起步阶段之后.图 1为人类步态循环的起步阶段和摆动阶段示意图.
|
| 图 1 人类行走中步态的“起步阶段”和“摆动阶段”示意图 Figure 1 Stance phase and swing phase during a gait |
由机器人运动学方程可知[14],其运动的基本形式为
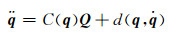 (1)
(1)
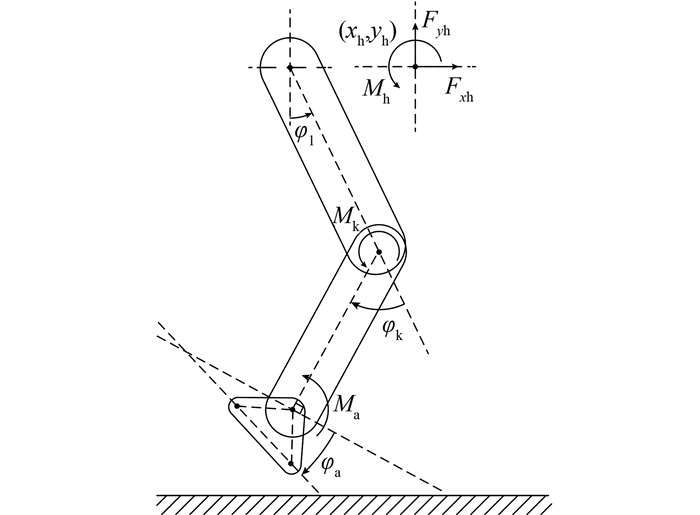
其中:q为模型运动自由度的向量,qT=[xh yh φ1 φk φa];Q为单个自由度的动作矢量,QT=[Fxh Fyh Mh Mk Ma];xh为臂部水平位置,yh为臂部竖直位置;φ1为大腿夹角,φk为膝部夹角,φa脚踝夹角;Fxh为臂部水平力,Fyh为臂部竖直力;Mh为臂部力矩,Mk为膝部力矩,Ma为脚踝力矩.各变量表示的角与力的图示说明参见图 2.
|
| 图 2 腿部关节示意图 Figure 2 Figure of robot's leg joint |
本文使用线性液压执行器为假体提供膝关节转矩,其驱动器为机械装置,用以控制步态循环中膝关节运动中的能量,进而使得液压执行器在没有外部电源的条件下,给膝关节提供扭矩与阻尼,整个过程中膝关节是唯一需要进行控制的环节.相比于完全主动式动力关节控制方法,本文所使用的控制方案能够大大减小对能量的需求.驱动器的模型为
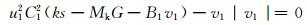 (2)
(2)
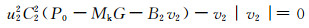 (3)
(3)
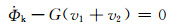 (4)
(4)
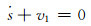 (5)
(5)
式(2)~(4)中:B1为通过阀门1的恒定粘性阻力,B2为通过阀门2的恒定粘性阻力;C1为阀门1的最大截面积,C2为阀门2的最大截面积;G为瞬时压力比;k为高压蓄能弹簧弹性;P0为低压蓄能器的压力;s为高压流体体积;u1为阀1的控制归一化到[0, 1];u2为阀2的控制归一化到[0, 1];v1为通过阀门1向上流体流速.
相关的膝关节执行器动力学方程参见文献[15].
不同执行器之间的区别在于压力比G,该数值非常数,与膝关节角度相关.相关描述膝关节执行器动力学的推导可参见文献[15],该文献中提供了详细的拟人步态数据.本文将被模仿者的臀部位置、膝盖处和大腿处所产生的夹角作为机器人下肢运动控制器的参考轨迹.控制器设计如图 3所示,该控制器能够有效地获取膝盖与大腿之间的角度以及起步阶段的臀部位置.
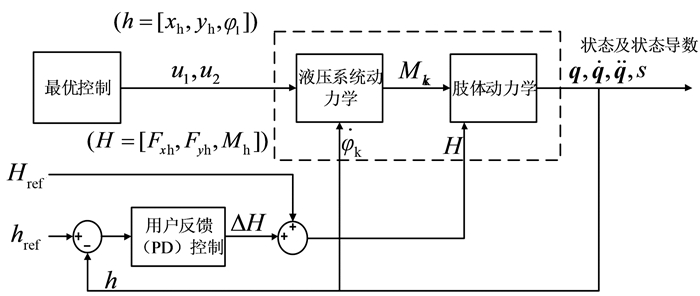
|
| 图 3 控制器设计图 Figure 3 Design of controller |
本文利用比例微分反馈控制器模拟退步产生的力与力矩,利用运动过程中臀部位置以及大腿位置的角度误差实现跟踪控制.其行为的表达式如下:
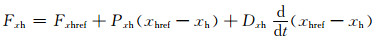 (6)
(6)
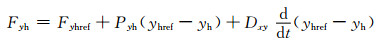 (7)
(7)
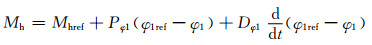 (8)
(8)
其中:下标ref表示对应的参考点取值.考虑到双足机器人在行走过程中,双脚需要分别且并行地经历起步阶段和摆动阶段.当一只腿处于起步阶段仍然与地面接触时,另一只腿在空中摆动.起步阶段与摆动阶段的力及力矩均不相同,因此本文设计不同的控制器增益.在起步阶段,机器人无法提供较大的驱动补偿,于是在该阶段本文使用较低的控制器增益,而在摆动阶段则使用较高的控制器增益.
2 优化方法设计本文以100 Hz的控制更新频率在离散时间内对机器人膝关节进行控制.开环控制由两个控制信号序列组成,分别是u1和u2,分别对应两个液压控制阀.阀的完全闭合与完全打开,分别在控制信号中用0和1来表示.本文采取粒子群优化方法来求解非线性时变系统.由于除了高压蓄电池供给的弹簧之外没有其他能量来源为膝盖处提供转矩,这意味着一旦耗尽储存能量,或者将能量供给能力降低到特定值,就会有可能导致义肢无法站立,膝盖处角度低于零度,或导致系统对角度捕捉能力降低等情况,所以我们必须有选择地对能量进行储存与释放.
2.1 粒子群优化方法简介粒子群优化(Particle Swarm Optimization,PSO)方法最早由Kennedy和Eberhart等人通过模拟鸟群飞行行为所提出[16],近年来在理论发展以及实际应用中受到广泛关注.在粒子群算法中,群体由一组粒子构成,每个粒子包括粒子位置和粒子速度两个变量.通过构造位置与速度的更新方式,不同粒子之间进行直接或间接的交互.粒子速度的演变主要受到3方面的影响,分别是当前速度、当前位置与历史最好位置的距离,以及当前位置与全局最优位置的距离.粒子的位置更新受到粒子速度更新与当前位置的影响.具体的粒子位置与速度更新公式如下:
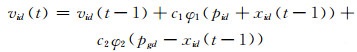 (9)
(9)
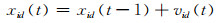 (10)
(10)
其中:vid是第i个粒子的速度;pid是第i个粒子的自身历史最优位置;pgd是当前种群的全局最优位置;xid是第i个粒子在t时刻的位置.
2.2 优化目标在完整的步态循环中,机器人步态的控制由两个液压阀控制信号组成,本文通过对10名志愿者的数据采集,获得一个步态循环时间约为1.21 s.由于本文的控制信号频率为100 Hz, 因此每个控制信号包括121个变量.如此规模的变量将增大粒子群优化的搜索空间复杂度,因此,本文通过对控制信号进行傅里叶级数变换,保证控制信号在连续可导的周期函数中估值到任意精度.以u1控制信号为例,其表达式如下:
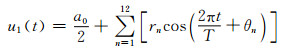 (11)
(11)
其中:0≤a0≤2, 0≤rn≤1, -π≤θn≤π, n>0.为简化控制系统,本文仅展开至基频进行分析,仿真结果表明该模型可以达到预期控制效果.鉴于本文的控制信号为0-1,因此通过对粒子群的可行解在0-1空间内进行编码即可获得最优控制方案.相关系数值范围的制定能够在期望性能和计算量之间得到适当的平衡.通过对控制信号进行傅里叶级数展开,即可以仿真零阶保持微控制器的运算.所构造的步态循环的起始与终止时刻之间的不同电压、腿部、脚踝以及膝关节部的跟踪误差(包括膝盖角度低于零度(极限延伸)情况发生的次数等)表达式如下所示:
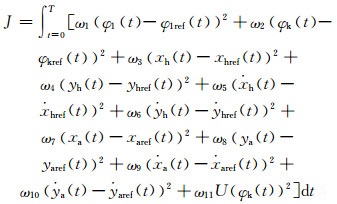 (12)
(12)
其中:φkref为膝盖角度参考值;xhref和yhref为大腿部位参考值;xaref和yaref为脚踝部位对应参考值;ωi(i=1, 2, …, 11)用于控制不同变量的精度要求,ωi越大表明该项的控制精度要求越高,在后文的仿真试验中,ωi均设置为1,即对于不同的控制变量在本文中的控制精度要求均相同.优化目标即为最小化式(12)所示的跟踪误差.
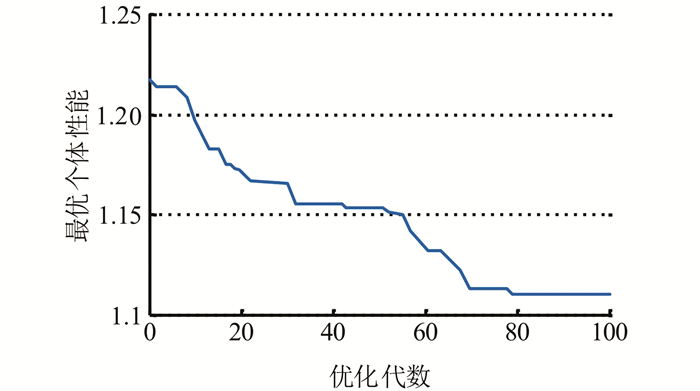
2.3 开环控制结果利用粒子群优化方法对式(12)中的优化变量进行求解.为了拓宽搜索空间和仿真算法陷入局部最优,个体利用了采用1%比例的变异率,为了防止丢失全局最优解,算法在优化过程中采用精英策略.图 4显示PSO算法每一代中最优个体的性能.
|
| 图 4 粒子群算法迭代过程中最优个体的适应度值 Figure 4 Fitness of the best individual during PSO iterations |
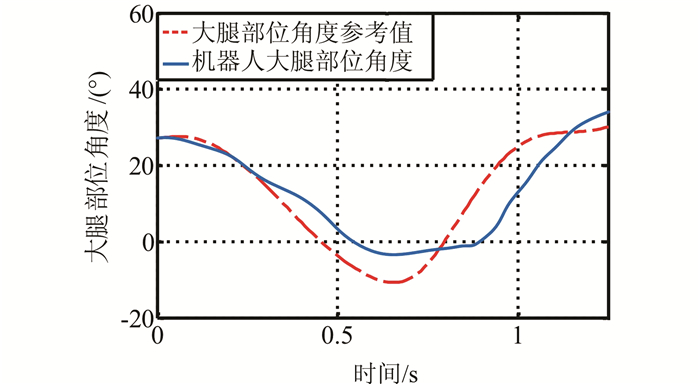
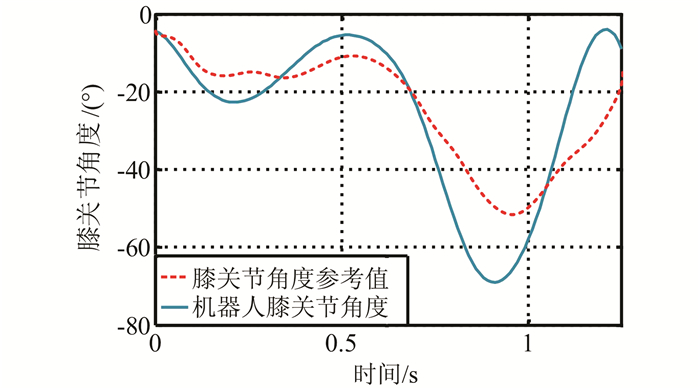
图 5为100代之后PSO所追踪的大腿处角度变化,图 6为膝盖处角度的变化.其中,蓝色实线为机器人的实验数据,红色虚线为被模仿者的行为数据.根据图 5和图 6,大腿角度均方根误差为7.71°,膝盖处角度均方根误差为21.34°.从图 5中可知在起步阶段大腿角度的误差追踪并不大,最大的均方根误差出现在临近摆动阶段结束的时候,即腿接触地面之前.
|
| 图 5 利用粒子群优化后的机器人大腿部位角度与实际参考值跟踪图 Figure 5 Figures of thigh angle tracking for both PSO simulation results and the able bodies reference data |
|
| 图 6 利用粒子群优化后的机器人膝关节部位角度与参考值对比 Figure 6 Figures of knee angle tracking of PSO simulation along with the able bodied reference data |
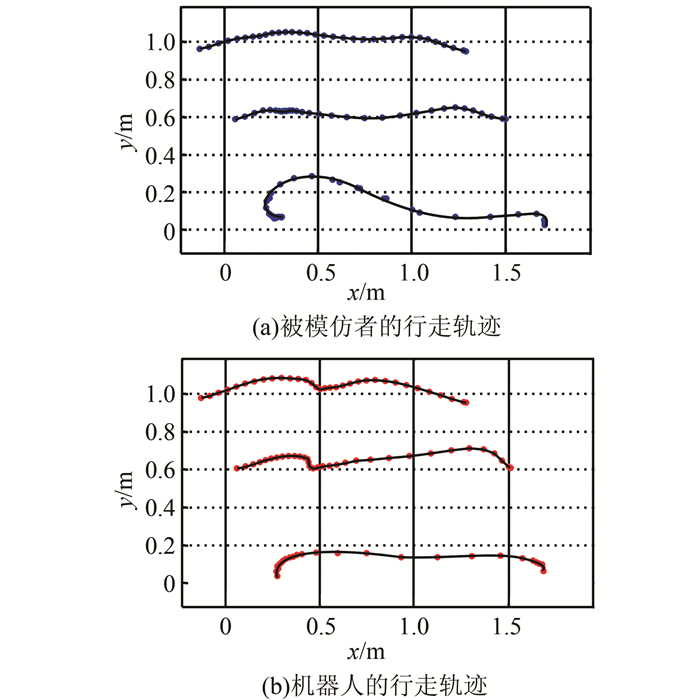
图 7展示了被模仿者和机器人的行走轨迹.其中,每幅图片中,上中下3条曲线分别表示臀部、膝部以及脚踝部位在一个行走循环中的轨迹.图 7(a)是体格健全的被模仿者的行走步态参考数据,图 7(b)是根据图 5和图 6的仿真模拟数据制成的模拟图.对比可见,人类脚部比机器人模拟脚部抬离地面更高,意味着机器人腿部无法形成过高的负角,这可以从图 6中膝盖角度参考数据看出.尽管膝盖角度跟踪并不非常接近,然而根据图 7中展示的行走动作可知,在起步阶段的初始时刻所成角度良好,当腿准备进入摆动阶段时,膝盖得到更饱满的伸张,和参考数据几乎达成一致.关于大腿部位,其关节最终成的角度极其接近膝盖的初始位置,这样对于下一个步幅来说,整个大腿所处的状态是理想的.
|
| 图 7 被模仿者与机器人的行走轨迹 Figure 7 Tracking of walking trajectory for both reference data and robot data |
由于每个人走路时具有不同的特点与风格,就算是最完美的膝盖大腿角度捕捉也无法适用于两个体格健全的人.对于舞蹈机器人而言,尽管大腿膝盖处角度跟踪存在均方差误差,然而由于参考指标下的拟人行走动作完成并不存在较大影响,因此本文的优化策略具有一定的可行性.
3 总结与展望本文构建了舞蹈机器人行走的步态模型,通过模拟人类的步态数据,利用粒子群优化方法对构建机器人步态模型的参数进行设置,实现舞蹈机器人大腿与膝盖与被模仿者大腿与膝盖的追踪,最小化跟踪误差.根据优化结果,舞蹈机器人能够较好地完成行走步态,完成拟人化的优化目标.
在下一步的工作中,将围绕多目标优化进行参数优化,对臀部角度以及膝部角度同时进行优化,并在优化过程中实施动态优化,将不同时段的优化结果反馈于下一时刻的步态控制,从而在舞蹈机器人臀部和膝部进一步提高优化精度.此外,还将考虑舞蹈机器人跳跃、转向等更加复杂的动作.
| [1] |
李建, 陈卫东, 王丽军, 等. 不平整地面上双足机器人的步态控制[J].
东南大学学报(自然科学版), 2009(S1): 129–133.
Li Jian, Chen Weidong, Wang Lijun, et al. Walking control for biped robots on unevenground[J]. Journal of Southeast University(Natural Science Edition), 2009(S1): 129–133. |
| [2] |
谭建豪, 章兢, 何志. 人类控制策略在双足机器人步态控制中的应用[J].
电子测量与仪器学报, 2013(1): 8–14.
Tan Jianhao, Zhang Jing, He Zhi. Application of human control strategy in the gait control of biped robot[J]. Journal of Electronic Measurement and Instrument, 2013(1): 8–14. |
| [3] |
王丽杨, 刘治, 曾小杰, 等. 基于能效优化的双足机器人步态控制方法[J].
控制理论与应用, 2011(5): 667–674.
Wang Liyang, Liu Zhi, Zeng Xiaojie, et al. Gait control based on energy-efficiency optimization for biped robots[J]. Control Theory & Applications, 2011(5): 667–674. |
| [4] |
王立鹏, 王军政, 汪首坤, 等. 基于足端轨迹规划算法的液压四足机器人步态控制策略[J].
机械工程学报, 2013(1): 39–44.
Wang Lipeng, Wang Junzheng, Wang Shoukun, et al. Strategy of foot trajectory generation for hydraulic quadruped robots gait planning[J]. Journal of Mechanical Engineering, 2013(1): 39–44. |
| [5] |
杨贵志, 马书根, 李斌, 等. 面对蛇形机器人的三维步态控制的层次化联结中枢模式生成器模型[J].
自动化学报, 2013(10): 1611–1622.
Yang Guizhi, Ma Shugen, Li Bin, et al. A hierarchical connectionist central pattern generator model for controlling three-dimensional gaits of snake-like robots[J]. Acta Automatica Sinica, 2013(10): 1611–1622. |
| [6] |
张国腾, 荣学文, 李贻斌, 等. 基于虚拟模型的四足机器人对角小跑步态控制方法[J].
机器人, 2016(1): 64–74.
Zhang Guoteng, Rong Xuewen, Li Yingbin, et al. Control of the quadrupedal trotting based on virtual model[J]. Robot, 2016(1): 64–74. |
| [7] |
蔡楷旋, 蔡勇, 杨益. 四足机器人柔性腿的步态运动图元分析[J].
械设计与制造, 2016(2): 232–235.
Cai Kaixuan, Cai Yong, Yang Yi. Analysis of gait motion primitives of aquadruped robot with a flexible leg[J]. Machinery Design & Manufacture, 2016(2): 232–235. |
| [8] |
丁加涛, 肖晓辉, 王杨. 足步行机器人在线步态生成与偏航控制策略[J].
中南大学学报(自然科学版), 2016(4): 1136–1143.
Ding Jiatao, Xiao Xiaohui, Wang Yang. Strategy for biped gait robot online generation and yaw control[J]. Journal of Central South University(Science and Technology), 2016(4): 1136–1143. |
| [9] |
李攀, 魏洪兴. 双足机器人步态规划方法研究[J].
机械工程与自动化, 2017(4): 22–24.
Li Pan, Wei Hongxing. Method of gait planning for biped robot[J]. Mechanical Engineering & Automation, 2017(4): 22–24. |
| [10] | Crispin Y. An evolutionary approach to nonlinear discrete-time optimal control with terminal constraints[C]// Informatics in Control, Automation and Robotics Ⅰ (Braz J, Vieira A, Encarnacao B, editors), Springer, 2006: 89-97. |
| [11] | Lee S, Fink W, von Allmen P, et al. Evolutionary computing for low-thrust navigation[C]// AIAA Space Conference, Long Beach, California, August 30 September 1, 2005. |
| [12] | Abo-Hammou Z, Yusuf M, Mirza N, et al. Numerical solution of second-order, two-point boundary value problems using continuous genetic algorithms[J]. International Journal for Numerical Methods in Engineering, 2004, 6: 1219–1242. |
| [13] | Yokose Y, Izumi T. Non-linear two-point boundary value problem obtaining the expansion coefficients by the dynamic GA and its application[J]. IEEE Transactions on Electronics, Information and Systems, 2005, 124: 2179–2186. |
| [14] | Farzadpour F, Danesh M, TorkLarki S M. Development of multi-phase dynamic equations for a seven-link biped robot with improved foot rotation in the double support phase[J]. Proceedings of the Institution of Mechanical Engineers Part C—Journal of Mechanical Engineering Science, 2015, 229: 3–17. |
| [15] | van den Bogert A, Samorezov S, Davis B, et al. Modeling and optimal control of an energy-storing prosthetic knee[J]. Journal of Biomechanical Engineering, 2012, 134: 1–8. |
| [16] | Kennedy J, Eberhart R. Particle swarm optimization[C]// Proceedings of IEEE International Conference on Neural Networks, 1995. |
 2018, Vol. 51
2018, Vol. 51



