文章信息
- 陆晨, 祝小青, 胡晓斌
- LU Chen, ZHU Xiaoqing, HU Xiaobin
- 往复荷载作用下框架-自复位墙结构滞回性能研究
- Hysteresis performance of framed self-centering wall structure subjected to cyclic loading
- 武汉大学学报(工学版), 2019, 52(6): 497-503
- Engineering Journal of Wuhan University, 2019, 52(6): 497-503
- http://dx.doi.org/10.14188/j.1671-8844.2019-06-004
-
文章历史
- 收稿日期: 2018-06-01
随着社会经济水平的快速发展,抗震结构不仅要保证大震不倒,而且还需要在震后可以迅速地恢复正常使用,由此产生了自复位结构.自复位结构是指在震后基本不产生残余位移,不需或经少量的维修即可恢复正常使用的结构[1-4],该结构近年来得到了地震工程界的广泛关注.
作为一种典型的自复位结构,自复位墙结构在墙底设置水平缝和耗能的阻尼器,同时引入预应力筋增强自复位能力.自复位墙可与框架结构结合形成框架-自复位墙结构,近年来少数学者对其力学或抗震性能进行了研究.Ajrab等[5]通过非线性时程分析研究了6层框架-自复位墙结构的抗震性能,结果表明,安装阻尼器可使层间位移大大减少,甚至出现几乎无损伤的理想状态.Zibaei等[6]对10层和20层的框架-剪力墙结构、框架-自复位墙结构和纯框架结构,分别采用OpenSees进行了推覆分析,结果表明框架-自复位墙结构的变形介于框架结构与框架-剪力墙结构的变形之间,且其层间位移角和塑性铰分布更加均匀,并且,安装阻尼器能进一步增强框架-自复位墙结构的延性和耗能能力.Wada等[7]通过非线性时程分析,研究了某框架结构在增设自复位墙、阻尼器以及预应力筋前后地震响应的变化,结果表明,结构在加固后可以按照预期的损伤模式发生破坏且地震响应显著减小.杨树标等[8]基于连续化假定和协同工作原理,建立了框架-自复位墙结构刚接和铰接体系的计算模型,求解了在不同侧向力作用下结构的位移和内力响应,结果表明,随着自复位墙抗弯刚度的增加,刚接体系的顶点位移逐渐减少而铰接体系的顶点位移不变.
综上可以看出,目前针对框架-自复位墙结构的研究主要采用了数值模拟的方法,少量的理论研究仅进行了线弹性分析,且没有考虑阻尼器和预应力筋的影响.基于此,本文采用理论分析方法,首先建立框架-自复位墙结构的简化计算模型,然后通过变参分析,研究预应力筋、阻尼器及框架各设计参数对其滞回性能影响.
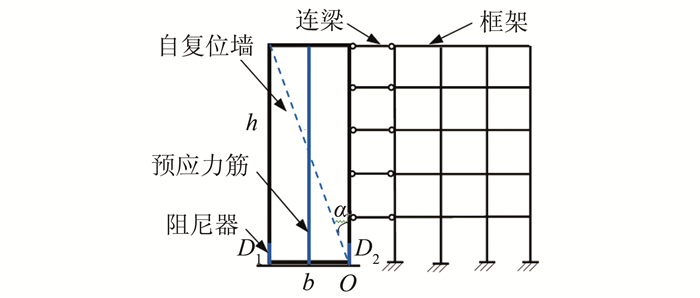
1 框架-自复位墙结构计算模型框架-自复位墙结构主要由自复位墙、连梁和框架3部分组成,如图 1所示,其中,b和h分别表示自复位墙的宽度和高度,α表示自复位墙对角线与竖直线的夹角.此外,假定阻尼器布置在墙底两端,如D1、D2所示;预应力筋布置在墙体中央.
|
| 图 1 框架-自复位墙结构简图 Fig. 1 Sketch of wall structure framed self-centering wall structure |
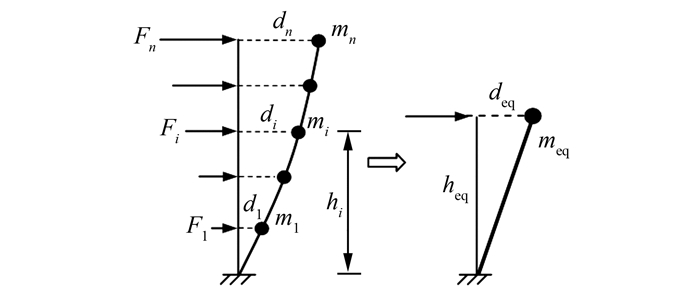
为简化计算,根据基于位移的抗震设计(DBSD)思路[9-11],可将框架-自复位墙结构中的框架部分等效为单质点体系,如图 2所示.等效单质点体系的参数计算公式如下:
|
| 图 2 等效单质点体系 Fig. 2 Equivalent single-degree-of-freedom system |
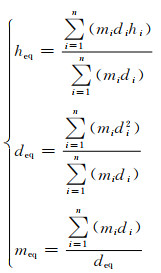 (1)
(1)
式中:heq、deq、meq分别表示等效体系的高度、水平位移及质量;hi、di、mi分别表示原框架第i层高度、水平位移及质量.
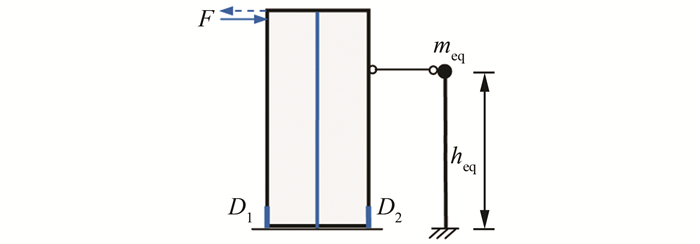
另外,将自复位墙部分简化成刚体,考虑连梁与自复位墙之间为铰接连接,可得框架-自复位墙的简化计算模型如图 3所示,设水平力F向右作用为正.
|
| 图 3 框架-自复位墙结构简化计算模型 Fig. 3 Simplified computational model of framed self-centering wall structure |
采用图 3所示计算模型,对框架-自复位墙结构进行水平荷载作用下的受力分析.设自复位墙的墙体自重为W,在正向水平荷载作用下绕O点转动,转角为θ,连梁的水平力为p,如图 4所示.设预应力筋的初始力Fp0,弹性刚度为kp,且预应力筋一直保持弹性状态.由图 4可知:
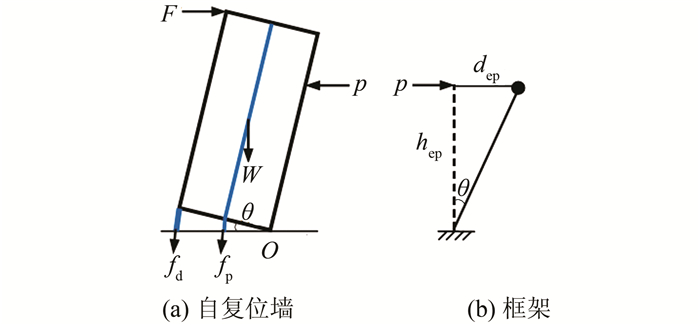
|
| 图 4 框架-自复位墙结构受力分析 Fig. 4 Mechanical analysis of framed self-centering wall structure |
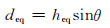 (2)
(2)
对于自复位墙部分(图 4(a)),对O点取矩,可得如下平衡方程:
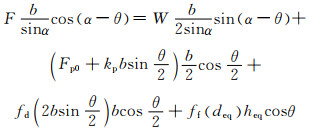 (3)
(3)
式中: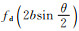
阻尼器及框架均考虑弹塑性,设其恢复力模型均为理想弹塑性模型,分别如图 5(a)、(b)所示.其中,Fd表示阻尼器的屈服力,kd表示阻尼器的弹性刚度,Ff表示框架的屈服力,kf表示框架的弹性刚度.
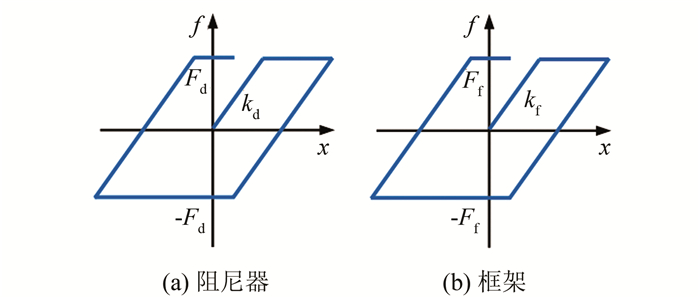
|
| 图 5 阻尼器及框架的恢复力模型 Fig. 5 Restoring force model of damper and frame |
为求得框架部分的弹性刚度与屈服力,可单独对框架进行推覆分析,得到基底剪力V-顶点位移dn曲线(见图 6(a)),然后利用式(1)将其转化成等效单质点体系的力-位移曲线(见图 6(b)),最后采用作图法确定等效体系的屈服点,即可确定Ff、kf.
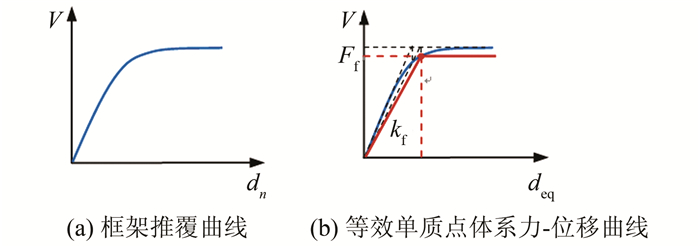
|
| 图 6 框架屈服力与弹性刚度的确定 Fig. 6 Determination of yield force and stiffness of frame |
式(2)、(3)构成了水平正向加载下框架-自复位墙结构的基本方程,结合图 5所示的恢复力模型,即可求得框架-自复位墙结构的水平力-转角滞回曲线.值得说明的是,反向加载下的分析过程与正向加载类似,且所得的滞回曲线和正向加载下的曲线基本对称,为节省篇幅,本文仅给出了正向加载下的情况.
3 框架-自复位墙结构典型的滞回曲线 3.1 特征点定义根据框架-自复位墙结构的受力特点,定义表 1所示的9个特征点.利用阻尼器和框架的恢复力模型(见图 5),根据几何关系,可得各特征点对应的转角,如表 1所示.值得注意的是,表中特征点的先后顺序跟参数取值有关,当参数取值变化时,其顺序可能发生变化.
| 点号 | 特征点状态 | 转角 |
| 1 | 墙体开始转动 | 0 |
| 2 | D1受拉屈服 | 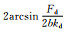 |
| 3 | 框架屈服 | 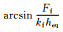 |
| 4 | 墙体开始卸载 | θ4 |
| 5 | D1卸载至0 | 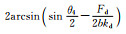
|
| 6 | D1受压屈服 | 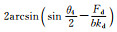
|
| 7 | 框架卸载至0 | 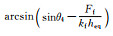
|
| 8 | 框架屈服 | 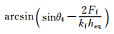
|
| 9 | 墙体复位 | 0 |
将各特征点的转角代入式(3),再利用阻尼器和框架的恢复力模型(见图 5),可求出各转角对应受到的水平力大小,于坐标系中绘出各点并按次序连接,即可得框架-自复位墙结构典型的滞回曲线,如图 7所示.可以看出,1号点和9号点均位于纵轴上.
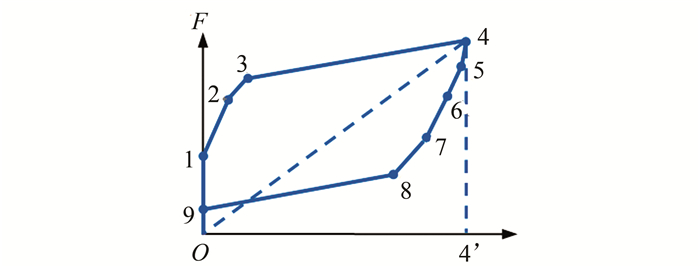
|
| 图 7 框架-自复位墙结构典型的滞回曲线 Fig. 7 Typical hysteresis curve of framed self-centering wall structure |
1号点为自复位墙开始转动的临界点,此时
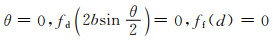 (4)
(4)
代入式(3),可得对应的水平力F1为
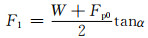 (5)
(5)
9号点表示墙体复位的特征点,此时
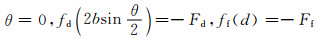 (6)
(6)
由式(6)可得对应的水平力F9为
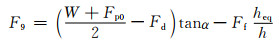 (7)
(7)
根据式(5)、(7)可以看出F1>F9,说明1号点的纵坐标总是大于9号点的纵坐标,满足构成滞回环的必要条件.
如框架-自复位墙结构没有残余位移,则9号点应位于横轴上方,此时F9≥0,由式(7)可得:
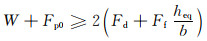 (8)
(8)
式(8)即为框架-自复位墙结构保证自复位性能应满足的必要条件.可以看出,当自复位墙的宽度以及框架的等效高度不变时,结构完全卸载时是否有残余位移与墙体自重、预应力筋初始力、阻尼器屈服力及框架屈服力的大小有关.
3.3 耗能能力耗能能力是表征结构抗震性能的重要指标[12].为了衡量框架-自复位墙结构的耗能能力,由图 7,定义等效粘滞阻尼比ζeq为
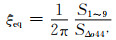 (9)
(9)
其中:S1~9代表 1~9点构成的滞回环的面积;SΔo44’代表O点、4点和4’点构成的三角形的面积.根据几何关系,进一步可得:
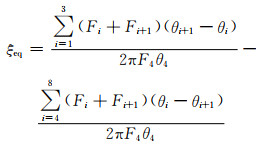 (10)
(10)
本节在前述基础上进一步研究预应力筋参数(包括初始力Fp0及弹性刚度kp)、阻尼器参数(包括屈服力Fd及弹性刚度kd)及框架参数(包括屈服力Ff及刚度kf)对框架-自复位墙结构滞回性能的影响.
设预应力筋、阻尼器及框架的设计参数基准值为:Fp0=1 532 kN,kp=79 kN/mm,Fd=10 kN,kd=6 kN/mm,Ff=500 kN,kf=15 kN/mm,然后在此基础上进行变化,各设计参数取值如表 2所示.
| 预应力筋 | 阻尼器 | 框架 | |||||
| Fp0/ kN |
kp/ (kN·mm-1) |
Fd/ kN |
kd/ (kN·mm-1) |
Ff/ kN |
kf/ (kN·mm-1) |
||
| 1 226 | 63 | 2 | 2 | 400 | 9 | ||
| 1 379 | 71 | 4 | 4 | 450 | 12 | ||
| 1 532 | 79 | 10 | 6 | 500 | 15 | ||
| 1 686 | 87 | 14 | 8 | 550 | 18 | ||
| 1 839 | 95 | 18 | 10 | 600 | 21 | ||
假定框架-自复位墙结构的墙体宽6 m,框架和墙的高度均为18 m,墙体自重W=622.08 kN,墙体卸载时的转角θ4为0.01,框架等效高度heq=12.8 m.
4.2 预应力筋设计参数的影响 4.2.1 预应力筋初始力为研究预应力筋初始力对框架-自复位墙结构滞回性能的影响,Fp0按表 2所示变化, 其余参数固定为基准值,计算所得F-θ曲线及ζeq如图 8所示.由图 8可以看出:1)当Fp0增大时,滞回曲线整体向上平移,形状基本保持不变;2)完全卸载后曲线在纵轴上的截距发生变化,表明结构是否有残余位移与Fp0有关;3)随着Fp0的增大,ζeq基本不变,表明结构的耗能能力与Fp0关系不大.
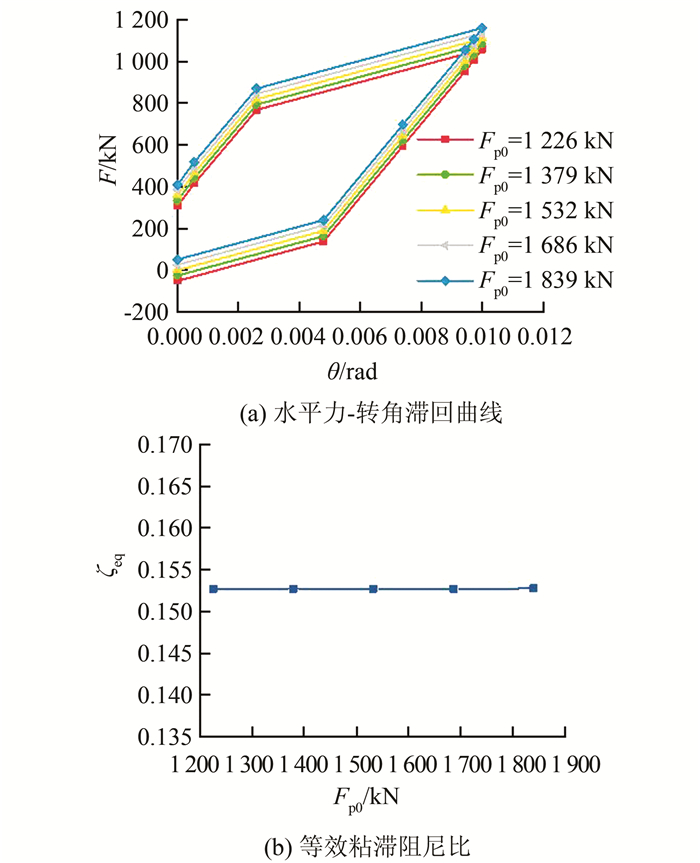
|
| 图 8 预应力筋初始力的影响 Fig. 8 Effect of initial load of prestressed tendon |
为研究预应力筋弹性刚度对结构滞回性能的影响,在其余参数固定为基准值的情况下,kp按表 2所示变化, 计算所得F-θ曲线及ζeq如图 9所示.由图 9可以看出:1)当kp增大时,滞回曲线的形状发生变化,其中4号点纵坐标的变化最大;2)完全卸载后结构是否有残余位移与kp无关;3)随着kp增大,ζeq减小,结构的耗能能力削弱.
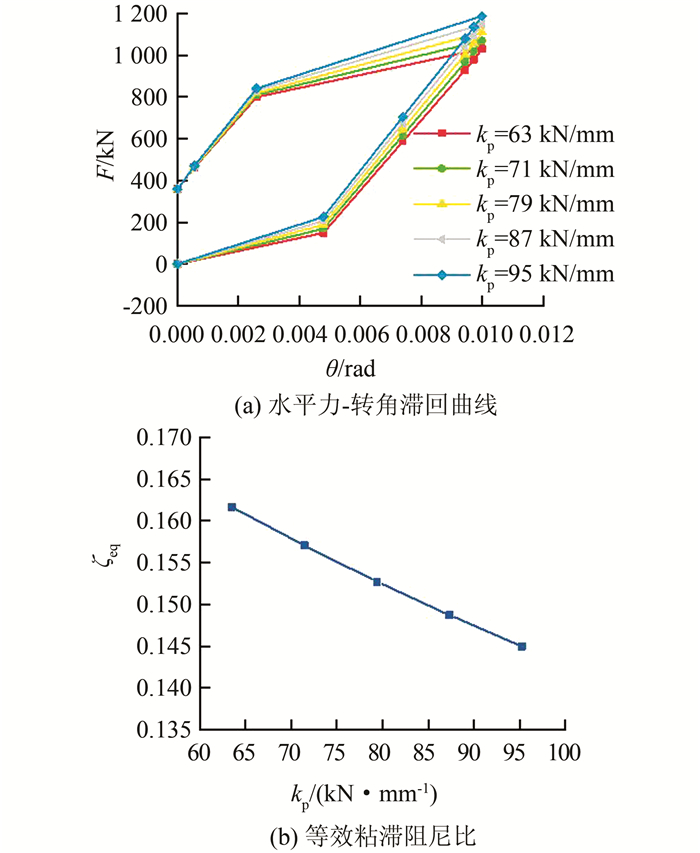
|
| 图 9 预应力筋弹性刚度的影响 Fig. 9 Effect of elastic stiffness of prestressed tendons |
为研究阻尼器屈服力对结构滞回性能的影响,在其余参数固定为基准值的情况下,Fd按表 2所示变化,绘出F-θ曲线及ζeq如图 10所示.由图 10可以看出:1)随着Fd的增大,滞回曲线的形状更加饱满;2)完全卸载后结构是否有残余位移与Fd无关;3)当Fd增大时,ζeq变大,结构的耗能能力增强.
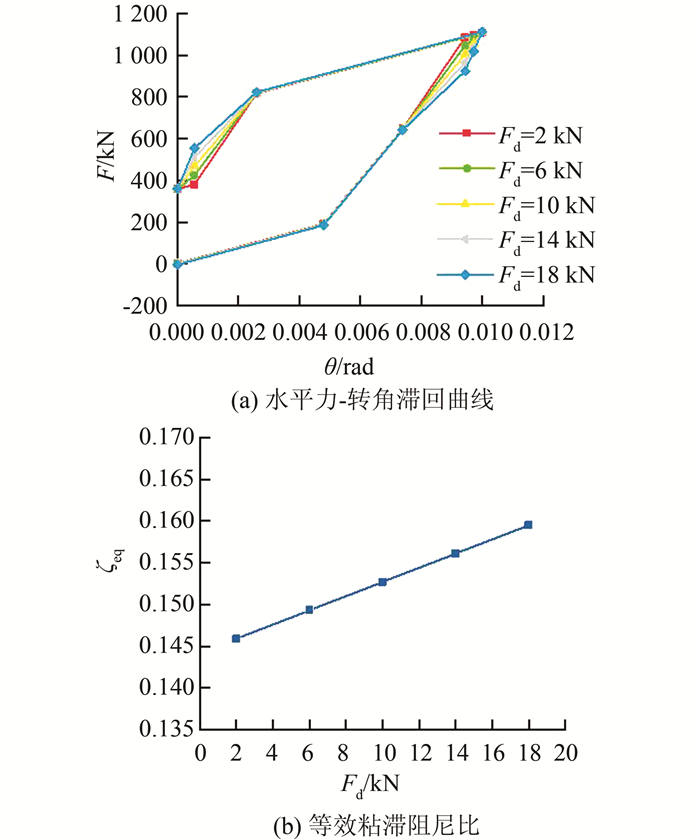
|
| 图 10 阻尼器屈服力的影响 Fig. 10 Effect of yield force of dampers |
为研究阻尼器弹性刚度对结构滞回性能的影响,在其余参数固定为基准值的情况下,kd按表 2所示变化,绘出F-θ曲线及ζeq如图 11所示.由图 11可以看出:1)当kd增大时,滞回曲线的形状趋于捏拢;2)完全卸载后结构是否有残余位移与kd无关;3)随着kd增大,ζeq减小,结构的耗能能力减弱.
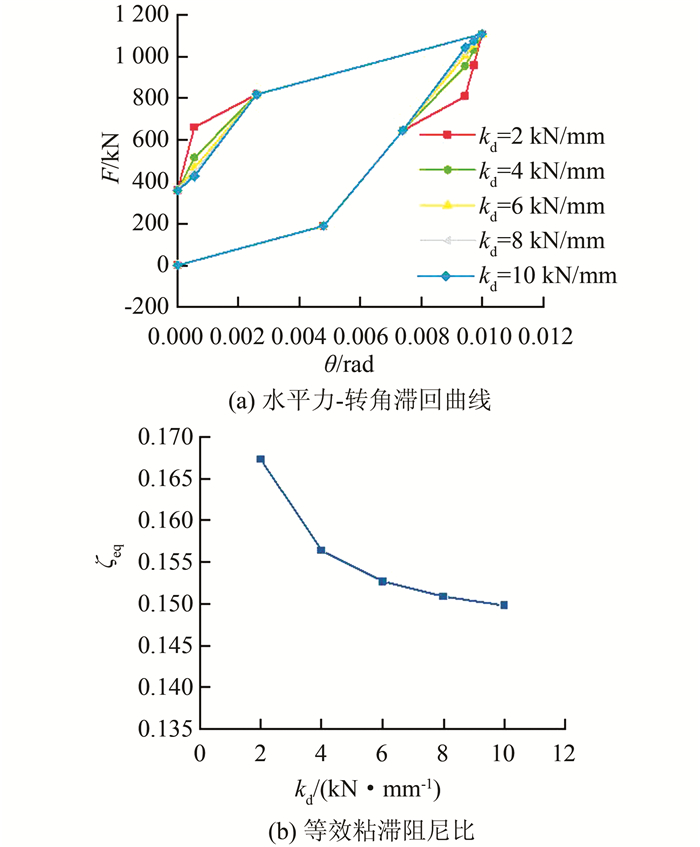
|
| 图 11 阻尼器弹性刚度的影响 Fig. 11 Effect of elastic stiffness of dampers |
为研究框架屈服力对结构滞回性能的影响,在其余参数固定为基准值的情况下,Ff按表 2所示变化,计算所得F-θ曲线及ζeq如图 12所示.由图 12可以看出:1)随着Ff的增大,滞回曲线的形状更为饱满;2)完全卸载后结构是否有残余位移与Ff有关;3)随着Ff的增大,ζeq显著增大,结构的耗能能力增强.
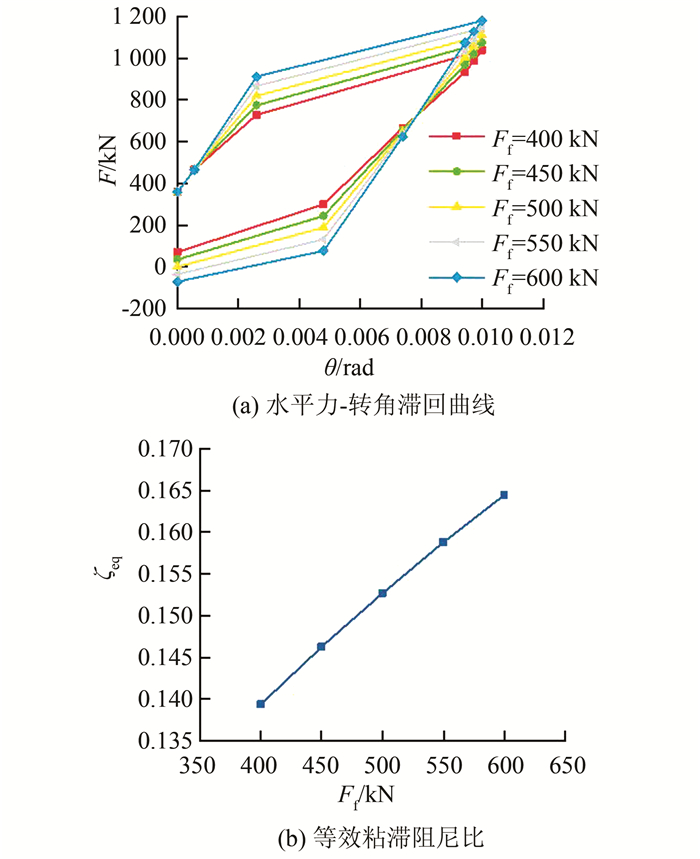
|
| 图 12 框架屈服力的影响 Fig. 12 Effect of yield force of frame |
为研究框架弹性刚度对结构滞回性能的影响,在其余参数固定为基准值的情况下,kf按表 2所示变化,计算所得F-θ曲线及ζeq如图 13所示.由图 13可以看出:1)当kf增大后,滞回曲线的形状趋于捏拢;2)完全卸载后结构是否有残余位移与kf无关;3)当kf增大时,ζeq逐渐减小,结构的耗能能力降低.
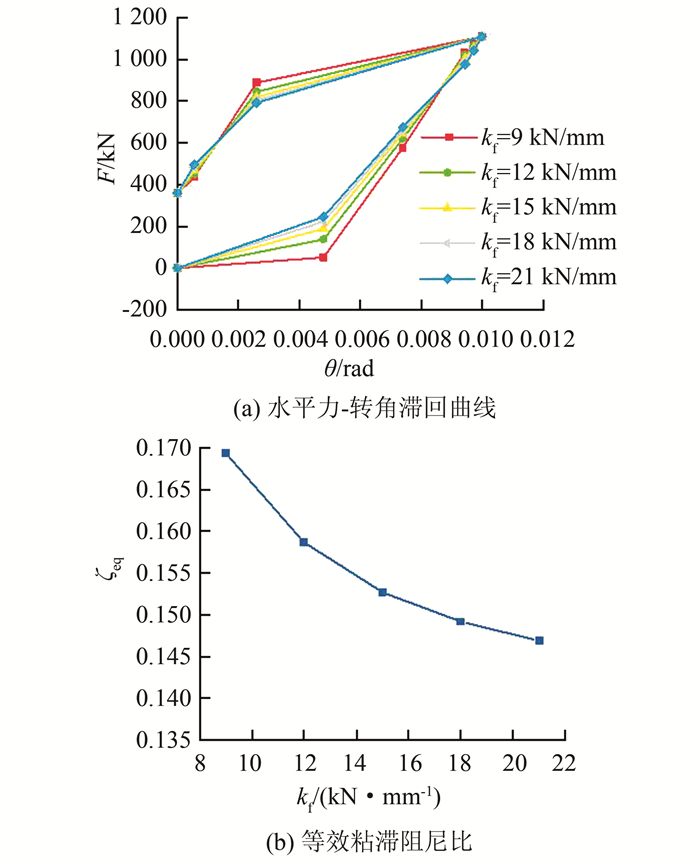
|
| 图 13 框架弹性刚度的影响 Fig. 13 Effect of elastic stiffness of frame |
本文首先建立了框架-自复位墙结构的简化计算模型,然后通过理论分析,研究了往复荷载作用下框架-自复位墙结构的滞回性能,分析了各设计参数对其滞回性能的影响,可以得出以下结论:
1) 当墙体的宽度以及框架的等效高度一定时,框架-自复位墙结构完全卸载后是否有残余位移与墙体自重、预应力筋初始力、阻尼器屈服力及框架屈服力的大小有关.
2) 提高阻尼器或框架的屈服力可以显著提高框架-自复位墙结构的耗能能力,提高预应力筋、阻尼器或框架的弹性刚度,均会降低其耗能能力.
3) 框架-自复位墙结构的耗能能力与预应力筋的初始力关系不大.
| [1] |
Seo C Y, Sause R. Ductility demands on self-centering systems under earthquake loading[J]. ACI Structural Journal, 2005, 102(2): 275-285. |
| [2] |
潘振华, 潘鹏, 邱法维, 等. 具有自复位能力的钢结构体系研究[J]. 土木工程学报, 2010, 43(增刊): 403-410. Pan Zhenhua, Pan Peng, Qiu Fawei, et al. Analysis of self-centering steel structures' development[J]. China Civil Engineering Journal, 2010, 43(Sup.): 403-410. |
| [3] |
周颖, 吕西林. 摇摆结构及自复位结构研究综述[J]. 建筑结构学报, 2011, 32(9): 1-10. Zhou Ying, Lü Xilin. State-of-the-art on rocking and self-centering structures[J]. Journal of Building Structures, 2011, 32(9): 1-10. |
| [4] |
江卫波, 胡晓斌, 郝彤. 强震下钢筋混凝土框架结构残余位移研究[J]. 武汉大学学报(工学版), 2017, 50(6): 842-849. Jiang Weibo, Hu Xiaobin, Hao Tong. Study of residual displacement of reinforced concrete frame structures under strong earthquake[J]. Engineering Journal of Wuhan University, 2017, 50(6): 842-849. |
| [5] |
Ajrab J J, Pekcan G, Mander J B. Rocking wall-frame structures with supplemental tendon systems[J]. Journal of Structural Engineering, 2004, 130(6): 895-903. DOI:10.1061/(ASCE)0733-9445(2004)130:6(895) |
| [6] |
Zibaei H, Mokari J. Evaluation of seismic behavior improvement in RC MRFs retrofitted by controlled rocking wall systems[J]. The Structural Design of Tall and Special Buildings, 2014, 23(13): 995-1006. DOI:10.1002/tal.1101 |
| [7] |
Wada A, Qu Z, Ito H, et al. Seismic retrofit using rocking walls and steel dampers[C]// Proceedings of the ATC&SEI Conference on Improving the Seismic Performance of Existing Buildings and Other Structures, San Francisco, United States, 2009.
|
| [8] |
杨树标, 余丁浩, 贾剑辉, 等. 框架-摇摆墙结构简化计算方法研究[J]. 工程抗震与加固改造, 2014, 36(2): 94-99. Yang Shubiao, Yu Dinghao, Jia Jianhui, et al. Simplified calculation method of frame rocking-wall structure system[J]. Earthquake Resistant Engineering and Retrofitting, 2014, 36(2): 94-99. DOI:10.3969/j.issn.1002-8412.2014.02.015 |
| [9] |
罗文斌, 钱稼茹. 钢筋混凝土框架基于位移的抗震设计[J]. 土木工程学报, 2003, 36(5): 22-29. Luo Wenbin, Qian Jiaru. Displacement-based seismic design for RC frames[J]. China Civil Engineering Journal, 2003, 36(5): 22-29. DOI:10.3321/j.issn:1000-131X.2003.05.005 |
| [10] |
梁兴文, 黄雅捷, 杨其伟. 钢筋混凝土框架结构基于位移的抗震设计方法研究[J]. 土木工程学报, 2005, 38(9): 53-60. Liang Xingwen, Huang Yajie, Yang Qiwei. Displacement-based seismic design method of RC frames[J]. China Civil Engineering Journal, 2005, 38(9): 53-60. DOI:10.3321/j.issn:1000-131X.2005.09.009 |
| [11] |
钱稼茹, 罗文斌. 建筑结构基于位移的抗震设计[J]. 建筑结构, 2001, 31(4): 3-6. Qian Jiaru, Luo Wenbin. Displacement-based seismic design for building structures[J]. Building Structures, 2001, 31(4): 3-6. |
| [12] |
宋子文.自复位耗能支撑结构的地震响应分析[D].哈尔滨: 哈尔滨工业大学, 2010. Song Ziwen. Seismic responses analysis of structures with self-centering energy dissipative braces[D]. Harbin: Harbin Institute of Technology, 2010. |
 2019, Vol. 52
2019, Vol. 52




