文章信息
- 崔溦, 李永杰, 戚蓝, 黄小龙, 刘灿平, 党彦
- CUI Wei, LI Yongjie, QI Lan, HUANG Xiaolong, LIU Canping, DANG Yan
- 高自生热材料注浆过程多场耦合数值分析
- Numerical analysis of multifield coupling in high self heating material grouting process
- 武汉大学学报(工学版), 2018, 51(11): 941-949
- Engineering Journal of Wuhan University, 2018, 51(11): 941-949
- http://dx.doi.org/10.14188/j.1671-8844.2018-11-001
-
文章历史
- 收稿日期: 2017-12-21
2. 内蒙古路桥集团有限责任公司,内蒙古 呼和浩特 010051
2. Inner Mongolia Road and Bridge Group Co., Ltd., Hohhot 010051, China
注浆是使用加压设备将能够固化胶结的浆液通过注浆孔注入到地层中的孔隙和裂隙之内,浆液固化后形成具有一定强度的结石体,能够满足相应工程的需要.注浆工程具有隐蔽性,注浆对象即地质条件的不确定性和浆液固化过程涉及流变和时变性,给注浆数值模拟研究带来了一定困难.尤其是对于高自生热材料,注浆过程涉及浆液渗流、岩体变形和温度效应,因此,热流固三场耦合是数值模拟中必须考虑的重要问题.
目前在煤气开采、地热开采、核燃料工程等领域对于热流固多物理场的研究较为广泛.盛金昌等[1]分析了钻井过程中温度骤降,井壁围岩的温度、应力等指标的变化;赵延林等[2]对高温岩体地热开发系统中的热流固耦合进行了数值模拟;Liu Quansheng等[3]对高放射性核废料地质处置系统围岩中热-水-力耦合过程进行了数值模拟.
注浆过程的流固耦合分析已有较多论文发表.张庆松等[4]分析了浆液与土体的界面应力耦合效应对土体劈裂注浆过程的影响;郑卓等[5]建立了考虑浆液对岩体单向耦合作用的裂隙岩体注浆理论模型,对注浆过程中浆液与围岩的相互作用展开了研究;张云龙等[6]基于流固耦合理论,分析了围岩后注浆对大型水封石油洞库水封性的影响;雷进生等[7]应用精细化的流固耦合力学模型,考虑物性参数变化和注浆时变效应,进行了注浆扩散模拟.已有的注浆模拟主要针对传统水泥基灌浆材料,由于生热量较为有限,温度影响一般都不予考虑.但是,高自生热材料的温度场除了会以荷载形式施加到岩体上,还会影响材料自身物理力学特性,其对流、固场的偶联效应不容忽视.
聚氨酯是一种可灌性较好的高分子注浆材料,根据石明生等[8, 9]的研究,聚氨酯在固化过程中化学反应强烈,反应速度较快,同时会释放大量的热量,产生持续的温度变化.本文以聚氨酯为研究对象,考虑热流固的偶联作用和材料属性的时变特性,研究了其在存在裂隙的多孔介质岩体中的注浆特性.
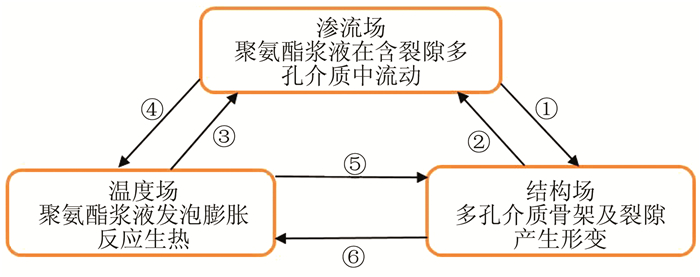
1 注浆过程热流固耦合机理热流固耦合作用指在注浆过程中涉及的孔隙和裂隙介质中最常见的渗流场、结构场和温度场之间直接或间接的相互作用,其真实地反映了孔隙、裂隙介质在多物理场复杂条件下的物理行为[10].注浆过程热流固耦合机理见图 1.
|
| 图 1 热流固耦合机理分析图 Fig. 1 Schematic diagram coupled thermal-hydrological- mechanical proces |
① 浆液的渗透流动现象是由于渗流区域周边边界的总水头与注浆孔处的总水头存在一定的压力差而引起的.在注浆过程中,由于注浆孔处的压力水头较大,距注浆孔一定距离处或边界处的压力水头相对较小,注浆行为使多孔介质域中产生压力差,从而促使浆液在含裂隙多孔介质中产生渗流运动.浆液在渗流运动过程中,产生渗流动水压力,渗流动水压力以渗流体积力和渗流表面力的形式作用于孔隙介质及裂隙通道表面.渗流力可以视为外部荷载,使得多孔介质域应力场发生变化,进而位移场改变,从而使含裂隙多孔介质形成形变,这即是渗流场对结构场(应力场、应变场、位移场)的影响.
② 多孔介质产生形变后其孔隙率发生改变,使得流体的渗流通道发生改变,渗流通道的改变引起注浆对象渗透率的改变[11].渗透率改变势必影响渗流场的分布,结构场对渗流场的影响一般通过渗透系数和储水系数来表征.
③ 在注浆过程中,由于浆材在固化过程中同时伴有化学加聚反应,会释放大量的热量,使得浆液温度发生变化,浆液的密度、粘度均与温度有关.浆液密度及粘度的变化造成渗透系数改变,间接影响浆液在多孔介质中的流动.
④ 在流动过程中,浆液与含裂隙多孔介质产生热量传递,其传递形式为热传导,从而产生温度势梯度.由于温度势梯度的存在,促使浆液体从温度较高的区域流向温度相对较低的区域,进而使得浆液运动发生改变,并伴有热对流产生.由于多孔介质中渗流场的存在与改变,使渗透浆液参与多孔介质系统的热量交换与传递.
⑤ 温度场对结构场的影响主要表现为多孔介质域内温度的变化,从而影响多孔介质固有的物理力学性质[12],例如当多孔介质温度升高,导致弹性模量、泊松比及强度变化.同时温度效应产生热应力和热应变,引起岩体裂隙张闭、变形,从而位移场随之变化.
⑥ 结构场对温度场的影响表现为应力场的改变能够引起多孔介质结构改变,从而产生力学能量转换,引起导热系数等一系列热力学参数发生变化,使温度场产生相应的重分布.
2 注浆过程热流固全耦合数学模型注浆过程中的假设如下:①浆液在孔隙介质和裂隙介质中的流动符合改进的达西定律;②由于浆液自生热,认为浆液的热传导系数远大于多孔介质骨架;③裂隙中不考虑毛管力;④含裂隙多孔介质本构关系的建立基于线性热弹性假设.
2.1 渗流场控制方程渗流控制方程是将流体连续性方程、状态方程、达西定律结合起来,消去某些量推导出的联系应变、水压力与温度的偏微分方程[10, 13]:
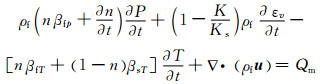 (1)
(1)
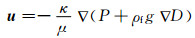 (2)
(2)
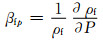 (3)
(3)
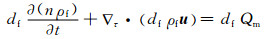 (4)
(4)
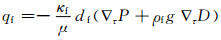 (5)
(5)
式中:ρf为流体密度;n为孔隙率;μ为浆液粘度;βfp为流体的压缩系数;P为流体压力;εv为多孔介质域体积应变;βfT为流体热膨胀系数;βsT为多孔介质热膨胀系数;T为流体温度;u为流速矢量;▽和▽τ为密哈顿算子;df为裂隙的开度;κ和κf分别为多孔介质和裂隙的渗透率张量;▽D为重力作用方向上的单位矢量;K为排水体积模量;Ks为固体骨架体积模量;t为时间变量; qf为单位长度裂隙体积流量.
方程(1)即为热流固全耦合模型中的渗流场控制方程;方程(2)、(5)分别为孔隙介质和裂隙介质中改进的达西渗流方程;方程(3)为流体压缩系数方程;方程(4)、(5)分别为裂隙中流体质量守恒方程和运动方程.
2.2 结构场控制方程多孔介质本构关系基于线性热弹性假设,即材料的总应变为应力引起的应变、水压力导致的应变与热应变之和.由平衡方程、达西方程、应力应变关系可得热流固耦合应力控制方程[10, 14-17]:
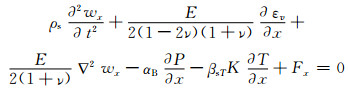 (6)
(6)
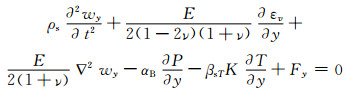 (7)
(7)
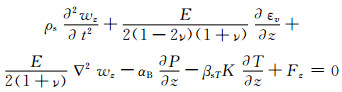 (8)
(8)
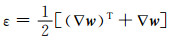 (9)
(9)
式中:ρs为多孔介质的密度;w为位移矢量;wx、wy、wz分别为x、y、z方向位移分量;Fx、Fy、Fz分别为x、y、z方向体积力分量;E为弹性模量;t为时间变量;ν为泊松比;εv为体积应变;P为水压力;βsT为多孔介质热膨胀系数;K为排水体积模量;T为多孔介质体温度;ε为应变张量;αB为比奥系数.
方程(6)、(7)、(8)分别为x、y、z方向的应力控制方程, 方程(9)为几何方程.
2.3 温度场控制方程固体骨架和流体存在于同一个体积空间,但它们具有不同的热力学特性,如比热容和热传导系数,因此,应对多孔介质体和流体分别定义能量方程,但对于单向流,假设固体和流体总是处于热平衡状态,因此可以叠加,并考虑变形能,即可得到能量方程[14-18]:
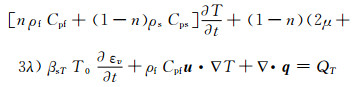 (10)
(10)
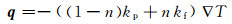 (11)
(11)
式中:n为孔隙率; ρf为流体密度;Cpf为流体热容;Cps为多孔介质热容;ρs为多孔介质密度;μ、λ为拉梅常数;T0为无应力状态绝对温度;βsT为多孔介质热膨胀系数;εv为体积应变;u为流体流速场;q为热通量;kp、kf分别为多孔介质和流体导热系数.
将方程(11)即傅里叶导热定律,代入方程(10)即可得温度场控制方程.
2.4 动态参数耦合方程聚氨酯浆液在注浆过程中,浆液自身固化放热,注浆压力和温度作用使聚氨酯浆液密度动态改变,可以表示为
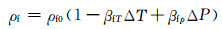 (12)
(12)
式中:ρf0为初始聚氨酯浆液密度;βfT、βfp分别为聚氨酯浆液的热膨胀系数和压缩系数.
对于非固结颗粒多孔介质而言,初始渗透率和初始孔隙率及颗粒直径有密切联系,根据文献[18],初始渗透率如下:
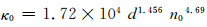 (13)
(13)
式中:n0为初始孔隙率;κ0为初始渗透率, μm2;d为颗粒平均直径,mm.
在注浆过程中,多孔介质内流体的孔隙压力变化会同步引起骨架有效应力的变化,进而影响多孔介质的物性参数变化[18, 19].由于应力场的变化,导致多孔介质体产生形变,必然对多孔介质的渗透性产生影响,孔隙的大小对多孔介质体的渗透性起主导作用[7].多孔介质渗透率和孔隙率模型如下:
 (14)
(14)
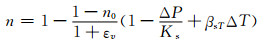 (15)
(15)
式中:n0、κ0分别为初始孔隙率和初始渗透率;εv为体应变;ΔP=P-P0, P0为初始孔隙水压力;ΔT=T-T0, T0为无应力状态绝对温度;Ks为多孔介质体积模量;βsT为多孔介质热膨胀系数.
在注浆过程中,多孔介质结构发生改变,使得多孔介质的力学参数发生变化,对计算结果会产生一定的影响.弹性模量的取值与动态孔隙率直接相关,文献[19]通过大量实验数据,采用高斯指数模型拟合弹性模量E、排水体积模量K、剪切模量G与动态孔隙率的关系:
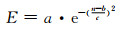 (16)
(16)
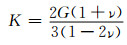 (17)
(17)
式中:a、b、c为常值,a=35.50, b=0.057 78, c=0.355 4;G=E/[2(1+ν)].
聚氨酯浆材注入饱和含水层多孔介质中,进入粘度无增加,并保持良好渗透性的一次渗透阶段.浆液与地下水接触后,存在一定的诱导期,此时粘度无增加,仍保持良好的渗透性.经过诱导期后开始加聚反应,产生二氧化碳气体,由于加聚反应发泡膨胀产生气体,使得介质内部渗透压力扩大,进而进入2次渗透阶段,此时浆液粘度迅速增加[12].根据石明生等[8, 9]对聚氨酯高聚物注浆固化温度试验,高聚物固化过程温度变化大致经历3个阶段,即升温段、恒温段、降温段,升温段历时3.18~5.68 min,恒温段和降温段时间维持稍长.由于本文的数学模型渗流场采用达西定律,因此选取整个升温段和恒温段初期为研究时间段.综上,拟取注浆压力函数如下:
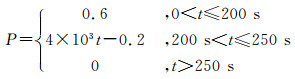 (18)
(18)
温度变化如下:
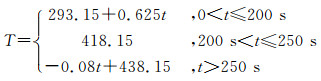 (19)
(19)
式(18)、(19)中:P为注浆压力,MPa; T为注浆过程中浆液温度; t为注浆时间.
聚氨酯浆液在流动和固化生热过程中粘度会产生变化.根据文献[20],浆液温度升高流体粘度降低,但温度升高化学反应速率加快,化学反应会对浆液粘度具有主导性影响.聚氨酯浆液的粘度变化满足如下关系:
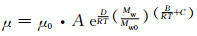 (20)
(20)
式中:μ0为初始粘度; Mw0为反应体系初始重均分子量;R为气体常数;Mw为重均分子量与反应程度的关系,见文献[20];T为温度;A、B、C、D为常数,其中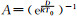
以COMSOL Multiphysics专业多场耦合软件为工具,将上文给出的注浆过程热流固耦合数学模型转化成统一的偏微分方程,在人机交互的环境下,一次解出渗流场、结构场和温度场,实现了热流固3场全耦合数值求解,避免了松散耦合法求解多场耦合问题带来的误差.
采用二维单孔注浆几何模型,模拟理想状态下注浆过程.多孔介质计算域为边长10 m的正方形,几何模型中心坐标为(0, 0),同时为注浆孔中心,注浆孔半径为0.1 m,注浆孔周围分布4条与坐标轴平行的主裂隙,长度1.3 m,主裂隙末端分成2条次级裂隙,长度为0.632 m,夹角为36.87°,4条主裂隙呈中心对称分布.
边界条件:注浆孔为压力边界和温度荷载边界;四周为无流动、无位移且热绝缘边界;主、次裂隙分别为不同开度的渗流和传热裂隙边界.
计算参数及初始条件:注浆过程时间为250 s,本文研究属低压静态注浆,静水压力为0.05 MPa.注浆压力为分段函数,见式(18).注浆压力施加主要分为2个阶段,第1阶段为恒压注浆,P为0.6 MPa;随着注浆行为的持续,聚氨酯浆液发泡膨胀, 进入2次渗透阶段, 即第2阶段,注浆压力为时间函数,其最大值为0.8 MPa.
为构建注浆对象的非均质性,采用以横纵坐标为变元、孔隙率平均值为0.4、标准偏差为0.01符合正态分布的函数构建随机初始孔隙率.注浆模型初始孔隙率及网格见图 2.
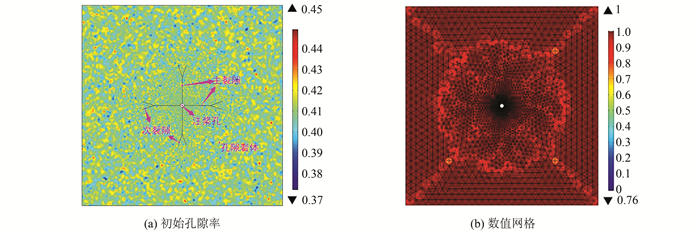
|
| 图 2 注浆数值模型(单位:MPa) Fig. 2 Initial porosity and mesh quality of grouting model (unit:MPa) |
根据相关文献研究,亚洲大陆常温带地表常年平均温度为15 K,地层温度梯度变化为每100 m温度升高3 K[21],本文研究浅地层注浆模拟,距地面深度较浅,地层温度梯度影响较小,因此,多孔介质域初始地温拟为常数288.15 K.聚氨酯浆液初始密度为1.088 g/cm3,固化度峰值为418.15 K[8].聚氨酯浆材属于二液型化学灌浆材料,通过注浆设备注入含裂隙多孔介质,浆液2次渗透前,浆液粘度无增加,并且保持良好的渗透性[12].选取较低粘度品级浆材,在常温下稀释后粘度为10.5 mPa·s,即为初始粘度.计算参数详见表 1.
| 渗透力学参数 | 初始浆液密度ρf0/(kg·m-3) | 1 108 |
| 裂隙孔隙率nc | 0.9 | |
| 浆液初始粘度μ0/(mPa·s) | 10.5 | |
| 静水压力P0/MPa | 0.05 | |
| 骨架平均颗粒直径d/mm | 0.01 | |
| 比奥系数αB | 1 | |
| 固体力学参数 | 多孔介质密度ρs/(kg·m-3) | 2 600 |
| 有效体积模量Ks/Pa | 1×1011 | |
| 泊松比ν | 0.25 | |
| 热力学参数 | 初始温度T0/K | 288.15 |
| 多孔介质比热容Cps/(J·kg-1·K-1) | 837 | |
| 多孔介质导热系数kp/(W·m-1·K-1) | 3.08 | |
| 介质热膨胀系数βsT/K-1 | 0.8×10-5 | |
| 浆液热膨胀系数βfT/K-1 | 2.17×10-4 | |
| 浆液重均分子量Mw0 | 706 | |
| 气体常数R | 8.314 | |
| 常数B/(J·mol-1) | 20.96×103 | |
| 常数C | 5.23 | |
| 常数D/(J·mol-1) | 54.041×103 |
为了分析3场耦合效应对注浆过程的影响,本文数值模拟共分析了4种工况.工况1:只针对浆液在孔隙和裂隙中渗流过程进行数值模拟,即非耦合工况(H工况);工况2:考虑浆液渗流的同时,考虑浆液渗流体积力作用于多孔介质、多孔介质与浆液渗流的互馈效应,即流固耦合工况(HM工况);工况3:在工况2的基础上考虑浆液迁移过程中浆液自身生热效应对渗流场和结构场机制的影响,即热流固耦合工况(THM1工况);工况4:在工况3的基础上,考虑浆液迁移过程中发泡膨胀2次渗透浆液粘度速增(THM2工况).
1) 注浆过程中,浆液受注浆压力作用,被压入与注浆孔接触的孔隙介质和裂隙通道.当注浆时间为10 s时,注浆孔右侧主裂隙开度分别为0.001、0.01、0.05、0.1、0.5、1 mm,其他裂隙开度为0时,HM工况注浆压力扩散如图 3所示.由图 3分析可知,注浆压力在孔隙介质中类似圆形扩散,在沿裂隙通道方向浆液呈现彗星状扩散形态.从图中还可以看出裂隙通道中浆液从裂隙介质向孔隙介质扩散时的注浆压力梯度分布:距注浆孔壁越远,浆液渗透压力沿裂隙通道法向扩散距离越小.裂隙开度越大,浆液扩散越迅速.裂隙开度为0.001 mm时,注浆压力扩散云图为近似同心圆形,此时裂隙介质与孔隙介质相比,注浆压力沿裂隙扩散占优效果并不明显,说明当裂隙开度降低到某一值时,裂隙扩散将等效为孔隙介质扩散.该定值即为孔隙介质渗流通道的等效几何尺度,该方法可以间接判断孔隙介质渗流通道等效几何尺度.本文计算案例所使用计算参数情况下,对应的孔隙介质微渗流通道宽度的几何尺度数量级为0.001 mm.
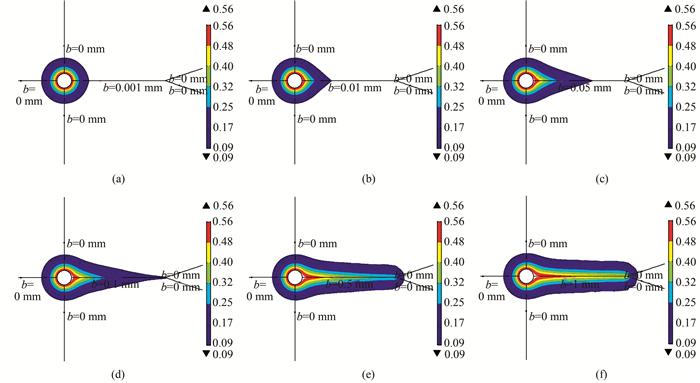
|
| 图 3 不同裂隙开度注浆压力扩散图(单位:MPa) Fig. 3 Pressure diffusion map of different crack widths (unit:MPa) |
2) 图 4给出了在THM2工况下,注浆孔左侧和下侧主、次裂隙开度分别为0.1和0.05 mm,注浆孔右侧、上侧主、次裂隙的开度分别为0.5和0.25 mm, 在注浆50、100、160、250 s时刻温度扩散等值线图.由图 4分析可得,孔隙介质与裂隙介质相比,浆液优先在裂隙中产生热对流,并且主裂隙中的热对流强度大于次裂隙中的对流强度;裂隙开度不同的裂隙介质相比,浆液在开度较大的裂隙通道中温度扩散速度较快.主裂隙通道法向距离裂隙通道一定距离处的不同时刻温度分布见图 5.由图 5可知,温度分布与时间呈正相关关系,注浆时间的延长,注浆总量越多,产生的热量越多,温度也必然会升高.温度与通道法向距离呈负相关关系,温度改变速率与裂隙法向距离同样呈现负相关关系.注浆时间越长,温度的扩散范围越大,注浆完成时温度扩散范围为0.33 m.由于浆液自生热产生的热量而引起的温度扩散范围有限.

|
| 图 4 温度等值线图(单位:K) Fig. 4 Temperature contour maps (unit:K) |
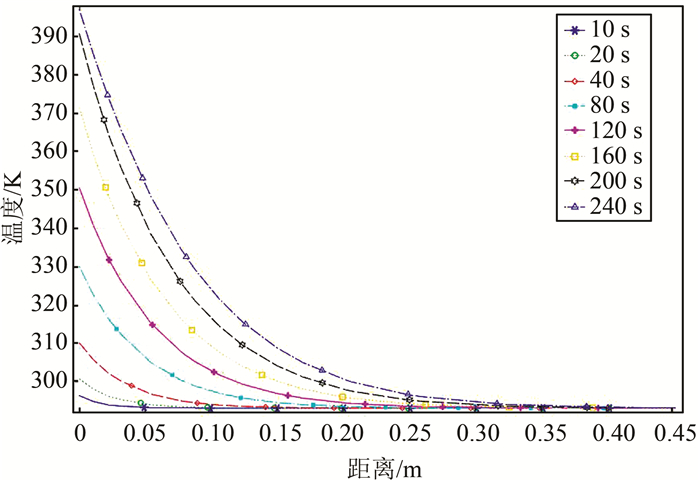
|
| 图 5 THM2工况下裂隙通道法向温度分布图 Fig. 5 Normal temperature distribution of fracture channel |
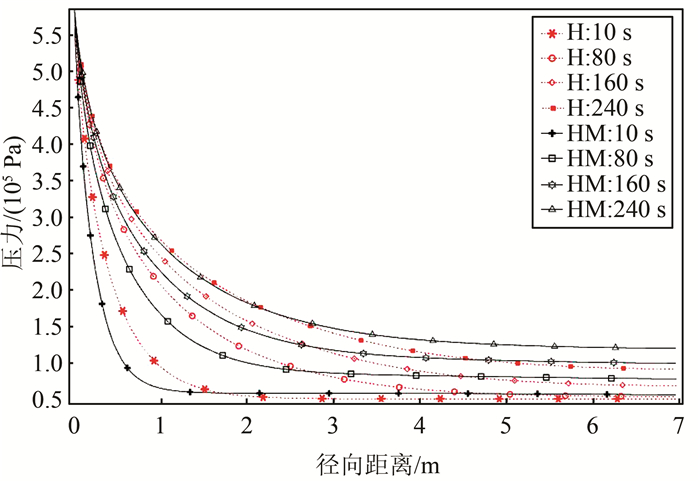
3) 图 6给出了在H和HM工况下,不同注浆时刻注浆孔径向孔隙介质渗透压力分布图.由渗透压力趋势图可知,2种工况压力分布规律一致,近注浆孔大,远离变小,符合压力消减一般规律;随着注浆时间增加,压力增加且逐渐向远端扩散,符合注浆过程压力变化规律;近注浆孔,HM工况下压力小于H工况,说明考虑流固耦合下孔隙发生变形引起压力消减,远离注浆孔,HM工况下压力大于H工况,说明考虑流固耦合下注浆压力导致孔隙变形胀开,从而使得浆液更易于在孔隙扩散.总体来看,考虑流固耦合的数值模拟更能反映实际注浆过程.
|
| 图 6 不同时刻注浆孔径向孔压分布图 Fig. 6 Pore size distribution of grouting pore at different times |
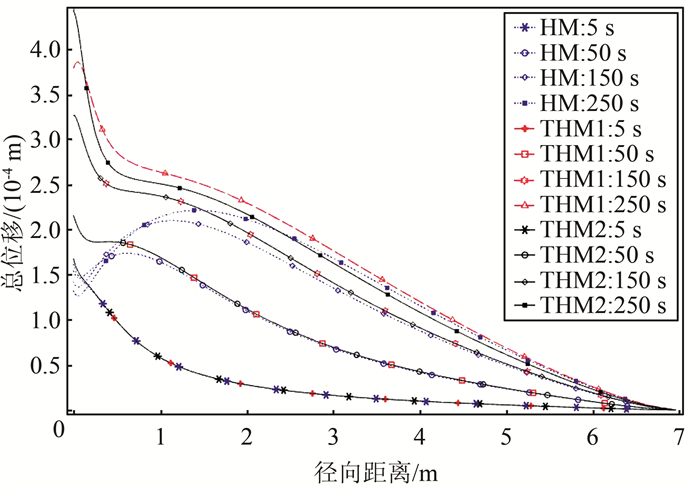
4) 图 7为注浆过程中HM、THM1、THM2三种耦合工况下不同时刻孔隙介质骨架变形情况.注浆过程中多孔介质骨架位移与径向距离总体呈负相关关系,位移随注浆时间延长而增大;5、50 s时3种耦合工况位移线图基本重合,说明注浆前期在孔隙介质中浆液的热效应可以忽略,150、250 s时, HM工况与THM1、THM2工况相比,距离注浆孔越近,孔隙介质骨架位移差别越大,说明热效应在距离注浆孔较近时更为明显;250 s时THM1和THM2工况骨架位移差别较大,说明浆液粘度变化是热流固耦合效应的主导因素.综上,注浆过程浆液自生热温度场对注浆过程有一定的影响,但主要表现为浆液流动特性影响,而温度扩散范围则较为有限.
|
| 图 7 不同时刻径向位移变化 Fig. 7 Radial displacement variation at different times |
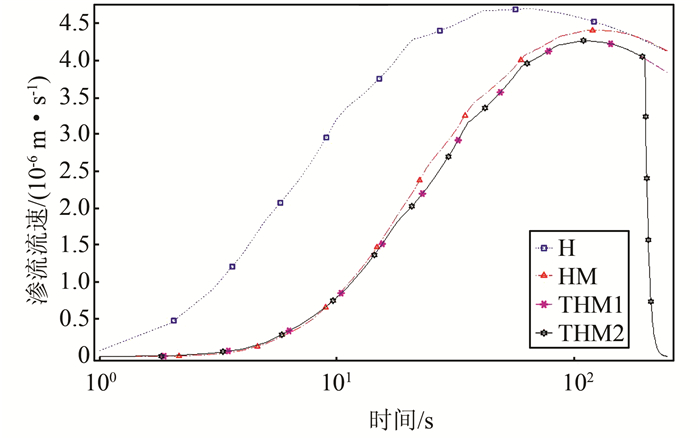
5) 图 8为孔隙介质中点(1,0.6)在4种工况下渗流流速随时间的变化图.由图 8可知在注浆行为持续100 s前,浆液渗流流速与注浆时间呈正相关关系,而渗流速度变化率与注浆时间为负相关关系,100 s后浆液渗流流速与注浆时间呈负相关关系,因为注浆前期为恒压注浆,浆液的注入总量随注浆时间的延长而增加,同时浆液流动阻力增大,因此,在同等注浆压力下,浆液运移速度有下降趋势;在注浆前25 s,HM、THM1、THM2工况渗流流速曲线基本重合,因为在注浆前期浆液温度属上升段且持续时间有限,因此,在注浆前期, 温度场的影响较小,此时温度场的影响可不予考虑;3种耦合工况与H工况渗流流速差别较大,在40 s时,H工况下的流速比耦合工况下的流速大约25%,说明注浆过程考虑浆液流动与多孔介质骨架相互作用非常有必要,其在注浆前期流固耦合效应占主导地位;在注浆持续200 s后, THM2工况浆液渗流流速骤降,因为THM2工况考虑了由于温度而引起的聚氨酯浆液粘度的变化,浆液发泡以后浆液粘度迅速增大,虽然浆液发泡膨胀产生二氧化碳气体,等同于增加了注浆压力,但浆液的粘度变化极为迅速,流动阻力迅速增大,导致浆液渗流流速迅速减小.综上,注浆过程前期流固耦合占主导地位,后期浆液温度达到一定值并持续一定时间引起聚氨酯浆液发泡膨胀,导致浆液粘度迅速改变,说明温度场对浆液的流动特性影响较大.
|
| 图 8 点流速变化图 Fig. 8 Point velocity variation |
与传统水泥基灌浆材料相比,高自生热材料的热流固耦合效应较为显著.以聚氨酯为分析对象,本文研究了其注浆过程的3场耦合效应影响.主要成果如下:
1) 在前人研究的基础上,利用渗流场、结构场、温度场3场控制方程及浆液密度、粘度、岩体孔隙率、渗透率、弹性模量等动态耦合变量,建立了注浆热流固3场全耦合数学模型,并应用该数学模型模拟注浆过程中热流固耦合效应.
2) 构建非均质孔隙及裂隙岩体介质模型,对注浆过程进行数值模拟得出:当裂隙开度大于孔隙介质等效微渗流通道宽度时,注浆压力扩散和温度热对流均优先在裂隙介质中传递,且裂隙开度越大,扩散效应越显著,通过参数化扫描裂隙开度大小并根据注浆压力云图扩散形态,可初步判断孔隙介质微渗流通道等效宽度的数量级,进而可对注浆对象细观及微观结构有一个初步认识.该结果对注浆前压水试验参数选取具有一定的指导作用,有利于进一步了解注浆对象的含水性和透水性能,可对注浆前水文地质调查数据作进一步完善和补充,本文算例采用的计算参数得出的孔隙介质渗流通道宽度的数量级为0.001 mm.
3) 数值计算发现,渗流场与结构场为强耦合关系,在注浆孔附近流固耦合效应随注浆时间增加而减弱;注浆过程聚氨酯浆液2次渗透前浆液自生热温度场对浆液渗流场及岩土体的热变形影响较为有限,为弱耦合关系,但聚氨酯浆液发泡膨胀产生二氧化碳,2次渗透后温度升高到一定值时,对浆液流动特性影响较大.温度在孔隙介质中的扩散范围虽然有限,但在裂隙介质中扩散较快致使裂隙介质中的温度较高,因此,高自生热浆材注浆在燃点温度较低的瓦斯抽采工程及节理裂隙较为发育的煤矿岩体中应用,应进行专门论证.
4) 注浆耦合工况和非耦合工况的数值分析表明,注浆方案设计中应使用注浆耦合动态参数代替传统注浆理论中的常数,如岩土体的渗透率、孔隙率、弹性模量以及浆液粘度和密度.
| [1] |
盛金昌, 廖秋林, 刘继山, 等. 基于FEMLAB的钻井过程中流固热耦合响应分析[J]. 工程力学, 2008, 25(2): 219-223. Sheng Jinchang, Liao Qiulin, Liu Jishan, et al. Analysis of coupled porothermoelastic response of a wellbore by using a FEMLAB-based simulator[J]. Engineering Mechanics, 2008, 25(2): 219-223. |
| [2] |
赵延林, 曹平, 赵阳升, 等. 双重介质温度场-渗流场-应力场耦合模型及三维数值研究[J]. 岩石力学与工程学报, 2007, 26(s2): 4024-4025. Zhao Yanlin, Cao Ping, Zhao Yangsheng, et al. Dual media model for thermo-hydro-mechanical coupling and 3d numerical simulation[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(s2): 4024-4025. |
| [3] |
Liu Quansheng, Zhang Chengyuan, Liu Xiaoyan. Numerical modelling and simulation of coupled THM processes in Task_D of DECOVALEX_IV[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(4): 709-720. |
| [4] |
张庆松, 张连震, 刘人太, 等. 基于"浆-土"界面应力耦合效应的劈裂注浆理论研究[J]. 岩土工程学报, 2016, 38(2): 323-330. Zhang Qingsong, Zhang Lianzhen, Liu Rentai, et al. Split grouting theory based on slurry-soil coupling effects[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(2): 323-330. |
| [5] |
郑卓, 李术才, 刘人太, 等. 裂隙岩体注浆中的浆液-岩体耦合效应分析[J]. 岩石力学与工程学报, 2015, 34(s2): 4054-4062. Zheng Zhuo, Li Shucai, Liu Rentai, et al. Analysis of coupling effect between grout and rock mass during jointed rock grouting[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(s2): 4054-4062. |
| [6] |
张龙云, 张强勇, 李术才, 等. 基于流固耦合的围岩后注浆对大型水封石油洞库水封性影响分析[J]. 岩土力学, 2014, 35(s2): 474-480. Zhang Longyun, Zhang Qiangyong, Li Shucai, et al. Analysis of impact of surrounding rock post-grouting for large oil cavern on its water seal ability based on fluid-solid coupling[J]. Rock and Soil Mechanics, 2014, 35(s2): 474-480. |
| [7] |
雷进生, 刘非, 王乾峰, 等. 非均质土层的注浆扩散特性与加固力学行为研究[J]. 岩土工程学报, 2015, 37(12): 2245-2253. Lei Jinsheng, Liu Fei, Wang Qianfeng, et al. Diffusion characteristics and reinforcement mechanics of grouting in non-homogeneous soil strata[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(12): 2245-2253. DOI:10.11779/CJGE201512014 |
| [8] |
石明生, 夏威夷. 聚氨酯高聚物注浆固化温度试验研究[J]. 化工新型材料, 2014, 42(7): 133-135. Shi Mingsheng, Xia Weiyi. Experimental research on curing temperature of polyurethane polymer[J]. New Chemical Materials, 2014, 42(7): 133-135. |
| [9] |
石明生, 王复明, 刘恒, 等. 堤坝高聚物定向劈裂注浆试验与有限元模拟[J]. 水利学报, 2016, 47(8): 1087-1092. Shi Mingsheng, Wang Fuming, Liu Heng, et al. Test and finite element simulation of directional splitting grouting of polymer in dam[J]. Journal of Hydraulic Engineering, 2016, 47(8): 1087-1092. |
| [10] |
孙培德, 杨东全, 陈奕柏. 多物理场耦合模型及数值模拟导论[M]. 北京: 中国科学技术出版社, 2007. Sun Peide, Yang Dongquan, Chen Yibai. Introduction to Coupling Models for Multiphysics and Numerical Simulations[M]. Beijing: Science and Technology of China Press, 2007. |
| [11] |
Cheng Pengda, Li Lu, Tang Ju, et al. Application of time-varying viscous grout in gravel-foundation anti-seepage treatment[J]. Journal of Hydrodynamics, 2011, 23(3): 391-397. DOI:10.1016/S1001-6058(10)60128-X |
| [12] |
陈鼎南, 陈童. 聚氨酯制品生产手册[M]. 北京: 化学工业出版社, 2014. Chen Dingnan, Chen Tong. Polyurethane Products Manual[M]. Beijing: Chemical Industry Press, 2014. |
| [13] |
李璐, 程鹏达, 钟宝昌, 等. 黏性浆液在小孔隙多孔介质中扩散的流固耦合分析[J]. 水动力学研究与进展, 2011, 26(2): 209-216. Li Lu, Cheng Pengda, Zhong Baochang, et al. Fluid-solid coupling analysis of grout in small porous medium[J]. Chinese Journal of Hydrodynamics, 2011, 26(2): 209-216. DOI:10.3969/j.issn.1000-4874.2011.02.010 |
| [14] |
Zhou Y, Rajapakse R K N D, Graham J. A coupled thermoporoelastic model with thermo-osmosis and thermal-filtration[J]. International Journal of Solids & Structures, 1998, 35(34): 4659-4683. |
| [15] |
李培超, 孔祥言, 卢德唐. 饱和多孔介质流固耦合渗流的数学模型[J]. 水动力学研究与进展, 2003, 18(4): 419-426. Li Peichao, Kong Xiangyan, Lu Detang. Mathematical modeling of flow in saturated porous media on account of fluid-structure coupling effect[J]. Chinese Journal of Hydrodynamics, 2003, 18(4): 419-426. DOI:10.3969/j.issn.1000-4874.2003.04.006 |
| [16] |
Bejan A. Convection in Porous Media[M]. Springer-Verlag New York, 2013.
|
| [17] |
Zhu Wancheng. Stress analysis of a borehole in saturated rocks under in situ mechanical, hydrological and thermal interactions[J]. Energy Sources, 2008, Part A(2): 157-169. |
| [18] |
冉启全, 李士伦. 流固耦合油藏数值模拟中物性参数动态模型研究[J]. 石油勘探与开发, 1997, 24(3): 61-65. Ran Qiquan, Li Shilun. Study on dynamic model of physical property parameters in fluid solid coupling reservoir numerical simulation[J]. Petroleum Exploration and Development, 1997, 24(3): 61-65. DOI:10.3321/j.issn:1000-0747.1997.03.015 |
| [19] |
雷进生.碎石土地基注浆加固力学行为研究[D].武汉: 中国地质大学, 2013. Lei Jinsheng. Research on mechanical behavior of grout in gravelly soil foundations[D].Wuhan: China University of Geosciences, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10491-1014150557.htm |
| [20] |
王伟力, 毕亚军, 钱七虎. 聚氨酯交联聚合反应体系粘度的变化[J]. 高分子材料科学与工程, 2001, 17(2): 72-75. Wang Weili, Bi Yajun, Qian Qihu. Viscosity changes of polyurethane reaction system during network polymerization[J]. Polymeric Materials Science and Engineering, 2001, 17(2): 72-75. DOI:10.3321/j.issn:1000-7555.2001.02.018 |
| [21] |
王永岩, 王艳春. 温度-应力-化学三场耦合作用下深部软岩巷道蠕变规律数值模拟[J]. 煤炭学报, 2012, 37(s2): 275-279. Wang Yongyan, Wang Yanchun. Numerical simulation of creep law in deep soft rock tunnel under thermal-mechanical-chemical coupling effect[J]. Journal of China Coal Society, 2012, 37(s2): 275-279. |
 2018, Vol. 51
2018, Vol. 51




