武汉大学学报(工学版)   2016, Vol. 49 Issue (2): 315-320

文章信息

张思建, 方彦军, 贺瑶, 肖勇
ZHANG Sijian, FANG Yanjun, HE Yao, XIAO Yong
基于模拟退火算法的AVS/RS多批货箱入库货位优化
Batches of container storage location assignment optimization in AVS/RS based on simulated annealing algorithm
武汉大学学报(工学版), 2016, 49(2): 315-320
Engineering Journal of Wuhan University, 2016, 49(2): 315-320
http://dx.doi.org/10.14188/j.1671-8844.2016-02-027

文章历史

收稿日期: 2015-06-23
 Abstract              PDF               Figures               Tables
引用本文 0
张思建, 方彦军, 贺瑶, 肖勇. 基于模拟退火算法的AVS/RS多批货箱入库货位优化[J]. 武汉大学学报(工学版), 2016, 49(2): 315-320.
ZHANG Sijian, FANG Yanjun, HE Yao, XIAO Yong. Batches of container storage location assignment optimization in AVS/RS based on simulated annealing algorithm[J]. Engineering Journal of Wuhan University, 2016, 49(2): 315-320.
基于模拟退火算法的AVS/RS多批货箱入库货位优化
张思建1, 方彦军2, 贺瑶2, 肖勇1     
1. 广东电网公司电力科学研究院，广东省智能电网新技术企业重点实验室，广东 广州 510080;
 2. 武汉大学动力与机械学院，湖北 武汉 430072
收稿日期: 2015-06-23
作者简介: 张思建(1983-)，男，博士，研究方向为电力测量先进技术，E-mail:zsjzju@foxmail.com.
摘要: 针对某计量检定中心对大量待检仪表的仓储需求，提出了基于模拟退火算法的自动小车存取系统(Autonomous Vehicle Storage and Retrieval Systems, AVS/RS)多批货箱入库货位优化分配方法.提出货位预分区策略，在提高货箱出入库节奏的同时使仓库整体货位安排也较为合理；根据货箱质量与周转率将货箱分类，分类数目与仓库货区分类数目相同，并采用模拟退火算法求解各类货箱与货区的对应关系；以出入库总能耗及存取效率为优化目标建立货位分配模型，采用模拟退火算法求解该模型得到最佳货位组合，并通过实例对比分析了采用不同方法对多批货箱入库能耗和效率的影响.
关键词： 自动化立体仓库     模拟退火算法     货位预分区     货位优化    
Batches of container storage location assignment optimization in AVS/RS based on simulated annealing algorithm
ZHANG Sijian1, FANG Yanjun2, HE Yao2, XIAO Yong1     
1. Guangdong Provincial Key Laboratory of Electric Power Research Institute of Smart Grid Technology, Guangdong Power Grid Corporation, Guangzhou 510080, China;
 2. School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China
Abstract: For the requirements of metrological center to store a large number of instruments which needed to be verified, a storage location assignment optimization method is proposed based on simulated annealing algorithm. Pre-partition strategy is proposed to improve the input-output efficiency and to make the overall arrangement in warehouse more reasonable. The containers are classified to several categories whose number is the same as the number of warehouse cargo area according to their weight and turnover, then solve the corresponding relationship between various types of container and cargo area with simulated annealing algorithm. The storage location assignment model is build by taking the total energy consumption and access efficiency as target; and then the model is solved with simulated annealing algorithm so as to get the optimal storage location. The method is compared with other methods through case study to analyze the impact of using different methods on total energy consumption and access efficiency.
Key words: AVS/RS     simulated annealing algorithm     storage pre-partition     storage location assignment optimization    

为保证电能计量资产管理的准确性并提高其检定效率，开展对电能计量资产仓储和配送的科学管理是十分必要的[1].鉴于电能计量器具的数量之大，表计变化状态之多，合理的仓储货位分配可有效提高表计存取效率，减少表计存取和拣选所需时间[2].

Roodbergen等[3]总结了过去30年自动化立体仓库的相关研究文献，指出常见的货位分配策略有以下5种：固定货位分配[4]、随机货位分配[5, 6]、离出库点最近货位分配、全周转货位分配[7-9]以及基于分类的货位分配[10].Hsiel S等[11]提出了一种面向BOM(Bill of Material)的分类货位分配方法，将货物分类存放至相应库区.Thonemann U W等[12]提出基于货物分类和应用周转率的方法解决随机环境中的货位分配问题.商允伟等[13]在研究货位分配问题时同时考虑货架稳定性和出入库操作的效率，采用改进的遗传算法解决这一多目标组合优化问题.银光球等[14]根据存取物资时能量消耗最小的原则，提出了货位优化数学模型，有效地解决现有存储模式存在的若干问题，降低仓库的运行成本.

上述文献研究大多建立在仓库初始状态为空的假定条件下，这显然不符合实际工程需求；即便是考虑仓库初始状态不为空的研究，也仅仅是进行了单批货物的入库仿真实验.而单批货物入库可选空货位范围较大，可以尽量选择最优的货位，这样很可能造成接下来几批货物入库时只能选择次优的货位而导致整体货位安排并不合理.算法方面，现有文献[13, 15, 16]大多采用遗传算法求解，该算法复杂且计算时间长，模拟退火算法相较遗传算法，极大地缩短了计算时间，更容易经过较少迭代次数得到最优解.

针对上述问题，本文针对非空AVS/RS进行多批货箱入库货位优化分配研究.采用货位预分区策略，对仓库货架进行整体分区，既减少了货位分配算法的计算时间，又使得仓库整体货物存放有一定的规程和条理.在对应货区进行货位分配时，同时考虑智能立库存取效率和存取能耗的货位分配控制策略，使之满足自动检定及配送的要求.

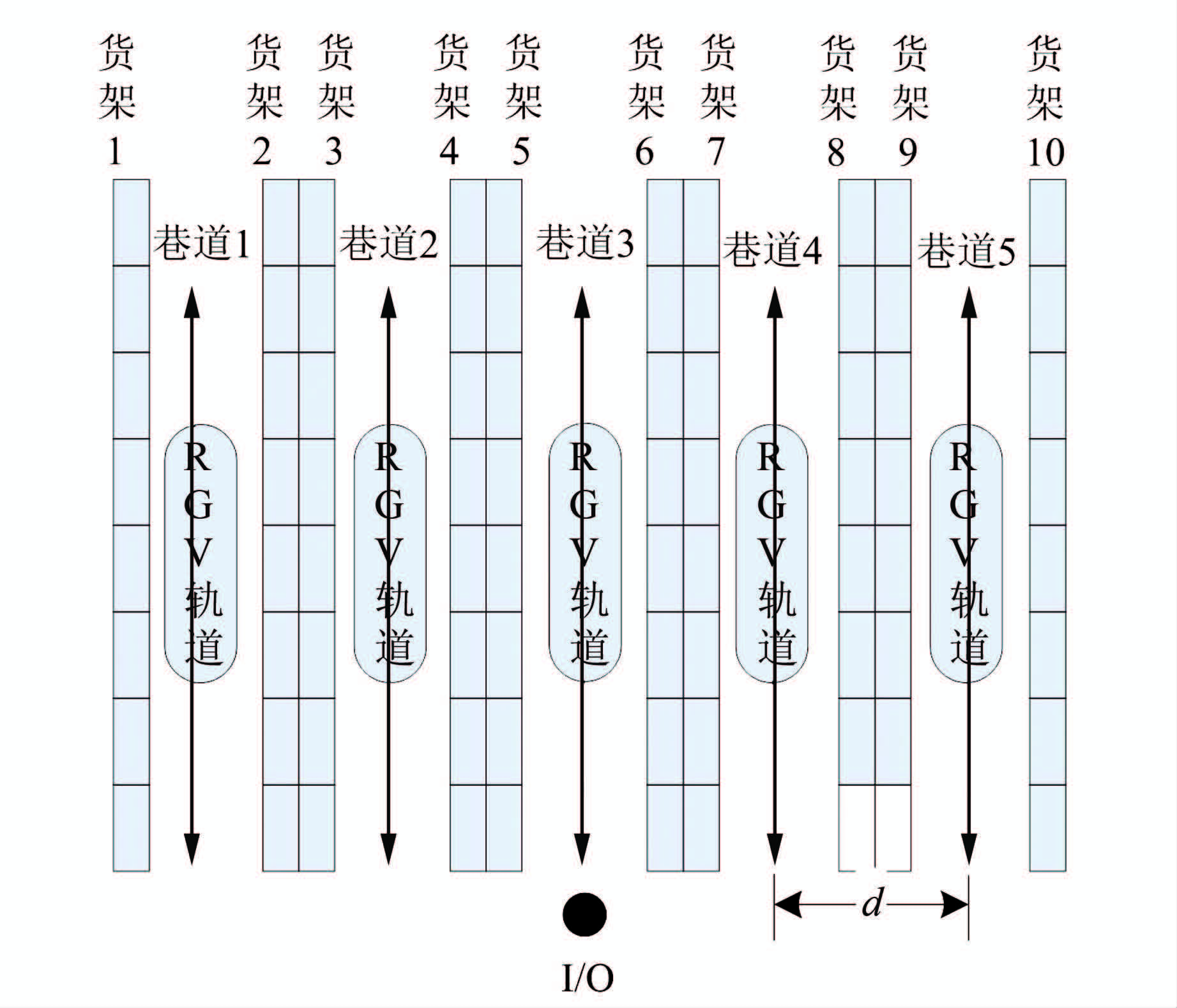
1 自动小车存取系统(AVS/RS)

与传统立体仓库采用堆垛机作业不同，自动小车存取系统利用轨道引导小车(Rail-guided Vehicles,RGV)在立体仓库货位间的轨道上运动实现货箱的出入库操作，其垂直运动依靠货架边缘的升降机实现.其示意图如图 1所示.

图 1 自动小车存取系统平面示意图 Figure 1 Sketch map of AVS/RS
图选项

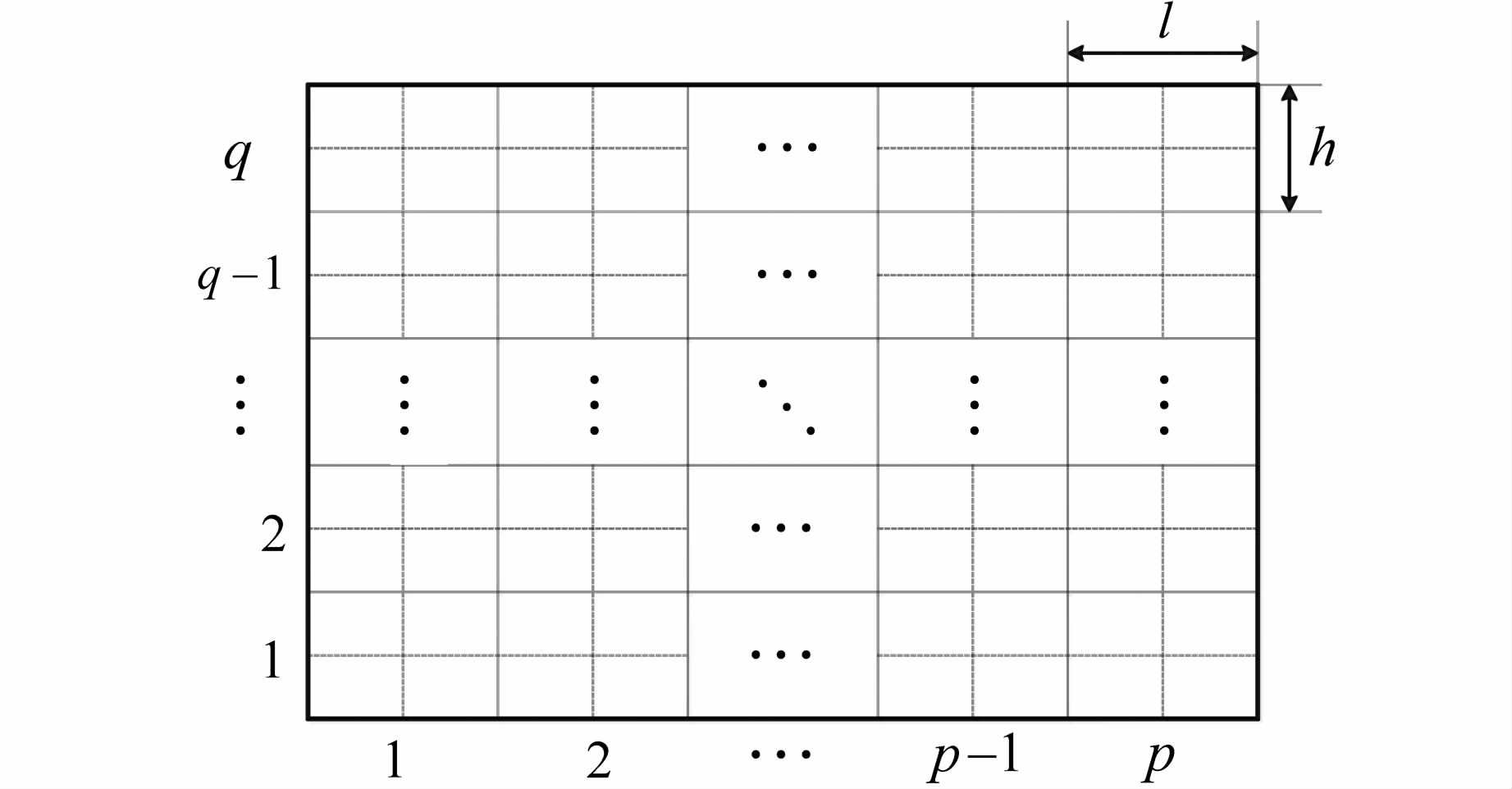
设仓库共有2r排货架，每排货架分为p列q层，小车入库点为I/O口，货架以I/O口与中间巷道形成的平面左右对称.将I/O口右侧货架定义为1~r排(离I/O口右侧最近的一排为1排)，将I/O口左侧货架定义为-r~-1排(离I/O口左侧最近的一排为-1排)；在每排货架中，将距离I/O最近的列记为第1列，最底层记为第1层.处于第k排第i列j层的货位记为(k,i,j)(k=-r,…,r;k≠0;i=1,2,…,p;j=1,2,…,q).在图 1中，货架4的第1列第5层即为(-2,1,5)，所有货位进行相应编码.设单个货位的高度为h，宽度为l.单排货架示意图如图 2所示.

图 2 单排货架示意图 Figure 2 Sketch map of single row shelf
图选项

在建立货位分配模型前，根据实际情况做出以下假定：

①忽略升降机所占空间；

②RGV进行出入库作业的起始位置在I/O口，RGV存取货箱时的作业位置在货位中心；

③运输货箱过程中RGV的启动和制动过程忽略不计，忽略RGV的存取时间，RGV运动过程中速度恒定；

④RGV一次只能存取一个货箱；

⑤仓库日常使用状态下货箱的存放种类、质量和周转率均已知；

⑥货架按最大承载能力设计，不考虑货架稳定性.

2 货架预分区

对于大型仓库来说，若无一定的存放规则，货箱的存储状况将显得杂乱无章，也不便于出库时的查找.若选择就近存放，后期入库的货箱将因被迫选择较远的货位而使整体能耗较高和耗费时间较长；若选择固定货位存放，在仓库设计阶段必须按照最大存货量设计，日常使用中将有大量的空货位处于闲置状态而使得资源浪费.因而对仓库中所有货位进行预分区，以提升仓库中各货位存放率，并使入库货箱得到有序存放.

对于某货位(k,i,j)，RGV从I/O口到该货位所需时间为

${{t}_{ijk}}=\frac{\left[ \left| \frac{k}{2} \right| \right]\cdot d}{{{v}_{x}}}+\frac{\left( i-\frac{1}{2} \right)\cdot l}{{{v}_{x}}}+\frac{\left( j-1 \right)\cdot h}{{{v}_{y}}}$    (1)

其中：k=-r,…,r;k≠0;i=1,2,…,p;j=1,2,…,q;|k|表示对货位的排号取绝对值，$\left[ \frac{\left| k \right|}{2} \right]$表示对$\frac{\left| k \right|}{2}$进行向下取整；d表示小车轨道在货架排之间的距离；l表示单个货位的长度；h表示单个货位的高度；vx、vy分别为小车在水平方向和垂直方向的运动速度.

RGV将单位质量货箱从I/O口运输至货位k,i,j消耗的能量为

$\begin{align} & {{e}_{ijk}}=\mu g\left( \left[ \left| \frac{k}{2} \right| \right]\cdot d \right)+\mu gl\cdot \left( i-\frac{1}{2} \right)+ \\ & g\left( j-1 \right)\cdot h \\ \end{align}$    (2)

其中：μ表示小车与轨道间的摩擦系数，g表示重力加速度.

从式(1)、(2)可以看出，RGV将单位质量货箱从I/O口运至货位(k,i,j)所需时间和能耗是一定的，与货箱本身无关，这两个值可以看作货位(k,i,j)的固有特性.将(1)、(2)两式相乘得到小车从I/O口到货位(k,i,j)的单位时间能耗函数：

$t{{e}_{ijk}}={{t}_{ijk}}\cdot {{e}_{ijk}}$    (3)

首先，根据货箱种类确定货架分区数.将仓库中日常作业的货箱分类，若货箱种类较少，则同种货箱归为一类；若货箱种类较多，则综合考虑货箱的质量和周转率，将货箱按质量与周转率之积从大到小分为n类.

其次，根据各货位的单位时间能耗函数值大小将货架划分为n个分区，每个单位时间能耗区间的货位属于同一个货区.设货位k,i,j对应的单位时间能耗积为teijk，根据实际情况设定某一阈值te，货位(k,i,j)所在分区由下式决定：

$\left( z-1 \right)\times te\le t{{e}_{ijk}}\le z\times te$    (4)

如果货位(k,i,j)满足该式，则说货位(k,i,j)属于z区z=1,2,…,n.无需强求所有货区内货位数相同，也可以各区设定不同阈值.

最后，采用模拟退火算法确定不同种类货箱与货区的对应关系.单位时间内RGV存取某种货箱的工作量与货箱本身的属性和货位属性均相关，将某种货箱的质量与周转率之积乘以某货区货位的单位时间能耗积作为衡量标准，建立如下数学模型：

$\min F=\sum\limits_{i=1}^{n}{\sum\limits_{\left( a,b,c \right)\in {{Z}_{{{S}_{i}}}}}{{{f}_{i}}\cdot {{m}_{i}}\cdot t{{e}_{abc}}}}$    (5)

其中：i表示第i类货箱；S表示1~n随机排列的一组数，Si表示这组数中第i个数；ZSi表示第Si个货区中的货位集合；(a,b,c)取遍ZSi中所有货位的坐标值；fi和mi分别表示第i类货箱的周转率加权平均和质量加权平均.

采用模拟退火算法求解式(5)得到解S，即货箱与货区的最佳对应关系.假设共有3类货箱，解S为2|3|1，则表示第1类货箱对应第2货区，第2类货箱对应第3货区，第3类货箱对应第1货区.

3 货位分配数学模型

根据货箱入库操作时间最短及总能耗最小原则，得到AVS/RS整体优化存储的数学模型为

$\left\{ \begin{matrix} \min \text{Time}=\sum\limits_{k=-r}^{r}{\sum\limits_{i=1}^{p}{\sum\limits_{j=1}^{q}{{{t}_{ijk}}{{x}_{ijk}}} }} \\ \begin{align} & \min \text{Energy}=\sum\limits_{k=-r}^{r}{\sum\limits_{i=1}^{p}{\sum\limits_{j=1}^{q}{{{e}_{ijk}}{{m}_{ijk}}{{x}_{ijk}}}}} \\ & \sum\limits_{k=-r}^{r}{\sum\limits_{i=1}^{p}{\sum\limits_{j=1}^{q}{{{x}_{ijk}}}}}=N \\ & {{x}_{kij}}=\left\{ \begin{matrix} 0 货位\left( k,i,j \right)为空 \\ 1货位\left( k,i,j \right)不为空 \\ \end{matrix} \right. \\ & k\ne 0 \\ \end{align} \\ \end{matrix} \right.$    (6)

其中：N是货箱的总数量，xkij用以表征货位状态.这里的货位优化问题是一多目标优化问题，采用加权法将多目标转化为单目标进行优化，优化公式为

$\left\{ \begin{matrix} \min \text{Obj}={{w}_{1}}\cdot \text{Time}+{{w}_{2}}\cdot \text{Energy} \\ {{w}_{1}}+{{w}_{2}}=1, 0＜{{w}_{1}}＜1 \\ \end{matrix} \right.$    (7)

其中：Obj为总目标值，w1为小车花费时间的权重，w2为小车消耗能量的权重.根据实际情况选择不同的权重组合.采用模拟退火算法求解该优化问题，先设定一组权重值，以某批待入库货箱中的x类货箱入库为例说明求解步骤，假设x类货箱对应第y货区.

Step1:编码.根据货位的特点，采用num×5(num是仓库中的总货位数)的矩阵Storage记录仓库中各货位状态，每一行表示一个货位，每行第1列表示货位的排号，第2列表示货位的列号，第3列表示货位的层号，第4列表示货位所属货区，第5列表示该货位的存储状态(0表示货位为空，1表示货位不为空).第4、5列用于待入库货箱在对应货区查找可分配空位.若某行为(-5,11,9,3,1)，则表示I/O口左边第5排第11列第9层的货位属于第3货区且该货位不为空.

Step2:找出y货区中的空货位记录于EmptyY，EmptyY比Storage多一列，用于记录EmptyY中的空货位在Storage中的行号，即索引值.

Step3:初始化.若待入库货箱中x类货箱有numx个，随机生成初始解S1，S1是从EmptyY的索引值中任选numx个随机排列组成1×numx的行向量.取初始温度T0足够大，令T=T0，确定每个T时的迭代次数，即Metropolis链长L.

Step4:对当前温度T和kL=1，2，…,L，重复步骤Step5~Step8.

Step5:随机产生一个新解S2，产生方法跟S1一样，判断S2与S1是否相同，若相同，重新产生新解S2，直到与S1不同为止.

Step6:计算S2的增量df=f(S2)-f(S1)，其中f(S1)为S1的代价函数.

Step7:若df＜0，则接受S2作为新的当前解，即S1=S2；否则计算S2的接受概率exp-df/T，即随机产生0,1区间上均匀分布的随机数rand，若exp-df/T＞rand，则接受S2作为新的当前解，S1=S2；否则保留S1.

Step8:判断是否满足终止条件，满足则输出当前解S1为最优解，结束程序.终止条件Stop通常为：在连续若干个Metropolis链中新解S2都没有被接受时终止算法，或是设定结束温度.否则按衰减函数衰减T后返回Step4.

Step9:将最优解S1根据索引值还原到Storage中对应的具体货位，并将相应货位的状态由0改为1.

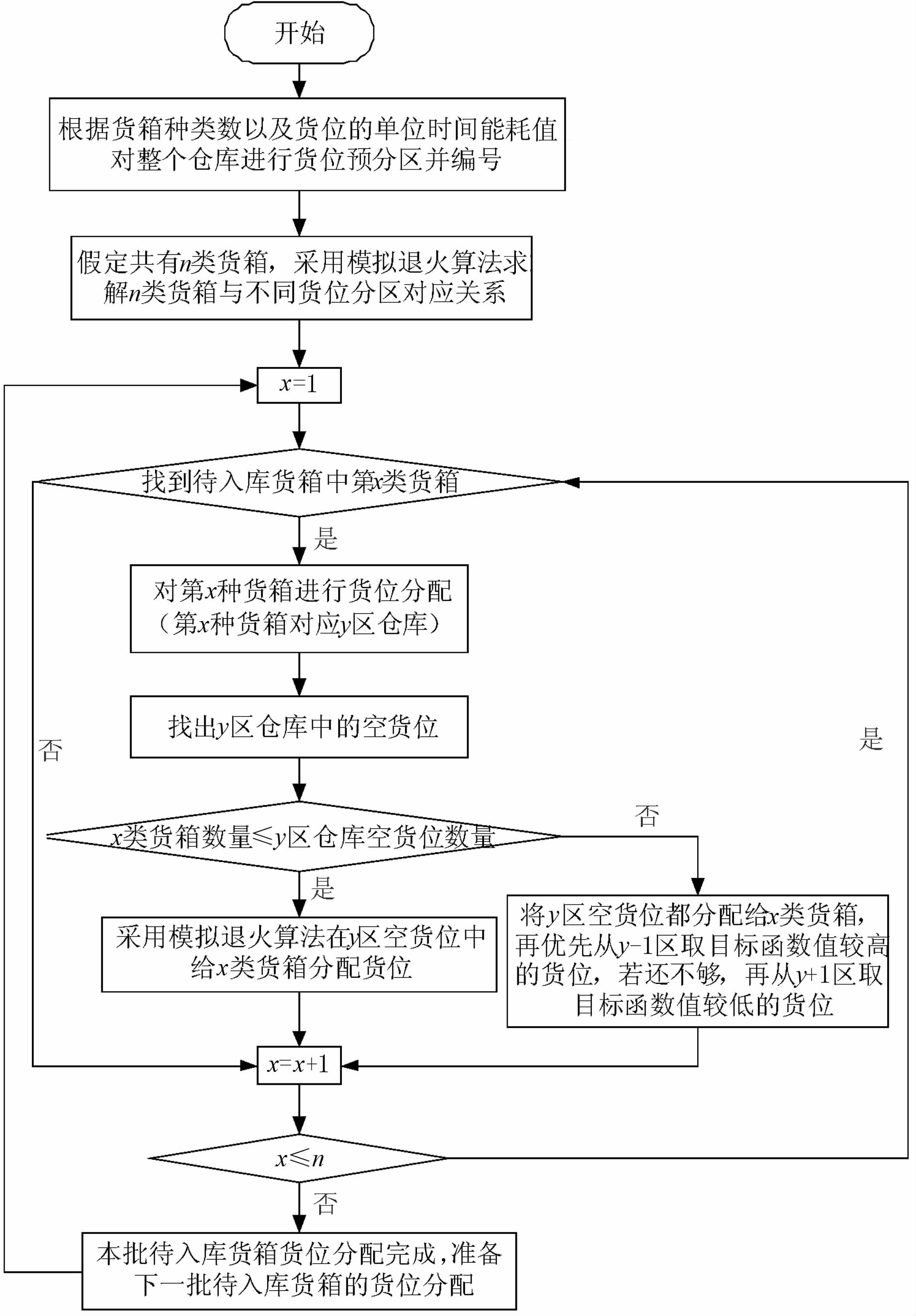
若待入库货箱对应分区空货位数不能满足实际要求，可就近向相邻货区索取货位.优先从低区选择目标值较高的货位，若仍不够，再从高区选择目标值较低的货位.多批货箱入库货位优化分配流程图如图 3所示.

图 3 多批货箱入库货位优化分配流程图 Figure 3 Flowchart of optimal allocation
图选项
4 货位优化分配实例

某计量检定中心仓库货架有10排13列23层，共2 990个货位，每个货位高1 m，宽2 m.小车轨道在货架排之间的距离为d=5 m，小车的水平速度和垂直速度分别为vx=3 m/s和vy=1 m/s.小车与轨道间的摩擦系数为0.1.

4.1 货位预分区仿真

日常存放货箱共有5类，其各自的周转率与质量如表 1所示.

表 1 货箱类别及其属性 Table 1 Categories and attributes of containers
货箱类别 周转率/% 质量/(kg/个)
1 3 150
2 4 200
3 5 230
4 10 240
5 16 100
表选项

根据第2节描述方法将仓库货架分为5个分区，分别标记为A~E区，其中A区货位单位时间能耗积最低，E区货位单位时间能耗积最高.采用模拟退火算法求解得到货箱与分区的对应关系.结果如表 2所示.

表 2 货箱类别与货架分区对应关系 Table 2 Congruent relationship of container attribute and shelf zone
货箱类别 1 2 3 4 5
对应分区 E D C B A
表选项
4.2 多批货箱入库货位优化仿真

在仿真试验中，模拟退火算法相关参数设定为：初始温度T0=1 000，终止温度Tend=10-3，各温度下的迭代次数(链长)L=200，降温速率q=0.9.由于仿真过程中发现Energy和Time的数值不在一个数量级上，因而引入 TE系数，如下式所示：

${{T}_{\text{E}}}=\frac{\sum\limits_{i=1}^{100}{\text{Energ}{{\text{y}}_{i}}}}{\sum\limits_{j=1}^{100}{\text{Tim}{{\text{e}}_{j}}}}$    (8)

其中：Energyi和Timej(i,j=1,2，…,100)分别为随机采样100个点对应的能量值和时间值.

改进后的优化公式为

$\left\{ \begin{matrix} \min \text{Obj}={{w}_{1}}\cdot \text{Time}\cdot {{T}_{E}}+{{w}_{2}}\cdot \text{Energy} \\ {{w}_{1}}+{{w}_{2}}=1, 0＜{{w}_{1}}＜1 \\ \end{matrix} \right.$    (9)

现有10批货箱等待入库，每批货箱各有50个.采用第3节描述方法对入库操作的货位进行优化分配.式(9)中w1分别取不同值对待入库货箱进行货位优化分配仿真，结果如表 3所示.

表 3 模拟退火算法多批货箱入库仿真结果(货位分区) Table 3 Simulation results of annealing algorithm
w1 w2 Time/s Energy/kJ Obj(×103) Runtime/s
0.1 0.9 7 159.7 9 770.5 9 509.4 80.21
0.2 0.8 7 121.3 9 792.9 9 258.6 78.68
0.3 0.7 7 097.7 9 802.7 8 991.2 88.38
0.4 0.6 7 049.0 9 809.6 8 705.4 78.43
0.5 0.5 7 021.0 9 838.5 8 429.8 78.46
0.6 0.4 6 995.3 9 872.0 8 146.0 81.87
0.7 0.3 6 965.3 9 908.4 7 848.2 84.93
0.8 0.2 6 925.3 10 055.7 7 551.4 83.60
0.9 0.1 6 919.3 10 106.5 7 238.0 84.16
表选项

若采用遗传算法对以上相同10批待入库货箱在整个仓库的空位进行货位分配，其结果如表 4所示.对比表 3和表 4可以看出，对于不同权重组合，模拟退火算法求得结果均优于遗传算法，且前者求解时间仅为后者的1/6左右，导致该结果的原因在于遗传算法易陷入局部最优，而模拟退火算法能够避免局部最优解.对于大规模仓库的在线货位分配模拟退火算法具有明显优势.

表 4 遗传算法多批货箱入库仿真结果(货位分区) Table 4 Simulation results of genetic algorithm
w1 w2 Time/s Energy/kJ Obj(×103) Runtime/s
0.1 0.9 7195 9834.5 9570.6 451.00
0.2 0.8 7168.0 9843.8 9308.7 474.14
0.3 0.7 7116.7 9862.2 9038.6 486.99
0.4 0.6 7140.3 9860.6 8772.5 531.64
0.5 0.5 7053.7 9898.5 8476.1 494.47
0.6 0.4 7023.0 9932.8 8186.9 530.98
0.7 0.3 6998.7 9993.4 7897.1 490.41
0.8 0.2 6988 10066.5 7599.3 502.33
0.9 0.1 6968 10128.6 7284.1 511.36
表选项

若不对仓库进行货位预分区处理，直接采用模拟退火算法对以上相同10批待入库货箱在整个仓库的空位进行货位分配，其结果如表 5所示.

表 5 模拟退火算法多批货箱入库仿真结果(未分区) Table 5 Simulation result of annealing algorithm without subregion
w1w2Time/sEnergy/kJ Obj/103
0.1 0.9 7 227.7 9 808.7 9 550.6
0.2 0.8 7 209.3 9 949.8 9 401.7
0.3 0.7 7 209.3 9 784.1 9 011.7
0.4 0.6 7 212.3 9 832.8 8 784.6
0.5 0.5 7 209.3 9 960.9 8 585.1
0.6 0.4 7 205.7 10 005.6 8 325.6
0.7 0.3 7 180.7 9 837.7 7 977.8
0.8 0.2 7 150.0 9 900.3 7 700.1
0.9 0.1 7 143.0 10 080.5 7 436.7
表选项

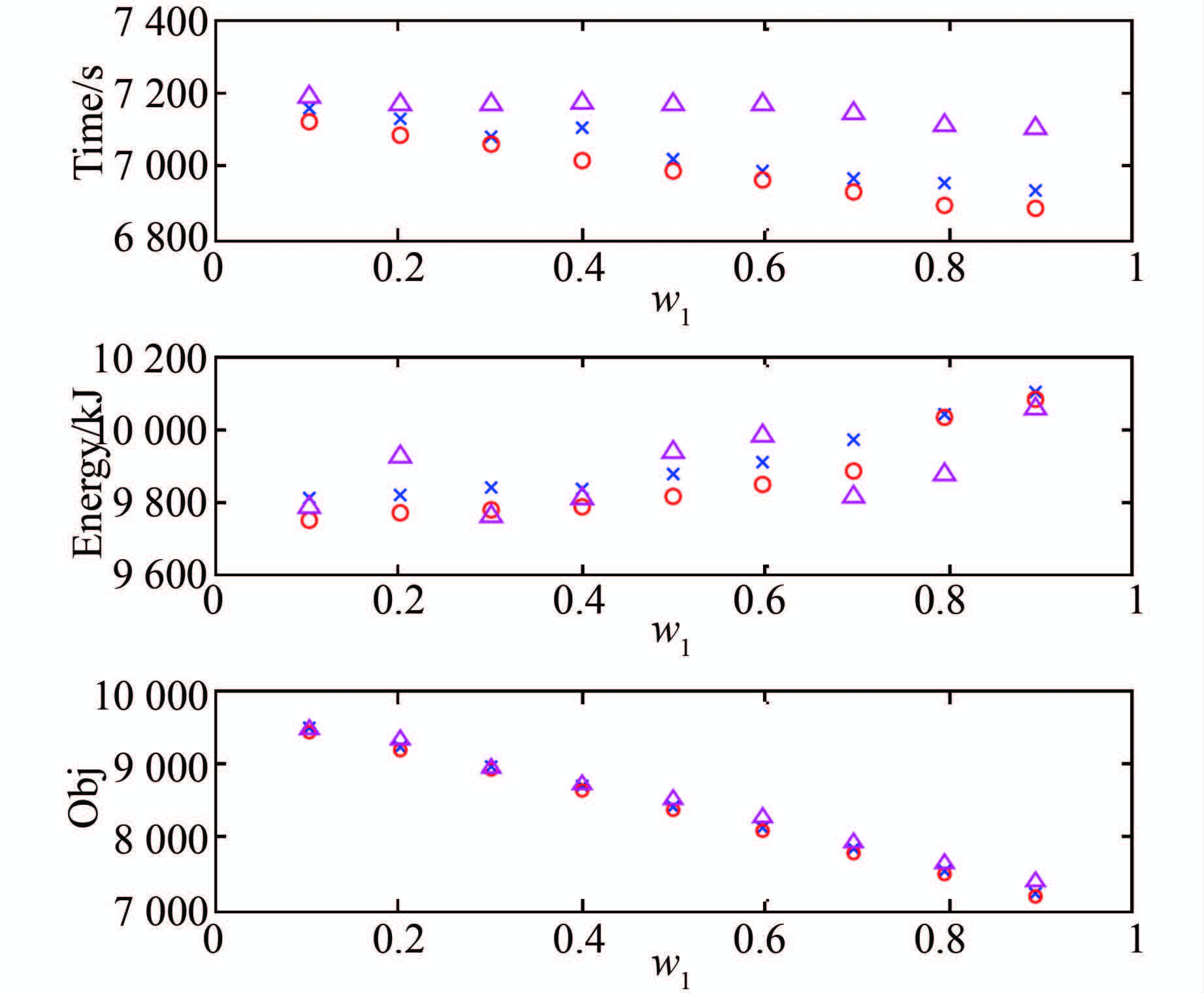
将表 3~5的数据在图 4中进行对比，“○”代表货位经过分区的仿真结果，“△”代表货位未经过分区的仿真结果.两者均采用模拟退火算法求解，区别仅在于是否进行货位预分区.“×”代表货位经过分区且采用遗传算法求解的结果.从图 4中可以看出：时间方面，经过货位预分区的货位分配结果明显优于未经过货位预分区的货位分配结果，模拟退火算法优于遗传算法；能耗方面，经过货位预分区的货位分配结果不具有明显优势，但其平均值相对较低，且在货位预分区情况下，模拟退火算法结果优于遗传算法；总目标值方面，经过货位预分区的仿真结果较优.

图 4 不同方法多批货箱入库货位优化目标值对比图 Figure 4 Comparison of different optimizing algorithms
图选项
5 结语

目前国内立体仓库货位分配的研究大多建立在空库基础上，即便是在仓库中有货的情况下为货物分配货位，也只进行了单批货物入库的仿真试验，结果无法证明该货位分配方法是否能在实际中使得整体目标最优.本文针对非空AVS/RS进行多批货箱入库货位优化分配研究.首先对仓库货架根据货位的单位时间能耗值进行整体分区，使相同货箱分巷道存放，减少小车在运输过程中发生碰撞；然后将日常存放于仓库的货箱根据质量与周转率进行分类，并找到各类货箱与货区的对应关系；最后采用模拟退火算法在对应货区对待入库货箱进行货位分配，提高其存取效率，降低存取能耗.采用不同方法进行实例仿真，基于模拟退火算法优化的货位分配方法明显优于随机货位分配方法，且经过货位预分区的方法优于未经过分区的方法.

参考文献
[1] 梁洪浩, 丁国茂. 面向未来电网的计量自动化系统存储技术研究[J]. 广东电力, 2012, 25(4): 22–26.
Liang Honghao, Ding Guomao. Research on storage technology of future grid oriented metering automation system[J]. Guangdong Electric Power, 2012, 25(4): 22–26.
[2] 林乃瑜, 林岳凌, 谭振豪. 电能表自动加封系统在计量检定流水线上的应用[J]. 广东电力, 2013, 26(11): 122–127.
Lin Naiyu, Lin Yueling, Tan Zhenhao. Application of electric energy meter automatic ensealing system in metrological verification pipeline[J]. Guangdong Electric Power, 2013, 26(11): 122–127.
[3] Roodbergen K J, Vis I F A. A survey of literature on automated storage and retrieval systems[J]. European Journal of Operational Research, 2009, 194(2): 343–362. DOI:10.1016/j.ejor.2008.01.038
[4] Atmaca E, Ozturk A. Defining order picking policy: A storage assignment model and a simulated annealing solution in AS/RS systems[J]. Applied Mathematical Modelling, 2013, 37(7): 5069–5079. DOI:10.1016/j.apm.2012.09.057
[5] Kuo P, Krishnamurthy A, Malmborg C J. Design models for unit load storage and retrieval systems using autonomous vehicle technology and resource conserving storage and dwell point policies[J]. Applied Mathematical Modelling, 2007, 31(10): 2332–2346. DOI:10.1016/j.apm.2006.09.011
[6] Hausman W H, Schwarz L B, Graves S C. Optimal storage assignment in automatic warehousing systems[J]. Management Science, 1976, 22(6): 629–638. DOI:10.1287/mnsc.22.6.629
[7] Lee M K. A storage assignment policy in a man-on-board automated storage/retrieval system[J]. The International Journal of Production Research, 1992, 30(10): 2281–2292. DOI:10.1080/00207549208948155
[8] Heskett J L. Cube-per-order index-a key to warehouse stock location[J]. Transportation and Distribution Management, 1963, 3(1): 27–31.
[9] Heskett J L. Putting the cube-per-order index to work in warehouse layout[J]. Transportation and Distribution Management, 1964, 4(8): 23–30.
[10] Chan F T S, Chan H K. Improving the productivity of order picking of a manual-pick and multi-level rack distribution warehouse through the implementation of class-based storage[J]. Expert Systems with Applications, 2011, 38(3): 2686–2700. DOI:10.1016/j.eswa.2010.08.058
[11] Hsieh S, Tsai K C. A BOM oriented class-based storage assignment in an automated storage/retrieval system[J]. International Journal of Advanced Manufacturing Technology, 2001, 17(9): 683–691. DOI:10.1007/s001700170134
[12] Thonemann U W, Brandeau M L. Optimal storage assignment policies for automated storage and retrieval systems with stochastic demands[J]. Management Science, 1998, 44(1): 142–148. DOI:10.1287/mnsc.44.1.142
[13] 商允伟, 裘聿皇, 刘长有. 自动化仓库货位分配优化问题研究[J]. 计算机工程与应用, 2004(26): 16–17.
Shang Yunwei, Qiu Yuhuang, Liu Changyou. Optimization of goods locations assignment of automated warehouse[J]. Computer Engineering and Applications, 2004(26): 16–17.
[14] 银光球, 何福英, 盛冬发. 自动化立体仓库中库位优化模型研究[J]. 福建工程学院学报, 2006, 4(3): 347–350.
Yin Guangqiu, He Fuying, Sheng Dongfa. Research on the storage alignment optimization model for automated stereoscopic warehouse[J]. Journal of Fujian University of Technology, 2006, 4(3): 347–350.
[15] 陈月婷, 何芳. 基于改进粒子群算法的立体仓库货位分配优化[J]. 计算机工程与应用, 2008, 44(11): 229–231.
Chen Yueting, He Fang. Location assignment optimization of AS/RS based on improved particle swarm optimization[J]. Computer Engineering and Applications, 2008, 44(11): 229–231.
[16] 马永杰, 蒋兆远, 杨志民. 基于遗传算法的自动化仓库的动态货位分配[J]. 西南交通大学学报, 2008, 43(3): 415–421.
Ma Yongjie, Jiang Zhaoyuan, Yang Zhiming. Dynamic location assignment of AS/RS based on genetic algorithm[J]. Journal of Southwest Jiaotong University, 2008, 43(3): 415–421.