文章信息
- 梁良, 李小勇, 刘俊, 巫世晶
- LIANG Liang, LI Xiaoyong, LIU Jun, WU Shijing
- 基于Mooney-Rivlin模型的车用橡胶衬套刚度计算及试验验证
- Stiffness calculation and experimental verification for automobile bushing based on Monney-Rivlin model
- 武汉大学学报(工学版), 2018, 51(1): 65-71
- Engineering Journal of Wuhan University, 2018, 51(1): 65-71
- http://dx.doi.org/10.14188/j.1671-8844.2018-01-010
-
文章历史
- 收稿日期: 2017-01-17
汽车底盘上安装有各式各样的悬置软垫,它们对减缓车辆的振动、提高行驶平顺性起着重要的作用.其主体是具有一定硬度的橡胶块,主要分布在发动机固定支架与车架之间、传动轴中间支撑以及前钢板弹簧盖板上等.动力总成悬置主要用于降低动力总成振动向车身传递、衰减由于路面激励引起的动力总成振动和控制动力总成位移和转角[1].如果这类软垫失效(硬化、破损或者脱落),则无法吸收车辆行驶中的颠簸,发动机运转时将发生振抖,且在汽车加速和制动时,发动机会前后窜动,导致飞轮壳等机件破裂,无法保证传动装置的平稳运转.
橡胶具有较高的内阻,又不会产生大的共振振幅,被广泛应用于减振设备中.Seibert从橡胶本构模型出发,分别研究了橡胶Arruda-Boyce模型、Van Der Waals模型、Yeoh模型之间的区别[2].Gracia研究了一种可以用于橡胶材料弹塑性分析的新模型[3].Hartmann通过试验验证了自己提出的一种获取橡胶本构模型材料参数的新方法[4].黄建龙利用Mooney-Rivlin模型和Yeoh模型对橡胶材料非线性特性进行了分析[5].
车用橡胶衬套一般由橡胶与金属层硫化而成,对于突然冲击和高频振动的吸收以及隔音具有良好的效果.同时橡胶衬套能够承受多向载荷共同作用,使系统机构简化,无需润滑,有利于维护与保养.Wang在考虑网格质量与单元特性的基础上,利用Mooney-Rivlin模型和Ogden模型对橡胶隔振器静态力-位移特性进行研究[6].D Sung利用参数识别的方法建立了悬架减振器橡胶衬套有限元模型[7].何小静利用测试得到的橡胶试片在不同状态下的应力-应变关系,拟合得到了不同橡胶本构模型的材料常数,研究橡胶隔振器静态力-位移的计算方法[8].王伟应用有限元软件计算减振器橡胶衬套径向、轴向、偏摆、扭转刚度和拉脱力[9].李季运用超弹性理论和有限元软件建立橡胶衬套有限元模型对其进行非线性特性分析[10].郭孔辉采用三向耦合的弹簧阻尼系统描述非对称式橡胶衬套的弹性耦合特性,并将其用于整车性能仿真中[11].方明霞利用试验和有限元相结合的方法,以最大应变能密度作为参数,预测汽车橡胶衬套疲劳寿命[12].上官文斌以橡胶悬置寿命预测为研究目标,以应变能密度、最大主Green-Lagrange应变和有效应力为损伤参量建立3种疲劳寿命预测模型,分析该3种建模方法优缺点[13].王文涛发现橡胶材料的拉伸疲劳寿命曲线与简单剪切疲劳寿命曲线的变化趋势一致、形状类似、拟合函数幂指数十分接近,并提出张量形式的疲劳寿命预测公式,有效地预测橡胶悬置疲劳寿命[14].
橡胶衬套的刚度设计对车辆传动装置的平稳运转起重要的作用,如果橡胶衬套刚度无法满足设计要求,车辆在运转过程中必然会发生摆振、噪音等现象.如何获取精确的橡胶衬套参数,不仅是橡胶衬套设计过程中的难点,同时也是整车动力学特性分析的重要环节.本文将从橡胶衬套本构关系出发,建立2参数Mooney-Rivlin超弹性材料模型,研究动力总成橡胶悬置的静刚度与动刚度特性,并将仿真结果与试验结果相比较,验证本文所提出模型的准确性.
1 橡胶衬套模型橡胶材料性能接近于高分子超弹性材料,对于超弹性材料,一般不用杨氏模量和泊松比表示应力-应变关系,而用应变能来表达应力-应变关系[15].橡胶超弹性力学模型是基于各向同性、等温性假说的,用一个统一的物理量来对橡胶进行表征,这个物理量就是应变能密度函数W,描述橡胶类材料具体应变能函数的种类很多.
利用有限元技术研究橡胶衬套非线性特性,首先要获取橡胶材料的力学性能数据,数据越全面表征的橡胶材料越真实,而据此设计的结构也越接近实际,橡胶材料力学性能数据包括单轴拉/压数据、双轴拉/压数据、平面剪切拉/压数据、体积拉/压数据.由于双轴、平面剪切、体积拉/压数据不容易测得,所以提供完整的材料力学性能数据比较困难[16].多数情况下则通过现有的橡胶材料本构模型进行橡胶衬套非线性特性分析,并结合试验数据进行验证.现有橡胶本构模型包括:Mooney-Rivlin,2阶多项式,1、2、3阶Ogden,Neo-Hookean,2阶缩减多项式和Yeoh模型以及基于热力学统计的Van der Waals模型.
研究表明:1阶Ogden模型曲线与2阶多项式模型在小应变情况下与试验数据吻合较好,而当应变大于0.5时,失真情况严重;Neo-Hookean模型在应变小于0.5时与试验情况吻合,当应变继续增大时与试验误差较大;2阶缩减多项式和Yeoh模型比Neo-Hookean模型情况要好,但当应变较大时也出现了与试验数据相差较大的情况,且其应变趋势与试验数据不符;Van der Waals模型比2阶缩减多项式和Yeoh模型稍好,但当应变较大时材料不稳定;2、3阶Ogden模型和Mooney-Rivlin模型在所有应变段都与试验数据吻合较好,即使应变较大时也未出现材料不稳定情况.
最初的橡胶衬套模型是一个简单黏弹型Kelvin-Voigt模型,其特性由同轴位移-力曲线来描述,这种模型建立在橡胶各个方向自由度是相互独立的基础上.Dzierek基于试验测试,将橡胶衬套模型简化为弹簧、黏性阻尼和摩擦阻尼组成[17].由于这种模型只有3个参数,在模型精度和参数的最小化之间达到了一个很好的平衡,被广泛应用.本文采用2参数Mooney-Rivlin超弹性材料模型方程(1)~(4)来模拟橡胶,利用ABAQUS/STANDAR来求解橡胶衬套刚度问题.
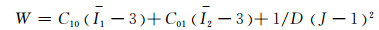 (1)
(1)
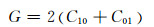 (2)
(2)
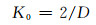 (3)
(3)
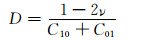 (4)
(4)
其中:C10、C01、D为材料参数;G、K0分别为初始剪切模量和初始体积模量;ν为泊松比.通过拟合获得橡胶衬套Mooney-Rivlin常数为:C10=0.494 7,C01=0.063 9,D=0.02.
2 有限元模型建立为获得理想的汽车平顺性性能,各生产厂商根据设计需要,设计了各方向具有不同力学性能的橡胶衬套.本文所研究的是一款车用发动机悬置衬套,它是一对称圆柱形橡胶衬套,如图 1所示.整个衬套由外钢圈、内钢圈以及中间橡胶层组成,其中橡胶通过硫化的方式与内外钢圈粘联,橡胶衬套则通过支架分别与车架和发动机联结.

|
| 图 1 发动机悬置橡胶衬套 Figure 1 Bushing for engine suspention |
在建立橡胶衬套有限元模型时,为了保证计算精度和计算效率,采用三维六面体单元C3D8RH和少量五面体单元C3D6H模拟橡胶结构.同时考虑橡胶衬套工艺需求,划分网格时尽可能保留橡胶衬套结构边缘处倒角,真实模拟橡胶衬套中存在的较复杂的发生于三维曲面上的内接触问题.最后结合橡胶衬套自身结构对称性特点,对橡胶衬套1/4模型进行网格划分,在划分完单元后,再对单元进行前后、左右镜像处理,以获得整个橡胶衬套有限元模型.这样做的目的是为了保证在计算过程中,不会因为对称面的单元形状不一致而导致计算结果发生畸变.图 2所示为橡胶衬套有限元模型,整个模型是由232 616个单元、243 350个节点组成.其中六面体单元213 694个,占单元总数的91.87%,满足计算精度要求.

|
| 图 2 发动机悬置橡胶衬套有限元模型 Figure 2 Finite element model of bushing |
由于钢的弹性模量几十甚至数百倍于橡胶,因此在分析橡胶衬套的静刚度时,将钢支架、钢轴以及硫化于橡胶内外表面的钢外圈视为刚体.参考试验工况对橡胶衬套进行边界条件加载,具体为:约束橡胶衬套外圈的所有自由度,载荷施加于与橡胶内圈固结的刚性轴上,刚性轴与橡胶之间采用多点约束来模拟硫化固结.本文采用中心节点位移作为输入条件,通过计算获取在对应的位移值下的橡胶衬套刚性轴作用反力.橡胶衬套静刚度具体加载量如表 1所示.
| 方向 | 位移/角度变化量 |
| X/mm | ±8 |
| Y/mm | -7~10 |
| Z/mm | ±7.5 |
| RX/(°) | ±20 |
| RY/(°) | ±8 |
| RZ/(°) | ±12 |
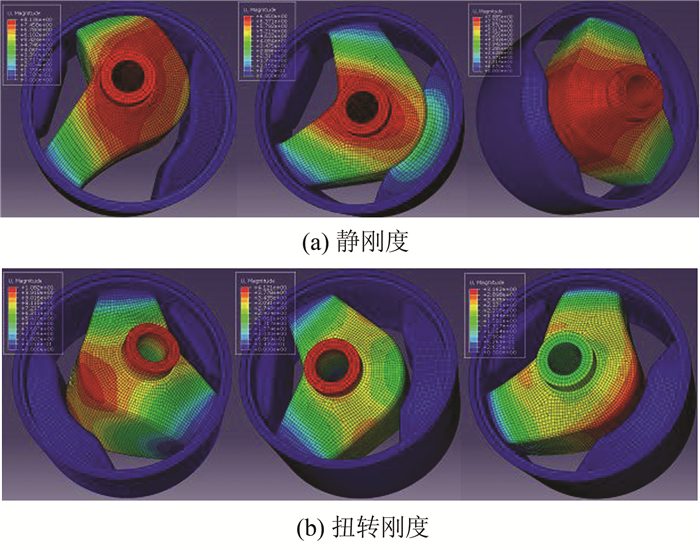
采用Mooney-Rivlin模型定义橡胶衬套有限元模型,求解计算该橡胶衬套在X、Y、Z三个方向静刚度,以及RX、RY、RZ三个方向扭转刚度,如图 3所示.计算时,将Abaqus求解器中的Nlgeom打开,载荷步增量设为0.01;记录中心轴的位移(旋转角)与作用反力(反力矩).
|
| 图 3 橡胶衬套X、Y、Z三个方向刚度 Figure 3 Stiffnesses of bushing in X, Y, Z directions |
发动机橡胶衬套在实际工作过程中始终处于受压状态,同时受到来自发动机工作振动以及路面不平度带来的随机振动等多种振动综合作用.因此,仅利用有限元模型研究橡胶衬套3个方向静态刚度以及扭转刚度无法完整地表达橡胶衬套工作时的非线性特性,必须利用该模型结合静刚度计算结果,研究橡胶衬套在一定预载条件下的动刚度特性.
假设橡胶衬套在预载F0作用下受外界激振,有
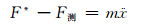 (5)
(5)
式中: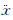
根据橡胶衬套动刚度定义可知:
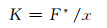 (6)
(6)
假定:x=x0sin(ω0t),同时假定橡胶材料相位角为φ0,那么橡胶衬套动刚度公式为
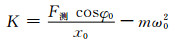 (7)
(7)
由式(7)可知,只要获得橡胶衬套激振力F测、相位角φ0、激振频率ω0、激振幅值x0、当量质量m,即可计算橡胶衬套在该预载条件下的动刚度.
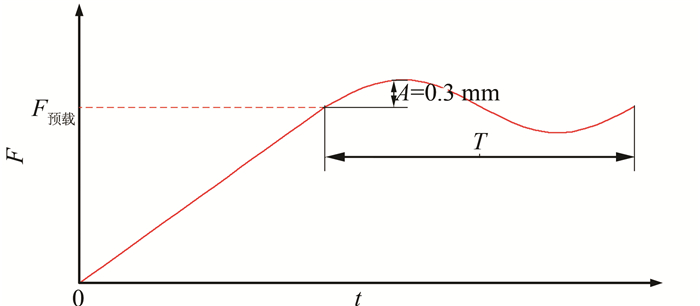
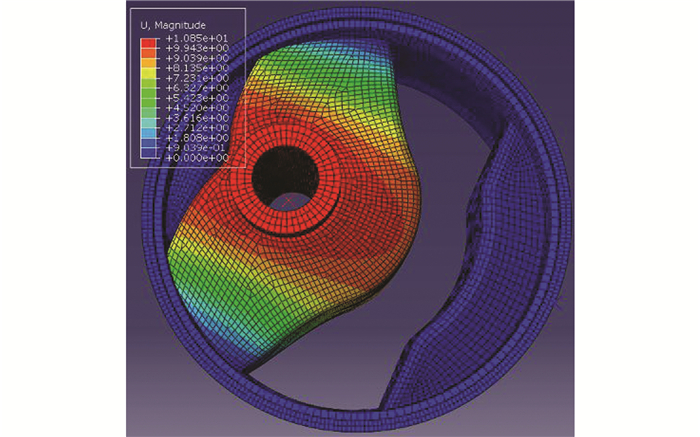
计算工况根据SAE行业标准,对本文橡胶衬套各方向施加300、1 000 N及F预载3种预加载荷,研究在该预加载荷作用下,橡胶衬套在振幅0.3 mm、激振频率由2 Hz变化到40 Hz时的动态特性,如图 4所示.具体动刚度施加曲线如图 5所示,其中F预载选取橡胶衬套线性区域最大刚度的60%作为预载力.图 5所示为预载650 N、激振频率为10 Hz时橡胶衬套的动刚度示意图.
|
| 图 4 动刚度边界条件加载示意图 Figure 4 Sketch of dynamic stiffness boundary loading |
|
| 图 5 预载650 N时橡胶衬套Y方向动刚度 Figure 5 Dynamic stiffness of bushing in Y-direction with 650 N |
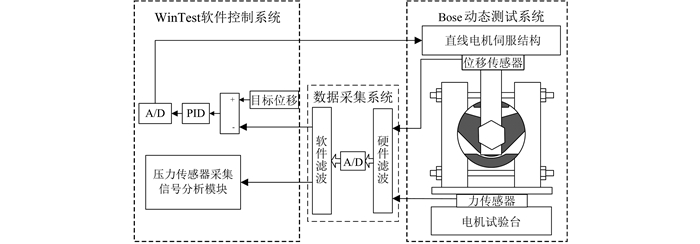
试验所使用的设备为美国Bose公司研发的ElectroForce动态测试试验平台.该试验平台由3个测试系统组成:WinTest软件控制系统、数据采集系统以及Bose动态测试系统.试验台顶部直线电机能够采用一定的频率进行加载,使橡胶衬套在某一特定位移范围内往复运动,同时测试系统的数据采集部分记录橡胶衬套力与位移(或速度)的关系.试验原理如图 6所示.
|
| 图 6 橡胶衬套刚度测试原理图 Figure 6 Principle diagram of stiffness test for bushing |
利用专用夹具将试验衬套固定在试验台上,装夹时采用自上而下安装,如图 7所示.这样保证橡胶衬套在安装过程中处于松弛状态,避免出现预紧力对试验结果的影响.

|
| 图 7 橡胶衬套刚度测试现场 Figure 7 Stiffness test site of bushing |
由于橡胶材料具有弹性迟滞现象,即在循环载荷作用下加载与卸载曲线不同,每次循环中加载与卸载所构成的环形面积表示在这次循环过程中所耗掉的能量,主要以热能的形式耗散.试验测试过程中,应尽可能避免橡胶弹性迟滞现象的发生.因此在试验测试过程中尽可能地采用相对较低的频率来驱动直线电机工作,最终保证橡胶衬套中心轴在相对较低的速度下运动.本文采用的测试频率为0.01 Hz.同时为避免加载过程中因载荷方向改变导致对测试结果的影响,测试时采用标准sin函数进行加载.结合橡胶衬套具体尺寸以及测试设备极限载荷,具体加载参数如表 2所示.
| 方向 | 测试幅值 |
| X/mm | ±7.5 |
| Y/mm | -6~12 |
| Z/mm | ±6 |
| RX/(°) | ±5 |
| RY/(°) | ±5 |
| RZ/(°) | ±5 |
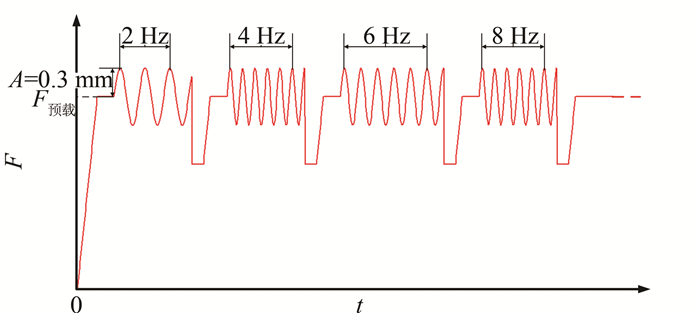
利用试验台对橡胶衬套进行动刚度试验测试时,WinTest软件控制系统直接提供了动刚度测试模块,只需要对橡胶衬套动刚度预加载荷、激振频率范围以及激振幅值进行定义.系统直接根据定义的数据进行某一预加载荷条件下扫频测试,记录相关试验数据,并通过后台程序直接进行橡胶衬套非线性特性分析.系统每次预加载荷扫频示意图如图 8所示.为了防止橡胶迟滞现象对测试结果的影响,系统在每次扫频结束、下一次扫频开始前,都要对橡胶衬套进行一次卸载,卸载后经过一定时间的稳定,重新加载至设定的预加载荷位置,再进行扫频测试.
|
| 图 8 橡胶衬套动刚度试验扫频示意图 Figure 8 Sketch of frequency sweep for dynamic stiffness test |
从仿真曲线与试验曲线对比图可以看出,不管是静刚度曲线还是扭转刚度曲线,橡胶衬套的仿真曲线与试验曲线吻合较好,说明本文所建立的2参数Mooney-Rivlin橡胶衬套模型具有一定精度.从表 3橡胶衬套仿真值与试验值对比可以看出,除Y负方向以及X轴扭转外,其余几个方向的刚度值误差均在10%以内,部分误差甚至控制在5%以内,进一步说明本文所采用的建模方法有一定正确性.
| 类型 | 方向 | 仿真值 | 试验值 | 误差/% |
| 静 刚 度 |
X/(N·mm-1) | 240.42 | 253.80 | 5.3 |
| Y正方向/(N·mm-1) | 107.55 | 101.10 | 6.4 | |
| Y负方向/(N·mm-1) | 208.10 | 251.65 | 17.3 | |
| Z/(N·mm-1) | 65.10 | 61.43 | 6.0 | |
| 扭转 刚度 |
RX/(Nm·(°)-1) | 0.344 | 0.475 | 27.6 |
| RY/(Nm·(°)-1) | 0.975 | 0.947 | 3.0 | |
| RZ/(Nm·(°)-1) | 0.700 | 0.640 | 9.4 |
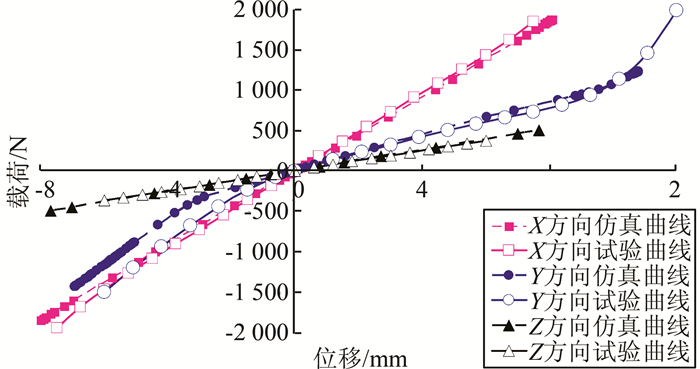
Y轴负方向刚度误差值达到了17.3%,且试验测试刚度大于仿真值,这是由于所建立的橡胶衬套有限元模型与试验测试用的橡胶衬套不一致导致的,在实验测试过程中,橡胶衬套轴心橡胶较早地与底部橡胶发生接触而改变了橡胶刚度,而在有限元模型中衬套轴心要经过一定的位移才能与底部橡胶发生接触.从图 9可以看出,两条Y负方向的刚度曲线在橡胶衬套接触后半段的斜率基本一致(该位置处仿真值刚度为268.4 N/mm,试验值刚度为276.8 N/mm),只是发生了2 mm左右的位移,这一位移量恰好是仿真模型需要经过2 mm才与衬套底部橡胶发生接触,而试验测试时橡胶衬套在开始时刻直接与衬套底部橡胶发生接触.从实际图片与橡胶衬套三维模型(图 1所示)也可以发现这一问题,试验测试用的橡胶衬套在该位置处几乎没有间隙,而三维模型中该位置有一定的间隙量.
|
| 图 9 橡胶衬套X、Y、Z方向静刚度对比 Figure 9 Static stiffness in X, Y, Z directions |
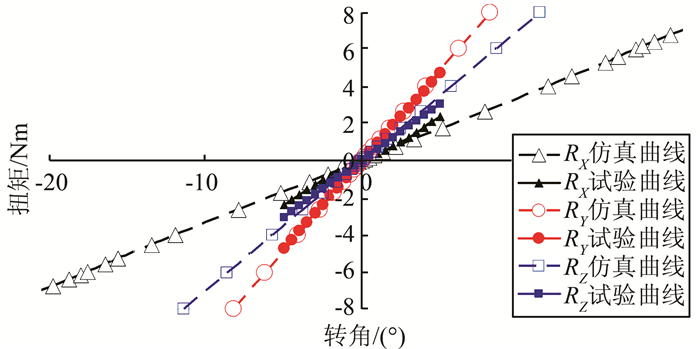
而对于X方向的扭转刚度来说,试验测试值要大于仿真值,如图 10所示.这是由于前面所提到的2 mm间隙量导致的,由于在测试X方向扭转时,试验用的橡胶衬套过早地与底端的橡胶发生接触而导致刚度增大,而仿真模型则需要经过一定的角度变化才能与底部橡胶发生接触.而这一间隙量的存在不影响其他两个方向的扭转与静刚度测试与仿真,足以说明本文所建立的橡胶衬套刚度计算模型具有一定的精度.
|
| 图 10 橡胶衬套X、Y、Z扭转刚度对比 Figure 10 Torsional stiffness in X, Y, Z directions |
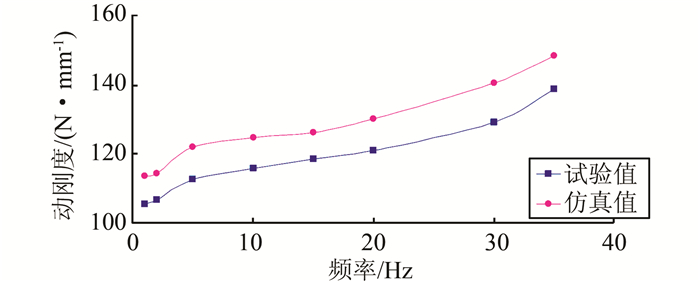
图 11所示为橡胶衬套在650 N预载作用下,Y轴正方向动刚度仿真值与试验值对比,从图中可知仿真值与试验值的趋势基本一致,仿真值较试验值偏大,这与该橡胶衬套在Y方向的静刚度的仿真值大于试验值结论一致.表 4列出了典型频率下橡胶衬套动刚度仿真值与试验值,从表中可以看出仿真值与试验值误差控制在10%以内,进一步说明本文所建立的模型具有一定的精度.
|
| 图 11 橡胶衬套动刚度曲线 Figure 11 Dynamic stiffness curves of bushing |
| 频率/Hz | 动刚度/(N·mm-1) | 误差/% | |
| 仿真值 | 试验值 | ||
| 2 | 106.5 | 114.1 | 6.6 |
| 10 | 115.7 | 124.5 | 7.1 |
| 20 | 120.8 | 130.0 | 7.1 |
| 30 | 128.9 | 140.3 | 8.1 |
发动机橡胶衬套可以减小发动机振动向车身传递、控制发动机位移和转角、衰减路面激励引起的发动机振动、提高汽车行驶平顺性.以发动机橡胶悬置为研究对象,利用2参数Mooney-Rivlin橡胶衬套模型和有限元分析软件ABAQUS建立橡胶衬套仿真模型;通过仿真计算获得橡胶衬套X、Y、Z三个方向静刚度及扭转刚度,揭示橡胶衬套动刚度特性;并结合试验分析误差产生原因,验证所建立模型的准确性.该建模方法不仅可以用来研究橡胶衬套非线性特性,降低橡胶衬套研发成本,缩短研发时间,还有助于整车动力学特性研究.
| [1] | Suangguan Wenbin. Engine mounts and powertrain mounting systems:A review[J]. International Journal of Vehicle Design, 2009, 49(4): 237–258. DOI:10.1504/IJVD.2009.024956 |
| [2] | Seibert D J, Schoche N. Direct comparison of some recent rubber elasticity model[J]. Rubber Chemistry and Technology, 2000, 73(2): 366–384. DOI:10.5254/1.3547597 |
| [3] | Gracia L A, Liarte E, Pelegay J L, et al. Finite element simulation of the hysteretic behavior of an industrial rubber[J]. Finite Elements in Analysis and Design, 2010, 46(4): 357–368. DOI:10.1016/j.finel.2009.12.002 |
| [4] | Hartmann S, Tschope T, Schreiber L, et al. Finite deformations of a carbon black-filled rubber: Exeriment optical measurement and material parameter identification using finite elements[J]. European Journal of Mechanics, 2003, 22(3): 309–324. DOI:10.1016/S0997-7538(03)00045-7 |
| [5] |
黄建龙, 解广娟, 刘正伟. 基于Mooney-Rivlin模型和Ogden模型的超弹性橡胶材料有限元分析[J].
橡塑技术与装备, 2008, 55(8): 467–471.
Huang Jianlong, Xie Guangjuan, Liu Zhengwei. Finite element analysis of super-elastic rubber materials based on the Mooney-Rivlin and Yeoh model[J]. Rubber/Plastics Technology and Equipment, 2008, 55(8): 467–471. |
| [6] | Wang L R, Lu Z H. Modeling methods of constitutive law of rubber hyperelasticity based on finite element simulations[J]. Rubber Chemistry and Technology, 2003, 76(1): 271–285. DOI:10.5254/1.3547739 |
| [7] | Sung D, Jeong G, Joo S. An integrated approach to the development of suspension rubber bushing[Z]. SAE 2006-01-1623, 2006. |
| [8] |
何小静, 上官文斌. 橡胶隔振器静态力-位移关系计算方法的研究[J].
振动与冲击, 2012, 31(11): 91–97.
He Xiaojing, Shangguan Wenbin. Calculating methods for force versus displacement relation of a rubber isolator[J]. Journal of Vibration and Shock, 2012, 31(11): 91–97. |
| [9] |
王伟, 上官文斌. 悬架筒式减震器橡胶衬套刚度和拉脱力试验与计算分析[J].
橡胶工业, 2013, 60(3): 169–172.
Wang Wei, Shangguan Wenbin. Experiment and calculation analysis on stiffness and pull-out force of rubber bushing for suspension telescopic shock absorber[J]. China Rubber Industry, 2013, 60(3): 169–172. |
| [10] |
李季, 李秋实. 橡胶悬架弹簧建模与非线性特性分析[J].
农业装备与车辆工程, 2013, 51(5): 36–39.
Li Ji, Li Qiushi. Modeling and nonlinear characteristics analysis of rubber suspension spring[J]. Agricultural Equipment & Vehicle Engineering, 2013, 51(5): 36–39. |
| [11] |
郭孔辉, 王爽, 丁海涛, 等. 后悬架非对称式橡胶衬套弹性耦合特性[J].
吉林大学学报(工学版), 2007, 37(6): 1225–1228.
Guo Konghui, Wang Shuang, Ding Haitao, et al. Elastic coupling characteristic of unsymmetrical rubber bushings of rear suspension[J]. Journal of Jilin University(Engineering and Technology Edition), 2007, 37(6): 1225–1228. |
| [12] |
方明霞, 谈军, 许光. 汽车橡胶衬套随机疲劳分析[J].
汽车工程, 2013, 35(10): 949–954.
Fang Mingxia, Tan Jun, Xu Guang. Random fatigue analysis of vehicle rubber bushings[J]. Automotive Engineering, 2013, 35(10): 949–954. DOI:10.3969/j.issn.1000-680X.2013.10.018 |
| [13] |
上官文斌, 刘泰凯, 王小莉, 等. 汽车动力总成橡胶悬置的疲劳寿命实测与预测方法[J].
机械工程学报, 2014, 50(12): 126–132.
Shangguan Wenbin, Liu Taikai, Wang Xiaoli, et al. Methods for measuring and predicting fatigue life of rubber mounts of vehicle powertra[J]. Journal of Mechanical Engineering, 2014, 50(12): 126–132. |
| [14] |
王文涛, 上官文斌, 段小成, 等. 基于线性疲劳累计损伤橡胶悬置疲劳寿命预测研究[J].
机械工程学报, 2012, 48(10): 56–65.
Wang Wentao, Shangguan Wenbin, Duan Xiaocheng, et al. Study on prediction of fatigue life of rubber mount based on linear cumulative fatigue damage theory[J]. Journal of Mechanical Engineering, 2012, 48(10): 56–65. |
| [15] |
陈志勇, 史文库, 王清国. 基于材料试验的发动机橡胶悬置有限元分析[J].
汽车技术, 2010(7): 28–31.
Chen Zhiyong, Shi Wenku, Wang Qingguo, et al. Finite element analysis of engine rubber mount based on material test[J]. Automobile Technology, 2010(7): 28–31. |
| [16] |
康一坡, 霍福祥, 魏德勇, 等. 有限元技术在橡胶悬置正向开发中的应用[J].
汽车技术, 2014(6): 6–11.
Kang Yipo, Huo Fuxiang, Wei Deyong, et al. Application of FEM on the forward engineering design of rubber mounting[J]. Automobile Technology, 2014(6): 6–11. |
| [17] | Dzierzek S. Experiment-based modeling of cylindrical rubber bushings for the simulation of wheel suspension dynamic behavior[Z]. SAE 2000-01-0095, 2000. |
 2018, Vol. 51
2018, Vol. 51




