武汉大学学报(工学版)   2017, Vol. 50 Issue (4): 571-575

文章信息

郑亮, 尤阳, 李文政, 尹帅, 董彦莉
ZHENG Liang, YOU Yang, LI Wenzheng, YIN Shuai, DONG Yanli
联方网壳及其弦支结构的冲击性能
Performance of single-layer reticulated dome and suspendome under impact loading
武汉大学学报(工学版), 2017, 50(4): 571-575
Engineering Journal of Wuhan University, 2017, 50(4): 571-575
http://dx.doi.org/10.14188/j.1671-8844.2017-04-015

文章历史

收稿日期: 2016-01-28
 Abstract              PDF               Figures               Tables
引用本文 0
郑亮, 尤阳, 李文政, 尹帅, 董彦莉. 联方网壳及其弦支结构的冲击性能[J]. 武汉大学学报(工学版), 2017, 50(4): 571-575.
ZHENG Liang, YOU Yang, LI Wenzheng, YIN Shuai, DONG Yanli. Performance of single-layer reticulated dome and suspendome under impact loading[J]. Engineering Journal of Wuhan University, 2017, 50(4): 571-575.
联方网壳及其弦支结构的冲击性能
郑亮, 尤阳, 李文政, 尹帅, 董彦莉     
中北大学土木工程学科管理部，山西 太原 030051
收稿日期：2016-01-28
作者简介：郑亮(1977-)，男，博士，讲师，主要从事钢结构与组合结构研究，E-mail:zl_5403@126.com.
基金项目：国家自然科学基金青年基金项目(编号：51208473).
摘要：应用有限元软件ANSYS/LS-DYNA建立50 m跨度的单层联方球面网壳及其相应的弦支网壳的有限元模型并进行数值模拟分析，得到联方单层球面网壳及其相应弦支网壳的冲击力、位移及杆件应力随着冲击速度和冲击体重量变化的时程曲线变化规律.通过分析表明联方网壳及其弦支结构的冲击过程相类似，可以分为冲击阶段、稳定相持阶段和衰减阶段3个阶段；网壳杆件突然断裂会导致冲击力发生突然的变化；弦支结构相对于联方单层网壳而言，在相同的冲击速度和冲击重量的作用下，弦支结构可显著减小网壳的最大位移，增加网壳的抗冲击能力；弦支结构索力的增加可适当减小冲击产生的位移，但减小效果有限；径向杆件和环向杆件的冲击应力距离冲击点越远，冲击应力峰值及残余应力也越小.
关键词：网壳    冲击    动力响应    弦支网壳    
Performance of single-layer reticulated dome and suspendome under impact loading
ZHENG Liang, YOU Yang, LI Wenzheng, YIN Shuai, DONG Yanli     
School of Civil Engineering, North University of China, Taiyuan 030051, China
Abstract: Finite element model of a lamella single-layer reticulated dome and the suspendome with a span of 50 m are developed and analyzed by ANSYS/LS-DYNA. The time history curve of the impact force, displacement and rod stress are obtained by the finite element analysis software under the different impact velocities and the different weights. The analysis results show that impact process of a single-layer reticulated dome and the suspendome can divided into shock stage, stable stalemated stage and decay stage. Sudden fracture of the lattice shell may cause the sudden change of the impact force. The suspendome obviously reduce the peak value of displacement compared to a single-layer reticulated dome under the conditions of same velocity and weight. Increase of the cable force may be appropriate to reduce the impact displacement. The peak value of the impact stress and the residual stress of the radial and ring member are more and more small from the point of impact.
Key words: reticulated dome     impact     dynamic response     suspendome    

弦支结构体系由上部单层网壳、下部的竖向撑杆、径向拉杆和环向拉索组成，其中各环撑杆的上端与单层网壳对应的各环节点铰接，撑杆下端由径向拉索与单层网壳的下一环节点连接，同一环的撑杆下端由环向拉索连接在一起，使整个结构形成一个完整的体系.单层网壳及弦支结构广泛应用于大跨度空间结构中，而大跨度空间结构中人员较为密集[1]，如这些结构受到冲击荷载作用，将产生严重的后果.冲击荷载是一种偶然发生的荷载，这种荷载作用于结构的时间短、强度大、无法有效预测，同时结构也不可能完全具备抵抗这种荷载的能力.可以对这种荷载作用于结构的时间历程及其和结构单元体系交互作用的形态加以控制，最大程度降低破坏的过程和强度.目前对这种冲击方面的研究较少，文献[2-14]分别对冲击荷载下钢框架结构及网壳结构的性能进行了研究，但现阶段对弦支结构的研究还没有.本文研究单层网壳和弦支结构在冲击荷载作用下的力学性能和破坏形态，建立这种结构在冲击作用下的防御机制.利用有限元程序ANSYS/LS-DYNA对联方网壳及弦支结构在冲击荷载作用下的动态响应进行研究，以获得联方网壳及弦支在冲击荷载作用下的性能.

1 计算模型及其参数

网壳的数值模型由3部分组成：网壳、冲击体和节点集中质量.网壳单元采用3节点梁单元Beam161，屋面荷载通过等效采用质量单元Mass166施加，冲击体采用8节点6面体实体单元Solid164.拉杆和撑杆采用LINK10，该单元为三维桁架单元，只能承受轴向拉力和压力.索采用CABLE单元，该单元只能受拉，不能受压，而且也可直接施加预应力.

冲击块的材料模型采用刚性体模型Rigid Body，该模型在冲击过程中并不发生变形，可以大量节省计算时间，不影响计算结果.网壳与冲击体接触类型采用自动点面接触(nodes to surface).冲击体位于网壳模型上方1 m处，通过改变冲击体的初速度和质量，来模拟不同速度和重量对网壳结构的冲击.

钢材采用PLASTIC_ KINEMATIC材料模型模拟, 该材料模型可以模拟高速加载下钢构件的应力和应变.与静力加载相比, 在冲击荷载作用下, 材料的应变率非常高, 钢材的屈服强度有明显的提高.在高应变率下, 钢材抗拉强度可增大50%以上.国外已有的相关领域研究成果显示，应变率对结构承受动力冲击荷载的能力有重要影响[8-10], 因而要想得到比较可靠的模拟效果, 钢材的应变率效应不可忽略.其本构关系为

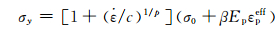    (1)

式中：σ0为初始屈服应力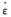；为应变率；εpeff为有效塑性应变；Ep为塑性硬化模量; 参数β取1(即等向强化)，c取40，p取5.

钢材屈服强度取为315 N/mm2, 弹性模量E为2.06 GPa, 泊松比υ为0.3，钢材的密度取为7 850 kg/m3.对于钢材的应变率效应, 通过设置式(1)中的参数c、p来考虑.索单元材料采用CABLE-BEAM(MAT_72), 该材料模型只能受拉而不能受压.

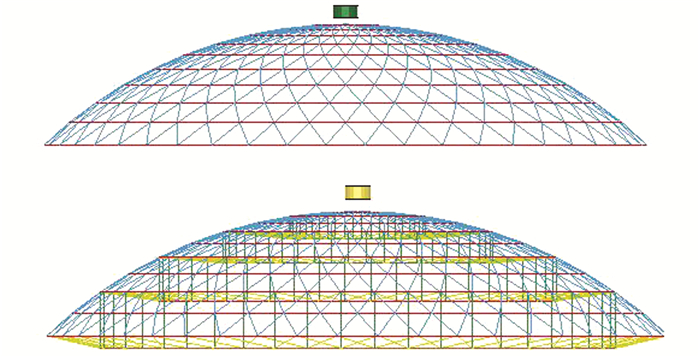
联方弦支网壳支座采用释放径向位移的约束铰支座.联方单层网壳采用3向铰支座，弦支采用间隔布置，如图 1所示.

图 1 联方网壳及弦支网壳初始状态 Figure 1 Initial states of single-layer reticulated dome and suspendome
图选项

联方单层球面网壳环杆采用Φ168 mm×5 mm，斜杆采用Φ146 mm×5 mm，跨度为50 m，矢跨比1/5，屋面荷载1.0 kN/m2，支承条件为固定铰支座，冲击体为圆柱体，采用改变材料密度的方法来改变冲击体质量.

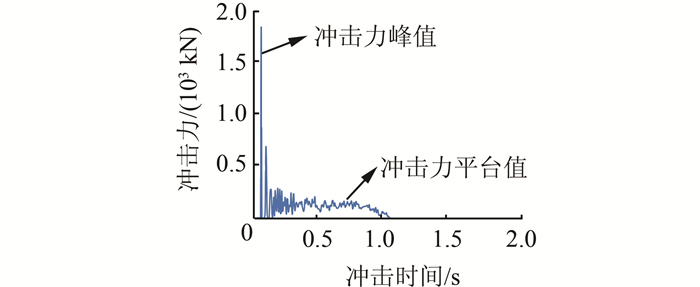
2 计算结果分析 2.1 网壳冲击力时程曲线

通过改变冲击体的质量和初始速度对网壳模型进行冲击，得到网壳在不同重量和速度冲击作用下的冲击力时程曲线，以下仅列出网壳两种典型冲击力时程曲线，如图 2、3所示.

图 2 网壳冲击力时程曲线(m=10 t、v=10 m/s) Figure 2 Time history curve of impact force (m=10 t、v=10 m/s) of dome
图选项
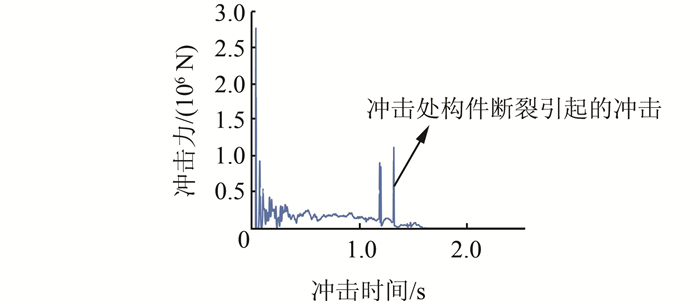
图 3 网壳冲击力时程曲线(m=15 t、v=15 m/s) Figure 3 Time history curve of impact force (m=15 t、v=15 m/s) of dome
图选项

通过对模型在不同冲击速度和重量作用下冲击力时程曲线的分析，可知通常冲击过程在2 s以内完成，并且从图 2可以明显看出冲击力时程曲线可以分为3段：第1阶段为冲击阶段；第2阶段为稳定相持阶段；第3阶段为衰减阶段.

随着冲击速度和冲击重量的增加，冲击阶段的冲击力峰值也增加，但稳定相持阶段的冲击力平台值却基本保持不变，同时冲击力平台值持续的时间相应增加.

由图 3可以看出，冲击力时程曲线在稳定相持阶段的末段冲击力发生突然变化，这是由于冲击过程中冲击处的杆件突然断裂导致冲击力发生突然变化.

2.2 弦支结构冲击力时程曲线

弦支网壳的冲击性能通过在不同索力、冲击速度和冲击重量作用下模型的冲击，得到在各种条件下弦支结构的冲击力时程曲线.以下仅列出弦支结构典型的冲击力时程曲线，如图 4~6所示.

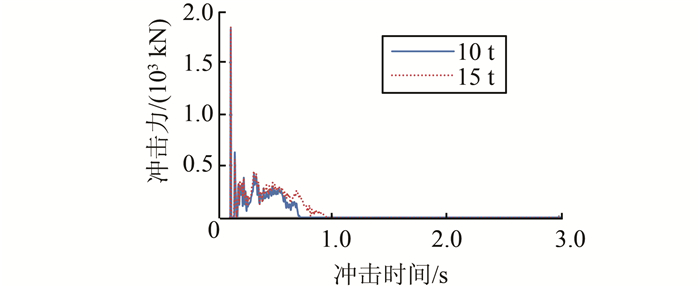
图 4 冲击力时程曲线(m=5 t、v=10 m/s) Figure 4 Time history curve of impact force (m=5 t、v=10 m/s) of dome
图选项
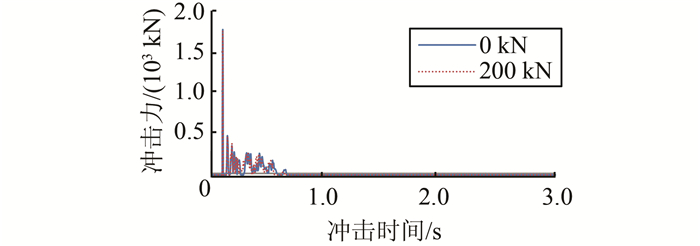
图 5 冲击力时程曲线(m=10 t、f=200 kN) Figure 5 Time history curve of impact force (m=10 t、f=200 kN) of dome
图选项
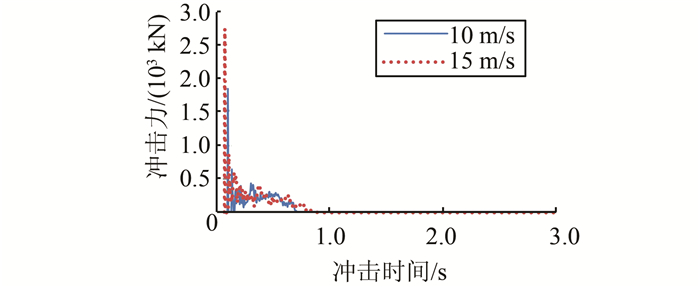
图 6 冲击力时程曲线(v=10 m/s、f=200 kN) Figure 6 Time history curve of impact force(v=10 m/s、f=200 kN) of dome
图选项

从图 4可以看出，在相同的冲击速度和冲击重量的作用下，弦支结构的冲击力时程曲线随着索力的增加冲击力峰值和冲击力平台值基本没有变化.弦支网壳的冲击力峰值相对于单层网壳而言基本没变化，这是由于冲击力峰值与网壳的局部刚度有关，弦支并没有改变网壳的局部刚度，因此冲击力峰值不会发生较大的变化.但由于弦支和索的作用使网壳的整体刚度增加从而冲击力平台值有所增加，并且弦支网壳的冲击时间相对单层网壳有所减小，这是由于弦支增加了网壳的整体刚度故冲击力平台值有所增加，弦支网壳与单层网壳相比呈现出一定的刚性.

从图 5可看出，在相同的索力和冲击重量的作用下，弦支结构的冲击力时程曲线随着冲击速度的增加冲击力峰值也增加，冲击力平台值变化不大，这是由于在索力相同的条件下，弦支网壳的局部和整体的刚度不会发生变化，故冲击力平台值不会随着冲击速度的增加而增加.与冲击力平台值相比，冲击力峰值随速度变化而变化的量更大，即冲击力峰值对速度变化更为敏感.冲击时间随着冲击速度的增加而增加.

从图 6可以看出，在相同的索力和冲击速度的作用下，弦支结构的冲击力时程曲线随着冲击重量的增加冲击力峰值略有增加，冲击力平台值变化不大，即冲击力峰值和冲击力平台值对冲击物重量的变化不是很敏感.冲击时间随着冲击重量的增加而增加.

2.3 网壳冲击位移时程曲线

通过改变冲击体的质量和初始速度对同一网壳模型进行了冲击，从而得到了网壳在不同重量和速度冲击作用下的位移时程曲线，以下仅列出部分位移时程曲线，如图 7、8所示.

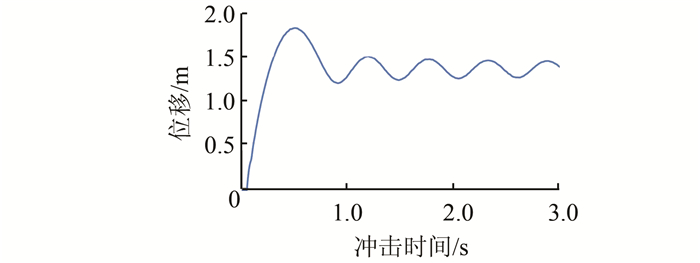
图 7 位移时程曲线(m=5 t、v=10 m/s) Figure 7 Time history curve of displacement (m=5 t、v=10 m/s)
图选项
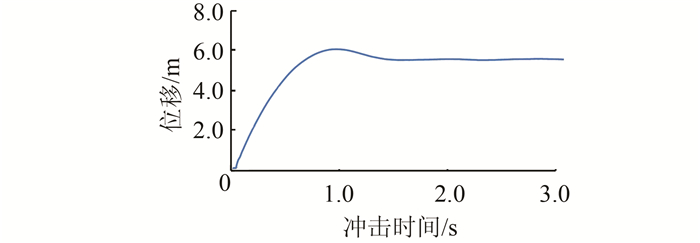
图 8 位移时程曲线(m=10 t、v=10 m/s) Figure 8 Time history curve of displacement (m=10 t、v=10 m/s)
图选项

从图 7、8可以看出，随着冲击重量和冲击速度的增加，网壳的最大位移和冲击时间增加；冲击结束后网壳自由振动的振幅和频率随着冲击重量和冲击速度的增加将逐渐减小.

2.4 弦支结构冲击位移时程曲线

通过对在不同索力、冲击速度和冲击重量作用下的弦支结构模型的冲击模拟，得到在各种条件下的位移时程曲线，以下仅列出了部分冲击力时程曲线，如图 9~11所示.

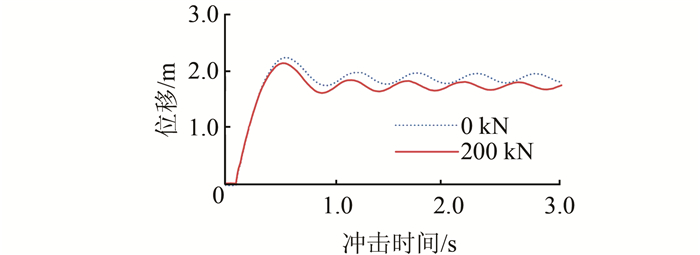
图 9 位移时程曲线(m=10 t、v=10 m/s) Figure 9 Time history curve of displacement (m=10 t、v=10 m/s)
图选项
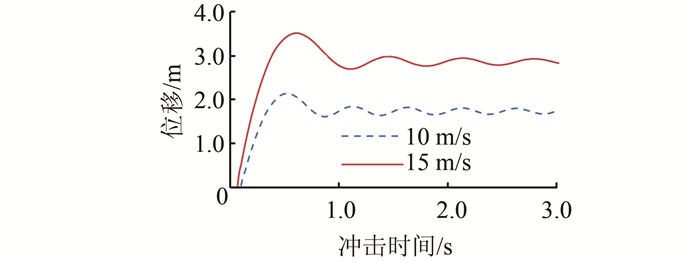
图 10 位移时程曲线(m=10 t、f=200 kN) Figure 10 Time history curve of displacement (m=10 t、f=200 kN)
图选项
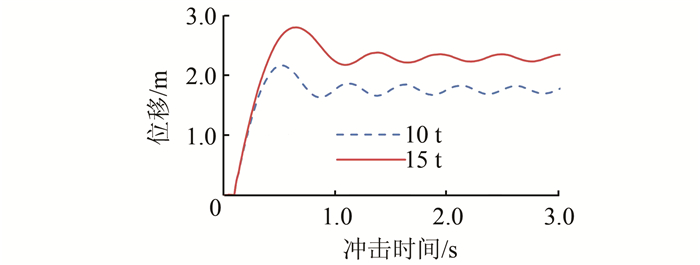
图 11 位移时程曲线(v=10 m/s、f=200 kN) Figure 11 Time history curve of displacement (v=10 m/s、f=200 kN)
图选项

在相同的冲击速度和冲击重量的作用下，弦支结构随着索力的增加最大位移会略有减小，但变化不大，也即弦支结构本身增加索力无法显著减小冲击荷载作用下的位移；但弦支结构与相应的单层网壳相比，加弦支可增加弦支结构本身刚度，在相同的冲击速度和冲击重量的作用下，可显著减小网壳的最大位移，增加网壳的抗冲击能力.

在相同的索力作用下，弦支结构的最大位移随着冲击速度和冲击重量的增加而增加，冲击结束后的自由振动频率随着冲击速度的增加而减小.

2.5 径向杆件应力

网壳径向杆件的冲击应力变化，如图 12所示.

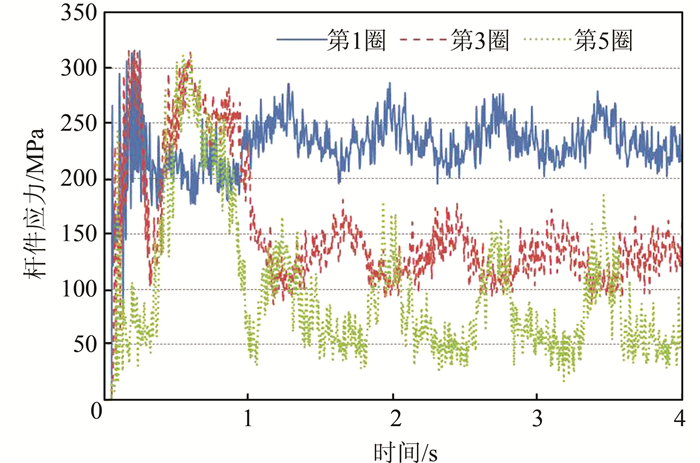
图 12 径向杆件应力的变化 Figure 12 Changes of radial bar stress
图选项

从图 12可知:第1圈、第3圈径向杆件冲击应力基本同步达到峰值，第5圈径向杆件冲击应力达到峰值比第1圈和第3圈滞后一点；第1圈杆件直接受到冲击变形较大，因此残余应力也最大.从上述分析可知，径向杆件的冲击应力距离冲击点越远，冲击应力峰值及残余应力越小.

2.6 环向杆件的应力

网壳环向杆件的冲击应力变化如图 13所示.

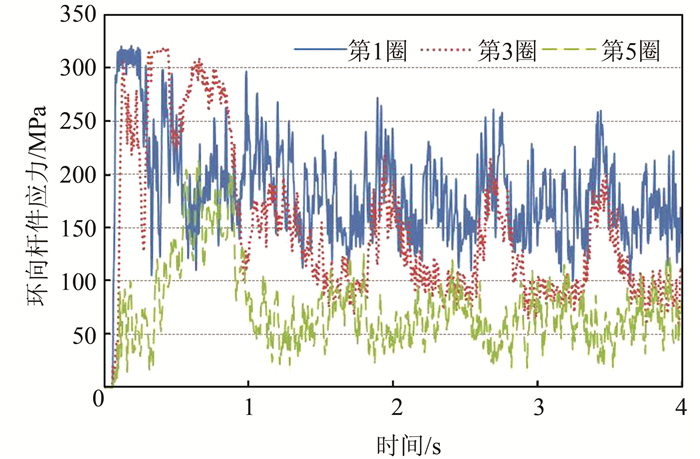
图 13 径向杆件应力的变化 Figure 13 Changes of ring bar stress
图选项

从图 13可知，环向杆件的冲击应力从冲击点处由内环向外环杆逐步达到峰值，第一圈环向杆件受到冲击变形较大，因此残余应力也最大.从上述分析可知，径向杆件的冲击应力距离冲击点越远冲击应力峰值及残余应力也逐渐减小.

弦支结构的径向和环向杆件也和网壳一样有相同的规律.

3 结论

1) 联方单层网壳及其弦支结构具有类似冲击过程，冲击力时程曲线可分为3阶段.

2) 弦支结构相对于单层网壳而言具有较强的抗冲击能量.弦支结构索力的增加对弦支结构本身提高抵抗冲击的能力有限.

3) 单层网壳及相应的弦支结构的径向和环向杆件冲击应力具有相同的变化规律.

参考文献
[1] 陈志华, 刘红波, 王小盾. 弦支穹顶结构研究综述[J]. 建筑结构学报, 2010(增刊1): 210–215.
Chen Zhihua, Liu Hongbo, Wang Xiaodun. Review and forecast of suspendome structures[J]. Journal of Building Structures, 2010(Sup.1): 210–215.
[2] 史俊亮. K8型单层网壳在冲击荷载作用下的动力响应研究[D]. 太原: 太原理工大学, 2005.
Shi Junliang. Dynamic response research on K8 single-layer reticulated dome under impact[D]. Taiyuan: Taiyuan University of Technology, 2005. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y788423
[3] 尚晓江, 苏建宇, 王化峰, 等. ANSYS/LS-DYNA动力分析方法与工程实例[M]. 北京: 中国水利水电出版社, 2008: 162-171.
Shang Xiaojiang, Su Jianyu, Wang Huafeng, et al. Analysis and Engineering Application of ANSYS/LS-DYAN[M]. Beijing: China Water & Power Press, 2008: 162-171.
[4] Samuel Tan. Cable based retrofit of steel building floors to prevent progressive collapse[D]. University of California in Berkeley, 2003.
[5] 陆新征, 江见鲸. 世界贸易中心飞机撞击后倒塌过程的仿真分析[J]. 土木工程学报, 2001, 34(6): 8–10.
Lu Xinzheng, Jiang Jianjing. Dynamic finite element simulation for the collapse of World Trade Center[J]. China Civil Engineering Journal, 2001, 34(6): 8–10.
[6] 王多智, 范峰, 支旭东, 等. 考虑重力效应的单层球面网壳抗冲击荷载性能[J]. 哈尔滨工业大学学报, 2009, 41(8): 19–23.
Wang Duozhi, Fan Feng, Zhi Xudong, et al. Performance of single-layer reticulated domes under impact load and gravity[J]. Journal of Harbin Institute of Technology, 2009, 41(8): 19–23.
[7] Zheng Liang, Chen Zhihua. Finite element analysis of a single-layer reticulated dome under impact loading[J]. Advanced Materials Research, 2011, 163: 327–331.
[8] Karagiozova D, Alves M. Transition from progressive buckling to global bending of circular shells under axial impact Part Ⅰ:Experimental and numerical observations[J]. International Journal of Solids and Structures, 2004, 41(5-6): 1565–1580. DOI:10.1016/j.ijsolstr.2003.10.005
[9] Karagiozova D, Alves M. Transition from progressive buckling to global bending of circular shells under axial impact Part Ⅱ: Theoretical analysis[J]. International Journal of So1ids and Structures, 2004, 41(5-6): 1581–1604. DOI:10.1016/j.ijsolstr.2003.10.006
[10] 王多智, 支旭东, 范峰, 沈世钊. 冲击荷载下K8单层球面网壳的破坏类型[J]. 工程力学, 2008, 25(Suppl Ⅱ): 144–149.
Wang Duozhi, Zhi Xudong, Fan Feng, Shen Shizhao. Failure patterns of Kiewitt8 single-layer reticulated domes under impact loads[J]. Engineering Mechanics, 2008, 25(Suppl Ⅱ): 144–149.
[11] 王多智, 范峰, 支旭东, 等. 单层球面网壳冲击试验研究[J]. 建筑结构学报, 2011, 32(8): 34–41.
Wang Duozhi, Fan Feng, Zhi Xudong, et al. Experimental study on single-layer reticulated dome under impact[J]. Journal of Building Structures, 2011, 32(8): 34–41.
[12] 赵振东, 钟江荣, 余世舟. 钢混结构物受外来飞射体冲击的破坏效应研究[J]. 地震工程与工程振动, 2003, 23(5): 89–94.
Zhao Zhendong, Zhong Jiangrong, Yu Shizhou. Study on damage to reinforced concrete structures by impacting of an aircraft[J]. Earthquake Engineering and Engineering Vibration, 2003, 23(5): 89–94.
[13] 刘锋, 吕西林. 冲击载荷作用下框架结构的非线性动力响应[J]. 振动工程学报, 2008, 21(2): 107–114.
Liu Feng, Lü Xilin. Nonlinear dynamic responses of impulsive loaded frame structure[J]. Journal of Vibration Engineering, 2008, 21(2): 107–114.
[14] 李海旺, 郭可, 魏剑伟, 等. 冲击载荷作用下单层球面网壳动力响应模型实验研究[J]. 爆炸与冲击, 2006, 26(1): 39–45.
Li Haiwang, Guo Ke, Wei Jianwei, et al. The dynamic response of a single-layer reticulated shell to drop hammer impact[J]. Explosion and Shock Waves, 2006, 26(1): 39–45. DOI:10.11883/1001-1455(2006)01-0039-07