文章信息
- 柯璐, 李传习, 刘永明, 陈卓异, 林继乔
- KE Lu, LI Chuanxi, LIU Yongming, CHEN Zhuoyi, LIN Jiqiao
- 钢箱梁横隔板-U肋交接部位疲劳应力有限元分析
- FEA for fatigue stress of diaphragm-U rib connection in steel box girder
- 武汉大学学报(工学版), 2018, 51(2): 132-138, 177
- Engineering Journal of Wuhan University, 2018, 51(2): 132-138, 177
- http://dx.doi.org/10.14188/j.1671-8844.2018-02-006
-
文章历史
- 收稿日期: 2017-01-05
2. 亚利桑那州立大学,坦陂 85281;
3. 佛山市路桥建设有限公司,广东 佛山 528303
2. Arizona State University, Tempe 85281, USA;
3. Foshan Road & Bridge Construction Co., Ltd., Foshan 528303, China
正交异性钢箱梁广泛应用于国内外大中型桥梁建设,但是其桥面板疲劳开裂一直是桥梁工程界的一大世界性难题[1-3].当前国内外学者进行钢结构疲劳研究的常用方法包括数值模拟和模型试验[3-6],两种方法各有优势,互为补充.钢箱梁的疲劳实际是轮载"局部效应"下构造细节的塑性损伤累积,构造细节应力计算是疲劳分析的关键.有限元法能够准确计算正交异性桥面板复杂构造的畸变应力与位移,能够很好地适应复杂结构疲劳分析的需要,省去了模型试验大量的人力和物力投入,因而被广泛应用[3, 6, 7].由于预测疲劳寿命与结构疲劳应力幅的3~5次方成正比[8],因此采用科学的方法准确计算疲劳应力,对于准确地进行结构疲劳检算与寿命预测具有重要意义.
钢箱梁的疲劳大致分为两类:一类为焊接接头的疲劳,常用分析方法为热点应力法[6, 9-12];另一类为桥面板、U肋、横隔板等钢板母材的疲劳,多采用名义应力法[13, 14].热点应力计算方面,周张义与李芾[9]提出网格精细应考虑焊趾附近一定的结构范围,并能反映焊趾处面内与面外弯曲引起的高应力梯度.韩冰[11]以及狄生奎[12]等采用ANSYS软件建模,比较了单元类型和外推方法对焊趾热点应力的影响,探讨了热点应力的计算精度问题,但仅基于ANSYS平台及其相应单元类型.Aygül等[15]基于ABAQUS软件,比较了实体单元和板单元不同建模方式、不同网格精度对纵肋与横隔板焊缝热点应力的影响,但未关注单元类型的影响.钢箱梁横隔板弧形切口构造变化剧烈,切口形状极不规则,对于该部位局部应力的有限元分析,相关研究较少.本文基于ABAQUS平台,分别建立了钢箱梁体壳混合单元模型(模型Ⅰ)和纯板壳单元有限元模型(模型Ⅱ),基于模型Ⅰ比较了单元类型、网格精度及外推方法对U肋-横隔板焊缝尾端(围焊)计算热点应力的影响,基于模型Ⅰ与模型Ⅱ比较了单元类型和网格尺寸对横隔板弧形切口局部应力分布的影响,得到了基于ABAQUS平台进行钢箱梁焊接及非焊接细节疲劳应力分析的基本方法,可为相关研究提供参考.
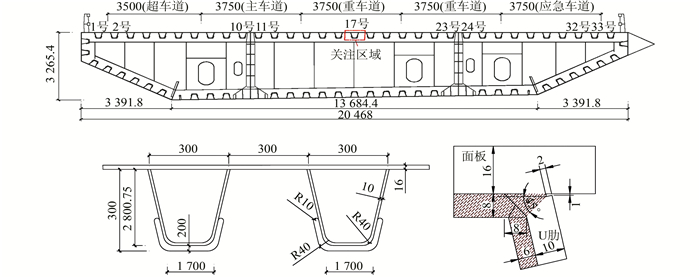
1 有限元模型某悬索桥钢箱梁标准断面以及构造细节尺寸如图 1所示,选取远离钢箱梁纵隔板的顶板17号U肋与横隔板交接部位为关注区域.
|
| 图 1 钢箱梁标准断面及构造细节尺寸(单位:mm) Figure 1 Standard section of steel box girder and basic size of structural details(unit: mm) |
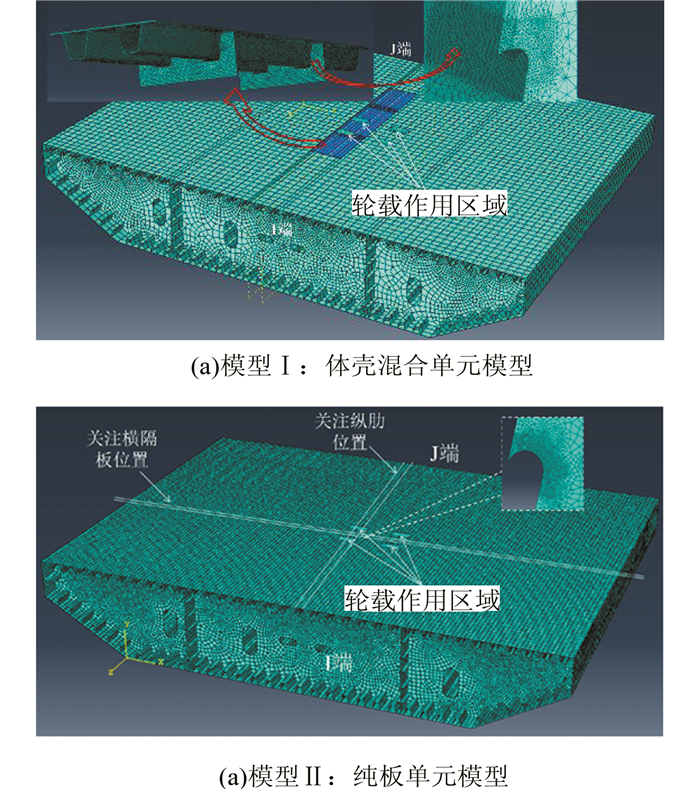
利用有限元软件ABAQUS V6.14-3,分别建立钢箱梁体壳混合单元模型(模型Ⅰ)和纯板单元模型(模型Ⅱ)进行疲劳应力分析,有限元模型如图 2所示.模型Ⅰ全局采用板单元模拟,而横隔板-U肋交叉部位及其附近采用体单元模拟,严格模拟焊缝构造.模型Ⅱ全部采用板单元,不模拟焊缝构造.两模型纵向均考虑4个横隔板间距的节段长度(4×3 m=12 m),横向取全桥宽度.桥面板疲劳受桥梁整体受力影响很小[2],依据圣维南原理,远离关注部位的结构边界条件对关注部位受力影响很小,钢箱梁I端约束其横隔板下缘节点3个方向平动自由度,J端约束横隔板下缘节点竖向、横桥向方向平动自由度.两模型总体网格尺寸取150 mm,关注区域网格细化,网格尺寸逐步连续过渡.钢材采用Q345qC,弹性模量为2.06×105 MPa,泊松比为0.3.
|
| 图 2 箱梁节段有限元模型 Figure 2 Finite element model of steel box girder segment |
对于焊接接头热点应力分析、焊缝区域采用板单元涉及焊缝模拟与否、应力取值是否排除焊缝尺寸等问题,本文仅利用模型Ⅰ进行分析(而体单元能准确模拟焊缝构造).对于横隔板弧形切口母材区域应力分析,板单元、体单元都可能具有较高的精度,利用模型Ⅰ与模型Ⅱ进行分析.
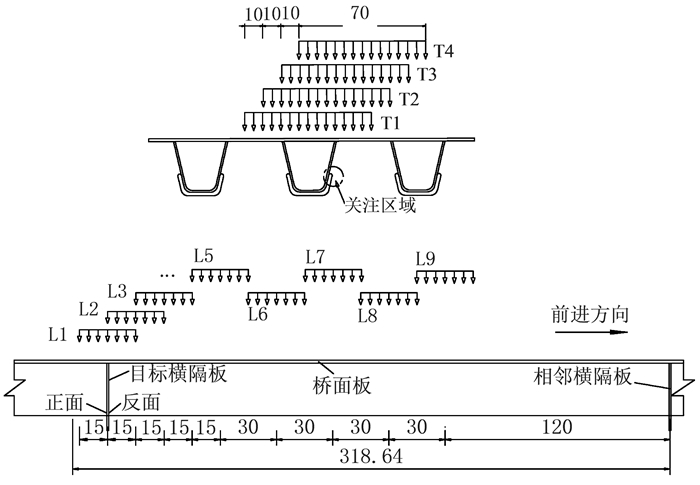
计算荷载依据《公路桥结桥梁设计规范JTG D64-2015》及Eurocode3(EC3)中的疲劳车辆模型Ⅲ确定,采用其后轴的120 kN+120 kN双联轴单独加载(即考虑4个轮载作用).单轮重为60 kN,横向轮距1.8 m,轴距1.2 m,考虑5 cm铺装层荷载扩散效应后单轮作用范围为0.7 m×0.3 m.以左前轮为参考轮,从计算位置正上方每次沿横向移动10 cm,即可得4个横向加载工况(T1~T4);纵向上从目标横隔板正上方以15 cm为间距移动4次,再以30 cm为间距移动4次,共得到9个纵向工况(L1~L9),车轮加载方式如图 3所示.
|
| 图 3 车轮荷载加载方式(单位:cm) Figure 3 Loading mode of wheel (unit:cm) |
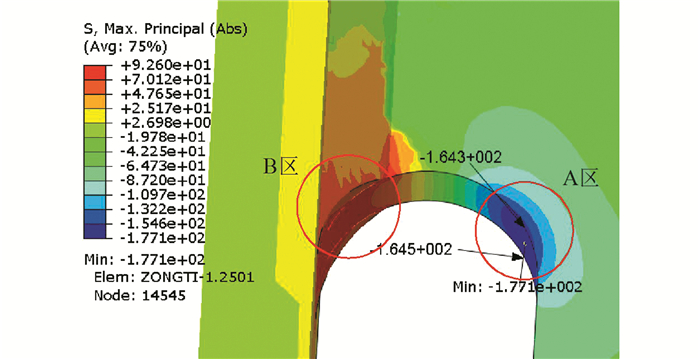
经试算,横隔板弧形切口最大主应力工况为T2-L5(工况Ⅰ,主要为面内变形),面外变形最大的工况为T2-L9(工况Ⅱ).计算结果表明,轮载作用下横隔板-U肋交接部位存在明显的压应力集中区(A区)和拉应力集中区(B区),如图 4所示.B区为焊接接头,A区为弧形切口钢板母材,分别采用热点应力和主应力作为疲劳控制参量.
|
| 图 4 横隔板-U肋交接部位主应力云图 Figure 4 Nephogram of principal stresses of diaphragm-U rib connection |
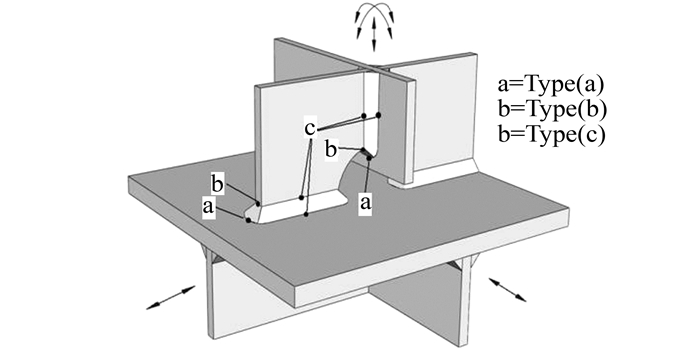
对于理想焊接接头,疲劳裂纹多萌生于焊趾前沿,正交异性桥面板中,一般有3种热点类型,如图 5所示,a类热点位于附板端部的主板表面,b类热点位于附板端面,c类热点位于主板与附板焊缝方向的主板或附板表面.
|
| 图 5 热点类型 Figure 5 Types of hot spots |
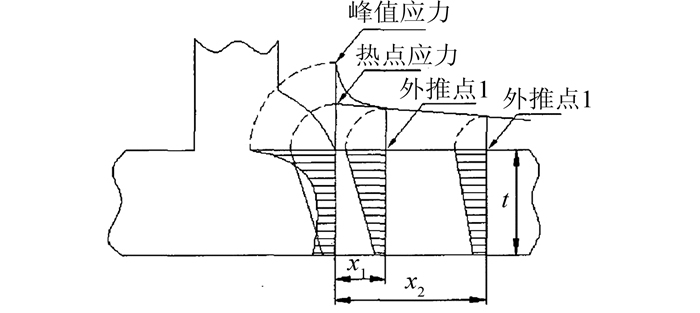
焊趾前沿局部总应力(切口应力)为膜应力、弯曲应力与焊趾引起的非线性应力的总和,热点应力为不计焊缝自身切口效应的构造局部峰值应力,也称"几何应力".计算热点应力时,需要采用一定的插值方法排除切口非线性应力,通常利用板件表面距离焊趾一定距离的两点处应力进行线性外推,或者利用三点应力进行二次外推.表面外推法计算原理如图 6所示.
|
| 图 6 表面外推法计算原理 Figure 6 Principle of surface extrapolation method |
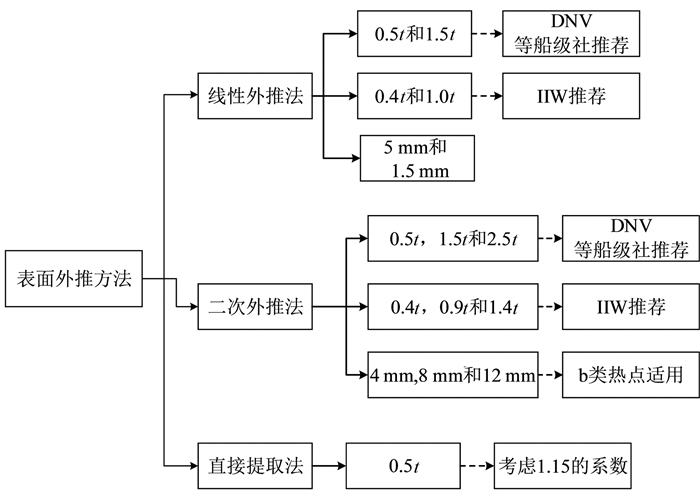
国内外船舶、机械和钢结构研究者提出了各种方法排除焊缝非线性应力,各船级社如挪威船级社(DNV)、中国船级社(CCS)以及国际焊接协会(IIW)等研究机构都有自己推荐的热点应力外推方法[9],常见的表面外推方法如图 7所示.图中,t为热点所在板件的厚度.
|
| 图 7 常用的表面外推方法 Figure 7 Common surface extrapolation methods |
IIW和许多船级社建议使用热点附近最大主应力作为热点应力法疲劳控制参量,且明确最大主应力方向与焊趾正向夹角θ为60°以内为宜,若超过60°,则采用垂直焊缝方向的正应力作为疲劳控制参量.
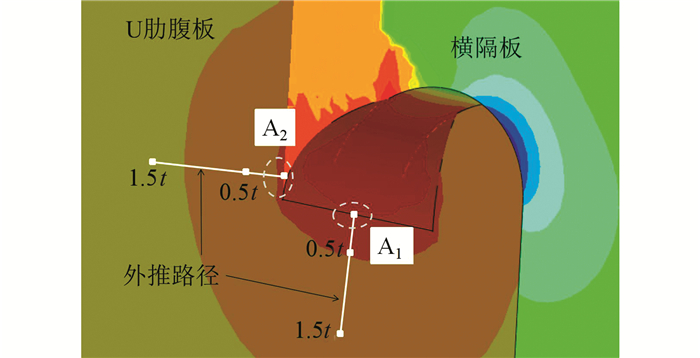
2.2 单元类型与网格尺寸对局部应力分布的影响采用模型Ⅰ进行热点应力分析,围焊处U肋腹板表面主应力最大工况为工况Ⅰ.以横隔板与U肋腹板围焊处A1与A2热点(分别为图 4所示a类与c类热点)作为研究对象,热点位置及应力取值路径如图 8所示.
|
| 图 8 热点位置与外推路径 Figure 8 Locations of hot spots and extrapolation paths |
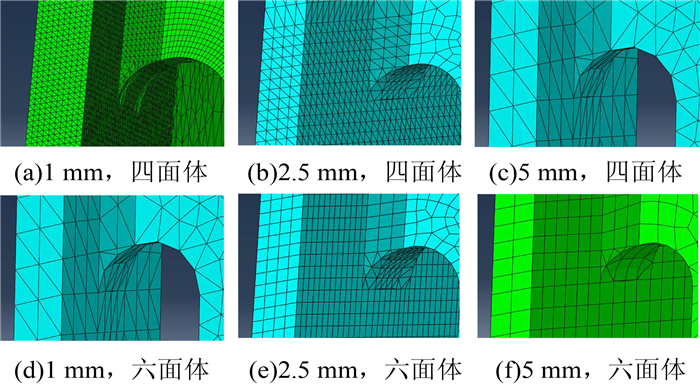
关注区域分别采用4节点一阶四面体单元(C3D4)、10节点二阶四面体单元(C3D10)、8节点一阶六面体单元(C3D8)和20节点二阶六面体单元(C3D20)进行模拟.网格划分精度分别取1 mm、2.5 mm和5 mm,单元划分情况如图 9所示.
|
| 图 9 单元类型与网格划分情况 Figure 9 Element types and meshing |
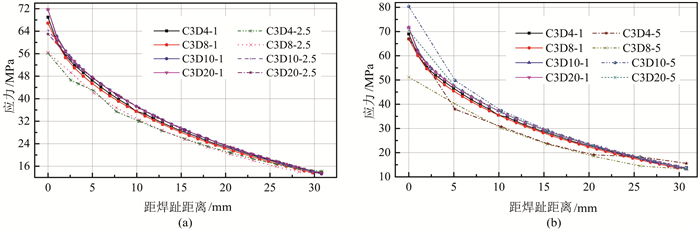
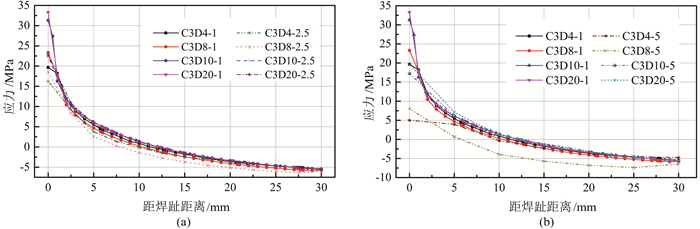
计算表明,热点A1处主拉应力与焊趾线基本垂直,取主应力作为疲劳参量,热点A2处最大与最小主应力方向与焊趾正方向夹角均超过60°,故A2热点的疲劳分析参量取焊趾正方向应力σz(沿桥纵向正应力).分别沿path1、path2(图 7)提取应力值,得到采用不同单元类型、不同网格精度时A1热点处沿path1、A2热点处沿path2的应力分布情况,如图 10~11所示.
|
| 图 10 热点A1处沿路径Path1应力分布情况 Figure 10 Stress distribution along Path1 of hot spot A1 |
|
| 图 11 热点A2处沿Path2应力分布情况 Figure 11 Stress distribution along Path2 of hot spot A2 |
结果表明,距焊趾5 mm(0.5t,t为板厚)以外应力分布基本呈线性变化,可见焊缝非线性应力的影响范围在距焊趾1/2板厚的范围内,为排除焊缝非线性应力,应力取值点应位于0.5t以外.相比于一阶单元,高阶单元得到的应力分布对网格尺寸的收敛性更好,两种高阶段单C3D10和C3D20计算结果差异很小.热点应力计算建议采用高阶四面体或六面体单元,网格尺寸划分至1/4板厚(2.5 mm),可达到较高的计算精度.若采用2.5 mm及以上网格尺寸,一阶单元C3D4和C3D8的计算精度较差,不建议采用.当划分网格足够精细(如单元细分至0.1t),不同单元均可达到计算精度要求,但计算耗时较长.
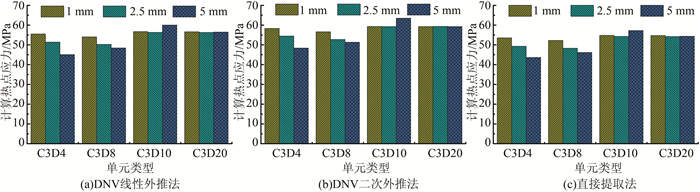
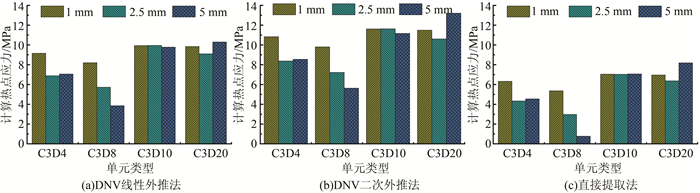
2.3 外推方法对热点应力的影响分别采用DNV线性外推、DNV二次外推以及直接提取法(0.5t处应力, 考虑1.15的系数),计算得到A1与A2热点应力,如图 12~13所示.结果表明,采用二次外推计算热点应力对网格尺寸收敛性较好,计算热点应力最大,疲劳检算结果将偏安全.采用直接提取法计算得到的热点应力结果离散性较大,相比于其他外推方法结果偏小,故不建议采用.单元类型对热点应力的影响显著大于网格尺寸,网格大小不超过0.25t时,采用C3D10和C3D20单元可达到较高的精度.A1热点与A2热点能得到基本一致的结论,可见上述结论对于a类与c类热点均适用.
|
| 图 12 A1处热点应力计算结果 Figure 12 Calculated values of hot spot stress of A1 |
|
| 图 13 A2处热点应力计算结果 Figure 13 Calculated values of hot spot stress of A2 |
有研究表明,过大的主压应力幅为弧形切口母材疲劳的原因[4, 14],也有观点认为,横隔板弧形切口的疲劳为板件面外变形所致[16],因此需对其最大主应力和最大面外应力两个工况进行分析.
3.1 单元类型与网格尺寸对主应力的影响利用模型Ⅰ和模型Ⅱ分析工况Ⅰ下的弧形切口疲劳应力.模型Ⅰ采用第2节相同的单元类型,模型Ⅱ分别采用以下4种单元建模:3节点通用有限应变板单元(S3)、4节点通用有限应变板单元(S4)、二阶6节点三角形薄板单元(STRI65,每个节点5自由度),以及二阶8节点厚板减缩积分单元(S8R).计算得到工况Ⅰ下弧形切口A区的主应力结果,见表 1~2.
| 网格尺寸/mm | 主应力/MPa | |||
| C3D4 | C3D8 | C3D10 | C3D20 | |
| 1.3 | -165.5(161.2) | -159.2(160.0) | -175.7(172.3) | -177.1(170.1) |
| 1.0 | -165.5(161.2) | -166.5(-165.4) | -176.0(172.3) | -176.1(172.4) |
| 注:括号外为第三主应力,括号内为Mises应力. | ||||
| 网格尺寸/mm | 主应力/MPa | |||
| S3 | S4 | STRI65 | S8R | |
| 0.5 | -153.0(149.4) | -171.8(167.6) | -167.9(167.4) | -166.8(166.7) |
| 0.3 | -157.1(153.7) | -172.0(169.7) | -171.3(170.8) | -169.3(168.2) |
| 注:括号外为第三主应力,括号内为Mises应力. | ||||
模型Ⅰ分析结果表明,相比于一阶实体单元,二阶实体单元具有更高的精度,对网格精度的要求也稍低,网格细分至1.3 mm结果即收敛.一阶单元计算主应力结果较二阶单元偏小,最大相差11.6%,不建议采用.模型Ⅱ分析结果表明,对于弧形切口母材高应力集中区,关注局部采用S4、STRI65和S8R,结果都具有较高的精度,网格尺寸从0.5 mm减小至0.3 mm,主压应力结果变化不超过3%,已基本收敛.一阶三节点板单元S3本身刚度过大,造成计算结果严重失真,应力集中部位应避免使用.
模型Ⅰ、Ⅱ结果对比分析表明,采用不同的单元、不同的网格,主应力计算结果最大相差24.6 MPa,相差16%,在二阶单元范围内,计算结果最大相差10.8 MPa,相差6.5%,二阶单元结果离散性明显缩小.另外,板单元计算结果较体单元普遍偏小.结构疲劳寿命与疲劳应力幅的3~5次方成正比,精确的疲劳应力分析对于准确预测结构寿命非常重要,建议采用精度更高的二阶体单元.
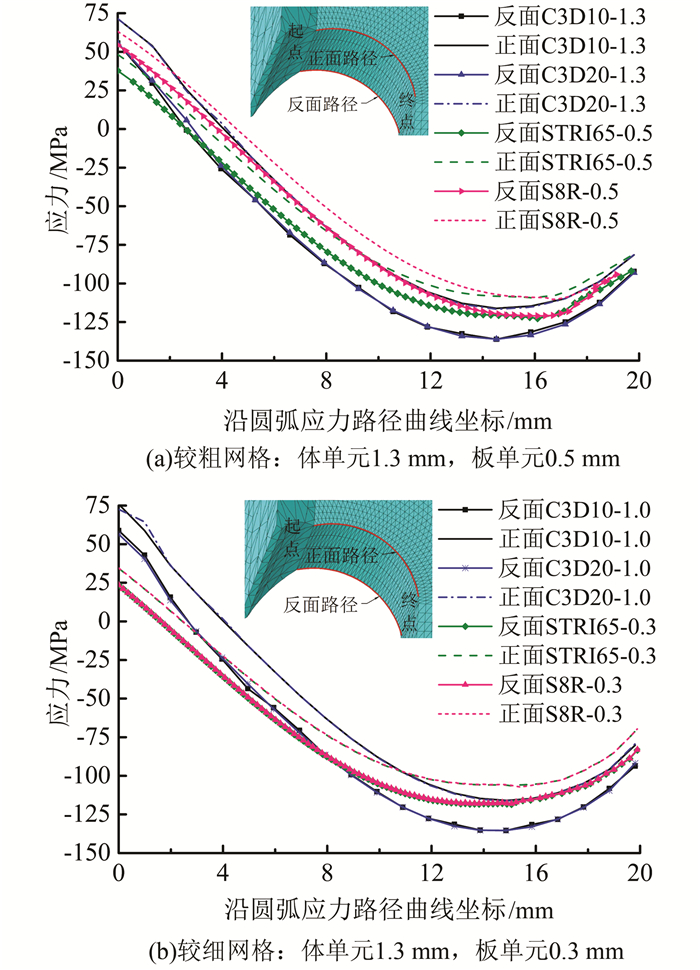
3.2 单元类型和网格尺寸对面外应力的影响由上文分析可知,采用二阶单元分析横隔板弧形切口应力,精度和收敛性明显优于一阶单元,本节仅对二阶单元进行讨论.模型Ⅰ和模型Ⅱ按工况Ⅱ进行加载,得到不同单元、不同网格尺寸下弧形切口母材正面与反面(如图 3,远离参考轮侧为正面,邻近参考轮侧为反面)应力分布如图 14所示,应力峰值汇总于表 3~4.
|
| 图 14 采用不同单元类型与网格尺寸时正反面应力分布 Figure 14 Stress distribution on the positive and negative sides versus different element types and mesh sizes |
| 网格尺寸/mm | 应力峰值/MPa | |
| C3D10 | C3D20 | |
| 1.3 | -136.2/-116.1(20.1) | -136.1/-116.6(19.5) |
| 1.0 | -135.5/-115.9(19.6) | -135.4/-116.3(19.1) |
| 注:第1~2个数据依次为反面与正面主应力峰值,括号内为两者差值,即面外应力. | ||
| 网格尺寸/mm | 应力峰值/MPa | |
| STRI65 | S8R | |
| 0.5 | -122.7/-109.4(13.3) | -121.0/-110.4(10.6) |
| 0.3 | -118.2/-106.4(11.8) | -118.1/-107.3(10.8) |
| 注:第1~2个数据依次为反面与正面主应力峰值,括号内为两者差值,即面外应力. | ||
结果表明,体单元与板单元计算的正反面应力分布差异较大,板单元计算的弧形切口正、反面主应力峰值及面外应力均偏小.体单元网格划分为1.3 mm时结果收敛,板单元划分至0.3 mm时结果才收敛.二阶体单元能准确模拟板厚方向的非线性应力分布,当板件面外变形较为显著且为研究关注对象时,宜采用二阶实体单元.一般认为厚度与长度之比在1/20~1/10之间的板壳,应考虑剪切变形的影响,中面的法线不再垂直板中面的挠曲线,不宜采用基于柯西霍夫假设的薄板单元,本文分析表明,在网格足够精细(0.3 mm及以下)时,薄板单元STRI65与厚板单元S8R计算结果基本一致.
4 结论1) 对于钢箱梁焊接接头的热点应力计算,二阶体单元计算精度显著优于一阶体单元,且二阶单元对于网格尺寸的收敛性较好,采用二阶四面体单元C3D10和二阶六面体单元C3D20计算结果差异很小,单元划分至t/4(t为板厚)即可.
2) 横隔板-U肋腹板焊缝围焊处,焊缝切口非线性应力影响在距焊趾0.5t范围以内,0.5t以外应力基本呈线性分布,为排除焊缝非线性应力,表面外推应力取值点应位于0.5t以外.DNV等推荐的二次外推方法得到的热点应力离散性较小,热点应力值最大,建议采用该法进行热点应力计算.该结论对于a类、c类热点均适用.
3) 对于弧形切口母材疲劳应力分析,为确保计算精度,建议采用精度更高的二阶体单元进行结构模拟,单元应划分至1.3 mm.板单元结果相比于体单元普遍偏小,若采用板单元,网格应划分至0.3 mm以下.一阶3节点板单元S3本身刚度过大,计算结果严重失真,应力集中部位应避免使用.
4) 进行弧形切口面外应力分析时,在二阶单元范围内,板单元与实体单元得到的正反面应力分布差异较大,板单元计算的切口正、反面应力峰值及面外应力均偏小,偏不安全.二阶体单元能够准确模拟板厚方向的非线性应力分布,当板件面外变形显著且为研究关注对象时,应采用二阶实体单元.
| [1] |
吕彭民, 李大涛. 正交异性钢桥面板顶板疲劳性能研究[J].
中国公路学报, 2014(2): 84–89.
Lü Pengmin, Li Datao. Fatigue research on bridge deck-plate of orthotropic steel bridge deck[J]. China Journal of Highway and Transport, 2014(2): 84–89. |
| [2] | Shao Xudong, Yi Dutao, Huang Zhengyu, et al. Basic performance of the composite deck system composed of orthotropic steel deck and ultrathin RPC layer[J]. Journal of Bridge Engineering, 2013, 18(5): 417–428. DOI:10.1061/(ASCE)BE.1943-5592.0000348 |
| [3] | Wang B. Fatigue assessment of the diaphragm-to-rib welded connection in orthotropic steel deck using effective notch stress approach[J]. Journal of Failure Analysis and Prevention, 2015, 15(1): 65–73. DOI:10.1007/s11668-014-9909-0 |
| [4] |
唐亮, 黄李骥, 刘高, 等. 正交异性钢桥面板足尺模型疲劳试验[J].
土木工程学报, 2014(3): 112–122.
Tang Liang, Huang Liji, Liu Gao, et al. Fatigue experimental study of a full-scale steel orthotropic deck model[J]. China Civil Engineering Journal, 2014(3): 112–122. |
| [5] | Zhang Q, Cui C, Bu Y, et al. Fatigue tests and fatigue assessment approaches for rib-to-diaphragm in steel orthotropic decks[J]. Journal of Constructional Steel Research, 2015, 114: 110–118. DOI:10.1016/j.jcsr.2015.07.014 |
| [6] | Liu R, Liu Y, Ji B, et al. Hot spot stress analysis on rib-deck welded joint in orthotropic steel decks[J]. Journal of Constructional Steel Research, 2014, 97: 1–9. DOI:10.1016/j.jcsr.2014.01.012 |
| [7] | Zhang Q, Cui C, Bu Y, et al. Fatigue tests and fatigue assessment approaches for rib-to-diaphragm in steel orthotropic decks[J]. Journal of Constructional Steel Research, 2015, 114: 110–118. DOI:10.1016/j.jcsr.2015.07.014 |
| [8] | BS EN 1993-1-9: 2005, Eurocode 3: Design of Steel Structures-Part 1-9: Fatigue[S]. |
| [9] |
周张义, 李芾. 基于表面外推的热点应力法平板焊趾疲劳分析研究[J].
铁道学报, 2009(5): 90–96.
Zhou Zhangyi, Li Fu. Study on fatigue analysis of welded toes of plate structures using hot spot stress method based on surface extrapolation[J]. Journal of the China Railway Society, 2009(5): 90–96. |
| [10] | Yang M, Ji B, Yuanzhou Z, et al. Fatigue behavior and strength evaluation of vertical stiffener welded joint in orthotropic steel decks[J]. Engineering Failure Analysis, 2016, 70: 222–236. DOI:10.1016/j.engfailanal.2016.05.001 |
| [11] |
韩冰, 蒲黔辉, 施洲, 等. 桥梁正交异性板焊接构造热点应力计算方法研究[J].
桥梁建设, 2015(1): 56–61.
Han Bing, Pu Qianhui, Shi Zhou, et al. Study of calculation methods for hot spot stress of welded structure of bridge orthotropic plate[J]. Bridge Construction, 2015(1): 56–61. |
| [12] |
狄生奎, 文铖, 叶肖伟. 正交异性钢桥面板结构热点应力有限元分析[J].
浙江大学学报(工学版), 2015(2): 225–231.
Di Shengkui, Wen Chen, Ye Xiaowei. Finite element analysis of structural hot-spot stress for orthotropic steel bridge deck[J]. Journal of Zhejiang University (Engineering Science Edition), 2015(2): 225–231. |
| [13] |
李立峰, 张东波, 袁卓亚, 等. 正交异性钢桥面板中弧形缺口的受力分析[J].
公路交通科技, 2012(4): 55–61.
Li Lifeng, Zhang Dongbo, Yuan Zhuoya, et al. Stress analysis of arc-shaped cutouts in steel orthotropic deck plates[J]. Journal of Highway and Transportation Research and Development, 2012(4): 55–61. |
| [14] |
陈卓异, 李传习, 柯璐, 等. 某悬索桥钢箱梁疲劳病害及处治方法研究[J].
土木工程学报, 2017(3): 91–100.
Chen Zhuoyi, Li Chuanxi, Ke Lu, et al. Study on fatigue damages and retrofit methods of steel box girder in a suspension bridge[J]. China Civil Engineering Journal, 2017(3): 91–100. |
| [15] | Aygül M, Al-Emrani M, Urushadze S. Modelling and fatigue life assessment of orthotropic bridge deck details using FEM[J]. International Journal of Fatigue, 2012, 40: 129–142. DOI:10.1016/j.ijfatigue.2011.12.015 |
| [16] |
曾志斌. 正交异性钢桥面板典型疲劳裂纹分类及其原因分析[J].
钢结构, 2011(2): 9–15.
Zeng Zhibin. Classification and reasons of typical fatigue cracks in orthotropic steel deck[J]. Steel Structure, 2011(2): 9–15. |
 2018, Vol. 51
2018, Vol. 51



