文章信息
- 杨志炎, 程永光, 夏林生, 尤建锋
- YANG Zhiyan, CHENG Yongguang, XIA Linsheng, YOU Jianfeng
- 灯泡式水轮机甩负荷过渡过程三维数值模拟
- 3D numerical simulation of load rejection transients of a bulb hydraulic turbine
- 武汉大学学报(工学版), 2018, 51(10): 854-860, 875
- Engineering Journal of Wuhan University, 2018, 51(10): 854-860, 875
- http://dx.doi.org/10.14188/j.1671-8844.2018-10-002
-
文章历史
- 收稿日期: 2017-10-15
当前,低水头水力资源开发进度加快,灯泡式水轮机因其过流量大、效率高而被普遍应用.当机组甩负荷时,水锤惯性力、动静干涉及尾水涡带会引起机组振动,严重时会威胁电站安全.目前过渡过程研究主要采用一维方法,而灯泡式水轮机组流道短、直径大、三维尺度相当、水头低、重力场影响明显,用一维方法难以准确描述其特性[1-4].因此,三维模拟势在必行.
近年来,利用三维CFD技术对混流式和轴流式水轮机进行过渡过程研究已有较大突破,但对灯泡式水轮机的研究还鲜有报道[5-7].李金伟等[8]提出了转轮区域流动控制方程,模拟了混流式水轮机飞逸过渡过程,但该方法不能获得转轮运动的动态特性.周大庆等[9]提出了更新转轮区域网格运动速度的方法,模拟了轴流式水轮机飞逸过渡过程,结果与实验吻合较好.张晓曦等[10]利用FLOW-3D实现灯泡式水轮机三维过渡过程的模拟,但该软件不能生成贴体网格,计算结果欠精细.夏林生等[11]利用FLUENT,考虑重力场影响,分析了灯泡式水轮机飞逸过渡过程,解决了转轮加速问题,但飞逸过程导叶无运动.李师尧等[12]基于浸没边界法(Immersed Boundary Method)和Lattice Boltzmam Method耦合格式,首次尝试模拟了灯泡式水轮机内三维瞬变流问题,但此方法目前只能定性描述流态,难以精确定量计算.Yiming Li等[13]则利用FLUENT对灯泡式水轮机的启动和飞逸过程分别作了三维模拟,计算结果有很好的参考价值.
本文对灯泡式水轮机甩负荷过渡过程进行了三维模拟,通过动网格技术解决导叶运动问题,通过滑移网格模型控制转轮加速,并用上下水库模型保证重力场的准确性.
1 数值计算方法 1.1 计算模型和设定湍流模型:灯泡式水轮机体型复杂,表面曲率大,故选用处理大曲率流动效果较好的RNG k-ε湍流模型.
网格划分:使用ICEM软件划分混合网格.结构简单的水库和流道等部位采用结构化网格,网格质量高.空间扭曲的转轮、导叶等部位采用适应性强的四面体网格,经网格敏感性验证,网格数量定为285万.
数值解法:采用SIMPLEC算法,压力差值采用PRESTO方法.经多次比较,时间步长定为0.005 s,残差精度为10-4,每个时间步长最大迭代步数60步,确保网格更新中每个时间步都收敛.
边界条件:增加上水库和下水库两个计算区域,进口和出口设定压力边界条件,设置压力变化按照静水压强分布.
1.2 关键技术及解决方案灯泡式水轮机的导叶为空间曲面,模拟开度变化时,需设定每片导叶旋转轴并给出角速度的变化过程.另外,转轮为变速旋转,需通过用户自定义程序计算每个时间步的转速值,并逐步更新.
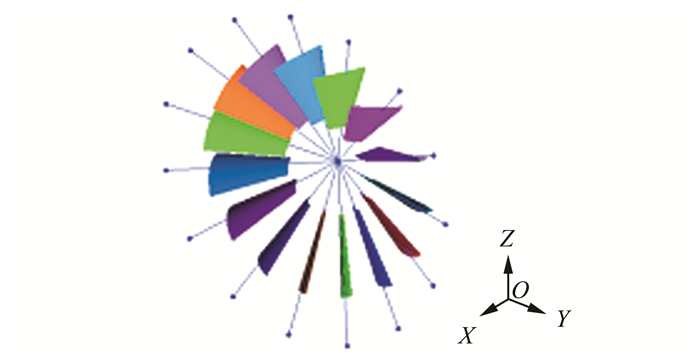
1.2.1 导叶运动规律设定导叶的所有旋转轴交于一中心点,如图 1.每片导叶绕轴旋转速度均可分解为X、Y和Z 3个方向上的旋转角速度,如图 2.由用户自定义程序给定各方向旋转速度,即可得每个导叶绕轴速度.
|
| 图 1 导叶与旋转轴 Fig. 1 Guide vanes and their rotating axes |
|
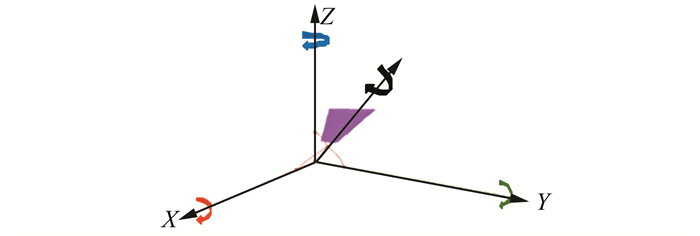
| 图 2 导叶转速分解 Fig. 2 Decomposition of guide vane rotating speed |
设定导叶旋转角速度为ω,以图 2导叶为例,旋转轴与X轴夹角为固定值θ0,则绕X轴旋转角速度为ωx=ω·cosθ0,ω在YZ平面的分速度为ωyz=ω·sinθ0,ωyz与Z轴的夹角在体型建立时给出,设定为θ,则ωz=ω·sinθ0·cosθ,ωy=ω·sinθ0·sinθ.
导叶总数为15片,相邻两根旋转轴在YZ平面投影的夹角为θ1,以X轴正方向为视角,以图 2导叶为起点,逆时针设定每片导叶旋转角速度:
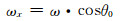 (1)
(1)
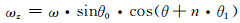 (2)
(2)
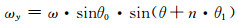 (3)
(3)
其中:n为导叶编号,n=1, 2, …, 14.
计算时采用动网格技术,按编号给定每片导叶的ωx、ωy和ωz,即可设定导叶运动规律.
1.2.2 甩负荷转轮加速设定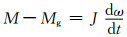 (4)
(4)
式中:M为水轮机动力矩;Mg为发电机阻力矩,包括机组发电输出力矩和损失力矩,甩全部负荷后,输出力矩为0,损失力矩可假定与转速平方成正比,按经验选取,对于灯泡式机组,损失力矩相对较小,此处忽略不计;J为整个发电机组的转动惯量,包括水体、转轮和发电机3部分.甩负荷过渡过程中,由于CFD计算时间步长很小,可采用一阶积分公式,将式(4)变化得ωi=ωi-1+Mi·Δt/J,以此来计算i+1时步角速度.计算过程中转轮转动区域采用滑移网格方法,便可实现甩负荷过渡过程模拟.
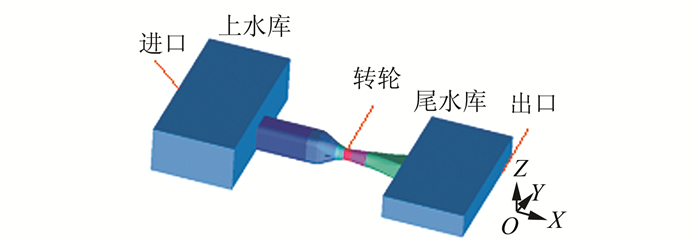
2 灯泡式水轮机甩负荷过渡过程三维模拟 2.1 计算条件水轮机基本参数:转轮直径5.3 m,活动导叶15片,转轮叶片3片,额定转速100 r/min,计算水头8 m,机组转动惯量为320 000 kg·m2.边界条件见图 3.
|
| 图 3 三维计算区域 Fig. 3 The 3D computational domain |
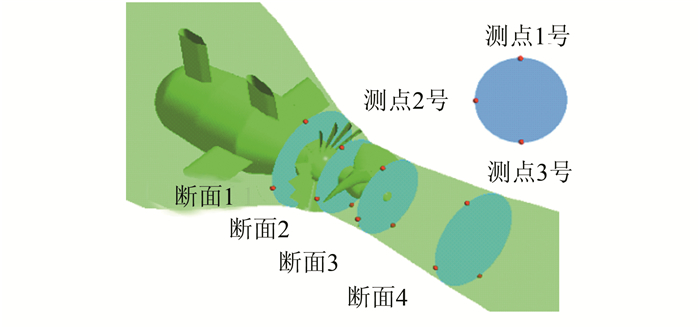
为监测过渡过程中水轮机流道内的压力脉动,在导叶上游、导叶与转轮之间、转轮出口、尾水管处设立4个监测面,每个监测面上按高度设立3个监测点,如图 4所示.
|
| 图 4 监测点布置图 Fig. 4 Layout of monitoring points |
导叶初始开度为70°,直线关闭至2.5°(动网格处理不能完全关闭),对关闭时间为7 s和13 s两种工况进行分析.
2.2 甩负荷过渡过程模拟结果 2.2.1 导叶7 s关闭1) 宏观参数分析
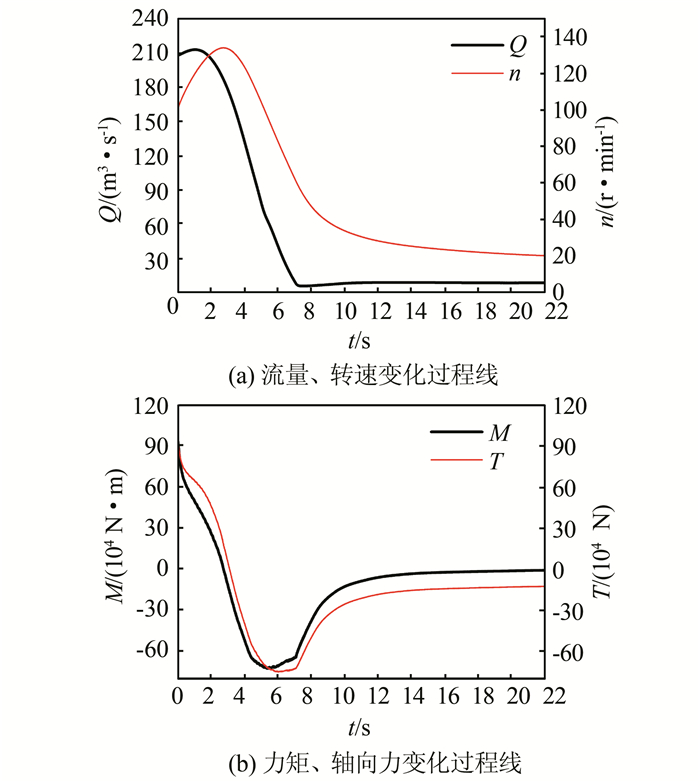
甩负荷后,水流做功使转速先上升到效率为0点后开始下降,流量变化也呈先上升后下降趋势,与灯泡式水轮机过流特性一致.转轮转速n、流量Q、转轮所受轴向力T和力矩M随时间变化见图 5.
|
| 图 5 甩负荷过程各宏观参数变化曲线(7 s导叶关闭) Fig. 5 Histories of the parameters during the load rejection process (7 s closing) |
甩负荷初始时刻,导叶逐渐关闭,流量稍有上升,转速快速增大,相应的水动力矩和轴向力下降,到2.7 s时转轮所受力矩变为0,稍后轴向力也变为0.导叶继续关闭,水轮机运行于制动工况区,转轮所受水流力矩变为负值,在5.3 s时达到最大,稍后负轴向力也达到最大.7 s后导叶基本关闭,流量基本稳定到8 m3/s,转速下降变缓,转速和轴向力恢复到0附近.
2) 流态分析
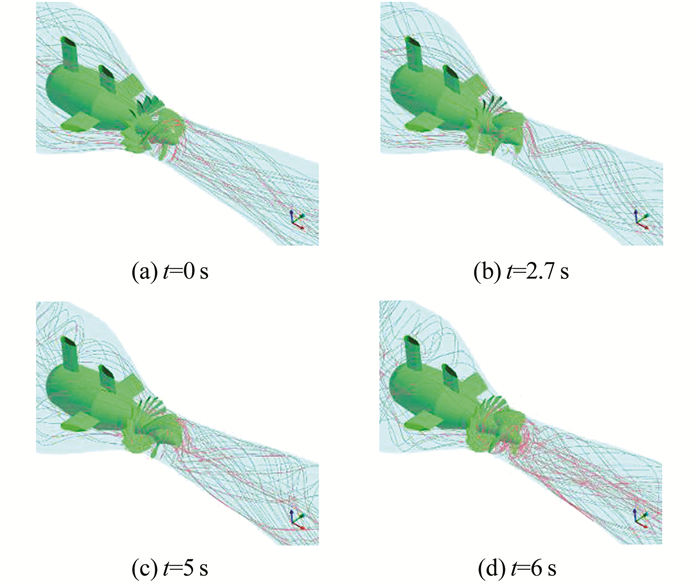
灯泡式水轮机流道为直通流道,截面形状规则,稳定运行时仅在转轮室有强烈的扰动现象.图 6(a)是甩负荷前稳定运行状态,流线直顺稳定.甩负荷后,导叶迅速关闭,由于流量下降,流道内产生水锤波,灯泡体前流线蜷曲,趋近于垂直流道的方向,而灯泡体部分则是以灯泡体为中心的螺旋线(图 6(b)、(c)).
|
| 图 6 甩负荷过程典型流线(7 s导叶关闭) Fig. 6 Typical streamlines during the load rejection process (7 s closing) |
导叶下游从转轮室到尾水管,截面扩大,从转轮出口进入尾水管的水流因受转轮加速旋转而呈现螺旋扩散状流动.甩负荷初期,转轮转速增大,流量减小,转速上升到效率0点时,流线出现了轻微的螺旋现象(图 6(b)).机组运行处于制动工况区时,转轮扰水剧烈,转轮后产生堆积流线并在下游释放,造成了转轮后方尾水管压力变化大,压力脉动明显(图 6(c)~(d)).此外,导叶7 s关闭,关闭速度相对较快,转轮速度变化快,轮毂叶片根部对水流环向加速作用明显低于轮侧缘,尾水管中心流线呈高速射流状.
3) 测点压力脉动时域特性
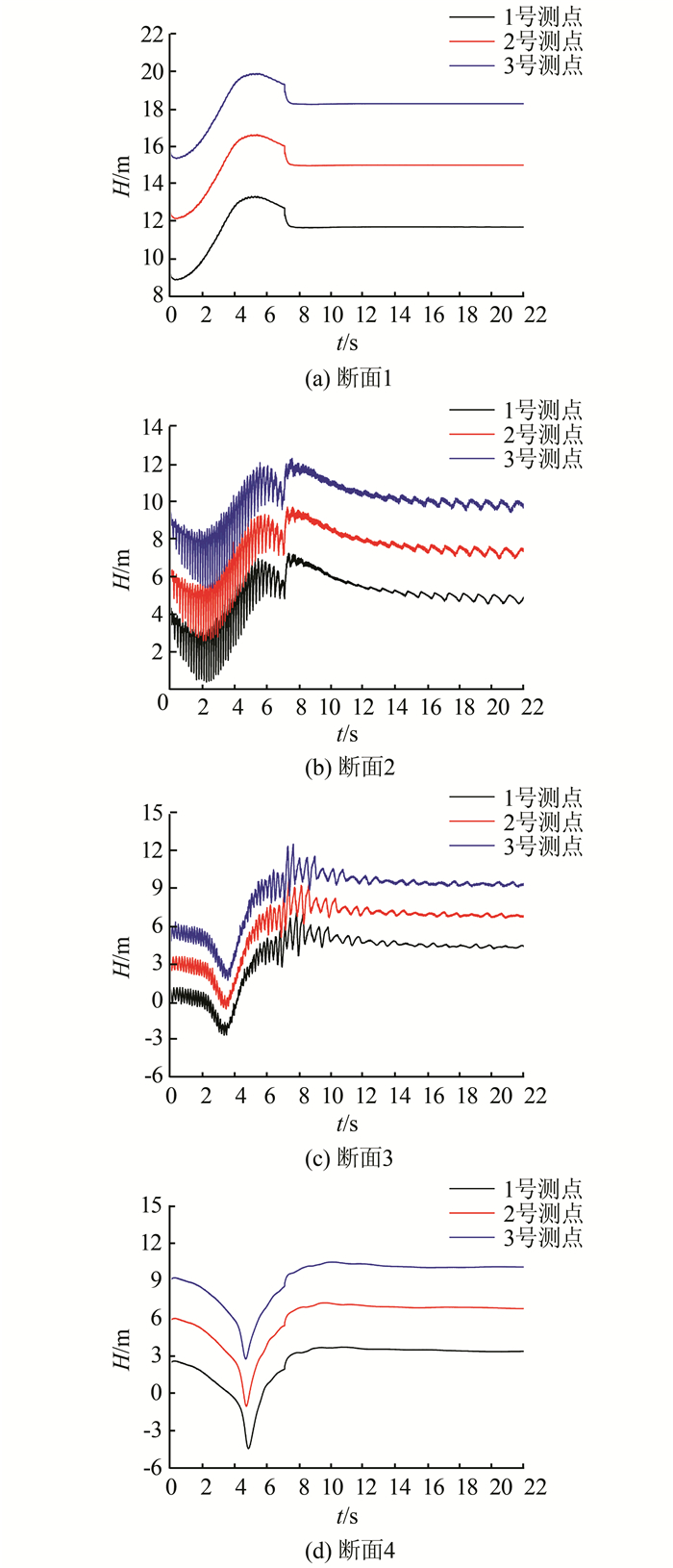
灯泡式机组在甩负荷过程中压力变化剧烈,噪音和振动明显,严重时会对机组安全产生影响.由图 7可见,甩负荷前(t=0 s)各截面上各测点的平均压力近似等于高程对应的静水压强.导叶上游和尾水管处距转轮较远,波动变化小,压力平稳(图 7(a)、(d)).然而在转轮前后,由于动静干涉,转轮前后实时脉动压力较为强烈(图 7(b)、(c))所示,并且由于水流速度加快所产生的低压作用,导致导叶与转轮之间的压力比导叶上游小,转轮出口压力比尾水管出口压力小.
|
| 图 7 不同断面上3个测点压力变化(7 s导叶关闭) Fig. 7 Pressure changes of three monitoring points at different sections (7 s closing) |
甩负荷初期导叶关闭,流量略有增大,导叶损失增大,转轮前压力下降(图 7(a)、(b));转轮后水体受转轮强推扰动,压力瞬时上升,继而也下降(图 7(c)、(d)).
导叶开度继续减小,流量逐渐减小,上游水锤压力增大,断面1测点压力较早回升(图 7(a)).断面2测点压力在转轮转速上升到0效率点附近时达到最小,随后也开始回升(图 7(b)),断面3和4位于转轮后方,受转轮扰动作用显著,负水锤影响时间长,并与尾水涡、动静干涉3者共同作用,压力回升滞后,且尾水管最大负压达-5 m水头.
4) 测点压力脉动频域特性
利用短时傅里叶变换对测点压力进行频谱分析,得出功率密度图,以各断面1号测点为例来了解压力脉动频域特性.
甩负荷过程中,随着转速与流量的升高与降低等一系列不稳定变化,流道内形成复杂的流动结构,其中由于转轮扰动作用,转轮前后脉动变化显著.
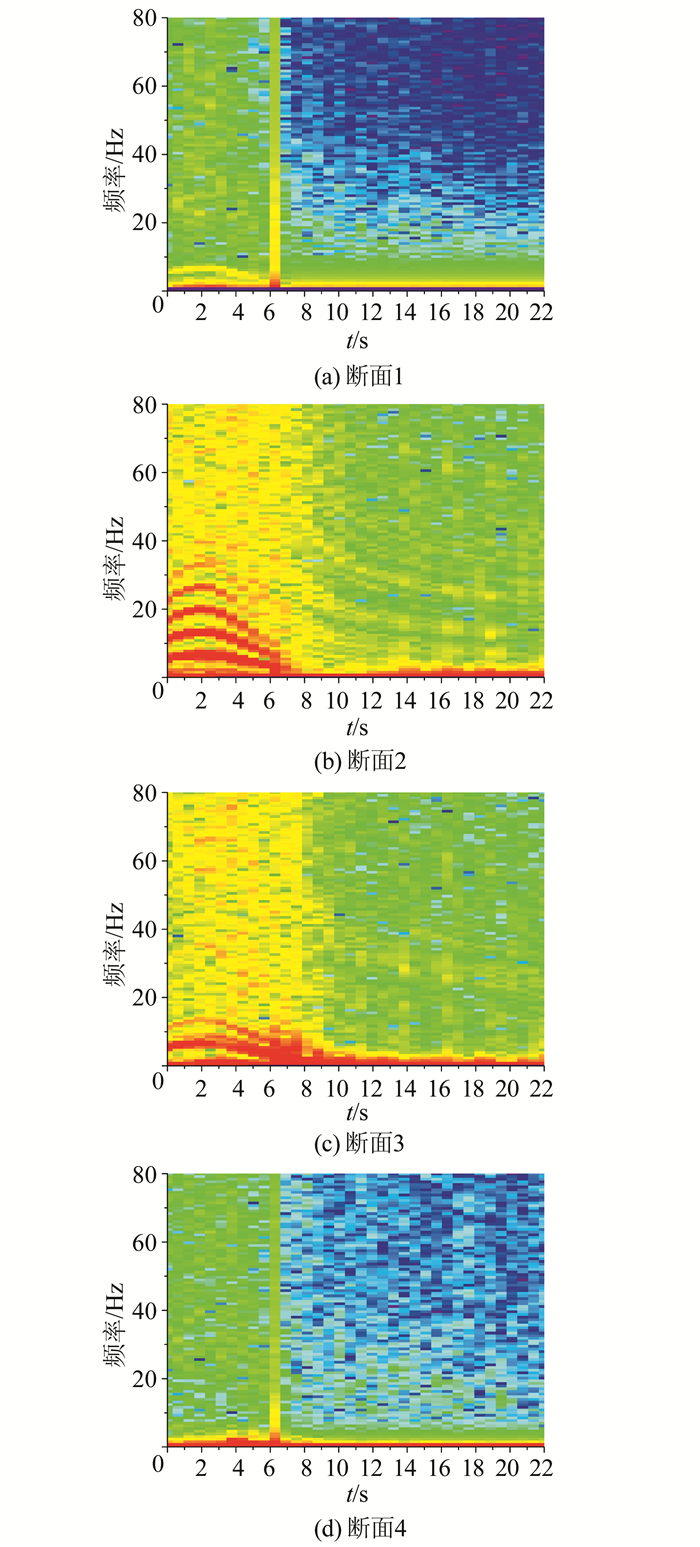
图 8(a)~(d)分别展示了导叶上游侧、导叶与转轮之间、转轮出口以及尾水管处的压力脉动频谱.初始时刻,导叶前频率主要为5 Hz,为3倍转轮频率(稳定工况时转轮转速100 r/min,转轮频率即为1.67 Hz),导叶与转轮之间受到动静干涉影响,频率主要有5、10 Hz和15 Hz 3个高幅值频率,分别为转频的3倍、6倍和9倍,此外还可以明显得出20 Hz和25 Hz等低幅值频率,而转轮后方则主要以5 Hz频率即3倍转频为主.随着甩负荷过渡过程的进行,转轮转速和流量急剧变化,转轮前后脉动频率随时间推进呈先增大后减小的趋势,与转速和流量变化趋势一致(图 8(b)~(c)).导叶上游部位受到导叶的阻隔,尾水管处与转轮相隔较远,脉动频率变化均较微弱,又因导叶关闭速度快,则在导叶关闭结束时刻频率有明显突变(图 8(a)和(d)).
|
| 图 8 各断面1号测点脉动频谱(7 s导叶关闭) Fig. 8 Frequency spectra of pressure fluctuations of point #1 at different sections (7 s closing) |
4) 导叶叶片压力变化
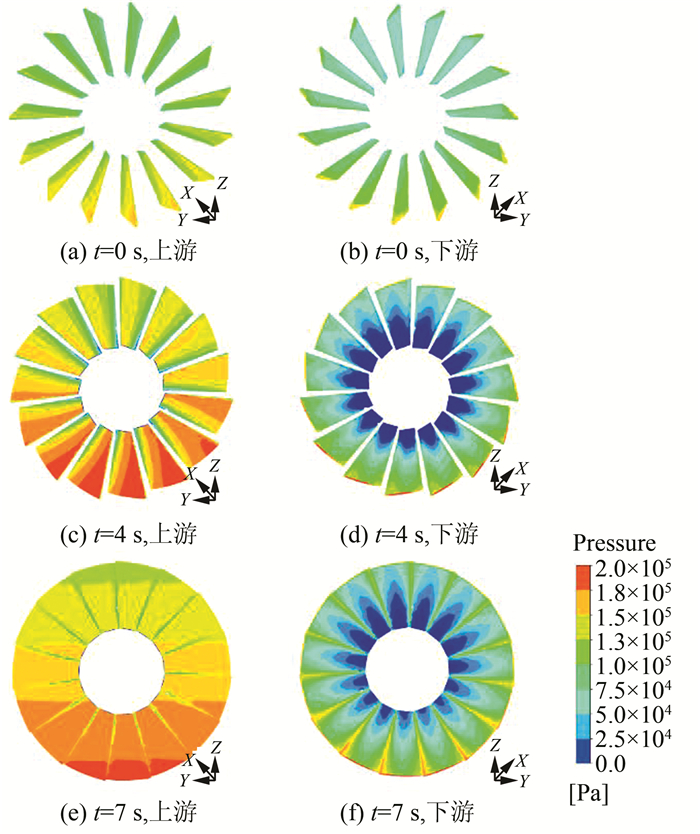
图 9(a)~(c)展示了每个导叶上游表面压力分布,在导叶关闭初始阶段,流量较大,流动分离剧烈,对单个叶片的压力分布影响明显,由于重力作用,压力呈上低下高趋势,并且正向水击波作用使得压力总体增大;导叶逐渐关闭,流速减小,水锤和重力分布叠加,导叶上游侧压力形成水体静压分布规律.导叶下游侧受流动分离和转轮引起的高速旋流影响,导叶根部产生低压区,又因重力作用,上部导叶低压明显(图 9(d)~(f)).
|
| 图 9 导叶压力分布(7 s导叶关闭) Fig. 9 Pressure distribution of the guide vane (7 s closing) |
5) 转轮叶片压力变化
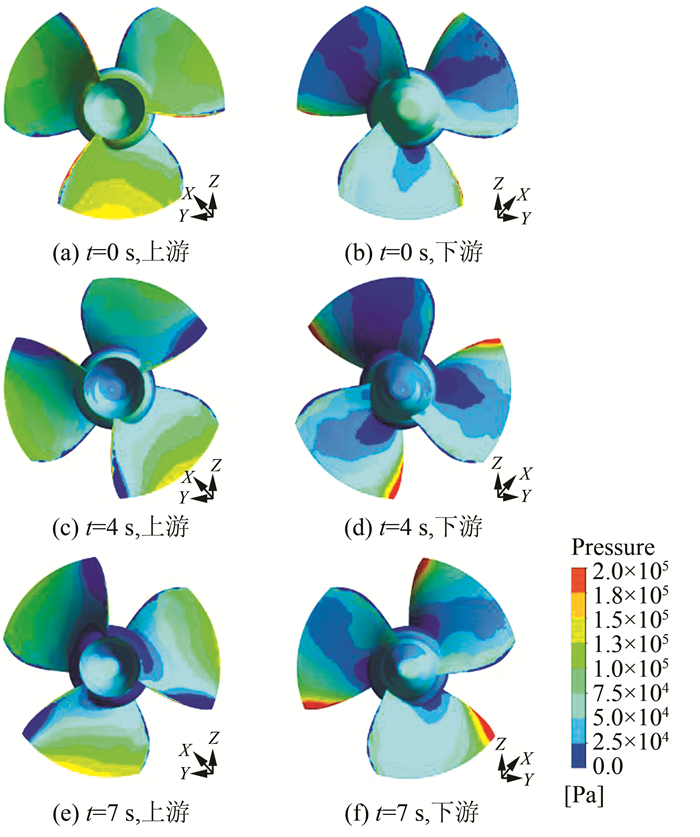
甩负荷过程中,转轮叶片也产生了较为明显的压力变化,如图 10.甩负荷初始阶段,受到水流冲击作用,转轮转速升高,转轮吸力面进水侧叶缘处出现水流剧烈撞击现象,压力升高,压力面的进水侧叶缘处则有严重流动分离现象,压力降低,甚至出现负压,并且在甩负荷过程中水流作用逐渐加大,高压和负压区均增大,叶片表面受力交变明显.
|
| 图 10 转轮压力分布(7 s导叶关闭) Fig. 10 Pressure distribution of the runner (7 s closing) |
1) 压力脉动时域分析
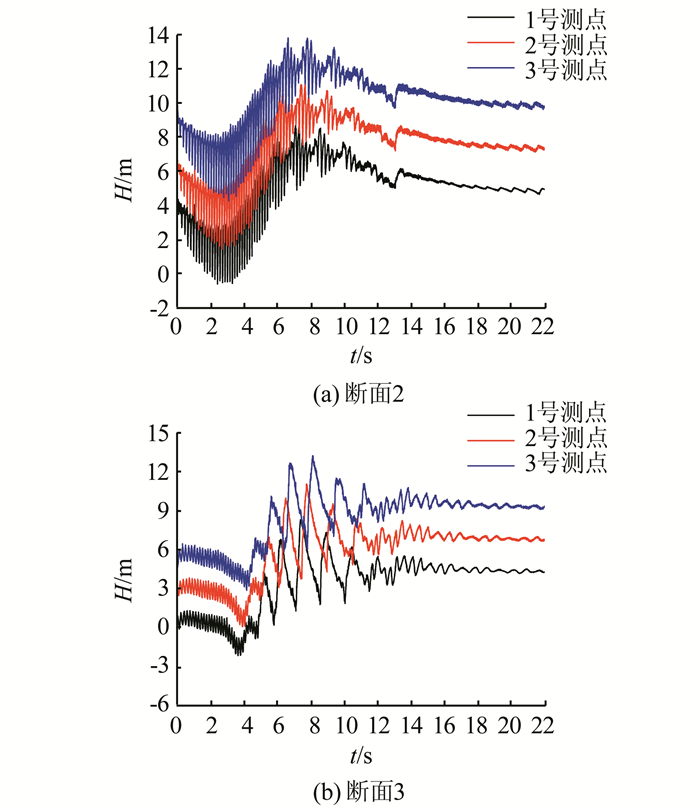
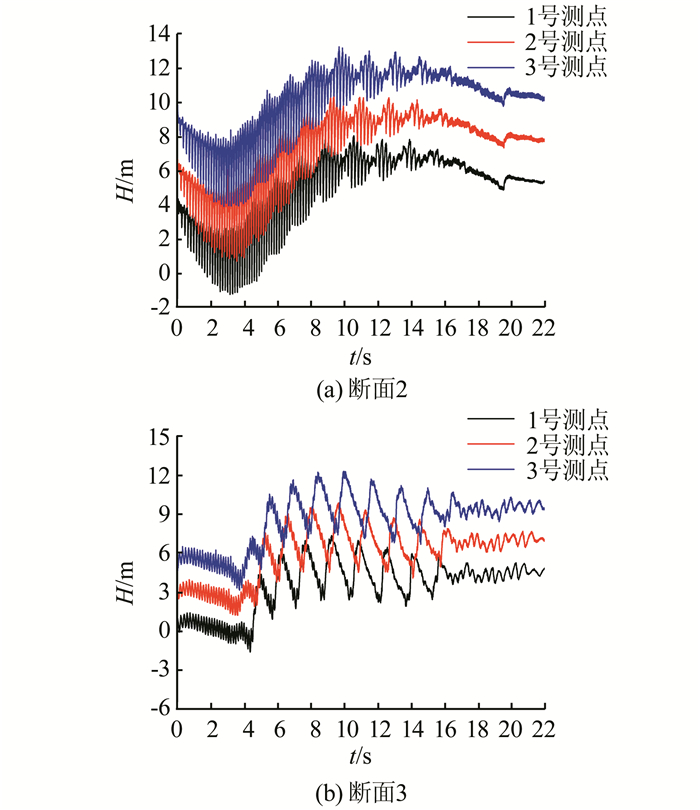
当导叶关闭时间为13 s和20 s时,与7 s关闭的压力变化趋势基本相同,但又有差异,主要体现在断面2和断面3的压力变化.导叶动作缓慢,流场得以发展,导叶上游侧和尾水管内压力变化幅度小.而靠近转轮前后断面受动静干涉影响大,压力脉动幅值高,又因尾水涡带的形成与破灭,转轮出口和尾水管处出现长时间低频脉动波,两处压力脉动呈现明显的大幅度波动现象(图 11(a)~(b)和图 12(a)~(b)),这与文献[11]报道的飞逸现象一致,说明导叶关闭时间延长有可能会带来更大的振动,关闭时间的选择要在满足调保参数要求的同时,协调水锤和尾水管涡带震荡的关系.
|
| 图 11 不同断面上3个测点压力变化图(13 s导叶关闭) Fig. 11 Pressure changes of three monitoring points at different sections (13 s closing) |
|
| 图 12 不同断面上3个测点压力变化图(20 s导叶关闭) Fig. 12 Pressure changes of three monitoring points at different sections (20 s closing) |
2) 压力脉动频域分析
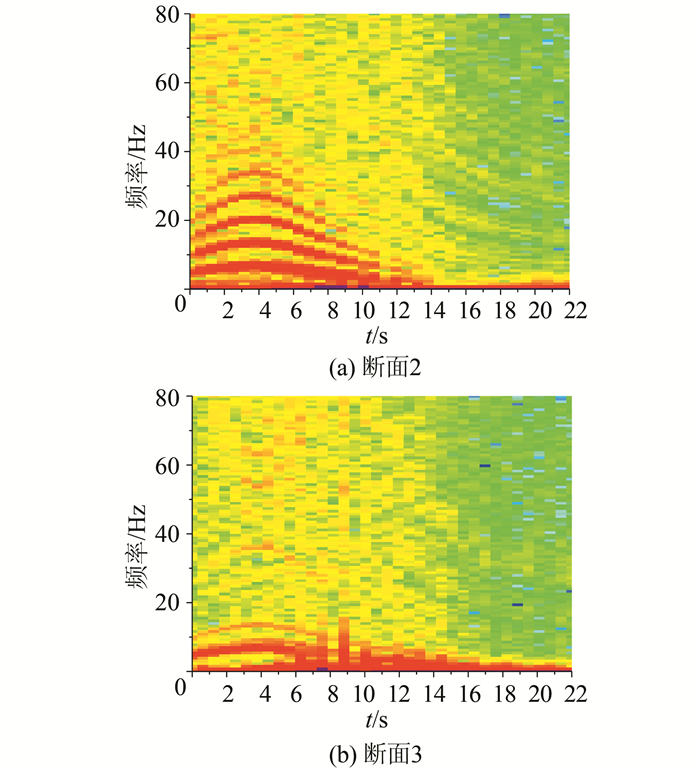
以导叶13 s关闭为例,对各断面1号测点进行短时傅里叶变换,如图 13(a)~(b)所示.分析结果表明,相对于导叶7 s关闭,随着甩负荷过渡过程的进行,水流运动发展充分,脉动变化时间延长,脉动幅值增大,转轮与导叶之间动静干涉加剧(图 13(a)).而在转轮出口和尾水管由于管道扩散作用,则依旧以低频高幅值脉动为主,但幅值较7 s关闭工况增大(图 13(b)),因此常常在尾水管附近有较多较大的震动和噪音.
|
| 图 13 各断面1号测点脉动频谱(13 s导叶关闭) Fig. 13 Frequency spectra of pressure fluctuations of point #1 at different sections (13 s closing) |
3) 涡带分析
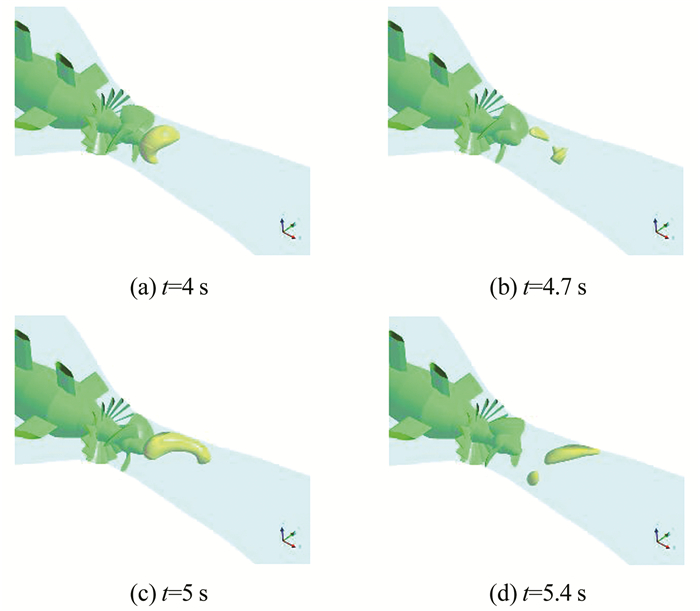
尾水管涡带的产生与破灭对转轮后方和尾水管处的压力波动有较大的影响,以导叶13 s关闭为例,图 14展示了转轮出口处一条涡带从产生到破灭到再生的过程.机组甩负荷过程中,随着转速上升,转轮后压力急剧下降,形成偏心低压涡带,且主要位于流道上半部(图 14(a)),断面3测点1处压力在4 s时降至极小值附近(图 11(c)).因流场发展不充分和重力影响共同作用,涡带在短时间内破灭,发展成断裂涡带(图 14(b)),此时断面3测点1处压力在4.7 s时上升到极大值(图 11(c)),压力脉动产生大波动,并在转轮扰动作用下,继续变大,继而再破灭,压力脉动随之反复波动,说明尾水管压力振荡的根源在于涡的破灭与再生变化.
|
| 图 14 甩负荷尾水管涡带图(13 s导叶关闭) Fig. 14 Vortex band in draft tube during load rejection process (13 s closing) |
本文成功实现了灯泡式水轮机甩负荷过渡过程的三维数值模拟,分析了宏观参数、流态特性及压力脉动特点,并探讨了导叶关闭时间的影响,结论如下:
1) 用动网格实现导叶大角度启闭,用UDF定义转轮转速的方法是可行的.
2) 甩负荷过程中负水锤和正水锤影响明显,导叶前后和叶片正反面压力交变幅值大,并且在重力场作用下,受力分层显著.转轮后方形成剧烈的螺旋高速水流,涡带生成与破灭,造成尾水管强烈振动.
3) 不同的导叶关闭时间对机组运行影响较大,导叶关闭时间越长,转速上升越大,尾水管涡充分发展,导致低频压力脉动强烈,增强了转轮后流动的不稳定性,合理选择关闭时间很重要.
| [1] |
刘延泽, 常近时. 灯泡贯流式水轮机装置甩负荷过渡过程基于内特性解析理论的数值计算方法[J]. 中国农业大学学报, 2008, 13(1): 89-93. Liu Yanze, Chang Jinshi. Numerical method based on internal character for load rejection transient calculation of a bulb turbine installation[J]. Journal of China Agricultural University, 2008, 13(1): 89-93. |
| [2] |
刘延泽, 常近时. 重力场对灯泡贯流式水轮机流场分析及水力性能评估的影响[J]. 水利学报, 2008, 39(1): 96-102. Liu Yanze, Chang Jinshi. Influence of gravity on flow field analysis and hydraulic performance evaluation of bulb turbine[J]. Journal of Hydraulic Engineering, 2008, 39(1): 96-102. DOI:10.3321/j.issn:0559-9350.2008.01.016 |
| [3] |
Gehrer A, Benigni H, Köstenberger M. Unsteady simulation of the flow through a horizontal-shaft bulb turbine[C]//Proceedings of the 22nd IAHR Symposium on Hydraulic Maschines and Systems, Stockholm, 2004.
|
| [4] |
Li J, Yu J, Wu Y.3D unsteady turbulent simulations of transients of the Francis turbine[C]//IOP Conference Series Earth and Environmental Science, 2010: 793-798.
|
| [5] |
Necker J, Aschenbrenner T. Model test and CFD calculation of a cavitating bulb turbine[J]. IOP Conference series: Earth and Environment Science, 2010, 12(1): 012064. |
| [6] |
Yang W, Wu Y L, Liu S H, et al. An optimization method on runner blades in bulb turbine based on CFD analysis[J]. Science China Technological Sciences, 2011, 54(2): 338-344. DOI:10.1007/s11431-010-4261-4 |
| [7] |
Tomaž Kolšek, Jože Duhovnik, Anton Bergant. Simulation of unsteady flow and runner rotation during shut-down of an axial water turbine[J]. Journal of Hydraulic Research, 2006, 44(1): 129-137. DOI:10.1080/00221686.2006.9521668 |
| [8] |
李金伟, 刘树红, 周大庆, 等. 混流式水轮机飞逸暂态过程的三维非定常湍流数值模拟[J]. 水力发电学报, 2009, 28(1): 178-182. Li Jinwei, Liu Shuhong, Zhou Daqing, et al. Three-dimensional unsteady simulation of the runaway transient of the francis turbine[J]. Journal of Hydroelectric Engineering, 2009, 28(1): 178-183. |
| [9] |
周大庆, 吴玉林, 刘树红. 轴流式水轮机模型飞逸过程三维湍流数值模拟[J]. 水利学报, 2010, 42(2): 233-238. Zhou Daqing, Wu Yunlin, Liu Shuhong. Three-dimensional CFD simulation of the runaway transients of a propeller turbine model[J]. Journal of Hydraulic Engineering, 2010, 42(2): 233-238. |
| [10] |
张晓曦, 程永光.灯泡式水轮机三维过渡过程CFD模拟[C]//全国水动力学研讨会并周培源诞辰110周年纪念大会, 2012. Zhang Xiaoxi, Cheng Yongguang. CFD simulation of 3D transients in bulb turbine[C]//National Symposium on Hydrodynamics and the 110th Anniversary of Zhou Peiyuan's Birthday, 2012. |
| [11] |
夏林生, 程永光, 张晓曦, 等. 灯泡式水轮机飞逸过渡过程3维CFD模拟[J]. 四川大学学报(工程科学版), 2014, 46(5): 35-41. Xia Linsheng, Cheng Yongguang, Zhang Xiaoxi, et al. 3D CFD simulation of the runaway transients of bulb turbine[J]. Journal of Sichuan University: Engineering Science Edition, 2014, 46(5): 35-41. |
| [12] |
李师尧, 程永光, 张春泽. IB-LB耦合格式模拟贯流式水轮机三维瞬变流[J]. 华中科技大学学报(自然科学版), 2016(1): 122-127. Li Shiyao, Cheng Yongguang, Zhang Chunze. 3-dimensional transient flow simulation of tubular turbine based on IB-LB[J]. Journal of Huazhong University of Science and Technology (Nature Science Edition), 2016(1): 122-127. |
| [13] |
Li Yiming, Song G, Yan Y. Transient hydrodynamic analysis of the transition process of bulb hydraulic turbine[J]. Advances in Engineering Software, 2015, 90(C): 152-158. |
| [14] |
沙锡林. 贯流式水电站[M]. 北京: 中国水利水电出版社, 1999: 203. Sha Xilin. Tubular Hydropower Station[M]. Beijing: China Water & Power Press, 1999: 203. |
| [15] |
郑源, 张健. 水力机组过渡过程[M]. 北京: 北京大学出版社, 2008: 113. Zhen Yuan, Zhang Jian. Hydraulic Turbine Transition Process[M]. Beijing: Peking University Press, 2008: 113. |
 2018, Vol. 51
2018, Vol. 51




