文章信息
- 徐青, 周祥森, 程志诚
- XU Qing, ZHOU Xiangsen, CHENG Zhicheng
- 基于Ansys的混凝土随机骨料模型及细观力学分析
- Random aggregate model and mesomechanics analysis of concrete based on Ansys
- 武汉大学学报(工学版), 2019, 52(12): 1035-1040, 1047
- Engineering Journal of Wuhan University, 2019, 52(12): 1035-1040, 1047
- http://dx.doi.org/10.14188/j.1671-8844.2019-12-001
-
文章历史
- 收稿日期: 2019-03-22
在混凝土力学特性研究中,细观力学数值分析是一种有效的方法,也是对物理模型试验方法的重要补充.目前,国内外学者在对混凝土细观力学特性的研究过程中,提出的数值仿真模型主要有:随机粒子模型[1]、格构模型[2, 3]、MH模型[4]、统计细观损伤力学模型[5]以及随机骨料模型[6-8]等.
混凝土是典型的多相非均质材料,由水泥浆体、骨料及二者之间的界面过渡区组成.混凝土中骨料形状、大小、含量以及骨料级配等,均影响混凝土的力学特性,同时混凝土还具有尺寸效应.混凝土随机骨料模型是模拟和反映混凝土各组分之间的相互关系、几何形状特征以及在空间或平面的分布特性等混凝土细观力学特性的基础[9, 10].
建立混凝土细观力学模型,真实模拟骨料形状、含量及级配等是关键技术难题.在骨料形状方面,从最简化的圆形骨料,到椭圆形,再到任意多边形;在骨料含量方面,从低含量到高含量;在空间方面,从二维到三维.近年来,骨料投放技术虽然得到了提高,但高含量、任意形状骨料的投放仍然很困难.许多学者提出了不同的骨料投放和控制方法:高政国等[6]研究了混凝土二维凸多边形和三维凸多面体的随机骨料投放算法;孙立国[11]提出了在随机三角形骨料的基础上延伸成多边形的投放方法;马怀发等[12]将圆形骨料内接多边形向外延凸,使其达到圆形骨料模型所占混凝土内截面的面积,有效模拟了骨料的实际形态,维持了骨料的实际级配和含量;严兆等[13]利用块体切割方式生成了随机多边形骨料.在这些算法的基础上,有些学者使用MATLAB、FORTRAN或C语言等编制相应程序实现数值混凝土随机骨料的投放,这种方式可以充分利用不同编程语言的特点和优势,但要实现模型的可视化和有限元程序计算求解,还需编制接口程序,以实现与通用有限元软件(Ansys、Abaqus、Patran/Nastran等)的对接,由此产生了接口程序编制过程复杂、大量参数需在程序之间传递和调用、消耗更多计算内存、整体计算效率低等问题.
为了尽可能避免编制接口程序产生的这些问题,本文利用程序参数化语言APDL,对Ansys有限元平台进行2次开发,探索一种混凝土随机骨料模型生成技术,建立混凝土细观力学模型,并基于损伤力学理论,开展混凝土细观力学损伤研究.该方法实现了从骨料投放、网格划分、模型建立到施加荷载、分析求解等全过程自动化和可视化,操作更便捷,计算过程更高效.
1 混凝土随机骨料生成基本原理 1.1 蒙特卡罗方法在随机骨料模型中,为了模拟骨料在空间或平面的位置、粒径、形状(特指多边形及椭圆骨料的形状)的随机性,应用蒙特卡罗方法主要有两部分工作:①在一定条件下产生均匀分布的随机变量;②利用统计方法确定模型的数字特征,从而得到表征骨料特征的随机参数.应用APDL中的RAND命令,可以省却繁复的数学推导和演算过程,简单快速地生成随机参数.
1.2 Fuller级配曲线骨料粒径分布是混凝土随机骨料模型的重要参数,按照Fuller级配曲线配置混凝土可使混凝土具有最优的密实度和宏观强度.Fuller级配曲线表述为
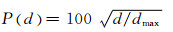 (1)
(1)
式中:P(d)为粒径不超过d的骨料占试件的体积分数;dmax为试件中最大骨料粒径, mm.
1.3 瓦拉文公式三维混凝土细观模型网格数量较二维模型呈指数增加趋势,尤其是椭球形和多边形骨料,建模难度大幅增加,计算量之大使得研究分析过程对计算机硬件要求非常高.瓦拉文对三维随机骨料模型问题进行了简化,基于概率论推导出了二维随机骨料的面积在平面上的分布函数,即瓦拉文公式[14].瓦拉文公式建立了混凝土试件的骨料级配及含量与其内截面所切割骨料面积的关系,使得在二维平面内进行混凝土数值模型细观分析更合理.
假设骨料符合Fuller级配,混凝土试件中任意一点落在骨料区域中的概率为Pk,Pk即是骨料体积占试件体积的百分数,则试件中任意一点落在粒径不超过dx的骨料内的概率为
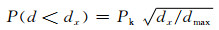 (2)
(2)
对dx求导,得到概率密度公式,即
 (3)
(3)
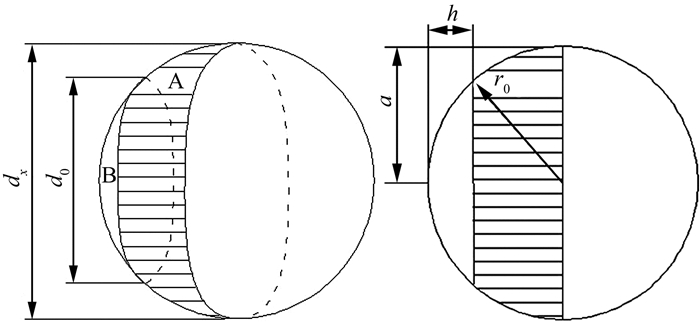
半径小于dx的骨料上的点位于图 1所示球台A上的概率,为球台A的体积VA与半球体积V之比,即Pdx(d>d0)=(V-VB)/V,其中V=πdx3/12,VB=πh(3a2+h2)/6,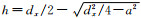
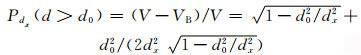 (4)
(4)
|
| 图 1 球形骨料示意图 Fig. 1 Sketch of spherical aggregate |
因此混凝土试件中任意一点位于直径d < d0截面圆内的概率为
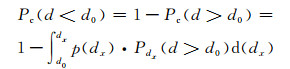 (5)
(5)
将式(5)进行泰勒级数展开,积分得到瓦拉文公式:
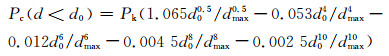 (6)
(6)
瓦拉文公式是建立在球形骨料的基础上,根据骨料的几何关系和概率论推导出来的.对于混凝土的任一截面,从统计意义来讲瓦拉文公式也适用于多边形骨料和椭圆形骨料[12].本研究在二维随机骨料的投放过程中,根据瓦拉文公式确定二维随机骨料模型的骨料含量.
2 生成随机骨料模型的Ansys实现 2.1 骨料级配确定二级配混凝土立方体试件(边长150 mm),最大骨料粒径dmax=40 mm,最小骨料粒径dmin=5 mm,骨料体积分数取Pk=0.628.按式(6)计算,得到骨料级配如表 1所示.表 1中,粒径小于5 mm的骨料未列出,d0为混凝土粒径控制参数,Pc为粒径小于d0的骨料面积与试件截面面积的比值,粒径区间粗骨料面积为骨料粒径范围在相邻两粒径控制参数d0之间的骨料总面积.为简化计算,椭圆骨料粒径取其短轴长,多边形骨料粒径取其外接圆直径.
| d0/mm | d0/ dmax | Pc | 粒径区间粗骨料面积/mm2 | 粗骨料总面积/mm2 |
| 40 | 1.000 | 0.624 | 1 274.260 986.189 2 570.716 1 678.691 1 678.691 |
8 710.843 |
| 30 | 0.750 | 0.567 | ||
| 20 | 0.500 | 0.523 | ||
| 15 | 0.375 | 0.409 | ||
| 10 | 0.250 | 0.334 | ||
| 5 | 0.125 | 0.236 |
确定骨料粒径时,目前大多数方法是:首先选定特定的骨料粒径,计算对应粒径的骨料个数,再由计算机依次投入.鉴于该方法不能保证骨料级配的连续性,本研究随机骨料模型在保证粗骨料总面积不变和骨料级配连续的前提下,为了简化计算,骨料粒径采用蒙特卡罗方法随机产生,然后计算骨料面积,并依次投入骨料,直到达到粗骨料总面积.
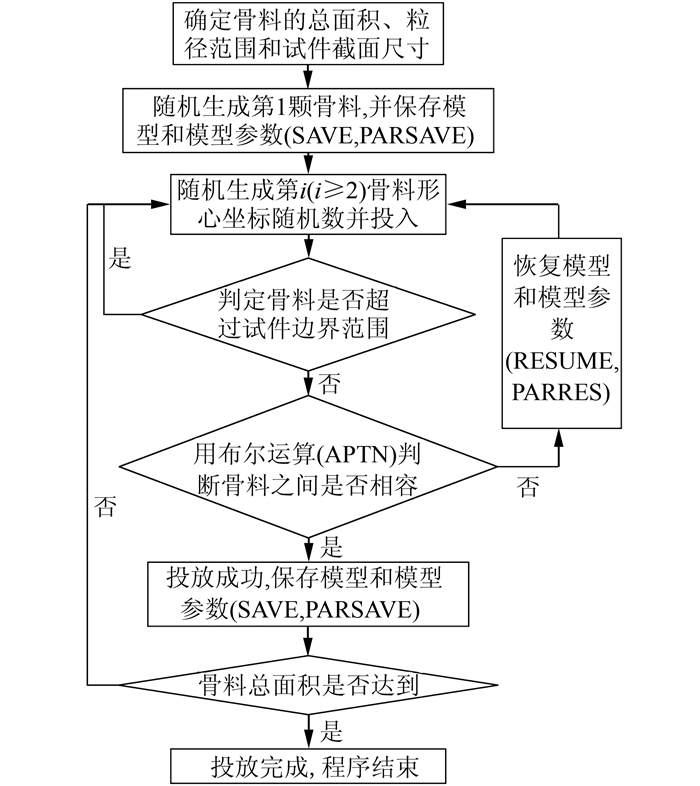
2.2 骨料投放程序控制随机骨料投放流程如图 2所示.在随机骨料模型投放程序中,最关键的是判断新投入骨料与其他骨料之间的相容性.对于圆形骨料,新骨料的圆心与其他骨料圆心之间的距离大于二者的半径之和即可视为骨料之间相容.对于椭圆形骨料和多边形骨料,其外接圆之间相离是骨料之间相容的充分不必要条件.因此,采用外接圆圆心相离作为判断骨料之间是否相容的条件,会浪费较多的投放空间,使投入的骨料含量受限.
|
| 图 2 随机骨料投放流程图 Fig. 2 Flowchart of packing random aggregates |
本文采用Ansys的布尔运算-搭接(Overlap)功能,利用骨料的面积参数可以准确快捷地判断骨料之间是否相容,有效避免了浪费投放空间的问题.新投入一个骨料之后,无需对骨料进行两两搭接运算,仅需3步操作:①使用APTN命令选择所有骨料进行布尔搭接运算;②使用ASUM命令获取布尔运算前后骨料总面积;③判断骨料总面积是否减小,若不减小则相容,若减小则说明新投放的骨料嵌入其他骨料中,此时需要撤销布尔运算并删除投入的新骨料.由于Ansys中无直接的撤销接口,因此需在布尔运算前进行SAVE_DB(保存模型)和PARSAVE(保存模型参数)命令操作,撤销布尔运算并删除投入的新骨料时进行RESUME_DB(恢复模型)和PARRES(恢复模型参数)命令操作.
2.3 骨料生成方法 2.3.1 圆形骨料圆形骨料相对其他骨料较容易生成,投放1个圆形骨料仅需3个随机参数,即圆心坐标(x, y)和直径d.
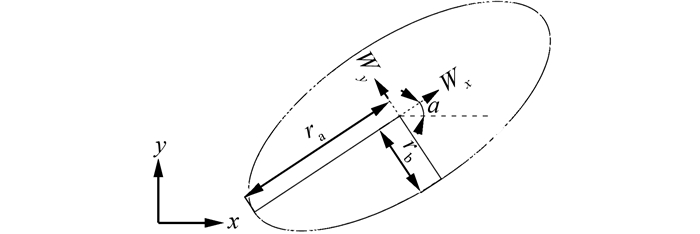
2.3.2 椭圆形骨料由于Ansys中没有直接绘制椭圆的命令和菜单操作,需要激活工作平面(Workplane),工作平面的坐标为(Wx, Wy),如图 3所示.为保证椭圆在试件中位置的随机性,采用WPRO命令将工作平面旋转至随机的角度α(0°≤α≤360°),并将工作平面的笛卡尔坐标系(x, y, z)调整为局部柱坐标系(r, θ, z);另外还需根据椭圆的短长轴比例,用CSWPLA命令修正工作平面中y轴长与x轴长的比例.因此,投放1个椭圆形随机骨料需要5个随机参数,即椭圆中心坐标(x, y)、长半轴ra、短半轴rb,以及旋转角度α.
|
| 图 3 椭圆形骨料示意图 Fig. 3 Sketch of elliptical aggregate |
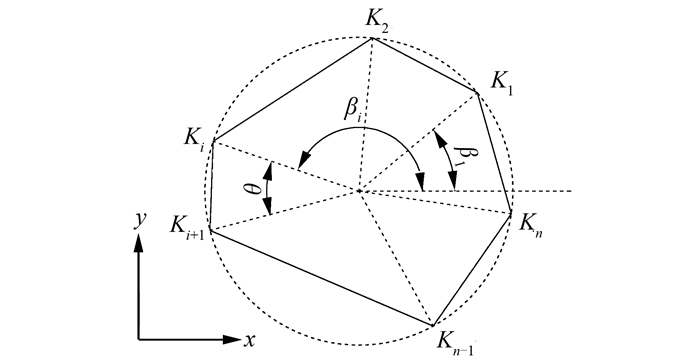
为保证多边形的凸性,首先确定一个直径为d(也认为是多边形骨料的粒径)的圆,根据需要投放多边形的边数,在圆上随机取点确定为关键点,通过关键点生成多边形;然后将圆内关键点集Ki(i=1, 2, …, n)按照βi的大小逆时针排列(βi是关键点Ki和圆心的连线与x轴之间的夹角,见图 4),为避免出现针片状骨料,直线连接随机点与圆心,控制任意相邻关键点与圆心连线之间的夹角θ,使之满足30°≤ θ≤330°;最后逐一连接关键点生成多边形面,如图 4所示.对于多边形骨料,每个骨料需要的随机参数有:多边形外接圆圆心坐标(x, y)、直径d、多边形边数n(3≤n≤8)以及βi(3≤i≤n).
|
| 图 4 多边形骨料示意图 Fig. 4 Sketch of polygonal aggregate |
砂浆与骨料之间界面过渡区(interfacial transition zone, ITZ)厚度Δd通常取0.01~0.1 mm,本研究取Δd=0.1 mm.对于圆形和椭圆形骨料,可通过等比例缩放生成对应的等厚度界面;但对于凸多边形骨料,Ansys没有图形偏移功能,本研究编写了等距偏移算法程序,实现了界面的生成.
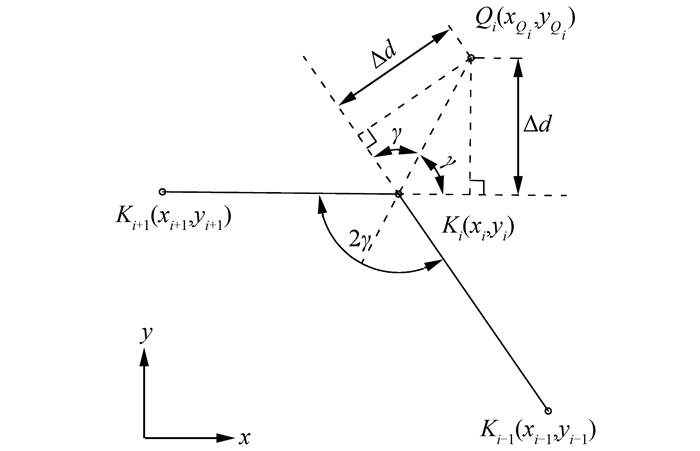
算法如图 5所示,骨料外围边界3个相邻关键点坐标分别为Ki-1(xi-1, yi-1)、Ki(xi, yi)和Ki+1(xi+1, yi+1),Qi为ITZ上对应的关键点,算法的核心是确定ITZ关键点Qi的坐标.Qi到直线Ki-1Ki、Ki+1Ki的距离均为Δd,Qi必定在∠Ki-1KiKi+1的角平分线上.设∠Ki-1KiKi+1=2γ,直线Ki-1Ki、Ki+1Ki的单位向量分别为
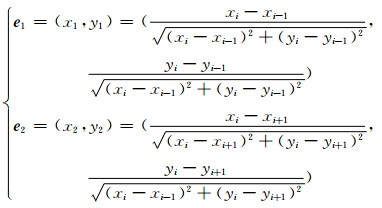 (7)
(7)
|
| 图 5 等距偏移算法生成ITZ示意图 Fig. 5 Sketch of algorithm for creating ITZ |
计算得到:γ=arccos(x1x2+y1y2)/2,则直线KiQi的单位向量表示为
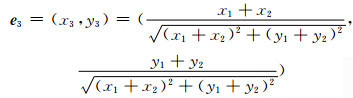 (8)
(8)
进而计算出ITZ所在面关键点Qi的坐标为
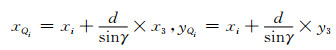 (9)
(9)
确定ITZ各关键点之后,即可在Ansys中通过关键点生成ITZ所在的面.
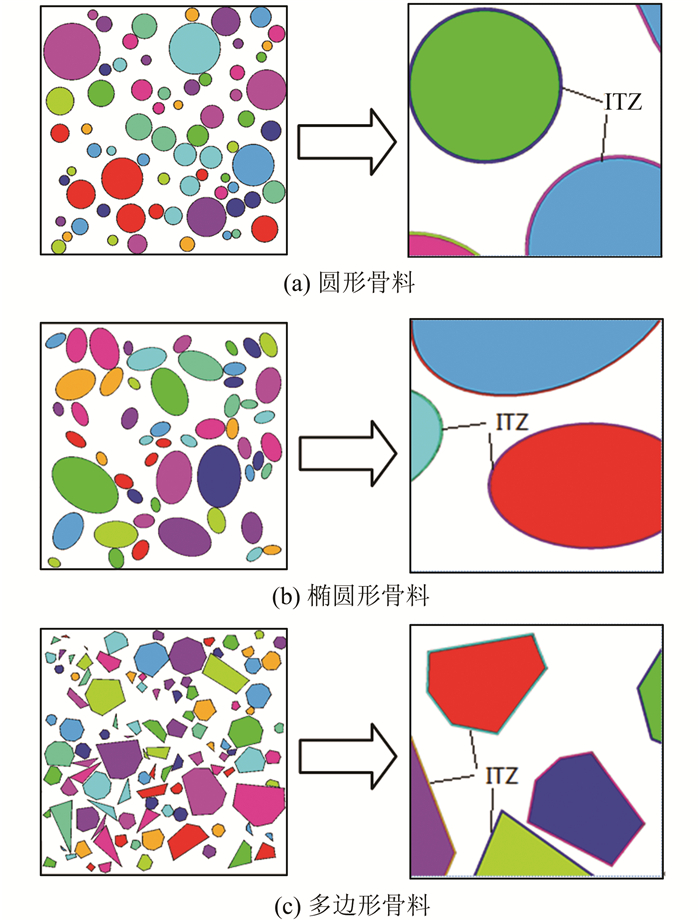
2.5 骨料投放结果骨料含量为62.8%的二维混凝土试件3种骨料形状投放结果如图 6所示.
|
| 图 6 含不同骨料形状的数值混凝土和其局部放大图 Fig. 6 Numerical concretes with different aggregate shapes and their details |
采用本研究提出的随机骨料模型生成技术,基于损伤力学理论,采用准静态位移加载方式,对不同骨料含量混凝土试件开展劈拉数值模拟研究,并验证本研究提出的随机骨料模型生成技术的可行性和有效性.
3.1 网格划分对于二维平面,Ansys提供2种划分网格的方式:自由网格和映射网格.自由网格适用于几何形状较为复杂的模型,而映射网格适用于几何形状规则的模型.2种网格划分方式都可以匹配三角形和四边形单元,三角形单元可看作是退化的四边形单元,其在单元内部的应变是不变的,而四边形单元在内部为双线性变化,使用三角形单元,网格需划分得更密才能保证精度.
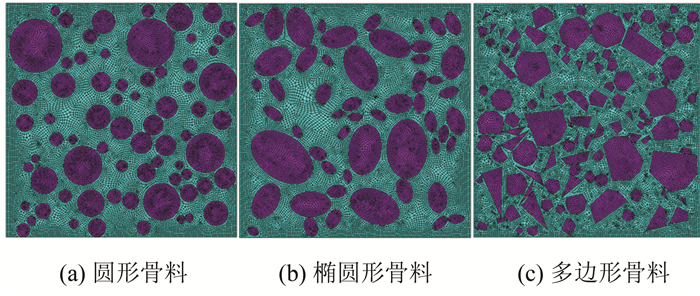
本研究采用自由网格匹配四边形单元对二维平面模型进行网格划分.试件尺寸为150 mm×150 mm,考虑计算机计算效率,控制单元网格尺度为1 mm.如图 7所示.
|
| 图 7 混凝土细观三相有限元网格 Fig. 7 Finite element meshes of numerical concrete |
Mazars[15]损伤模型是基于正交损伤演化法则的一种与割线刚度损失有关的各向同性损伤模型.在加载过程中,混凝土数值试件在线弹性阶段的弹性模量E=E0,损伤阶段弹性模量EM=E0(1-DM),DM为损伤变量.当加载达到初始应变后,损伤变量DM随着试件等效应变增大而增大,直到试件完全破坏,DM=1,EM=0.本文采用Mazars力学损伤模型模拟混凝土试件的劈拉破坏过程.
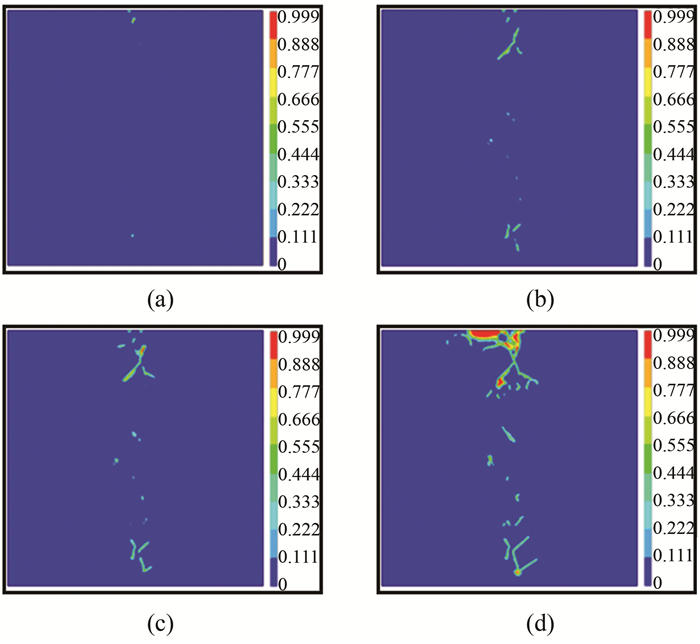
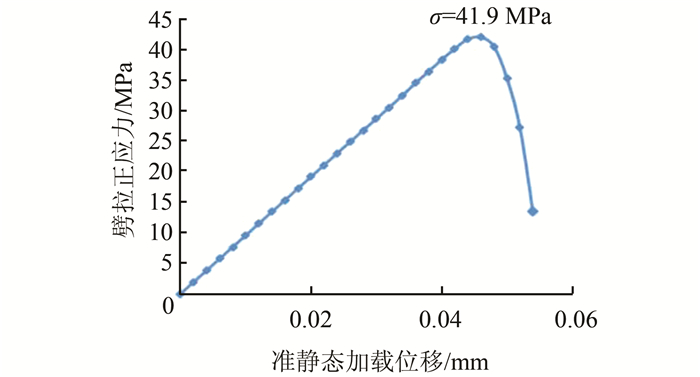
3.3 破坏过程试验采用标准垫条(宽5 mm),在Ansys中对混凝土试件逐级位移加载、求解并输出结果.以含多边形骨料的试件为例,图 8反映了混凝土从逐渐损伤直至完全破坏的过程,可以看出,混凝土基本上沿薄弱界面ITZ发生破坏,符合劈拉破坏机理;图 9为劈拉正应力-准静态加载位移关系曲线,可以看出,劈拉正应力随准静态加载位移先增大后减小,曲线在线性上升过程中,混凝土试件处于弹性阶段,劈拉正应力随着准静态加载位移增大而增大;加载过程中,混凝土试件逐渐出现损伤,试件承受荷载达到峰值后迅速下降,最后完全破坏,整条曲线符合数值试件在弹性阶段和损伤阶段的力学特性.
|
| 图 8 数值混凝土破坏过程 Fig. 8 Failure process of numerical concrete |
|
| 图 9 劈拉正应力-准静态加载位移关系曲线 Fig. 9 Relationship between normal stress and displacement |
图 8、9可以直观地反映数值混凝土劈拉破坏过程,验证了本文随机骨料模型的可行性、准确性、高效性.由图 9可知,峰值正应力为41.9 MPa,根据劈拉强度计算公式:
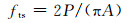
式中:P为施加的力; A为试件劈裂面面积.可以计算出数值多边形骨料混凝土的劈拉强度fts为0.89 MPa.
4 结论1) 在Ansys中的APDL语言可以很好地实现混凝土的随机骨料模型,避免了后处理的求解计算过程中不同软件之间兼容性差、接口程序编制困难的问题.
2) 本文通过Ansys平台上的布尔运算功能,有效便捷地判断了骨料之间的相容性,使得命令流程序更加简洁和精确,还对三维空间随机骨料相容性判断的研究提出了新的思路.
3) 本文通过对Ansys的2次开发,提出了生成多边形骨料等厚度界面ITZ的算法,能较好地模拟混凝土界面ITZ的几何特性.
4) 本文在Ansys平台上,提出了混凝土建模、划分网格、求解分析的全过程研究和全程可视化方法,为细观数值混凝土研究提出了新的视角.
5) 结合损伤力学模型进行的数值混凝土劈拉试验,验证了本文随机骨料模型的可行性和合理性.
| [1] |
Bazant Z P, Tabbara M R. Random particle models for fracture of aggregate or fiber composites[J]. Journal of Engineering Mechanics, 1990, 116(8): 1686-1705. DOI:10.1061/(ASCE)0733-9399(1990)116:8(1686) |
| [2] |
Schlangen E, Garbociz E J. New method for simulating fracture using an elastically uniform random geometry lattice[J]. International Journal of Engineering Science, 1996, 34(10): 1131-1144. DOI:10.1016/0020-7225(96)00019-5 |
| [3] |
Van Mier J G M, Vervuurt A, Van Vliet M R A. Materials engineering of cement-based composites using lattice models[C]// Carpinteri A, Aliabadi M, eds. Computational Fracture Mechanics in Concrete Technology. Sounthampton: WITPress, 1999: 1-32.
|
| [4] |
Mohamed A R, Hansen W. Micro mechanical modeling of concret response under static loading part 1:Model development and validation[J]. ACI Materials Journal, 1999, 96(2): 196-203. |
| [5] |
夏蒙棼, 韩闻生, 柯孚久, 等. 统计细观损伤力学和损伤演化诱致突变(Ⅰ)[J]. 力学进展, 1995, 25(1): 1-23. Xia Mengfen, Han Wensheng, Ke Fujiu, et al. Statistical meso-damage mechanics and damage evolution lead to mutation(Ⅰ)[J]. Advancesin in Mechanics, 1995, 25(1): 1-23. DOI:10.3321/j.issn:1000-0992.1995.01.001 |
| [6] |
高政国, 刘光廷. 二维混凝土随机骨料模型研究[J]. 清华大学学报(自然科学版), 2003, 43(5): 710-714. Gao Zhengguo, Liu Guangting. Two-dimensional random aggregatestructure for concrete[J]. Journal of Tsinghua University (Science & Technology), 2003, 43(5): 710-714. DOI:10.3321/j.issn:1000-0054.2003.05.036 |
| [7] |
Wang Z M, Kwan A K H, Chan H C. Mesoscopic study of concreteⅠ:generation of random aggregate structure and finite element mesh[J]. Computers and Structures, 1999, 70(5): 533-544. DOI:10.1016/S0045-7949(98)00177-1 |
| [8] |
Kwan A K H, Wang Z M, Chan H C. Mesoscopic study of concreteⅡ: nonlinear finite element analysis[J]. Computers and Structures, 1999, 70(5): 545-556. DOI:10.1016/S0045-7949(98)00178-3 |
| [9] |
Huang Y J, Yang Z J, Liu G H, et al. An efficient FE-SBFE coupled method for mesoscale cohesive fracture modeling of concrete[J]. Computational Mechanicals, 2016, 58(4): 635-655. DOI:10.1007/s00466-016-1309-8 |
| [10] |
Ma H F, Chen H Q, Li B K. Influence of meso-structure heterogeneity on dynamic bending strength of concrete[J]. Journal of Hydraulic Engineering, 2005, 36(7): 846-852. |
| [11] |
孙立国.三级配(全级配)混凝土骨料形状数值模拟及其应用[D].南京: 河海大学, 2005. Sun Liguo. Numerical simulation of shape of aggregates of three-graded concrete(full-graded concrete) and application[D]. Nanjing: Hohai University, 2005. |
| [12] |
马怀发, 芈书贞, 陈厚群. 一种混凝土随机凸多边形骨料模型生成方法[J]. 中国水利水电科学研究院学报, 2006, 4(3): 196-201. Ma Huaifa, Mi Shuzhen, Chen Houqun. A generating approach of random convex polygon aggregate model[J]. Journal of China Institute of Water Resources and Hydropower Research, 2006, 4(3): 196-201. DOI:10.3969/j.issn.1672-3031.2006.03.006 |
| [13] |
严兆, 汪卫明. 全级配混凝土随机骨料二维模型生成的块体切割方法[J]. 武汉大学学报(工学版), 2013, 46(4): 484-488. Yan Zhao, Wang Weiming. A method for generating two-dimensional random aggregate model of fully-graded concrete: Block cutting method[J]. Engineering Journal of Wuhan University, 2013, 46(4): 484-488. |
| [14] |
Walraven J C. Aggregate Interlock: A Theoretical and Experimental Analysis[M]. Delft University Press, 1980: 67-72.
|
| [15] |
Mazars J, Pijaudier-Cabot G. Continuum damage theory-application to concrete[J]. Journal of Engineering Mechanic (ASCE), 1989, 115(2): 345-365. DOI:10.1061/(ASCE)0733-9399(1989)115:2(345) |
 2019, Vol. 52
2019, Vol. 52



