文章信息
- 李鹏鹏, 周伟, 熊美林, 杨利福, 徐琨, 来志强
- LI Pengpeng, ZHOU Wei, XIONG Meilin, YANG Lifu, XU Kun, LAI Zhiqiang
- 复杂形状颗粒DEM模拟及其对宏观力学响应影响研究
- Study of DEM modeling of irregular shaped particle and its influence on macromechanical response
- 武汉大学学报(工学版), 2018, 51(6): 478-486
- Engineering Journal of Wuhan University, 2018, 51(6): 478-486
- http://dx.doi.org/10.14188/j.1671-8844.2018-06-002
-
文章历史
- 收稿日期: 2016-06-15
2. 长江勘测规划设计研究院,湖北 武汉 430010
2. Changjiang Institute of Survey, Planning, Design and Research, Wuhan 430010, China
颗粒材料如堆石体、道砟、砂等被广泛应用于大型工程建设中,这些天然材料的工程力学特性不仅受颗粒强度、颗粒间的摩擦系数、级配、孔隙率等物理属性的影响[1],其不规则的颗粒形状也是影响其宏细观力学行为的关键因素之一.目前,通过室内试验研究颗粒形状对颗粒材料力学特性的影响工作量大,且试验条件控制难度大,因此,数值模拟成为研究这一影响的有效方法.
在有限元-离散元耦合分析方法(Combined Finite-Discrete Element Method, FDEM)中,可以采用随机多边形(或多面体)颗粒来模拟颗粒形状[2-6],然而,当颗粒形状拓扑结构比较复杂(如凹多边形)时,FDEM接触检索方法将无法准确识别接触颗粒.在离散元(Discrete Element Method, DEM)模拟中,颗粒的形状多为二维圆盘或三维圆球[7],无法考虑颗粒之间的嵌入咬合作用,数值模拟结果与实际颗粒的力学性质存在一定差异.为此,有学者将形状简单的圆盘或者圆球通过一定的方式组合在一起形成“颗粒簇”或“超级颗粒”(clump单元)来反映颗粒的不规则形状[8-10],clump单元内部的圆盘或圆球可以任意重叠,内部的颗粒之间不产生接触力,整个clump单元作为一个完整的刚性体而存在,其边缘的颗粒与其外部颗粒产生相互作用.此外,在DEM方法中也有以椭圆或者椭球为基本颗粒的,通过改变椭圆的长短轴之比来模拟不同颗粒形状[11-12].上述DEM研究只能模拟一些形状简单且规则的颗粒,对于岩土工程中的复杂形状颗粒往往需要借助图像获取技术才能实现真实颗粒形状的再现.Wang等[13]和金磊等[14]采用CT扫描技术获得颗粒表面信息后,在离散元模拟中用“超级颗粒”重构了真实颗粒形状,但CT扫描方法能提供的颗粒形状很有限,无法反映真实岩土颗粒形状的随机性和多样性.
目前,通过室内试验研究颗粒形状对颗粒集合体宏观力学影响的研究较少;采用抗转动模型[15-16]等效考虑颗粒形状,增加了细观参数且无法充分揭示颗粒形状对细观力学响应的影响.为此,本文提出了复杂形状颗粒DEM模拟方法,首先在有限元软件ANSYS中对生成的随机多边形进行网格划分,随后在PFC2D中用圆盘替换网格,并将多个圆盘交接在一起模拟非规则形状的颗粒(clump单元),实现了包括凹多边形在内的不规则随机多边形颗粒模拟;通过双轴压缩试验,获得了不同形状颗粒试样的宏观力学响应,揭示了颗粒形状对宏观力学响应的细观影响机理.
1 随机多边形生成算法 1.1 多边形颗粒的生成复杂多边形颗粒由边数、极角、圆半径表征确定,如图 1所示.

|
| 图 1 复杂多边形颗粒的表征 Fig. 1 Characterization of polygon particle |
具体生成方法包括如下6个步骤:
步骤1,在指定区域内按照给定级配曲线生成随机圆形颗粒.此时,颗粒圆心位置(x0,y0)和半径r已知.
步骤2,指定最大边数和最小边数,生成多边形随机边数:
 (1)
(1)
式中:n为生成随机多边形的边数;nmin为最小边数;int[]为取整函数;nmax为最大边数;rand为0~1之间的随机数.
步骤3,生成第k条边对应的随机角度
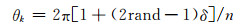 (2)
(2)
式中:θk为第k条边的对角;δ为小于1的常数.上述n个随机角θk之和一般不闭合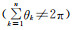
 (3)
(3)
式中: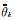
步骤4,获取多边形顶点坐标:
 (4)
(4)
式中:λ为小于1的正常数;grand为服从Gaussian正态分布-1~1之间的随机数;θ′k为修正后的极角;β为颗粒随机方位角;当λ=0时生成的随机多边形为凸多边形,λ≠0时,可以生成凹多边形.
步骤5,根据以上复杂多边形的边数、极角、圆半径等几何信息,在有限元软件ANSYS中生成多边形面,并对各个面进行网格划分.
步骤6,通过在有限元软件ANSYS中获取的网格形心位置及网格面积等信息,在离散元软件PFC2D中用等面积同形心圆盘替换各个网格,并将同一多边形内的圆盘采用clump命令组构成为“超级颗粒”,以此模拟复杂随机多边形.
图 2、图 3分别为λ=0和λ=0.2时生成的随机多边形.当λ=0时,所生成的随机多边形为圆内接凸多边形,随着边数的增加,随机多边形的形状越接近圆.当λ≠0时,本文提出的随机多边形生成方法可以生成凸多边形和凹多边形,当边数较少时,所生成的多边形为凸多边形但与圆无内接关系,随着边数的增加,颗粒形状越来越复杂.

|
| 图 2 生成的凸随机多边形(λ=0) Fig. 2 Polygon particles(λ=0) |

|
| 图 3 生成的复杂随机多边形(λ=0.2) Fig. 3 Polygon particles(λ=0.2) |
图 4为工程中实际岩石颗粒,对比图 2~4,本文提出的复杂形状颗粒模拟方法可以通过参数控制使得生成的颗粒形状更加真实.

|
| 图 4 实际工程中的颗粒 Fig. 4 Particles in actual engineering |
对生成的多边形颗粒进行有限元网格划分,以5边形和10边形颗粒为例,图 5和图 6所示为DEM模拟的颗粒形状.

|
| 图 5 随机5边形DEM模拟结果 Fig. 5 Randomly generated pentagons in the DEM simulations |
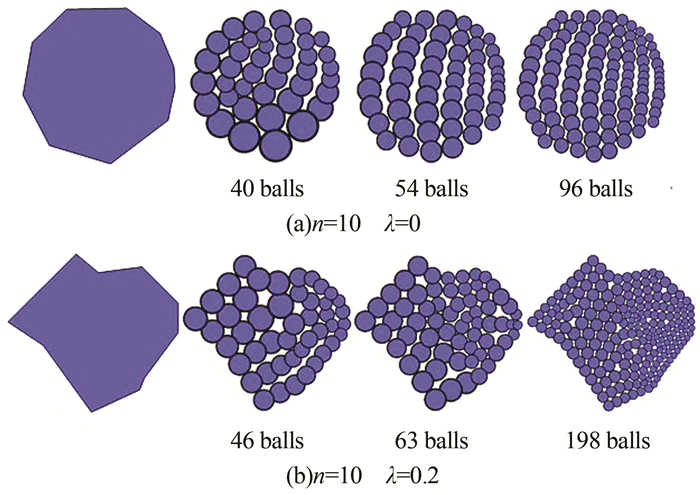
|
| 图 6 随机10边形DEM模拟结果 Fig. 6 Randomly generated decagons in the DEM simulations |
由图 5和6可知,随着小球数目的增加(网格加密),颗粒形状的边界被模拟得越真实.当离散颗粒所采用的网格尺寸越小,所得颗粒边界的凹凸程度(粗糙度)越小但所需的小颗粒数目越大.为了寻找到一个合理计算规模又能控制颗粒粗糙度对宏观力学响应的影响,本文对随机凸多边形采用不同尺寸网格进行离散,网格尺寸以多边形每条边划分的份数为控制指标,最后生成3组不同颗粒粗糙度的同一随机多边形离散元计算模型(颗粒粒径线性分布),计算参数见表 1.
| 法向刚度 kn/(N·m-1) |
切向刚度 ks/(N·m-1) |
摩擦系数f | dmin /m |
dmax /m |
多边形数目 | 围压 /MPa |
| 5×108 | 5×108 | 0.5 | 0.01 | 0.02 | 875 | 1.00 |
根据表 1中参数生成不同颗粒粗糙度的模型,计算结果见图 7.由图可知,颗粒集合体的体积变形与粗糙度关系不明显且差异较小,粗糙度对颗粒集合体的峰值偏应力和残余偏应力的影响较小.因此,可以认为采用划分密度大于每条边3个单元的网格离散后所得到的随机多边形离散元计算结果对颗粒表面粗糙度不敏感.

|
| 图 7 不同小球密度试样计算结果 Fig. 7 Particles in actual engineering numerical simulation results of different density samples |
Barrett[17]提出将颗粒形状量化指标分为颗粒形态、圆度以及表面粗糙度.颗粒表面的粗糙程度通常隐含在颗粒的摩擦系数中,因此只需引入两个颗粒形状指标,即圆度和凹凸度.参考孔亮等[18]对颗粒形状的表征方法,对于二维情况,圆度和凹凸度定义为
 (5)
(5)
式中:S2D和F分别为颗粒的圆度和凹凸度;Af和A′f分别为颗粒面积和颗粒最大内接标准椭圆面积;As为与多边形颗粒等周长圆的面积.为了更便于描述颗粒形状,用颗粒的圆度和凹凸度的加权平均获得表征颗粒外轮廓特征的形状系数,即形状系数K=α1S2D+α2F,其中,α1+α2=1,α1和α2的取值与颗粒的实际形状密切相关,且与颗粒组的受力变形特性也存在联系.在变形过程中,假设颗粒的自转分量比颗粒的平移分量要大,颗粒的圆度影响更大;若平移的分量大,则凹凸度的影响更大[18].本文取形状系数为圆形度和凹凸度的平均值,即K=(S2D+F2D)/2.
颗粒圆度和凹凸度的理论最大值为1.0(纯圆颗粒),图 8为不同规则多边形的形状指标.由图 8可知:随着多边形边数的增加,颗粒的圆度、凹凸度及形状系数K均趋近于1.0.

|
| 图 8 规则形状颗粒形状指标 Fig. 8 Indexes of regular shape particles |
为了分析颗粒圆度对颗粒力学特性的影响,本文建立了6个不同规则多边形形状的颗粒集合体(颗粒边数从5变化到10),通过双轴压缩试验研究颗粒形状对宏观力学响应的影响.试样尺寸为120 mm×60 mm,采用的计算参数见表 1.首先生成了875个圆形颗粒,采用前述方法,取λ=0,控制n的大小,得到表征各个复杂多边形的边数和顶点坐标信息.基于以上信息在有限元软件ANSYS中生成相应的多边形,并对其进行网格控制划分,最后将网格数据导入PFC2D中,用等形心等面积替换法生成不同形状的DEM颗粒.为了使不同形状的颗粒集合体力学响应具有可比性,不同颗粒集合体均在1.0 MPa围压和颗粒摩擦系数μ=0下等向固结,再将摩擦系数设置为0.5后进行加载试验,即保证不同颗粒集合体在加载前均处于最密实状态[19].图 9所示为加载前不同形状颗粒集合体的接触分布图.

|
| 图 9 加载前不同形状颗粒集合体孔隙率及接触分布图 Fig. 9 Porosity and contact distribution of different particle aggregations before loading |
图 9中蓝色线条表示颗粒之间接触数大于1(即边-边接触),红色线条表示颗粒之间只有1个接触关系(即点-点接触或者点-边接触).可以看出,在最密实状态下颗粒间的孔隙填充与颗粒边数(顶点数)有关,当颗粒边数越少时,规则颗粒边-边接触所占的比例越小,其内部的“拱效应”越不明显,形成的“无效颗粒”越少,颗粒填充越密实,孔隙率n越小.
2.2 宏观结果分析为了研究颗粒形状对试样应力变形影响,采用峰值摩擦角φ和剪胀角ψ进行定量描述,按照下式计算:
 (6)
(6)
 (7)
(7)
式中:σ1为大主应力;σ3为施加的围压;εv为体积应变;εa为轴向应变;ε50%为对应于50%峰值偏应力点的轴向应变,对于没有明显峰值的应力应变曲线,峰值偏应力取15%轴向应变对应的偏应力.
图 10为不同试样在双轴压缩下的偏应力及体积变形曲线.从图中可知,不同形状的颗粒集合体在加载初期的变形模量区别不大,体积变形均表现出较小的加载初期剪缩和加载后期剪胀,但强度并不随颗粒边数的增加而单调递减,当规则颗粒边数为5~10时,颗粒集合体的峰值强度和体积变形特性差异较小.

|
| 图 10 不同颗粒形状计算结果 Fig. 10 Numerical simulation results of different particle shapes |
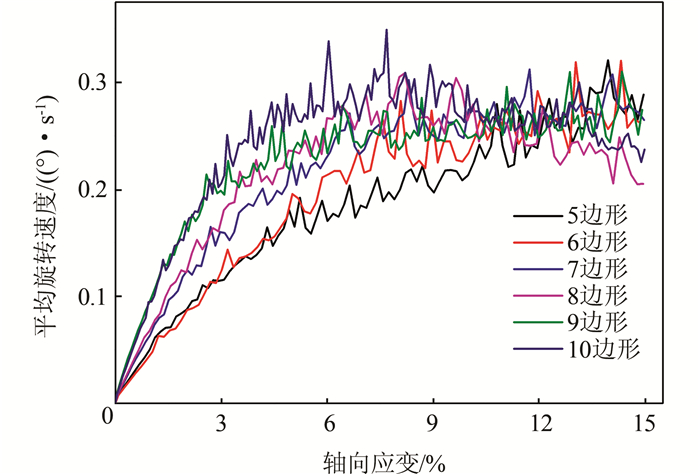
图 11为不同形状试样峰值摩擦角与形状系数K关系曲线,由图可知试样峰值摩擦角与颗粒形状系数存在很好的线性关系.图 12为试样颗粒平均旋转速度演化图,不同形状颗粒的平均旋转速度演化规律与应力应变曲线规律一致,随着颗粒形状边数的增加,平均旋转速度总体上呈增大趋势,但颗粒边数为5~10时,相互区别不大.

|
| 图 11 峰值摩擦角与形状系数关系曲线 Fig. 11 Relationship between peak friction angle and shape factor |
|
| 图 12 颗粒平均旋转速度变化曲线 Fig. 12 Variation of average rotation velocity of particles |
颗粒旋转主要有2种模式:绕形心自转和绕顶点转动,如图 13.不同边数的颗粒外接圆直径相同,在最密实状态下不同形状颗粒绕形心自转同一个角度θ时,颗粒顶点转动的轨迹与外接圆重合,颗粒边数越少,颗粒每一个顶点与圆心连线转过的面积总和与颗粒面积之差越大.当颗粒转动一个圆心角时,颗粒顶点与圆心连线转过的面积之和为外接圆的面积,颗粒边数越多,颗粒面积越接近其外接圆面积,即颗粒边数越多,颗粒转动所需的额外空间越少.以5边形和6边形为例,5边形颗粒转动一个圆心角时,试样体积增大10A1,6边形试样体积增大12A2,显然有10A1>12A2,因此颗粒绕形心自转时,颗粒边数越少局部剪胀越大,当颗粒边数相差越大时,剪胀变形差异越大.由于点-点或点-边接触比较不稳定,因此这种接触容易绕颗粒接触点转动,且在加载过程中,颗粒顶点数越多,发生点-点或点-边接触的概率越大.当颗粒绕顶点转动时,偶数边颗粒的旋转半径R2等于其外接圆的直径,奇数边颗粒旋转半径R1 < R2,因此偶数边颗粒绕顶点转动时,试样剪胀变形更大.

|
| 图 13 颗粒旋转模式 Fig. 13 Particle rotation modes |
图 14为加载过程中不同试样边-边接触比例关系演化图,从图可知在最密实状态下颗粒接触以边-边接触为主,随着加载进行,边-边接触比例逐渐降低.图 10中的峰值强度和体积变形并没有出现与颗粒形状单调变化的关系,这可以用颗粒旋转加以解释:加载过程中颗粒绕自身旋转,导致试样局部体积剪胀,颗粒边数越少剪胀越严重,颗粒“摆脱”周围约束所需能量越大,因此试样峰值强度越大;当颗粒边数相差很小时,颗粒顶点数的增加使得点-点和点-边接触的概率增加,颗粒发生绕顶点旋转的可能性增大,因此偶数边颗粒与奇数边颗粒的体积变形差异较小.同时,与绕形心旋转相比,颗粒绕顶点旋转时,颗粒转动惯量增大,所需外力矩增大,因此偶数边颗粒试样的峰值强度未明显降低.

|
| 图 14 试样边-边接触比例关系演化图 Fig. 14 Variations of proportion of face-to-face contact |
下式是由Oda[20]提出的定量描述颗粒接触法向的组构张量,组构张量主值φ11和φ22能够很好地表征颗粒接触形成和失效程度,在二维情况下有φ11+φ22=1.该式为
 (8)
(8)
式中:n为接触面法向的单位矢量;Θ描述了全局坐标系中单位矢量n法向;E(Θ)是接触法向的概率密度函数.
图 15为加载结束时颗粒接触分布图,由图可知,颗粒边数越少,拱效应越明显,拱内的空隙越大.图 16为试样组构张量主值φ11演化图(下角标1表示为围压方向,下角标2表示为加载方向),由图可知在加载过程中,由于颗粒滑动和颗粒转动(即颗粒位置调整),加载方向上不断有新接触形成而围压方向上的接触不断失效,且颗粒边数越少,试样中颗粒接触失效与重构越激烈.图 15和图 16的结果印证了上述对图 10的解释,即颗粒边数越少颗粒位置调整越强烈,其形成的力链稳定结构(拱结构力链)越多,试样整体强度最高且剪胀最明显.

|
| 图 15 加载结束时不同形状颗粒集合体接触分布图 Fig. 15 Contact distribution of different particle aggregations after loading |

|
| 图 16 接触法向组构张量演化图 Fig. 16 Evolutions of fabric tensor on contact normal |
在上节875个圆形颗粒中,随机生成5~10边的随机多边形,分别取λ=0,0.1,0.2,0.3生成4组不同凹凸度的试样,并在1.0MPa围压和颗粒摩擦系数μ=0下等向固结,再将摩擦系数设置为0.5后进行加载试验.
图 17为不同试样在双轴压缩下的偏应力及体积变形曲线.从图中可知,当试样颗粒全部为凸颗粒(λ=0)时,试样的峰值强度最低,且变形模量也最小.当λ≠0时,试样的变形模量比λ=0时大,但不同λ的试样初始变形模量差异很小;随着λ值的增大,试样的峰值强度先增大后减小,说明随着颗粒凹凸度变化幅度的增加,试样在最密实状态下的咬合作用明显增强,但这种咬合作用在λ=0.2时最强.当λ从0增大到0.2时,试样的剪胀变形增大,而后开始变小,这与峰值偏应力结果一致.说明在最密实状态下,当颗粒形状更加随机多样时,颗粒间的排列更加密实,咬合作用更强,颗粒的旋转需要更多的外部能量和旋转空间;同时,颗粒形状随机多样性与颗粒间的咬合作用并无单调关系,当λ=0.2时咬合作用最强,峰值强度最高,变形模量最大.

|
| 图 17 不同颗粒形状计算结果 Fig. 17 Numerical simulation results of different particle shapes |
本文提出了复杂形状颗粒DEM模拟方法,通过双轴压缩试验研究了颗粒形状对强度变形的影响,并从细观层次上解释其影响机制,主要结论如下:
1) 提出了复杂形状颗粒DEM模拟方法,在PFC2D中实现了包括凹多边形在内的复杂形状颗粒模拟,通过参数控制使得生成的颗粒形状更加真实.
2) 在最密实状态下,颗粒间的孔隙填充与颗粒边数有关,颗粒边数越少,孔隙率越小.这主要是由于颗粒的边数越少,周长越短,力链中的稳定接触(边-边接触)所占比例越少,试样内部的拱效应越不明显,形成的“无效颗粒”越少,颗粒填充越密实.
3) 在最密实状态下,不同形状颗粒集合体加载初期的变形模量很接近,偏应力和体积变形规律相似,峰值摩擦角与形状系数K呈线性关系,但规则颗粒边数为5~10时,颗粒集合体的峰值强度和体积变形特性差异较小.
4) 在双轴压缩过程中,颗粒边数越少的试样,颗粒位置调整(颗粒滑动和颗粒转动)越剧烈.颗粒形状对颗粒集合体宏观力学响应的影响可以从细观层次上解释为:颗粒边数越少,颗粒绕形心转动所需外界功越大,所导致的体积剪胀也越明显;颗粒绕接触点旋转时,偶数边颗粒所需外界功和导致的体积剪胀比奇数边颗粒试样大,因此随着颗粒边数的降低,试样峰值强度和剪胀变形越大.边数为5~10的试样宏观响应差异很小这一现象可通过相应的边-边接触比例关系演化结果以及接触法相组构张量演化结果得到解释.
5) 在最密实状态下,当试样颗粒全部为凸颗粒时,试样的峰值强度和变形模量最小.随着颗粒凹凸度变化幅度的增加,颗粒间的排列更加密实,咬合作用更强,颗粒的旋转需要更多的外部能量和旋转空间,但颗粒形状随机多样性与颗粒间的咬合作用并无单调关系,当λ=0.2时咬合作用最强.
6) 本文所提出的这一复杂形状颗粒模拟方法中,为使颗粒形状的边界被模拟得更真实,离散颗粒所采用的网格需划分得更细,即颗粒数目更大,计算工作量会更大.但是以目前的计算机硬件水平,在二维条件下的计算速度是可以接受的.如何优化此方法,减少颗粒数目,将是下一步的研究工作.
| [1] |
周健, 池毓蔚, 池永, 等. 砂土双轴试验的颗粒流模拟[J]. 岩土工程学报, 2000, 22(6): 701-704. Zhou Jian, Chi Yuwei, Chi Yong, et al. Simulation of biaxial test on sand by particle flow code[J]. Chinese Journal of Geotechnical Engineering, 2000, 22(6): 701-704. DOI:10.3321/j.issn:1000-4548.2000.06.014 |
| [2] |
周伟, 常晓林, 周创兵, 等. 堆石体应力变形细观模拟的随机散粒体不连续变形模型及其应用[J]. 岩石力学与工程学报, 2009, 28(3): 491-499. Zhou Wei, Chang Xiaolin, Zhou Chuangbing, et al. Stochastic granule discontinuous deformation model of rockfill and its application[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(3): 491-499. DOI:10.3321/j.issn:1000-6915.2009.03.007 |
| [3] |
马刚, 周伟, 常晓林, 等. 锚杆加固散粒体的作用机制研究[J]. 岩石力学与工程学报, 2010, 29(8): 1577-1584. Ma Gang, Zhou Wei, Chang Xiaolin, et al. Study of anchorage mechanism of granular mixture[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(8): 1577-1584. |
| [4] |
严成增, 郑宏, 孙冠华, 等. 粗粒料多边形表征及二维FEM/DEM分析[J]. 岩土力学, 2015(S2): 95-103. Yan Chengzeng, Zheng Hong, Sun Guanhua, et al. Polygon characterization of coarse aggregate and two-dimensional combined finite discrete element method analysis[J]. Rock and Soil Mechanics, 2015(S2): 95-103. |
| [5] |
Zhao G J. Fourier-Voronoi-based generation of realistic samples for discrete modelling of granular materials[J]. Granular Matter, 2012, 14(5): 621-638. DOI:10.1007/s10035-012-0356-x |
| [6] |
刘洋, 李晓柱, 吴顺川. 多块体形状堆石体碾压颗粒破碎数值模拟[J]. 岩土力学, 2014, 35(11): 3269-3280. Liu Yang, Li Xiaozhu, Wu Shunchuan. Numerical simulation of particle crushing for rockfill of different particles shape under rolling compaction[J]. Rock and Soil Mechanics, 2014, 35(11): 3269-3280. |
| [7] |
Cundall P A. Formulation of a three-dimensiona distinct element model-part Ⅰ: A scheme to detect and represent contacts in system composed of many polyhedral blocks[J]. Int. J Rock Mech., Min. Sci. & Geomech.Abstr, 1988, 25(3): 107-116. |
| [8] |
Jensen R P, Bosscher P J, Plesha M E, et al. DEM simulation of granular media—structure interface: effects of surface roughness and particle shape[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1999, 23(6): 531-547. DOI:10.1002/(ISSN)1096-9853 |
| [9] |
Ferellec J F, McDowell G R. A simple method to create complex particle shapes for DEM[J]. Geomechanics and Geoengineering: An International Journal, 2008, 3(3): 211-216. DOI:10.1080/17486020802253992 |
| [10] |
Mollanouri Shamsi M M, Mirghasemi A A. Numerical simulation of 3D semi-real-shaped granular particle assembly[J]. Powder Technology, 2012, 221: 431-446. DOI:10.1016/j.powtec.2012.01.042 |
| [11] |
李立青, 蒋明镜, 吴晓峰. 椭圆形颗粒堆积体模拟颗粒材料力学性能的离散元数值方法[J]. 岩土力学, 2011(S1): 713-718. Li Liqing, Jiang Mingjing, Wu Xiaofeng. A developed discrete element model NS2D for simulating mechanical properties of elliptical particles assemblages[J]. Rock and Soil Mechanics, 2011(S1): 713-718. |
| [12] |
蒋明镜, 李立青, 申志福. 双剪类流动模型的非圆形颗粒离散元数值验证[J]. 岩土工程学报, 2013(4): 619-626. Jiang Mingjing, Li Liqing, Shen Zhifu. Evaluation of double-shearing type kinematic models for granular flows by use of distinct element methods for non-circular particles[J]. Chinese Journal of Geotechnical Engineering, 2013(4): 619-626. |
| [13] |
Wang L, Park J Y, Fu Y. Representation of real particles for DEM simulation using X-ray tomography[J]. Construction and Building Materials, 2007, 21(2): 338-346. DOI:10.1016/j.conbuildmat.2005.08.013 |
| [14] |
金磊, 曾亚武, 李欢, 等. 基于不规则颗粒离散元的土石混合体大三轴数值模拟[J]. 岩土工程学报, 2015(5): 829-838. Jin Lei, Zeng Yawu, Li Huan, et al. Numerical simulation of large-scale triaxial tests on soil-rock mixture based on DEM of irregularly shaped particles[J]. Chinese Journal of Geotechnical Engineering, 2015(5): 829-838. |
| [15] |
蒋明镜, 李秀梅, 胡海军. 含抗转能力散粒体的宏微观力学特性数值分析[J]. 计算力学学报, 2011, 28(4): 622-628. Jiang Mingjing, Li Xiumei, Hu Haijun. Numerical investigation on macro-micro mechanical behaviours of granular materials incorporating rolling resistance[J]. Chinese Journal of Computational Mechanics, 2011, 28(4): 622-628. |
| [16] |
蒋明镜, 王富周, 朱合华. 单粒组密砂剪切带的直剪试验离散元数值分析[J]. 岩土力学, 2010, 31(1): 253-257. Jiang Mingjing, Wang Fuzhou, Zhu Hehua. Shear band formation in ideal dense sand in direct shear test by discrete element analysis[J]. Rock and Soil Mechanics, 2010, 31(1): 253-257. DOI:10.3969/j.issn.1000-7598.2010.01.043 |
| [17] |
Barrett P J. The shape of rock particles, a critical review[J]. Sedimentology, 1980, 27(3): 291-303. DOI:10.1111/sed.1980.27.issue-3 |
| [18] |
孔亮, 彭仁. 颗粒形状对类砂土力学性质影响的颗粒流模拟[J]. 岩石力学与工程学报, 2011, 30(10): 2112-2119. Kong Liang, Peng Ren. Partical flow simulation of influence of particle shape on mechanical properties of quasi-sands[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(10): 2112-2119. |
| [19] |
黄青富, 詹美礼, 盛金昌, 等. 基于颗粒离散单元法的获取任意相对密实度下级配颗粒堆积体的数值方法[J]. 岩土工程学报, 2015(3): 537-543. Huang Qingfu, Zhan Meili, Sheng Jinchang, et al. Numerical method to generate granular assembly with any desired relative density based on DEM[J]. Chinese Journal of Geotechnical Engineering, 2015(3): 537-543. |
| [20] |
Oda M, Konishi J, Nemat-Nasser S. Experimental micromechanical evaluation of strength of granular materials: effects of particle rolling[J]. Mech. of Mater, 1982, 1(4): 269-283. DOI:10.1016/0167-6636(82)90027-8 |
 2018, Vol. 51
2018, Vol. 51




