文章信息
- 卢海林, 蔡恒, 黄民水, 杨宏印
- LU Hailin, CAI Heng, HUANG Minshui, YANG Hongyin
- 薄壁曲线箱梁剪滞翘曲位移模式研究
- A Shear lag warping displacement mode research of thin-walled curved box girder
- 武汉大学学报(工学版), 2019, 52(1): 40-45, 94
- Engineering Journal of Wuhan University, 2019, 52(1): 40-45, 94
- http://dx.doi.org/10.14188/j.1671-8844.2019-01-007
-
文章历史
- 收稿日期: 2017-09-12
2. 武汉大学土木建筑工程学院,湖北 武汉 430072
2. School of Civil and Architectural Engineering, Wuhan University, Wuhan 430072, China
在桥梁设计中,宽翼缘的薄壁箱形梁是一种常见的结构形式,它除了具有抗扭刚度大之外,还具有自重轻、挖空率高、材料用料少、适应于布置管线等优点,因而被广泛用于城市立交和高架桥建设中.剪力滞效应[1]是指箱梁在竖向弯曲时,由翼板剪切变形非均匀分布而引起的弯曲法向正应力沿板宽方向分布不均匀的现象.研究表明剪力滞不仅会产生应力集中现象,造成梁体局部开裂[2],还会削弱弯梁的刚度,引起附加挠度的增大[3],影响结构的安全性和耐久性.国内外学者对此展开了大量的研究,提出了许多方法,主要包括比拟杆法、能量变分法、有限元数值解法、工程试验等,其中,基于最小势能原理的能量变分法不仅能获得闭合解[4, 5],而且求解的肋板交界处的应力峰值与实际比较接近,因而被广泛地采用.薄壁箱梁在静载作用下的剪力滞理论日益得到完善.
桥梁除了承受自重外,还主要承受车辆动荷载、温度效应,有时还会遭遇风灾和地震作用,基于此,学者们对动荷载作用下薄壁箱梁剪力滞效应进行了相应的研究.冀伟等[6]对波形钢腹板PC连续箱梁桥自振频率进行了理论分析与试验研究;甘亚南等[7, 8]基于能量变分原理对矩形薄壁箱梁自振特性进行了分析,并考虑了多参数翘曲位移函数的影响;周旺保等[9]推导了薄壁箱梁的自振频率计算公式,考虑了应力自平衡的剪力滞和剪切变形等影响.上述研究均是针对直线箱梁,受车辆动荷载的冲击和竖向地震的激励,曲线箱梁不仅会产生强烈的弯、扭、剪力滞耦合变形,截面还会发生畸变、翘曲,而自振频率又是反映结构动力特性的一个重要参数,使其在动荷载作用下的内力和变形计算趋于复杂化,特别是使用《桥规》[10]计算冲击系数时尤为如此.
假定翼板的剪力滞翘曲位移模式是应用能量变分法的基础和前提,它直接关系到求解的精度.本文在查阅已有的相关文献基础上,分别假定剪力滞翘曲位移按抛物线系列[11-13]、余弦函数[14]、指数函数、悬链线[8]分布,基于最小势能原理,综合运用能量变分法和Hamilton原理导出曲线箱梁振动控制微分方程,并获得竖向弯曲自振基频显示解,同时寻找精度较高的剪力滞翘曲位移模式,为同类研究提供参考.
1 振动控制微分方程 1.1 基本假定与剪翘位移模式为简化力学模型,现做如下基本假定:
1) 材料处于线弹性阶段;
2) 不计入阻尼的影响;
3) 上下翼缘板的变形不符合平截面假定,而腹板的变形符合平截面假空,不计入畸变影响;
4) 纵向线应变考虑初曲率的影响,只在竖向弯曲中计入剪力滞效应;
5) 忽略平面外的横向应变和剪应变,即εy=εz= 0,γyz=γxz=0,竖向纤维无挤压,如图 1所示.
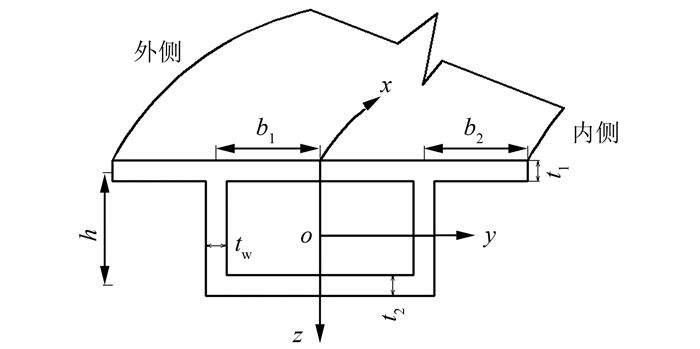
|
| 图 1 曲线箱梁截面形式 Fig. 1 Cross-section of curved box girder |
根据上述基本假定,曲线箱梁纵向剪力滞翘曲位移为
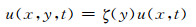 (1)
(1)
式中:u(x, t)为翼板剪切转角最大差值;ζ(y)为翘曲函数,分别假定其按下列分布:
1) 抛物线系列
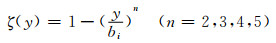 (2)
(2)
2) 余弦函数
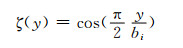 (3)
(3)
3) 指数函数
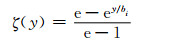 (4)
(4)
4) 悬链线
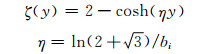 (5)
(5)
式(2)~(5)中:bi(i=1, 2)为箱梁翼板宽度的一半和悬臂板的宽度.
曲线箱梁在弯、扭、剪滞耦合作用下的线应变为
1) 正应变
腹板
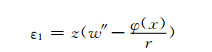 (6)
(6)
翼板
 (7)
(7)
2) 剪应变
腹板
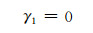 (8)
(8)
翼板
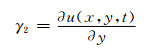 (9)
(9)
(6)~(9)中:w、φ(x)分别为箱梁竖向挠度和扭转角;r为曲率半径;hi为上下翼板到截面形心o的距离,各参数变量见图 1.
1.2 体系势能1) 腹板势能
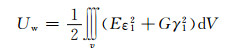 (10)
(10)
2) 翼板势能
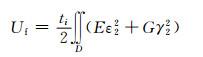 (11)
(11)
3) 自由扭转势能
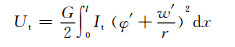 (12)
(12)
4) 约束扭转势能
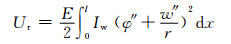 (13)
(13)
将式(2)~(9)代入式(10)~(13)并进行积分,得到曲线箱梁总的势能为
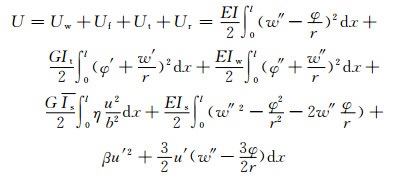 (14)
(14)
研究表明,引起剪力滞的本质在于产生了竖向弯曲变形或者有面内的剪切作用,因此当箱梁上下振动时,体系惯性力竖向振动动能为
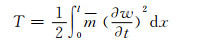 (15)
(15)
式(10)~(15)中:E、G为杨氏弹性模量和剪切模量;It、Iw分别为圣维南翘曲常数和扇形惯性矩; Is、Is分别为翼板惯性矩和翼板广义惯性矩,其中Is=(I1/b12+I2/b22)b2; l、m分别为曲线箱梁跨径和线质量密度.
1.3 振动微分方程设广义势能函数为
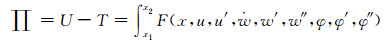 (16)
(16)
在小变形条件下,结构自由振动无外力势能,由Hamilton原理,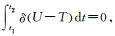
 (17)
(17)
式(17)即为薄壁曲线箱梁在各种剪翘位移模式下的振动控制微分方程,α、β、η均为剪力滞翘曲常数,括号数字和瞥表示对x的导数,点表示对时间t的导数.
由变分条件可知,式(17)相应的边界条件为
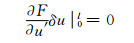 (18)
(18)
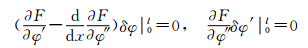 (19)
(19)
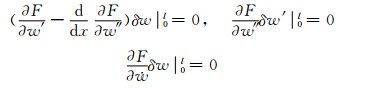 (20)
(20)
式(17)是相互耦联的高阶线性微分方程组,求解难度比较大,文献[4]给出了静载作用下的曲线箱梁剪力滞效应的闭合解,但公式复杂,计算量也比较大,本文将采用数值解法进行求解.
根据式(18)~(20)可得简支曲线箱梁几何边界条件为
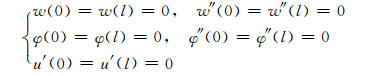 (21)
(21)
由边界条件并参考文献[1],可以合理假设曲线箱梁位移场函数为
 (22)
(22)
将式(22)求导后代入式(17)并进行整理得到:
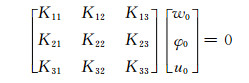 (23)
(23)
式(23)中,关于w0、φ0、u0的三元齐次方程组有非零解,故系数行列式为0,即
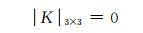 (24)
(24)
式中:
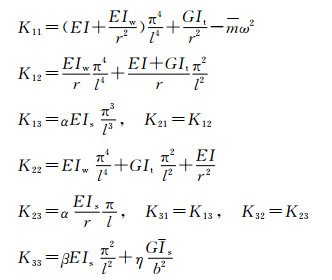
由此可以求得曲线箱梁振动基频为
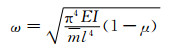 (25)
(25)
式中:
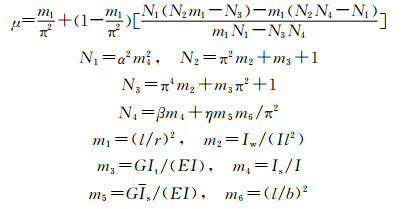
取文献[15]的曲线箱梁计算模型,力学参数为:E=3 000 MPa, ρ=1 180 kg/m3,参照图 1;几何参数为:b1=b2=100 mm,h=100 mm,t1=t2=tw=8 mm,r=2.5 m,l=1.309 m,在Matlab上编制计算程序,结果如表 1所示.
为验证理论公式推导的正确性,运用ANSYS建立曲线箱梁空间板壳有限元模型,采用4节点SHELL63单元,有限元模型如图 2所示,1阶竖弯振动频率为60.323 Hz.

|
| 图 2 有限元分析结果 Fig. 2 Results of finite element analysis |
由表 1和图 2可知,不同剪力滞翘曲函数下曲线箱梁自振基频相差不大,基于最小势能原理,当结构能量最小时,其对应的自振频率必然是最小的,因此可初步判断2次抛物线和悬链线是薄壁曲线箱梁合理的剪力滞翘曲位移函数.
本文理论计算结果与ANSYS板壳单元数值结果相比较,最大误差仅为0.57%,精度很高,而按《公路桥涵设计通用规范》计算的自振频率(基频)结果略微偏大,不宜直接用来计算车辆的冲击系数.
为进一步验证2次抛物线或悬链线是曲线箱梁剪力滞合理的翘曲位移函数,仍取文献[15]曲线箱梁模型,沿顶板与腹板相接处施加大小为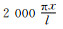

|
| 图 3 跨中截面顶板应力 Fig. 3 Stresses of upper flange at mid-span |

|
| 图 4 跨中截面底板应力 Fig. 4 Stresses of bottom flange at mid-span |
由图 3、4可知,无论是顶板还是底板,按能量变分法计算的曲线箱梁应力与ANSYS有限元分析最为接近的为悬链线和2次抛物线,尤其是在肋板交界处,悬链线、2次抛物线峰值与ANSYS最为相近,曲线走势基本一致,可以较好地反映箱梁的实际应力状态.
此外,在悬臂板自由端,本文计算结果与ANSYS均有较大的误差,这是由能量变分法自身缺陷所致.
再对各种剪力滞翘曲位移模式下的竖向挠度进行比较,图 5、6为薄壁曲线箱梁竖向位移云图和纵向应力云图,取跨中截面挠度进行分析,如表 2和图 7所示.

|
| 图 5 纵向应力云图 Fig. 5 Nephogram of longitudinal stresses |

|
| 图 6 竖向位移云图 Fig. 6 Nephogram of vertical displacements |
| 位移模式 | 挠度/mm | |
| 抛 物 线 |
2次 | 1.883 5 |
| 3次 | 1.878 8 | |
| 3次 | 1.871 2 | |
| 5次 | 1.846 1 | |
| 余弦函数 | 1.882 2 | |
| 指数函数 | 1.878 6 | |
| 悬链线 | 1.883 1 | |
| 有限元(板壳单元) | 1.979 1 | |

|
| 图 7 竖向挠度比较 Fig. 7 Comparation between vertical deflections |
由表 2和图 7可知,不同剪力滞翘曲位移模式下薄壁曲线箱梁跨中截面挠度结果相差不大,但就计算精度分析,与ANSYS分析结果最为接近的仍为2次抛物线和悬链线.
4 结论1) 基于能量变分法和Hamilton原理,通过理论推导、求解,给出了薄壁曲线箱梁竖向弯曲振动基频显示解,经与ANSYS有限元结果相比较,吻合良好,证明本文理论公式的推导是正确可靠的.
2) 采用《桥规》计算的薄壁曲线箱梁自振频率略微偏大,不宜直接用来计算车辆的冲击系数, 相比之下,本文方法具有更高的精度.
3) 薄壁曲线箱梁纵向剪力滞翘曲位移模式对其自振频率的影响较小.
4) 基于最小势能原理,对曲线箱梁自振频率、跨中截面应力、挠度的计算结果表明, 2次抛物线和悬链线是合理的剪力滞翘曲位移模式,具有更高的精度,可以较好地反映曲线箱梁空间力学性能.
5) 在用能量变分法进行薄壁曲线箱梁剪力滞计算时,建议优先选用2次抛物线和悬链线作为纵向剪力滞翘曲位移函数.
| [1] |
项海帆, 范立础. 高等桥梁结构理论[M]. 第2版. 北京: 人民交通出版社, 2013. Xiang Haifan, Fan Lichu. Advanced Theory of Bridge Structures[M]. 2nd Edition. Beijing: China Communication Press, 2013. |
| [2] |
孙璐, 王文雷, 吴国琦, 等. 客运专线箱梁端部裂纹成因分析及施工控制[J]. 铁道工程学报, 2007, 24(10): 44-49. Sun Lu, Wang Wenlei, Wu Guoqi, et al. Analyses of the causes for crack on the end side of box girder for railway passenger dedicated line and its construction control[J]. Journal of Railway Engineering Society, 2007, 24(10): 44-49. DOI:10.3969/j.issn.1006-2106.2007.10.011 |
| [3] |
张元海, 李琳, 林丽霞, 等. 以附加挠度作为广义位移时薄壁箱梁剪力滞效应的梁段有限元分析[J]. 土木工程学报, 2013, 46(10): 100-107. Zhang Yuanhai, Li Lin, Lin Lixia, et al. Beam-segment finite element analysis on shear lag effect of thin-walled box girder adopting additional deflection as generalized displacement[J]. China Civil Engineering Journal, 2013, 46(10): 100-107. |
| [4] |
罗旗帜.基于能量原理的薄壁箱梁剪力滞理论分析与试验研究[D].长沙: 湖南大学, 2005. Luo Qizhi. Theory and model test studies of the shear lag in thin walled box girders based on energy principle[D]. Changsha: Hunan University, 2005. |
| [5] |
Zhou Wangbao, Jiang Lizhong, Liu Zhijie, et al. Closed-form solution to thin-walled box girders considering effects of shear deformation and shear lag[J]. Journal of Central South University (English Edition), 2012, 19(9): 2650-2655. DOI:10.1007/s11771-012-1323-8 |
| [6] |
冀伟, 刘世忠, 蔺鹏臻. 波形钢腹板PC连续箱梁桥自振频率分析与试验研究[J]. 中南大学学报(自然科学版), 2016, 47(4): 1297-1304. Ji Wei, Liu Shizhong, Lin Pengzhen. Analysis and experimental study on nature vibration frequencies of PC continuous box girder bridge with corrugated steel webs[J]. Journal of Central South University(Natural Science Edition), 2016, 47(4): 1297-1304. |
| [7] |
甘亚南, 周广春. 基于能量变分原理的薄壁箱梁自振特性分析[J]. 中国公路学报, 2007, 20(1): 73-78. Gan Yanan, Zhou Guangchun. Analysis of free vibration characteristics of thin walled box girder based on energy variation principle[J]. China Journal of Highway and Transport, 2007, 20(1): 73-78. DOI:10.3321/j.issn:1001-7372.2007.01.014 |
| [8] |
甘亚南, 周广春. 薄壁箱梁纵向剪滞翘曲函数精度选择的研究[J]. 工程力学, 2008, 25(6): 100-106. Gan Yanan, Zhou Guangchun. An approach for precision selection of longitudinal shear lag warping displacement function of thin-walled box girders[J]. Engineering Mechanics, 2008, 25(6): 100-106. |
| [9] |
周旺保, 蒋丽忠, 戚菁菁. 考虑剪力滞和剪切变形的薄壁箱梁自振特性分析[J]. 计算力学学报, 2013, 30(6): 802-806. Zhou Wangbao, Jiang Lizhong, Qi Jingjing. Analysis of free vibration characteristic of thin-walled box-girder considering shear lag and shear deformation[J]. Chinese Journal of Computational Mechanic, 2013, 30(6): 802-806. |
| [10] |
JTG D60-2015公路桥涵通用设计规范[S].北京: 人民交通出版社, 2015. JTG D60-2015 General Specifications for Design of Highway Bridges and Culverts[S]. Beijing: China Communications Press, 2015. |
| [11] |
张元海, 林丽霞. 薄壁箱梁剪力滞效应分析的初参数法[J]. 工程力学, 2013, 30(8): 205-211. Zhang Yuanhai, Lin Lixia. Initial parameter method for analyzing shear lag effect of thin-walled box girders[J]. Engineering Mechanics, 2013, 30(8): 205-211. |
| [12] |
蔺鹏臻, 刘凤奎, 冀伟. 变分原理分析混凝土箱梁的剪力滞效应[J]. 铁道学报, 2013, 35(2): 93-98. Lin Pengzhen, Liu Fengkui, Ji Wei. Analysis on shear lag effect of concrete box beam by variational principle[J]. Journal of the China Railway Society, 2013, 35(2): 93-98. DOI:10.3969/j.issn.1001-8360.2013.02.014 |
| [13] |
张玉红.薄壁箱梁剪力滞效应的理论分析与试验研究[D].兰州: 兰州交通大学, 2011. Zhang Yuhong. The experimental study and theoretical analysis in shear lag effect on thin-walled box-girder[D].Lanzhou: Lanzhou Jiaotong University, 2011. |
| [14] |
何黎, 陈世民. 常截面悬臂箱形梁负剪力滞效应分析[J]. 成都大学学报, 2011, 30(1): 40-43. He Li, Chen Shimin. Analysis of negative shear lag effect in cantilever box girder with constant depth[J]. Journal of Chengdu University, 2011, 30(1): 40-43. |
| [15] |
卢海林, 蔡恒, 汤正. 移动荷载作用下薄壁曲线箱梁剪力滞效应分析[J]. 铁道建筑, 2016(9): 14-18. Lu Hailin, Cai Heng, Tang Zheng. Analysis of shear lag effect of thin-walled curved box girder under moving load[J]. Railway Engineering, 2016(9): 14-18. DOI:10.3969/j.issn.1003-1995.2016.09.04 |
 2019, Vol. 52
2019, Vol. 52




