文章信息
- 肖俊, 周勇, 韩彦辉, SARHOSISVasilis, 王涛
- XIAO Jun, ZHOU Yong, HAN Yanhui, SARHOSIS Vasilis, WANG Tao
- 基于三维离散单元法庞贝古城柱廊的动力特性分析
- Seismic responses of Pompeii colonnade structure based on three-dimensional distinct element method
- 武汉大学学报(工学版), 2018, 51(8): 688-694, 702
- Engineering Journal of Wuhan University, 2018, 51(8): 688-694, 702
- http://dx.doi.org/10.14188/j.1671-8844.2018-08-004
-
文章历史
- 收稿日期: 2017-04-21
2. 湖北省水利水电科学研究院, 湖北 武汉 430072;
3. 中国电建集团华东勘测设计研究院有限公司,浙江 杭州 310014;
4. 中国矿业大学(北京)力学与建筑学院, 北京 100083;
5. 纽卡斯尔大学,英国 纽卡斯尔 NE1 7RU
2. Hubei Water Resources Research Institute, Wuhan 430072, China;
3. Power China Huadong Engineering Corporation Limited, Hangzhou 310014, China;
4. School of Mechanics and Civil Engineering, China University of Mining & Technology, Beijing 100083, China;
5. Newcastle University, Newcastle Upon Tyne, NE1 7RU, UK
古建筑文物具有重要的历史、文化、科学价值,是人类社会的珍贵遗产和重点保护对象.在漫长的历史岁月中,由于遭受动力荷载、水盐侵蚀、风化和温度应力等自然营力的作用,古建筑文物结构的完整性和稳定性严重降低.我国是一个多地震国家,地震对抗震能力较弱的古建筑文物具有灾难性的作用,目前国内关于古建筑文物的动力响应特性研究主要集中在古木结构[1-3]、砖石古塔[4-6]、岩凿石窟[7, 8]等,极少涉及到古典柱廊类型的古建筑文物的动力响应特性研究.
柱廊是西方建筑自古就广泛采用的建筑元素之一,它以丰富多彩的形态存在于各类建筑、建筑群以及城市空间中.古典柱廊是由多个鼓状石块相互堆叠而成,石块之间没有粘结物质却高度贴合.这种不连续的柱状结构会导致石柱在地震作用下产生摆动和滑移的破坏模式,进而使柱廊的动力响应呈现出复杂的非线性特征.因此,解析方法难以解决这类结构的动力响应问题.一些国外学者通过物理试验方法研究由金属[9, 10]、石膏[11]等材料制作的小尺寸柱廊模型的动力响应,结果表明刚体的晃动具有尺寸效应,只有真实尺寸模型的试验结果是可靠的.但是全尺寸模型的物理试验是难以操作和控制的,也会花费大量的人力和物力.
随着计算机技术的飞速发展,数值模拟方法提供了一种理想高效的途径来研究这种结构复杂文物的动态响应特征.尽管有限单元法(FEM)可以通过界面单元处理一些不连续体问题[12],但是在不连续面较多或位移太大的情况下,这类方法会失去作用.离散单元法(DEM)由Cundall等[13]于1971年提出,是一种可以专门用来解决不连续介质问题的数值模拟方法,它适用于研究大变形、非线性、非连续性的问题,离散体可以发生平移和旋转,甚至研究对象之间可以发生完全脱离[14].许多国外学者已经运用离散单元法研究堆石结构的静态和动态问题,并取得了诸多有价值的成果.Psycharis等[15]采用二维离散元软件UDEC研究了平面内古典柱廊的动力响应并确定了影响柱廊稳定的主要因素,发现地震卓越周期越大,对柱廊结构的威胁越大;Papantonopoulos等[16]利用离散元方法预测大理石古典柱廊的三维动力响应,并与Mouzakis等[11]的试验数据进行对比,验证了离散单元法的有效性;Sarhosis等[17]采用UDEC模拟了位于意大利庞贝古城的2层柱廊的静态和动态稳定性,结果表明低频率动力荷载主要产生晃动效应,高频率动力荷载会同时产生滑动和晃动现象.虽然二维模拟能够揭示平面内柱廊结构动力响应的一般规律,但不能反映真实情况下平面外动力荷载的影响,而且这种影响显然是非常重要的.和三维模拟相比,二维模拟由于缺少平面外的动力荷载会表现出更好的稳定性,不能全面反映真实的破坏模式.因此,三维模拟对于研究这种2层柱廊结构在平面内和平面外的动力响应是很有必要的.
本文是在前期与英国纽卡斯尔大学(Newcastle University)关于文物保护合作研究的基础上开展,其中的计算部分主要由中方研究人员完成,二维离散元计算成果已经于2016年发表(Bulletin of Earthquake Engineering, 2016, 14(4): 1131-1152).本文采用三维离散元程序3DEC分析了意大利庞贝古城的柱廊结构在简谐波和实测地震波作用下的动力响应,研究了波的频率及加速度对该柱廊结构的影响规律,探索了柱廊结构地震动力响应的研究方法.意大利的庞贝古城和我国的龙门石窟一样,均被联合国教科文组织列入《世界遗产名录》.从文物保护的角度来看,两者同为大型露天文物遗址[18],在文物病害和保护方法上有诸多相通之处.因此本文的研究方法和结果可为我国大型露天文物遗址的抗震保护提供参考.
庞贝古城位于意大利南部那不勒斯附近,维苏威火山西南脚下10 km处.据地质学家们考证,维苏威火山是一座典型的活火山,数千年来它一直在不断喷发,因此古城遗迹面临着较大的地震风险.本文研究的柱廊结构是庞贝古城的部分遗迹,始建于公元前6世纪,在公元79年,整个柱廊被重新建造,用石灰岩代替了原本的凝灰岩石材.1980年,遗址附近发生了地震,对柱廊产生了一定的破坏,与该柱廊结构相连的其他结构倒塌,而位于该柱廊结构上层石柱上的横梁被移走,剩下了现今的结构.图 1是本文要研究的庞贝古城柱廊结构的实际构造,它是一个双层的柱廊结构,由上、下两层石柱和中部的横梁组成.石柱是由多个圆柱形石块竖向堆叠而成,石块之间的接触面贴合程度很高,中间没有粘结材料.横梁是由不规则的六面体石块横向支撑而成,横梁中不受石柱支撑的石块能够在两侧横梁石块的支撑下保持稳定.
3DEC中离散元块体的运动方式由作用在其上的不平衡力和不平衡力矩所决定,表现为块体的平移和围绕其形心的转动.块体运动满足牛顿第二定律,即
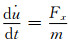 (1)
(1)
进行中心差分,则
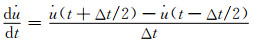 (2)
(2)
速度方程变为
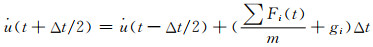 (3)
(3)
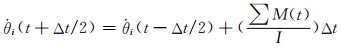 (4)
(4)
引入阻尼后,动力学基本方程为
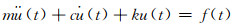 (5)
(5)
式中:ü为单元加速度;
对于动力问题3DEC采用动态松弛求解方法,对于非线性问题,该方法的实质是将临界阻尼振动方程逐步积分.采用中心差分法进行动态松弛求解,不需要解大型矩阵,并且允许单元发生较大的平移和转动,克服了有限单元法和边界单元法的小变形假设.
在动力分析中,阻尼需要再现对象在承受动力荷载作用下,系统能量的损失.对于岩石这种材料,自然阻尼一般情况下是滞后的,与路径相关,因此很难用数值方法再现这种阻尼.3DEC中用本构方程表征这种滞后性,提供了局部阻尼和瑞利阻尼供选择,在动力计算中使用瑞利阻尼更加符合本文的实际情况.
进行动力计算时,为避免模型过大导致计算时间太长,动力荷载可直接施加在研究对象之上,但是由于边界过小,会导致入射波在边界发生反射,从而不利于能量的耗散而导致模拟结果失真.为了解决该问题,3DEC中采用了自由场边界(Free-Field Boundary)和粘滞边界(Viscous Boundary).粘性边界是由Lysmer和Kuhlemeyer[20]在1969年提出的,其基本做法是在模型边界的法向及切向分别设置阻尼器以吸收入射波.自由场边界是通过侧向边界与自由场网格产生耦合,将自由场节点的不平衡力加到主体的网格边界上.
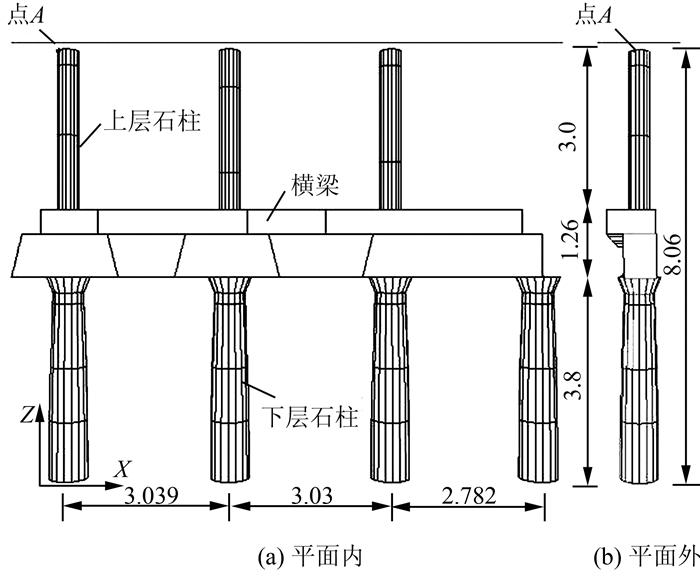
2 计算过程 2.1 几何模型采用3DEC程序,建立了该双层柱廊结构的几何模型.模型及其尺寸见图 2.块体采用各向同性弹性模型,节理采用库仑滑动模型.三维计算模型的规模为:块体数38,单元数3 948,块体接触数为44.
|
| 图 2 柱廊结构的离散元计算模型(单位:m) Figure 2 DEM model of the two-story colonnade of the Forum in Pompeii (unit:m) |
由于庞贝古城是意大利重点保护的文物古迹,因此无法直接在柱廊上进行测试.本文参考Kastenmeier等[21]和Angrisani等[22]在类似的石块和节理上做的实验结果,相应的参数取值见表 1、2.考虑到实际的柱廊结构是由多块石材堆积上去的,石块间没有任何的粘结材料,故节理抗拉强度、节理粘聚力以及剪胀角都取为0.
| 密度/(kg·m-3) | 弹性模量/GPa | 剪切模量/GPa | 体积模量/GPa | 泊松比/υ |
| 2 680 | 40 | 16 | 27 | 0.25 |
| 节理法向刚度/(GPa·mm-1) | 节理切向刚度/(GPa·mm-1) | 节理摩擦角/(°) | 节理抗拉强度/MPa | 粘聚力/MPa | 剪胀角/(°) |
| 4 | 2 | 36.8 | 0 | 0 | 0 |
首先进行静力计算,柱廊的左右边界及上部设为自由边界,底部固定,模型在自重作用下达到平衡.接着进行动力计算,底部施加粘性边界,动力荷载施加在模型的底部边界上.为便于分析计算结果,特别是位移和速度的动力响应,在模型上布置了监测点.见图 2所示的结点A.监测结点A在整个过程中(包括在自重作用下的静力平衡阶段,施加动力荷载的动力响应阶段以及动力结束后的平衡阶段)的速度、位移变化情况.
2.4 简谐波响应简谐波波形有规律,计算时间短,有利于初步分析柱廊在波作用下的动力特性,也便于与后面实测地震波的计算结果进行对比,验证实测地震波得出结论的合理性.在参数研究中,简谐波频率范围是1~7 Hz,加速度幅值范围是1.7~70 m/s2.在不同频率简谐波作用下,柱廊结构发生破坏所需要的简谐波加速度幅值是不同的.在计算过程中,每个频率的简谐波的加速度幅值逐步增加至70 m/s2,由此可以判断柱廊结构在不同频率、不同加速度幅值水平简谐波作用下是否破坏,进而确定各频率简谐波的破坏临界加速度幅值.
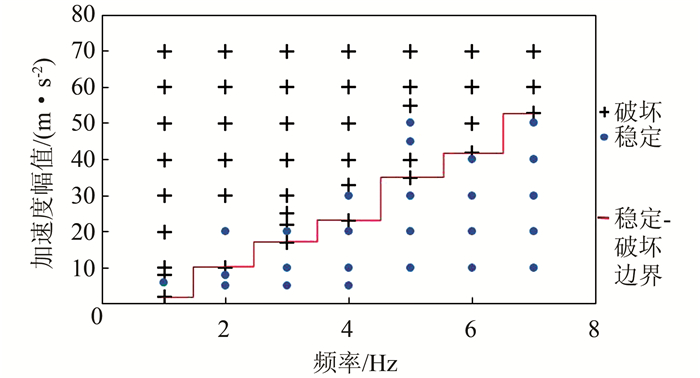
如图 3所示(X方向施加简谐波),在每一对频率与加速度幅值的组合作用下,结构是否破坏在图中清楚地表示出来,加速度幅值必须大于临界值才可能发生破坏,据此可以做出结构稳定-破坏的边界线.在很多情况下,柱廊在某一个加速度幅值下发生破坏,而在更大的加速度幅值作用下未发生破坏.此时,稳定与破坏的临界加速度幅值应取为柱廊首次发生破坏时的加速度幅值.从图 3可以看出,稳定-破坏边界线呈现阶梯上升之势,说明频率越高,所需的破坏加速度幅值越大,或者说频率越低,所需的破坏加速度幅值越小,即低频简谐波比高频简谐波更容易引起柱廊结构发生破坏.

|
| 图 3 在X方向施加简谐波时的稳定-破坏边界 Figure 3 Safe-unsafe boundary under harmonic wave applied in X-direction |
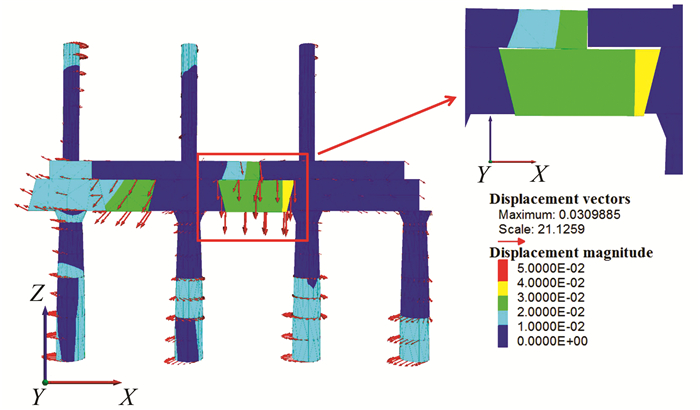
图 4所示为频率7 Hz、加速度幅值为60 m/s2条件下简谐波作用后柱廊结构发生破坏时的位移云图(包含位移矢量),石块之间的位移响应差异显著,体现出柱廊结构的非线性、非连续性特征,这是由于石块之间没有粘结强度导致的.通过对比不同加速度幅值作用下柱廊结构的位移云图,发现较大的加速度幅值会导致较大的结构位移.此外,位移较大的石块主要分布在横梁和下层石柱,位移最大值出现在横梁底层中间的石块,如图 4中方框所示的部位,该石块由于处于横梁的跨中部位,没有竖向石柱的支撑,因此在地震作用下会产生较大位移.下层石柱的位移普遍比上层石柱大,说明横梁会削弱向上传播的动力荷载.这些规律与二维动力响应规律[17]吻合.
|
| 图 4 频率7 Hz加速度幅值60 m/s2下的廊柱的位移云图及位移矢量图 Figure 4 Contours and vectors of displacement magnitude of the colonnade under frequency of 7 Hz and acceleration of 60 m/s2 |
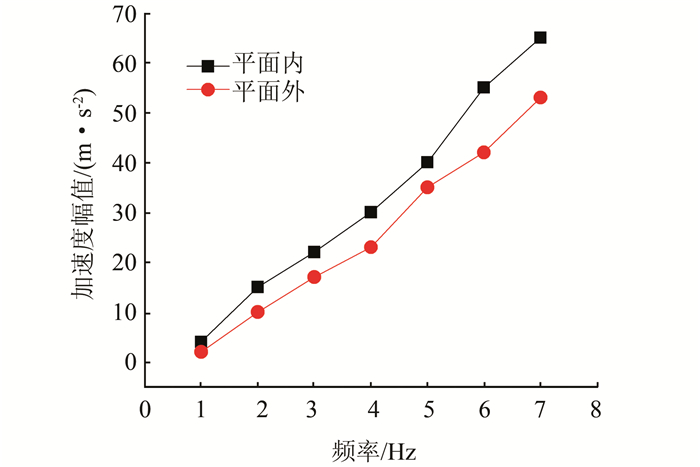
与二维模拟相比,三维模拟方法可以研究柱廊结构平面外荷载的动力响应.在平面外方向(Y轴方向)单独施加简谐波荷载,频率为1~7 Hz,加速度幅值为1.7~70 m/s2.采用同样的加载方案,所得结果如图 5所示.由此可见,平面外和平面内简谐波作用下的临界加速度幅值随频率的变化规律是一致的,但影响程度存在明显差异.图 6将2种情况的临界加速度幅值进行了比较,可见在平面外和平面内2个方向上分别施加相同频率的简谐波,后者引起结构发生破坏的加速度幅值要大一点,说明柱廊结构对平面外荷载的抵抗力较弱,即平面外荷载的破坏作用比平面内荷载更显著.
|
| 图 5 在Y方向施加简谐波时的稳定-破坏边界 Figure 5 Safe-unsafe boundary under harmonic wave applied in Y-direction |
|
| 图 6 X和Y方向上均施加简谐波时的临界加速度值的对比图 Figure 6 Comparison of critical X- and Y-accelerations in harmonic waves |
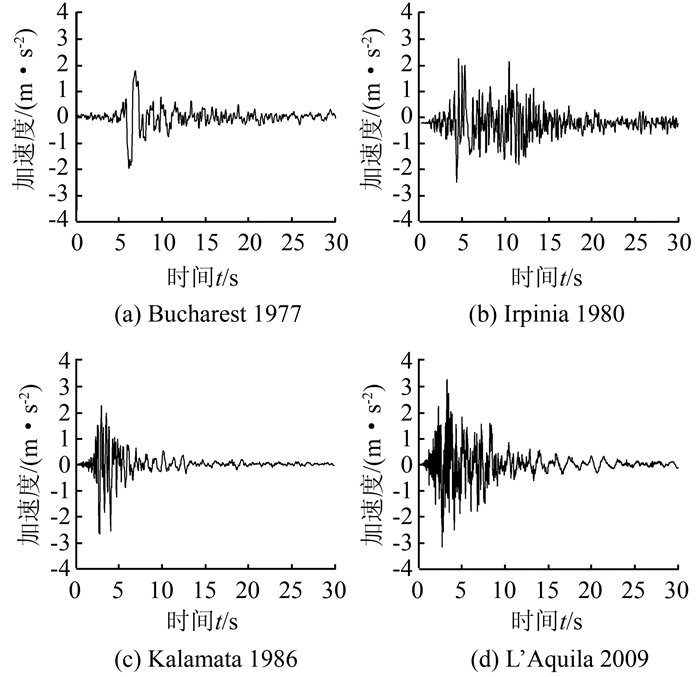
在前面的简谐波动力分析的基础上,可以进一步地研究真实地震波是如何影响该柱廊结构的.选取了4个具有不同特点(如震级、卓越周期、频率等)的地震波,分别是:Bucharest 1977,Irpinia 1980,Kalamata 1986和L'Aquila 2009.相应的波形(在相同的时间和加速度范围内绘出)见图 7,特点见表 3.
|
| 图 7 4种地震波加速度时程曲线 Figure 7 Four kinds of seismic acceleration time history curves |
| 地震波 | 发生地 | 震级 | 卓越周期/s |
| Bucharest 1977 | 布加勒斯特 | 7.2 | 1.2 |
| Irpinia 1980 | 伊尔皮尼亚 | 6.9 | 0.37 |
| Kalamata 1986 | 卡拉马塔 | 6.2 | 0.32 |
| L'Aquila 2009 | 拉奎拉 | 6.3 | 0.5 |
每个地震波经过SeismoSignal软件处理,保持频率不变,将地震波的峰值加速度按比例逐渐扩大,得到了一系列具有不同加速度幅值的地震波.分别在柱廊底部平面内(X方向)和平面外(Y方向)施加经过处理的地震波,研究地震波的频率以及峰值加速度对双层柱廊结构的影响规律.
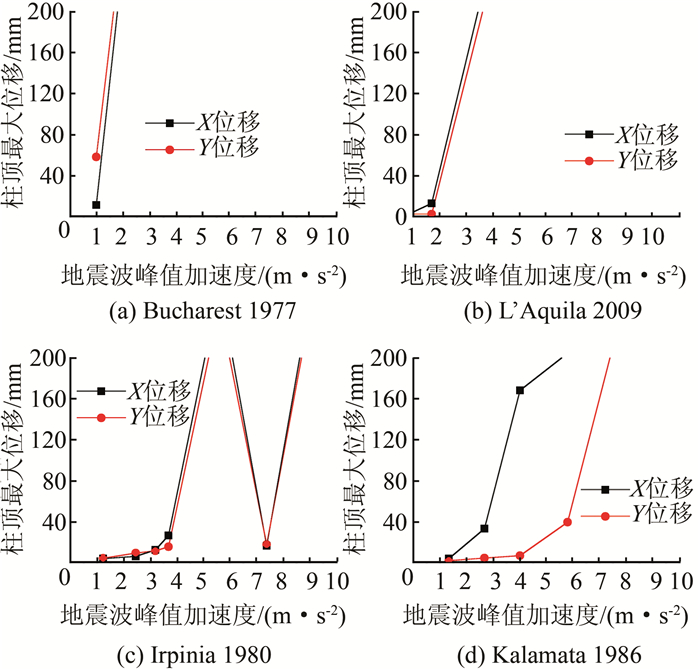
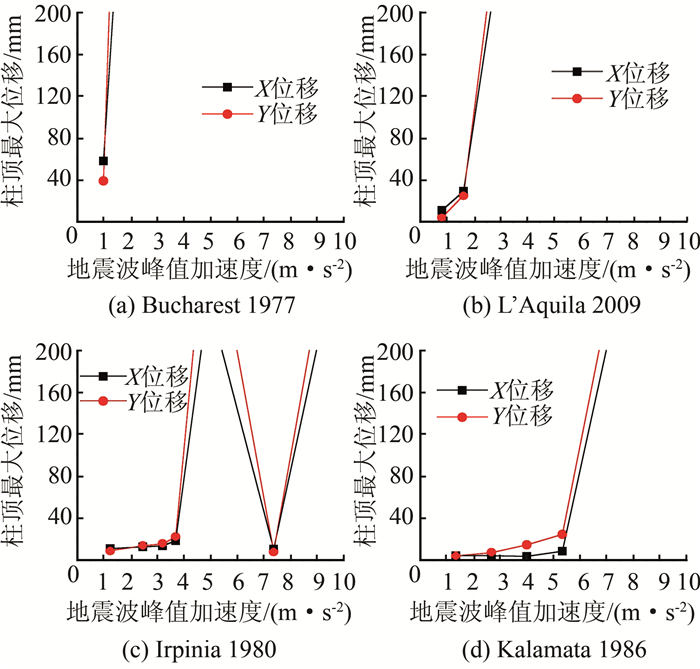
图 8表示在X方向上施加地震波,柱廊结构最左端柱顶结点A(图 2)的最大X和Y位移情况,图 9是在Y方向上施加地震波的情况.分析图 8、9可以得出,在柱廊结构首次发生破坏之前,地震波的峰值加速度越大,柱顶点A的位移值越大.值得注意的是,柱廊结构在某个加速度下发生了破坏,但在更大的加速度下可能仍然稳定.在地震波Irpinia 1980作用下(图 8),峰值加速度为5 m/s2时,结构已经发生了破坏,而峰值加速度为7.5 m/s2时,却仍然保持稳定.比较图 8、9中X、Y方向上的位移可以发现,施加荷载的方向上产生的位移大部分大于未施加荷载的方向,平面外(Y方向)施加荷载产生的X和Y方向的位移差距(图 9)要小于在平面内(X方向)施加荷载产生的位移差距(图 8).
|
| 图 8 在X方向施加地震波A点的X和Y方向位移 Figure 8 The maximum X- and Y-displacement at point A versus peak input accelerations under seismic loading in X-direction |
|
| 图 9 在Y方向施加地震波A点的X和Y方向位移 Figure 9 The maximum X- and Y-displacement at point A versus peak input acceleration under seismic loading in Y-direction |
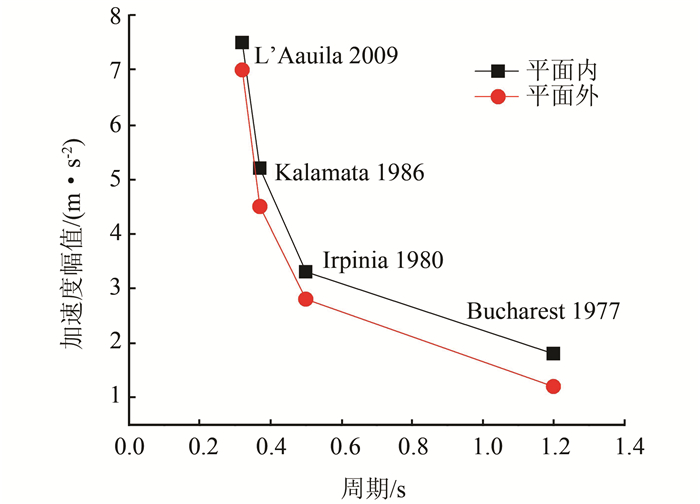
与简谐波一样,可以分析地震波的周期对柱廊结构的影响.如图 8所示(X方向施加地震荷载),柱廊结构在地震波Bucharest 1977作用下,峰值加速度为1.5 m/s2时就发生了破坏,Bucharest 1977的卓越周期最大,为1.20 s.对于地震波L'Aquila 2009,其卓越周期大约为0.50 s,峰值加速度为3 m/s2时,结构发生破坏,廊柱破坏时3DEC的计算结果如图 10所示.至于地震波Irpinia 1980和Kalamata 1986,卓越周期分别为0.37、0.32 s左右,相应的结构发生破坏时的峰值加速度应该比前两者更大些.计算结果也是如此:Irpinia 1980在加速度为5 m/s2左右时,结构发生破坏;Kalamata 1986则在7 m/s2左右时才发生破坏.由此可以得出,柱廊结构在卓越周期较大的地震波作用下,更容易发生破坏,这与简谐波动力响应规律是一致的.图 11比较了分别在X、Y方向施加这4个地震波的临界峰值加速度,结果表明在同一地震作用下,平面外(Y方向)施加荷载产生的临界峰值加速度均低于平面内(X方向)施加荷载产生的临界峰值加速度,说明平面外的荷载更容易导致柱廊结构发生破坏.

|
| 图 10 廊柱在地震波L'Aquila 2009作用下的破坏情况 Figure 10 The destruction of the colonnade under seismic wave L'Aquila 2009 |
|
| 图 11 X和Y方向上均施加地震波时的临界峰值加速度的对比图 Figure 11 Comparison of critical X- and Y-accelerations in seismic waves |
本文采用3DEC对意大利庞贝古城的柱廊结构进行了三维建模,分析了其在简谐波和实测地震波作用下的动力响应,研究了波的不同频率、加速度幅值以及荷载施加的方向下该柱廊结构的动力响应规律,得到了以下结论:
1) 在简谐波作用下,柱廊结构的变形随着加速度幅值的增加而变大,低频波比高频波更容易导致柱廊结构发生破坏,位移较大的部位出现在横梁和下层石柱,横梁可以削弱向上传播的动力荷载.
2) 在4种具有不同特征的地震波作用下,不同加速度幅值和频率下柱廊结构的动力响应规律与简谐波动力响应规律基本一致.
3) 无论在简谐波还是在地震波作用下,柱廊结构在平面外方向的抗震能力低于平面内方向,即柱廊结构在平面外的方向更容易发生破坏.
| [1] |
李铁英, 魏剑伟, 张善元, 等. 应县木塔实体结构的动态特性试验与分析[J].
工程力学, 2005, 22(1): 141–146.
Li Tieying, Wei Jianwei, Zhang Shanyuan, et al. Experiment and analysis of vibration characteristics of Yingxian Wooden Tower[J]. Engineering Mechanics, 2005, 22(1): 141–146. DOI:10.3969/j.issn.1000-4750.2005.01.025 |
| [2] |
李铁英, 魏剑伟, 李世温, 等. 应县木塔扭转振动特性和地面强迫振动试验与分析[C]//第16届全国结构工程学术会议论文集(第Ⅲ册). 北京: 清华大学出版社, 2007: 357-364.
Li Tieying, Wei Jianwei, Li Shiwen, et al. The experiment and analysis of the twist vibration characteristics and forced vibration of Yingxian Wooden Tower[C]// Proceedings of the 16th National Conference on Structural Engineering (Section Ⅲ). Beijing: Tsinghua University Press, 2007: 357-364. |
| [3] |
李铁英, 严旭, 魏剑伟, 等. 应县释迦塔扭转振动特性和地面周期性强迫振动试验与分析[J].
太原理工大学学报, 2008, 39(5): 519–522.
Li Tieying, Yan Xu, Wei Jianwei, et al. The experiment and analysis of the twist vibration characteristics and forced vibration of Yingxian Shijia Tower[J]. Journal of Taiyuan University of Technology, 2008, 39(5): 519–522. |
| [4] |
李德虎, 魏琏. 砖石古塔的历史震害与抗震机制[J].
建筑科学, 1990(1): 13–18.
Li Dehu, Wei Lian. Historical earthquake disaster and the seismic resistance mechanism of masonry pagodas[J]. Building Science, 1990(1): 13–18. |
| [5] |
卢俊龙, 姚谦峰, 张荫. 砖石古塔的抗震机制及加固对策研究[C]//第七届全国地震工程学术会议论文集. 北京: 地震出版社, 2006: 1184-1189.
Lu Junlong, Yao Qianfeng, Zhang Yin, et al. The seismic resistance mechanism and strengthening countermeasures of masonry pagodas[C]// Proceedings of the 7th National Earthquake Engineering Academic Conference. Beijing: Earthquake Press, 2006: 1184-1189. |
| [6] |
姚谦峰, 卢俊龙, 张荫. 砖石古塔抗震加固对策探讨[J].
工业建筑, 2007, 37(9): 115–118.
Yao Qianfeng, Lu Junlong, Zhang Yin, et al. The seismic resistance mechanism and strengthening countermeasures of masonry pagodas[J]. Industrial Architecture, 2007, 37(9): 115–118. |
| [7] |
孙博, 彭宁波, 王逢睿. 云冈石窟第19窟西耳窟地震动力响应[J].
西南交通大学学报, 2012, 47(4): 573–579.
Sun Bo, Peng Ningbo, Wang Fengrui. Seismic dynamic responses of No.19 Grotto's West Side Cave of Yungang Grottoes[J]. Journal of Southwest Jiaotong University, 2012, 47(4): 573–579. DOI:10.3969/j.issn.0258-2724.2012.04.006 |
| [8] |
唐智亮. 固结灌浆在保护云岗石窟石质文物遗址的应用研究[D]. 长春: 吉林大学, 2013.
Tang Zhiliang. Consolidation grouting stone in the protection of cultural heritage sites of Yungang Grottoes research[D]. Changchun: Jilin University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10183-1014129984.htm |
| [9] | Demosthenous M, Manos G C. Study of the dynamic response of models of ancient columns or colonnades subjected to horizontal base motions[J]. Struct Dyn-eurodyn, 1996(2): 841–848. |
| [10] | Manos G C, Demosthenous M, Kourtides V, et al. Dynamic and earthquake behavior of models of ancient columns and colonnades with or without energy absorbtions systems[C]//Proceedings of Second Greek National Conference on Earthquake Engineering and Seismology. 2001, 1: 257-276. |
| [11] | Mouzakis H P, Psycharis I N, Papastamatiou D Y, et al. Experimental investigation of the earthquake response of a model of a marble classical column[J]. Earthquake Engineering & Structural Dynamics, 2002, 31(9): 1681–1698. |
| [12] | Mitsopoulou E, Doudoumis I N, Paschalidis V. Numerical analysis of the dynamic seismic response of multi-block monumental structures[C]// 11th European Conference on Earthquake Engineering, 1998: 1-13. |
| [13] | Cundall P A. A computer model for simulating progressive large-scale movements in blocky rock systems[C]// Proceedings of Symposium of Rock Mechanics, 1971, Ⅱ: 129-136. |
| [14] | Cundall P A, Strack O D L. A discrete numerical model for granular assembles[J]. Geotechnique, 1979, 29(1): 47–65. DOI:10.1680/geot.1979.29.1.47 |
| [15] | Psycharis I N, Papastamatiou D Y, Alexandris A P. Parametric investigation of the stability of classical columns under harmonic and earthquake excitations[J]. Earthquake Engineering & Structural Dynamics, 2000, 29(8): 1093–1109. |
| [16] | Papantonopoulos C, Psycharis I N, Papastamatiou D Y, et al. Numerical prediction of the earthquake response of classical columns using the distinct element method[J]. Earthquake Engineering & Structural Dynamics, 2002, 31(9): 1699–1717. |
| [17] | Sarhosis V, Asteris P, Wang T, et al. On the stability of colonnade structural systems under static and dynamic loading conditions[J]. Bulletin of Earthquake Engineering, 2016, 14(4): 1131–1152. DOI:10.1007/s10518-016-9881-z |
| [18] |
李心坚, 李随森. 从意大利庞贝古城坍塌事故看龙门石窟的保护[J].
丝绸之路, 2011(12): 93–95.
Li XinJian, Li Suisen. Talking Longmen Grottoes protection from Pompeii Collapse[J]. The Silk Road, 2011(12): 93–95. DOI:10.3969/j.issn.1005-3115.2011.12.037 |
| [19] |
王泳嘉, 邢纪波.
离散元法及其在岩土力学中的应用[M]. 沈阳: 东北大学出版社, 1991.
Wang Yonjia, Xing Jibo. The Discrete Element Method and Application in Rock and Soil Mechanics[M]. Shenyang: Northeast University Press, 1991. |
| [20] | Lysmer J, Kuhlemeyer R L. Finite dynamic model for infinite media[J]. Journal of the Engineering Mecha-nics Division, 1969, 95(4): 859–878. |
| [21] | Kastenmeier P, Di Maio G, Balassone G, et al. The source of stone building materials from the Pompeii archaeological area and its surroundings[J]. Periodico di Mineralogia, 2010, 79: 39–58. |
| [22] | Angrisani A C, Calcaterra D, Colella A, et al. Stone properties and weathering phenomena of the Miocene Cusano Limestones (aka Perlato Royal Coreno): the case of the basement of the Santa Chiara Monastery bell tower (Naples-Italy)[J]. Periodico di Mineralogia, 2010, 79: 1–10. |
 2018, Vol. 51
2018, Vol. 51





