武汉大学学报(工学版)   2017, Vol. 50 Issue (2): 245-250

文章信息

章杨帆, 刘涤尘, 梁姗姗, 彭昌勇
ZHANG Yangfan, LIU Dichen, LIANG Shanshan, PENG Changyong
考虑励磁和调速器系统的水电机群等值建模
An equivalent modeling for hydropower generator group considering excitation and governor system
武汉大学学报(工学版), 2017, 50(2): 245-250
Engineering Journal of Wuhan University, 2017, 50(2): 245-250
http://dx.doi.org/10.14188/j.1671-8844.2017-02-014

文章历史

收稿日期: 2016-06-10
 Abstract              PDF               Figures               Tables
引用本文 0
章杨帆, 刘涤尘, 梁姗姗, 彭昌勇. 考虑励磁和调速器系统的水电机群等值建模[J]. 武汉大学学报(工学版), 2017, 50(2): 245-250.
ZHANG Yangfan, LIU Dichen, LIANG Shanshan, PENG Changyong. An equivalent modeling for hydropower generator group considering excitation and governor system[J]. Engineering Journal of Wuhan University, 2017, 50(2): 245-250.
考虑励磁和调速器系统的水电机群等值建模
章杨帆1, 刘涤尘1, 梁姗姗1, 彭昌勇2     
1. 武汉大学电气工程学院，湖北 武汉 430072;
 2. 湖北省电力公司经济技术研究院，湖北 武汉 430062
收稿日期：2016-06-10
作者简介：章杨帆(1990-)，男，硕士研究生，研究方向为电力系统安全稳定分析与控制, E-mail:zhangyangfan_007@sina.com.
通讯作者：刘涤尘(1953-)，男，教授，博士生导师，研究方向为电力系统稳定与控制、电力自动监测技术等, E-mail:dcliu@whu.edu.cn
基金项目：国家电网公司重点科技项目(编号：52153813020D).
摘要：对中小水电机群进行等值建模是对含水电的电网进行动态分析时的一种实用方法，励磁和调速器系统对等值模型的精度具有突出影响.提出了含励磁和调速系统的中小水电机群等值建模方法，该方法以传统的基于同调法的水电机群等值模型为基础，考虑励磁与调速器系统的等值，采用PLPF法得到励磁系统的等值参数，采用加权平均法得到原动机及调速器的等值参数.算例表明该方法在动态过程的误差较小，能够提高仿真精度.在此基础上，进一步分析了励磁和调速器系统对动态特性的影响.
关键词：水电机群    动态等值    励磁系统    PLPF法    调速器    
An equivalent modeling for hydropower generator group considering excitation and governor system
ZHANG Yangfan1, LIU Dichen1, LIANG Shanshan1, PENG Changyong2     
1. School of Electrical Engineering, Wuhan University, Wuhan 430072, China;
 2. Economic Research Institute, Hubei Electric Power Company, Wuhan 430062, China
Abstract: Building an equivalent model of mid-small sized hydropower generator group is a practical method carried out for dynamic analysis of water electricity grid; excitation and governor system have prominent influences on the precision of the equivalent model. This paper presents a method to build a dynamic equivalent model of hydropower generator units containing excitation and governing system. The method uses traditional equivalent model of hydropower generator group which is based on homology method as the foundation, and considers the equivalence of excitation and governor system; it uses PLPF method to get the equivalent parameters of excitation system and weighted average method to get the equivalent parameters of prime mover and speed governor. Numerical examples show that the error of the method in dynamic process is small; and it can improve the simulation accuracy. On this basis, further simulations are made to analyze the effect of excitation and governor system on dynamic characteristics.
Key words: hydropower generator group     dynamic equivalence     excitation system     PLPF method     governor    

随着我国中小型水电机群的逐步发展，水电能源接入电网的规模日益扩大.众多小水电站集中在水资源丰富的区域构成水电机群，总装机容量可达上千MW，如此大规模的中小水电并网发电时对主电网动态特性的影响不容忽视.与此同时，电网公司对提升电网运行分析能力提出了更高要求，因此，在对电网进行安全稳定分析时将中小型水电机群纳入考虑是非常必要的.

在对大型互联电网进行分析时，往往保留感兴趣的某一局部系统(也称为研究系统)而对外部子系统作适当的等值简化处理，在保证工程分析精度的同时减少计算量[1].该方法同样适用于中小水电机群接入主电网后的动态影响分析.

目前，针对电力系统的动态等值方法研究[1-7]已经较为成熟，但涉及水电领域的成果[8-10]并不多.文献[8-10]在建立水电机组等值模型时强调发电机本体的等值，对励磁和调速器系统的等值则采取近似简化或忽略不计的方式，然而研究表明[11]，励磁和调速器系统对电网动态仿真计算有较大影响.本文结合中小水电实际情况，对传统的水电机群等值模型进行改进，考虑励磁和调速器系统的等值，并分析励磁和调速系统对等值模型的动态影响.仿真结果表明计及励磁和调速系统的等值模型较传统模型具有更高的动态等值精度.

1 动态等值建模方法 1.1 等值建模步骤

采用基于同调法的中小水电机群等值模型，其建模过程可分为以下几个步骤：

1) 根据实际需要将整个系统分为研究系统与外部系统，对外部系统进行等值；

2) 根据电气距离判别同调机群，将隶属于同一同调群的若干发电机等值为1台等值机；

3) 将同调发电机母线合并为等值母线，同调机群内的负荷值等效移置至相应的等值母线上；

4) 对同调发电机本体、励磁系统、原动机及其调速器系统进行聚合得到等值机参数；

5) 采用REI法剩余网络进行化简；

6) 在等值系统的边界母线上引入虚拟负荷，平衡等值前后的系统潮流.

1.2 发电机本体和负荷模型

发电机采用4阶模型，模型方程:

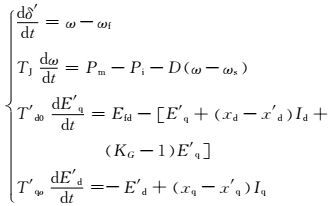    (1)

负荷为静态负荷，模型方程:

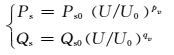    (2)
1.3 励磁系统的等值 1.3.1 励磁系统模型

目前中小型水电站优先采用自并励励磁系统[12]，PSASP中自并励系统传递函数框图如图 1所示.

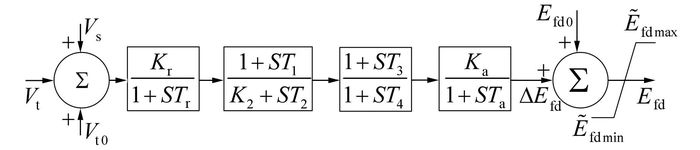
图 1 自并励励磁调节器框图 Figure 1 Block diagram of bus fed static excitation system
图选项
1.3.2 PLPF法

同调机群中各水电机组的励磁系统可能是多种多样的，往往无法直接使用加权平均法，而PLPF法[13]则具有可对不同类型的励磁系统聚合、精度较高、直接从时域采集信号等优点[14].

假设待辨识系统的常微分方程形式：

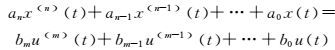    (3)

在零初始条件下，对式(3) 求n重积分，并引入积分运算矩阵H后，式(3) 的n重积分方程可改写为

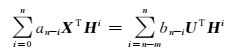    (4)

令an=1，利用加权最小二乘法可得到剩余的参数向量Θ，即

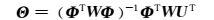    (5)

式中:W为权矩阵.

1.4 水轮机及其调速器的等值 1.4.1 水轮机模型

在电力系统稳定分析中，经常使用水轮机模型，如图 2所示.

图 2 水轮机模型 Figure 2 Ideal hydraulic turbine model
图选项

图 2中, μ为水轮机导水叶开度，Tw为水流时间常数，PM为输出机械功率.

1.4.2 水轮机调速器模型

目前国内所投运的水轮机调速器基本为“微机调节器+机械(电气)液压系统”的微机调速器[15]，虽然机械液压式和电气液压式2种类型的调速系统实现方法不同，但作用原理相似，因而可以采用相同的数学模型.其传递函数模型如图 3所示.

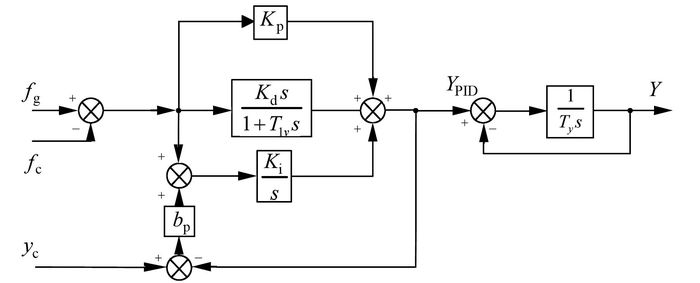
图 3 水轮机调速系统 Figure 3 Hydraulic turbine speed governor diagram
图选项
1.4.3 加权平均法

由于目前针对原动机及其调速系统尚没有成熟且精度高的等值方法，本文采用加权平均法[16]对同调发电机的水轮机及其调速系统进行聚合.

等值发电机的容量为等值区域内各台发电机的容量之和，即

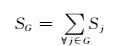    (6)

则水轮机及其调速系统的各参数:

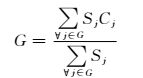    (7)

式中：CG为等值机水轮机及其调速系统的参数，包括水流时间常数Tw，PID环节参数KP、KI.

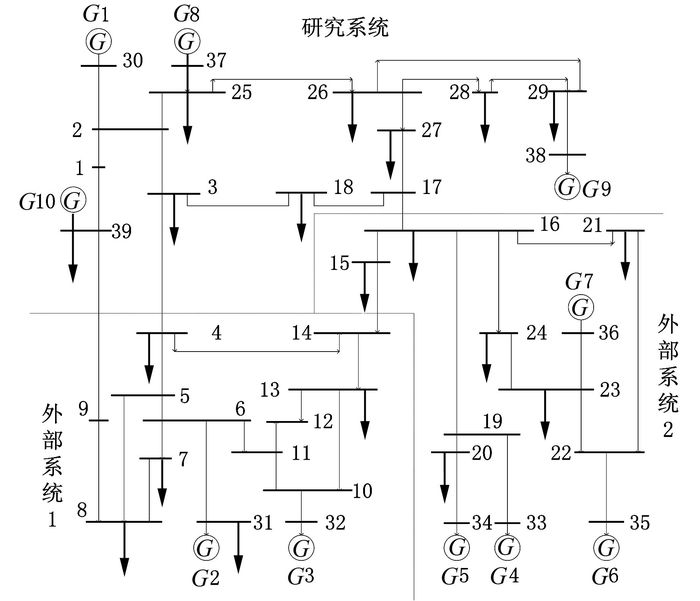
2 算例分析 2.1 算例1

算例1为改进的IEEE10机39节点系统，同调分群结果如图 4所示，其中外部系统1中有{G2，G3}共2台水轮机，外部系统2中有{G4、G5、G6、G7}共4台水轮机.故障方式是交流线3~18上50%处0.5 s发生3相短路故障，0.6 s故障消失.

图 4 IEEE10机39节点系统 Figure 4 IEEE 39 notes system with 10 generators
图选项

等值方案设置如表 1所示.

表 1 动态等值方案 Table 1 Dynamic equivalence scheme
方案号描述
1不考虑励磁系统与原动机调速系统等值
2考虑励磁系统但不考虑原动机调速系统等值
3同时考虑励磁系统与原动机调速系统等值
表选项

通过PSASP进行全系统仿真计算，可以得到原系统的稳态潮流值、联络线上有功及无功的变化量以及研究区域内发电机的功角响应曲线.再用等值系统计算相同故障方式下的动态响应，从而分析不同方案下模型的有效性，等值机励磁系统与原动机调速系统参数列于表 2，等值结果如表 3、4、图 5~7所示.

表 2 励磁系统与水轮机及其调速系统参数聚合结果 Table 2 Polymerization parameters of excitation system and hydraulic turbine with its speed governor
参数聚合值
Kr11.15
Tr10.035
Ka150.5
Ta10.025
Kp14.71
Ki11.04
Kd10.011
Tw11.1
Kr21.17
Tr20.033
Ka250.6
Ta20.028
Kp24.88
Ki21.01
Kd20.01
Tw21.12
表选项
表 3 研究系统内部分母线稳态电压值 Table 3 Steady voltage of part of study area bus
母线名电压/p.u.
原系统方案1方案2方案3
21.0511.0561.0561.056
261.0541.0581.0581.058
291.0511.0531.0531.053
表选项
表 4 稳态时区域间传输功率 Table 4 Steady transmission power between areap.u.
联络线编号
3-49-3916-17
原系统P
Q		1.08
1.45		0.32
-0.8		0.96
-0.4
方案1P
Q		1.12
1.31		0.30
-0.8		0.9
-0.4
方案2P
Q		1.12
1.35		0.31
-0.8		0.92
-0.4
方案3P
Q		1.12
1.35		0.31
-0.8		0.92
-0.4
表选项
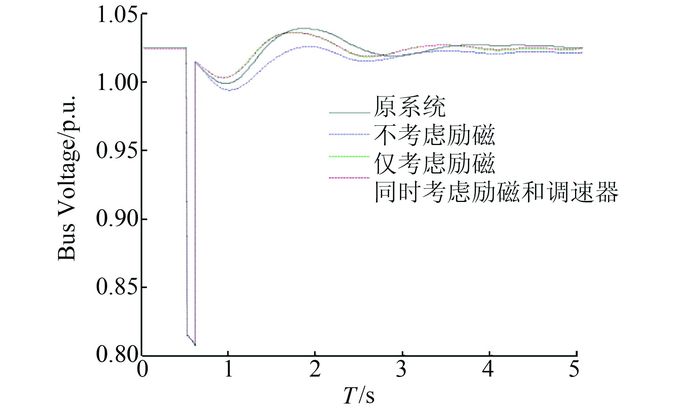
图 5 9号母线电压动态响应曲线 Figure 5 Dynamic voltage response curve of bus No.9
图选项
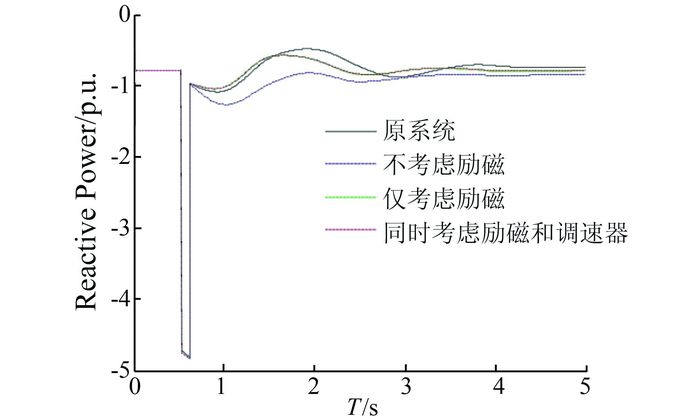
图 6 联络线功率动态响应曲线 Figure 6 Dynamic response curve of transmission line
图选项
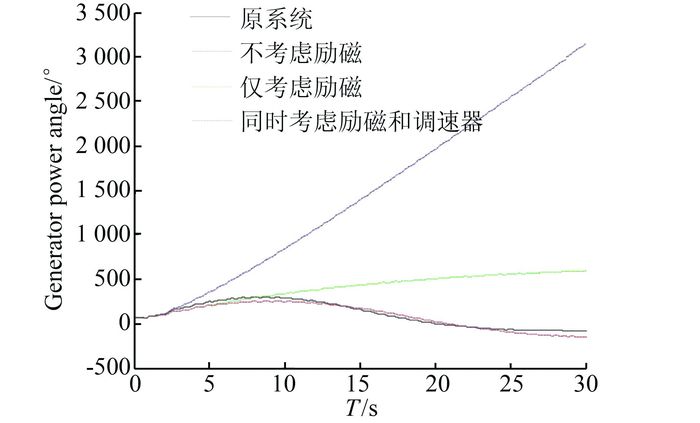
图 7 37号母线上发电机的功角动态曲线 Figure 7 Dynamic angle curve of generator on bus No.37
图选项

由表中数据可以看出，等值模型是否计及励磁系统和原动机及其调速器系统，其稳态潮流结果相差不大，且与原系统稳态潮流的误差均在允许范围内.

由图 5~7中曲线可以看出，考虑励磁系统的等值后，等值系统的电压、功率及功角的动态响应更接近于原系统，而原动机及其调速器对等值系统的电压、功率动态特性几乎没有影响，但对发电机功角特性影响较大，考虑原动机及其调速器的等值系统发电机功角摇摆曲线更接近于原系统.

对原系统和不同等值方案的等值系统分别进行小扰动分析计算，其结果如表 5、6所示.

表 5 部分振荡模式的频率 Table 5 Part of frequency of oscillation modes
模式频率/Hz
原系统方案1方案2方案3
11.244 51.246 11.246 11.246 1
21.006 61.007 21.007 01.006 9
30.811 20.813 20.811 70.811 7
40.513 00.531 00.528 30.5282
表选项
表 6 部分振荡模式的阻尼比 Table 6 Part of damping ratio of oscillation modes
模式阻尼比/%
原系统方案1方案2方案3
10.226 30.205 80.212 70.212 8
21.452 71.409 91.463 51.463 5
311.995 911.253 411.989 511.989 6
430.226 328.194 729.610 629.6106
表选项

由表 5、6可以看出，考虑励磁系统的等值模型振荡频率和阻尼比更接近于原系统，且仿真结果显示原系统研究系统内部及区域间振荡模式有8种，不考虑励磁系统的等值模型振荡模式有6种，考虑励磁系统的等值模型的振荡模式有8种，由以上分析得出，考虑励磁系统的等值模型小扰动特性更接近原系统.而原动机及其调速器则对等值模型的小扰动特性影响不大.

2.2 算例2

算例2为含恩施中小水电机群的湖北实际电网.恩施境内含中小水电站28座，机组89台，总装机容量1 330 MW，这些水电站经220 kV电压等级网接入恩施220 kV后通过500 kV恩渔线与湖北主网相连.对恩施水电机群等值后的系统如图 8所示.

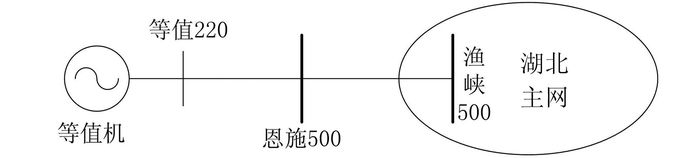
图 8 等值区域结构示意图 Figure 8 Equivalent structure diagram of Enshi
图选项

方案设置仍如表 1所示，暂态过程对比如图 9~11所示.

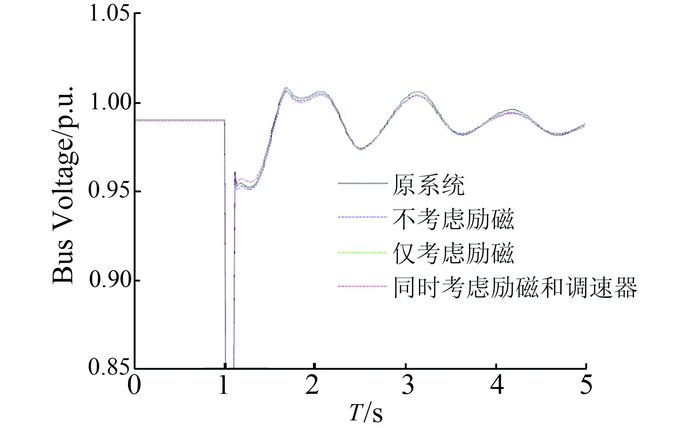
图 9 渔峡500 kV母线电压动态曲线 Figure 9 Dynamic voltage response curve of Yuxia 500 kV bus
图选项
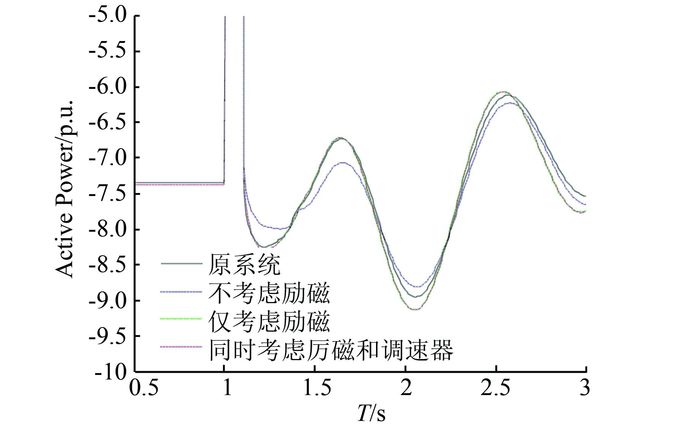
图 10 恩施500—渔峡500联络线功率动态曲线 Figure 10 Dynamic power response curve of transmission line between Enshi 500 kV and Yuxia 500 kV
图选项
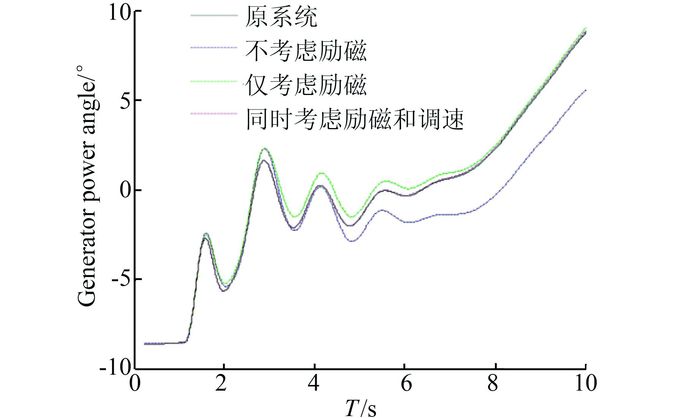
图 11 荆门热电厂发电机的功角动态曲线 Figure 11 Dynamic angle curve of Jingmen power plant
图选项

由于水电机群对整个大系统的动态影响并不显著，因此，在图 9中，即便不考虑励磁和调速器系统的等值，等值后的系统母线电压已经十分趋近于原系统.从图 10中可以看出，考虑励磁系统的等值模型，系统功率波动曲线较未考虑励磁更趋近于原系统.图 11则可看出，考虑励磁系统和考虑原动机都能提高等值模型中发电机功角的精度.

对原系统和等值系统分别进行小扰动分析，得到等值前后湖北电网存在的低频振荡模式，其结果如表 7、8所示.

表 7 部分振荡模式的频率 Table 7 Part of frequencies of oscillation modes
模式频率/Hz
原系统方案1方案2方案3
10.758 50.755 60.757 90.757 9
20.727 90.734 60.726 90.726 9
30.943 90.912 50.947 70.947 7
40.947 20.936 70.947 00.9470
表选项
表 8 部分振荡模式的阻尼比 Table 8 Part of damping ratios of oscillation modes
模式阻尼比/%
原系统方案1方案2方案3
117.599 217.4317.587 317.587 3
211.852 812.269 611.906 811.906 8
37.401 97.990 97.375 67.375 6
46.539 86.614 26, 534 16, 534 1
表选项

由表 7、8可以看出，考虑励磁系统后，等值系统的小扰动特性与原系统更相似.

3 结论

基于电网对动态分析精度不断提高的实际情况，并考虑到水电机组励磁和调速器系统对电网动态过程影响显著，本文建立了基于同调法的含励磁系统和原动机及其调速系统的中小水电机群等值模型.算例结果表明了模型的有效性，进一步分析得出，励磁系统对等值模型的暂态过程和小扰动特性影响显著，原动机及其调速器系统对等值模型中发电机的功角特性影响显著.本文方法为进一步提高中小水电机群等值模型精度提供了借鉴意义.

参考文献
[1] 周海强, 鞠平, 杨辉, 等. 电力系统动态等值建模研究述评[J]. 江苏电机工程, 2008, 29(5): 10–13.
Zhou Haiqiang, Ju Ping, Yang Hui, et al. Review of the research on dynamic equivalent modeling of power system[J]. Jiangsu Electrical Engineering, 2008, 29(5): 10–13.
[2] 鞠平, 韩敬东, 倪腊琴, 等. 电力系统动态等值的在线测辩研究(Ⅰ)—模型及其可辨识性[J]. 电力系统自动化, 1999, 23(4): 15–17.
Ju Ping, Han Jingdong, Ni Laqin, et al. Research on online measurement for dynamic equivalence of power system(Ⅰ)—model and identifiability[J]. Automation of Electric Power Systems, 1999, 23(4): 15–17.
[3] M Larbi Ourari, Louis-A Dessaint, Van Que Do. Dynamic equivalent modeling of large power systems using structure preservation technique[J]. IEEE Transactions on Power System, 2006, 21(3): 1284–1295. DOI:10.1109/TPWRS.2006.876699
[4] 许剑冰, 薛禹胜, 张启平, 等. 电力系统同调动态等值的述评[J]. 电力系统自动化, 2005, 29(14): 91–95.
Xu Jianbing, Xue Yusheng, Zhang Qiping, et al. Homology dynamic equivalence of power system[J]. Automation of Electric Power Systems, 2005, 29(14): 91–95. DOI:10.3321/j.issn:1000-1026.2005.14.019
[5] 鞠平. 电力系统建模理论与方法[M]. 北京: 科学出版社, 2010.
Ju Ping. Theory and Method of Power System Modeling[M]. Beijing: Science Press, 2010.
[6] 李晓辉, 罗敏, 刘丽霞, 等. 动态等值新方法及其在天津电网中的应用[J]. 电力系统保护与控制, 2010, 38(3): 61–66.
Li Xiaohui, Luo Min, Liu Lixia, et al. A new dynamic equivalence method and its application in Tianjin Grid[J]. Power System Protection and Control, 2010, 38(3): 61–66. DOI:10.7667/j.issn.1674-3415.2010.03.014
[7] 査晓明, 张扬, 成燕, 等. 用于简化微电网结构的微分几何广义同调方法[J]. 电工技术学报, 2012, 27(1): 24–31.
Zha Xiaoming, Zhang Yang, Cheng Yan, et al. New method of extended coherency for micro-grid based on homology in differential geometry[J]. Transactions of China Electrotechnical Society, 2012, 27(1): 24–31.
[8] 王敏, 文劲宇, 胡文博, 等. 区域小水电机群动态等值建模方法研究[J]. 电力系统保护与控制, 2013, 41(17): 1–9.
Wang Min, Wen Jinyu, Hu Wenbo, et al. A dynamic equivalent modeling for regional small hydropower generator group[J]. Power System Protection and Control, 2013, 41(17): 1–9. DOI:10.7667/j.issn.1674-3415.2013.17.001
[9] 白耀鹏. 小水电接入电网对系统运行影响的研究[D]. 北京: 北京交通大学, 2010.
Bai Yaopeng. Study on the impact of system operation grid-accessed small hydropower station[D]. Beijing: Beijing Jiaotong University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10004-2010120990.htm
[10] 张元胜. 分布式小水电对电力系统运行稳定性影响的研究[D]. 长沙: 湖南大学, 2012.
Zhang Yuansheng. The effects on stable running of power grid of the distributed network with small hydropower[D]. Changsha: Hunan University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10532-1012480960.htm
[11] 武诚, 徐政, 倪秋龙, 等. 基于响应特性的原动机及调速器建模与参数辨识[J]. 电工技术学报, 2012, 27(6): 226–231.
Wu Cheng, Xu Zheng, Ni Qiulong, et al. Modeling and parameter identification of turbine-governor based on response characteristics[J]. Transactions of China Electrotechnical Society, 2012, 27(6): 226–231.
[12] 戴宗泉. 小型水电站励磁系统对水轮机组运行的影响分析[J]. 中国水能及电气化, 2012(7): 29–32.
Dai Zongquan. Influence analysis of excitation system on hydraulic turbine set operation of small hydropower station[J]. China Water Power & Electrification, 2012(7): 29–32.
[13] 曹浩军, 张承学, 单勇. 基于连续时间方法的励磁系统参数辨识[J]. 电力系统自动化, 2004, 28(17): 49–54.
Cao Haojun, Zhang Chengxue, Shan Yong. Identification of excitation system parameter based on continuous-time method[J]. Automation of Electric Power Systems, 2004, 28(17): 49–54. DOI:10.3321/j.issn:1000-1026.2004.17.010
[14] 闻丹银, 孙黎霞, 黄桦, 等. 电力系统动态等值中励磁系统参数聚合方法对比研究[J]. 河海大学学报(自然科学版), 2012, 40(3): 350–356.
Wen Danying, Sun Lixia, Huang Hua, et al. Comparative studies on methods for parameter aggregation of excitation system for power system dynamic equivalent[J]. Journal of Hohai University(Natural Sciences), 2012, 40(3): 350–356.
[15] 李华, 史可琴, 范越, 等. 电力系统稳定计算用水轮机调速器模型结构分析[J]. 电网技术, 2007, 31(5): 25–33.
Li Hua, Shi Keqing, Fan Yue, et al. Structure analysis of water turbine governor model for stability calculation of power system[J]. Power System Technology, 2007, 31(5): 25–33.
[16] 胡杰, 余贻鑫. 电力系统动态等值参数聚合的实用方法[J]. 电网技术, 2006, 30(24): 26–30.
Hu Jie, Yu Yixin. A practical method of parameter aggregation for power system dynamic equivalence[J]. Power System Technology, 2006, 30(24): 26–30. DOI:10.3321/j.issn:1000-3673.2006.24.006