文章信息
- 李聪, 余正红, 周凤丽, 徐方
- LI Cong, YU Zhenghong, ZHOU Fengli, XU Fang
- 一种新的二进制编码量子行为粒子群优化算法
- A novel binary encoding quantum-behaved particle swarm optimization algorithm
- 武汉大学学报(工学版), 2017, 50(5): 784-789
- Engineering Journal of Wuhan University, 2017, 50(5): 784-789
- http://dx.doi.org/10.14188/j.1671-8844.2017-05-024
-
文章历史
- 收稿日期: 2016-10-27
2. 武汉大学计算机学院,湖北 武汉 430072
2. School of Computer, Wuhan University, Wuhan 430072, China
粒子群优化(Particle Swarm Optimization,PSO)是由Eberhart和Kennedy博士于1955年提出的一种基于群智能方法的演化计算技术[1, 2].孙俊对粒子群优化算法进行了深入研究,从量子力学的角度出发,提出了量子行为粒子群优化算法(QPSO)[3-5],QPSO参数更少且不包含粒子的速度,相比PSO其全局搜索能力更强[6].Kennedy于1997年提出了二进制PSO算法(BPSO)[7],2007年孙俊提出了二进制QPSO算法(BQPSO)[8].
本文在二进制QPSO算法中引入全面学习和合作方法,提出了一种新的二进制量子行为粒子群优化算法(CCBQPSO).完全学习策略可以保持群体的多样性,合作方法可以直接将算法引入到本地搜索,并快速收敛到最优解.在该算法中,所有粒子的个体最优位置可以首先参与到本地吸引子的更新,每个粒子的新解向量维度将依次取代对应粒子的先前个体最优位置和群体的全局最优位置的维度,并计算出适应值.
1 二进制粒子群优化算法(BPSO)PSO算法中,假设D维空间中的粒子群体规模为M,称为群集X.粒子i的第t代的位置矢量为xi(t)=(xi1(t), xi2(t), …, xiD(t)),速度矢量为vi(t)=(vi1(t), vi2(t), …, viD(t)),粒子的速度和位置更新公式分别为
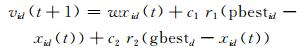 (1)
(1)
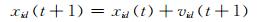 (2)
(2)
其中:i=1, 2, …, M;d=1, 2, …, D;w是惯性权重;c1和c2是学习因子;r1和r2是均匀分布在(0,1)区间内的随机数.粒子i的个体最优位置pbesti=(pbesti1, pbesti2, …, pbestiD),全局最优位置即种群中所有粒子的最优位置gbesti=(gbest1, gbest2, …, gbestD).
BPSO算法中,粒子的位置更新公式替换为
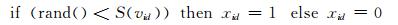 (3)
(3)
其中:S(v)是一个sigmoid函数,S(v)=1/(1+e-v);rand()是一个从区间(0,1)的均匀分布中随机产生的一个随机数.
2 二进制量子行为粒子群优化算法(BQPSO)量子行为粒子群优化算法(QPSO)中的相关公式如下:
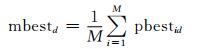 (4)
(4)
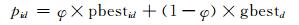 (5)
(5)
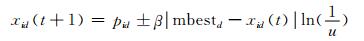 (6)
(6)
其中:φ是一个随机数;mbest表示群体的最优位置;参数β也被称为收缩-膨胀因子,可通过调节该参数对算法的收敛速度进行控制.
BQPSO算法中的粒子位置用二进制字符串表示,海明距离被定义为2个二进制字符串之间的不同比特位的计数值,即:
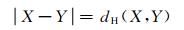 (7)
(7)
函数dH可获得二进制字符串X和Y之间的海明距离.
mbest的第j位取决于所有粒子的个体最优位置pbest中的第j位的状态,如果较多的粒子在各自pbest的第j位呈现为1,则mbest的第j位也为1,否则为0;若有一半的粒子在其pbest的第j位呈现为1,则mbest的第j位将随机设置为1或0,每种状态的概率为0.5.对pbesti和gbest作单点或多点交叉操作可得到点pi,具体过程为:先由交叉操作产生两个后代,然后随机选择其中一个后代并将其作为点pi输出.
考虑使用迭代公式(6)并将其转换为
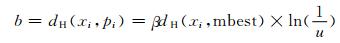 (8)
(8)
通过下式计算可得到一个概率,pi的每一个二进制位由此概率进行变异,再经过转过就可得到新的字符串xi:
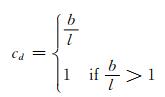 (9)
(9)
其中l表示粒子i的第d维的长度.在迭代过程中,如果rand() < cd,粒子i的位置中的对应位将反转,否则保持不变.
通过上述定义及对迭代公式的修改,BQPSO算法的步骤可描述如下:
步骤1 初始化所有粒子的二进制位的集合、pbest和gbest.
步骤2 确定每一个粒子的pbest和pi.
步骤3 计算每一维的变异概率cd并更新相应粒子的新位置xi.
步骤4 评估粒子的目标函数值,并将其与pbest和gbest的目标函数值进行比较,如果当前的目标函数值更好,则更新pbest和gbest.
步骤5 重复步骤2~4,直到满足算法的停止准则或已达到给定的最大迭代.
3 改进的二进制量子行为粒子群优化算法(CCBQPSO) 3.1 完全学习(Comprehensive Learning)在BQPSO算法中引入完全学习策略后,可以从任意粒子个体最优位置的相应维中随机挑选出本地吸引子pi的每一维的值[9],并对每个粒子i引入学习概率Ci,从而决定采用其中的哪一个粒子.对每个粒子i的每一维,如果rand()>Ci,pi将取自当前粒子本身的个体最优位置,否则将使用竞争选择策略去借鉴其他粒子的个体最优位置.
3.2 合作方式(Cooperative Approach)对于BQPSO算法中的目标函数f(X)=f[(X1,X2,…,XN)],全D维解向量将执行每个更新步骤,只要当前的目标函数值优于之前得到的值,更新pbest和gbest,这样解向量中的某些维度会逐渐靠近全局最优,而另外一些则将逐步远离全局最优;如果解向量中的目标函数劣于之前得到的值,当前解向量将在算法的下次迭代中弃用,同时该解向量附带的有价值信息也将丢失.为了避免上述行为,可将合作方法引入至算法中[10],新的解向量的每一维反过来取代pbest和gbest的对应维,并与新的目标函数值进行比较,从而决定是否更新pbest和gbest.算法过程描述如下:
步骤1 对每个粒子i,初始化cgbest=gbest,cpbesti=pbesti.
步骤2 用粒子i的对应维替换cpbest和cgbest的维.
步骤3 评估cpbest和cgbest的当前目标函数值,将其与pbest和gbest的目标函数值进行比较.如果当前值优于pbest和gbest,则更新pbest和gbest.
步骤4 重复2~3步,直到粒子的所有维都被比较过.
3.3 CCBQPSO综上所述,一种基于全面学习和合作方式的新的二进制量子粒子群优化算法(CCBQPSO)被提出,算法描述如下:
步骤1 初始化.
步骤2 利用全面学习策略将每个粒子更新至本地吸引子pi.
步骤3 使用BQPSO算法更新粒子的新位置xi.
步骤4 评估粒子的目标函数值,并将其与pbest和gbest的目标函数值进行比较,如果当前的目标函数值更好,则更新pbest和gbest.
步骤5 使用合作方式更新pbest和gbest.
步骤6 重复步骤2~5,直到满足算法的停止准则或已达到给定的最大迭代.
该算法通过比较解向量的每一维来提高收敛精度,必须扩大搜索空间并增加时间消耗,为此又提出了2个自适应控制方法:
1) 一旦新的目标函数值比之前的更差,执行合作策略.
2) 一旦粒子二进制位不同于pbest和gbest的对应二进制位,执行合作策略.
4 实验与分析在CCBQPSO算法的性能测试中选用了如表 1所示的5个不同标准函数[7],并将结果与标准的BPSO、BQPSO和CLBQPSO算法进行了比较.
| 测试函数 | 范围 |
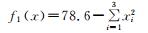 |
xi∈[-5.12, 5.12] |
| f2(x)=3905.93-(100×(x12-x2)2-(1-x1)2) | xi∈[-2.048, 2.048] |
| f3(x)=25-(x1+x2+x3+x4+x5) | xi∈[-5.12, 5.12] |
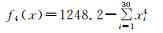 |
xi∈[-1.28, 1.28] |
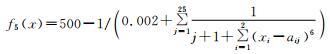 |
 |
所有算法的参数设置如下:BPSO算法中的学习因子c1=c2=2,惯性权重w的最大值为0.9,最小值为0.4;BQPSO、CLBQPSO及CCBQPSO算法中的参数β值为1.4[11];学习概率的所有参数Ci=0.5.在种群规模分别取20、40和80的条件下所有算法均独立运行50次,且在成功迭代200次后所有算法停止运行.对每个算法进行测试后可得到最好适应值(Best Fitness Value,BFV)、最大BFV、最小BFV、平均BFV以及获取最大BFV时算法迭代的次数,表 2~6显示了平均BFV、最小BFV以及在50次测试运行中可获取到最大BFV时的算法迭代次数.
| 种 群 规 模 |
BPSO | BQPSO | CLBQPSO | CCBQPSO | |||||||||||
| 平均BFV | 最小BFV | 算法搜寻次数 | 平均BFV | 最小BFV | 算法搜寻次数 | 平均BFV | 最小BFV | 算法搜寻次数 | 平均BFV | 最小BFV | 算法搜寻次数 | ||||
| 20 | 78.599 86 | 78.599 7 | 7 | 78.599 87 | 78.599 7 | 12 | 78.599 67 | 78.597 4 | 2 | 78.6 | 78.599 9 | 48 | |||
| 40 | 78.599 85 | 78.599 7 | 2 | 78.599 89 | 78.5997 | 13 | 78.599 86 | 78.599 5 | 9 | 78.6 | 78.600 0 | 50 | |||
| 80 | 78.599 84 | 78.599 7 | 4 | 78.599 92 | 78.599 7 | 20 | 78.599 92 | 78.599 7 | 18 | 78.6 | 78.600 0 | 50 | |||
| 种 群 规 模 |
BPSO | BQPSO | CLBQPSO | CCBQPSO | |||||||||||
| 平均BFV | 最小BFV | 算法搜寻次数 | 平均BFV | 最小BFV | 算法搜寻次数 | 平均BFV | 最小BFV | 算法搜寻次数 | 平均BFV | 最小BFV | 算法搜寻次数 | ||||
| 20 | 3 905.900 2 | 3 905.153 6 | 9 | 3 905.910 2 | 3 905.781 5 | 10 | 3 905.928 0 | 3 905.911 6 | 4 | 3 905.928 9 | 3 905.914 0 | 9 | |||
| 40 | 3 905.924 2 | 3 905.841 8 | 18 | 3 905.923 5 | 3 905.831 2 | 13 | 3 905.929 3 | 3 905.924 7 | 7 | 3 905.929 8 | 3 905.929 2 | 11 | |||
| 80 | 3 905.929 2 | 3 905.918 8 | 15 | 3 905.929 2 | 3 905.921 4 | 20 | 3 905.929 8 | 3 905.929 2 | 10 | 3 905.929 9 | 3 905.929 7 | 25 | |||
| 种 群 规 模 |
BPSO | BQPSO | CLBQPSO | CCBQPSO | |||||||||||
| 平均BFV | 最小BFV | 算法搜寻次数 | 平均BFV | 最小BFV | 算法搜寻次数 | 平均BFV | 最小BFV | 算法搜寻次数 | 平均BFV | 最小BFV | 算法搜寻次数 | ||||
| 20 | 54.86 | 54 | 43 | 54.96 | 54 | 48 | 54.66 | 54 | 33 | 54.96 | 54 | 48 | |||
| 40 | 54.98 | 54 | 49 | 55.00 | 55 | 50 | 54.78 | 54 | 40 | 54.98 | 54 | 49 | |||
| 80 | 55.00 | 55 | 50 | 55.00 | 55 | 50 | 54.94 | 55 | 47 | 55.00 | 55 | 50 | |||
| 种 群 规 模 |
BPSO | BQPSO | CLBQPSO | CCBQPSO | |||||||||||
| 平均BFV | 最大BFV | 最小BFV | 平均BFV | 最大BFV | 最小BFV | 平均BFV | 最大BFV | 最小BFV | 平均BFV | 最大BFV | 最小BFV | ||||
| 20 | 1 250 | 1 258 | 1 240 | 1 253 | 1 261 | 1 247 | 1 252 | 1 259 | 1 244 | 1 261 | 1 268 | 1 248 | |||
| 40 | 1 251 | 1 263 | 1 241 | 1 252 | 1 262 | 1 245 | 1 252 | 1 260 | 1 247 | 1 262 | 1 271 | 1 253 | |||
| 80 | 1 251 | 1 264 | 1 243 | 1 254 | 1 260 | 1 245 | 1 252 | 1 261 | 1 247 | 1 262 | 1 273 | 1 252 | |||
| 种 群 规 模 |
BPSO | BQPSO | CLBQPSO | CCBQPSO | |||||||||||
| 平均BFV | 最小BFV | 算法搜寻次数 | 平均BFV | 最小BFV | 算法搜寻次数 | 平均BFV | 最小BFV | 算法搜寻次数 | 平均BFV | 最小BFV | 算法搜寻次数 | ||||
| 20 | 498.711 63 | 497.763 06 | 9 | 498.752 78 | 497.819 77 | 11 | 499.255 60 | 498.796 5 | 22 | 499.241 35 | 499.057 11 | 31 | |||
| 40 | 498.959 86 | 498.108 09 | 13 | 498.972 92 | 497.622 03 | 7 | 499.257 85 | 499.113 0 | 33 | 499.261 06 | 499.000 00 | 38 | |||
| 80 | 499.038 57 | 498.109 06 | 19 | 498.949 43 | 498.108 09 | 23 | 499.269 89 | 499.269 8 | 46 | 499.269 90 | 499.269 75 | 48 | |||
从表 2可以看出,f1函数的最优适应值为78.6,且所有算法均可求出该值;CCPQPSO算法所求得的平均BFV优于其他3种算法;BQPSO算法优于BPSO和CLBQPSO算法;当种群规模为20时BPSO算法优于CLBQPSO算法,但是当种群规模为40和80时BPSO算法则劣于CLBQPSO算法;CLBQPSO算法所求得的最小BFV劣于其他算法.就求解质量而言,CCBQPSO算法的成功搜寻次数是最多的,BQPSO算法次之;当种群规模为20时CLBQPSO算法搜寻2次后得到最优值,而BPSO算法则需要搜寻7次,当种群规模为40时相应搜寻次数变为9和2,当种群规模增大至80时,CLBQPSO和BPSO算法在寻找最优值的过程中分别需要搜索18和4次.
从表 3可以看出,f2函数的最优适应值为3 905.93,且所有算法均可求出该值;CCBQPSO算法所求得的平均BFV最优,其次是CLBQPSO算法;当种群规模为40时BQPSO算法的性能劣于其他3种算法;需要注意到CLBQPSO算法的成功搜寻次数明显劣于其他算法,但是当种群规模为20时其他3种算法的成功搜寻次数基本相同,当种群规模为40时BPSO算法性能最优,当种群规模为80时相比较BQPSO算法的成功搜索次数而言,CCBQPSO算法明显更胜一筹.
从表 4可以看出,f3函数的最优适应值为55,且所有算法均可求出该值;BQPSO算法所求得的平均BFV最优;当种群规模为80时,CCBQPSO、BQPSO及BPSO算法均搜索了50次才得到最优值;当种群规模为20和40时,CCBQPSO算法优于BPSO及CLBQPSO算法.
为了测试整个种群的平均适应值,f4函数中引入了高斯噪声.从表 5可以看出,CCBQPSO算法得到的平均BFV最大,CLBQPSO算法求得的平均BFV劣于BQPSO算法但是却优于BPSO算法;当种群规模为80时,CLBQPSO算法得到的最大BFV和最小BFV优于BQPSO算法;当种群规模为40时,CLBQPSO算法得到的最小BFV也优于BQPSO算法.
从表 6可以看出,f5函数的最优适应值为500,所有算法得到的最优值为499.26991;CCBQPSO算法得到的平均BFV和成功搜寻次数最优,CLBQPSO算法次之.
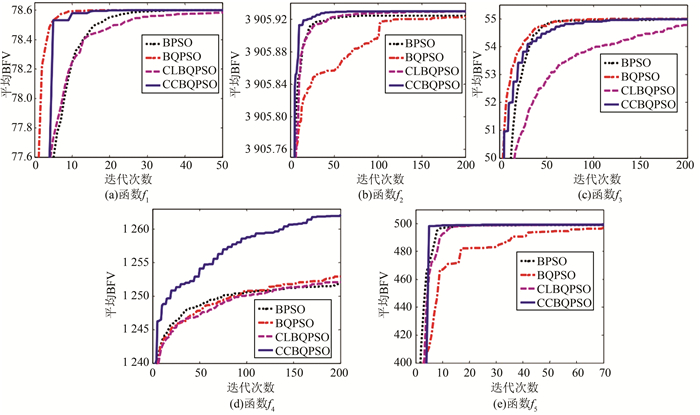
当4种算法的种群规模为40且运行次数超过50时,利用5个测试函数所得到的平均BFV的收敛曲线如图 1所示.当测试函数为f1时,早期BQPSO算法的收敛速度较快,但很快CCBQPSO算法就超越了BQPSO算法并生成了一个较好的解决方案;当测试函数为f2时,CCBQPSO算法相对于其他3种标准算法而言收敛速度更快,所得到的解决方案也最优;当测试函数为f3时所得到的平均BFV收敛曲线与测试函数为f1时的曲线较为相似,虽然BQPSO算法的收敛速度在初期是最快的,最终CCBQPSO算法还是超越BQPSO算法并生成了一个较好的解决方案;当测试函数为f4时,CCBQPSO算法的收敛速度和得到的解决方案一直优于其他3种标准算法;当测试函数为f5时,虽然初期其他3种算法的收敛速度均快于CCBQPSO算法,最终CCBQPSO算法的寻优能力明显高于它们.
|
| 图 1 种群规模为40时4种算法的收敛曲线 Figure 1 Four kinds of convergence curves when population size is 40 |
综上所述,实验结果表明了所提出CCBQPSO算法的有效性,全面学习可以保持群体的多样性并能更好地进行全局搜索,而合作方式直接将算法引入到本地搜索,提高了算法的收敛速度和寻优能力.
5 结论本文提出了一种新的二进制量子粒子群优化算法(CCBQPSO).在该算法中,所有粒子的个体最优位置用于本地吸引子的更新,避免粒子收敛到局部最优,且粒子每一维的更新都会反馈至个体最优位置和全局最优位置.实验结果表明CCBQPSO算法的全局收敛能力优于其他算法,但是随着问题复杂度的增加,使用CCBQPSO算法将会浪费大量时间,下一步将会对这个缺陷进行改进.
| [1] | Kennedy J, Eberhart R. Particle swarm optimization[C]// Proceedings of IEEE International Conference on Neural Networks(ICNN 1995), IEEE Press, 1995: 1942-1948. |
| [2] | Van den Bergh F. An analysis of particle swarm optimizers[D]. University of Pretoria, South Africa, 2002. http://www.oalib.com/references/19346618 |
| [3] | Sun J, Feng B, Xu W B. Particle swarm optimization with particles having quantum behavior[C]// Proceedings of IEEE Congress on Evolutionary Computation(CEC 2004), IEEE Press, 2004: 325-331. |
| [4] | Sun J, Fang W, Wu X J, et al. Quantum-behaved particle swarm optimization: Analysis of individual particle behavior and parameter selection[J]. Evolutionary Computation, 2012, 20(12): 349–393. |
| [5] | Fang W, Sun J, Ding Y R, et al. A review of quantum-behaved particle swarm optimization[J]. IETE Technical Review, 2010, 27(7): 336–348. |
| [6] | Sun J, Wu X J, Palade V, et al. Convergence analysis and improvements of quantum-behaved particle swarm optimization[J]. Journal of Information Science, 2012, 193(6): 81–103. |
| [7] | Kennedy J, Eberhart R. A discrete binary version of the particles swarm algorithm[C]// Proceedings of IEEE International Conference on Systems, Man and Cybernetics, IEEE Press, 1997: 4104-4108. |
| [8] | Sun J, Xu W B, Fang W, Chai Z L. Quantum-behaved particle swarm optimization with binary encoding[C]// Proceedings of International Conference on Adaptive and Natural Computing Algorithms, Springer Berlin Heidelberg, 2007: 376-385. |
| [9] |
陈伟, 傅毅, 孙俊, 等. 一种改进二进制编码量子行为粒子群优化聚类算法[J].
决策与控制, 2011(10): 1463–1468.
Chen Wei, Fu Yi, Sun Jun, et al. Improved binary quantum-behaved particle swarm optimization clustering algorithm[J]. Control and Decision, 2011(10): 1463–1468. |
| [10] | Van den Bergh F, Engelbrecht A P. A cooperative approach to particle swarm optimization[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(6): 225–239. |
| [11] |
孙俊. 量子行为粒子群优化算法研究[D]. 无锡: 江南大学, 2009.
Sun Jun. Particle swarm optimization with particles having quantum behavior[D]. Wuxi: Southern Yangtze University, 2009. http://www.oalib.com/references/19488805 |
 2017, Vol. 50
2017, Vol. 50



