文章信息
- 桂俊平, 常湧, 李行之, 石林, 黄华
- GUI Junping, CHANG Yong, LI Xingzhi, SHI Lin, HUANG Hua
- 基于分时电价的电动汽车充电负荷影响研究
- Time-of-use price-based research on electric vehicle charging load influence
- 武汉大学学报(工学版), 2018, 51(10): 915-919, 935
- Engineering Journal of Wuhan University, 2018, 51(10): 915-919, 935
- http://dx.doi.org/10.14188/j.1671-8844.2018-10-011
-
文章历史
- 收稿日期: 2016-12-18
电动汽车以可再生的电能为燃料,减少了对化石燃料的依赖和温室气体的排放.近年来电动汽车的发展得到了人们的青睐[1],已成为各国政府、汽车制造商、相关企业关注的焦点[2].各国汽车公司都在大力研究电动汽车的相关技术,也取得了突破性的进展,电动汽车的发展前景不可估量,而且在未来会拥有巨大的市场[3-5].
大量的电动汽车充电负荷接入电网,将会对电网产生不小的影响.电动汽车用户众多,出行习惯各不相同,如果电动汽车用户采用用完即充的无序充电方式,可能在每天某一时段集中充电,导致电网负荷出现峰上加峰的现象,增加电网负担,造成电网负荷拥塞,降低电能质量.分时电价能够引导电动汽车有序充电,降低电动汽车充电对电网的不利影响, 达到削峰填谷的作用,提高电网经济稳定运行能力.但是分时电价也可能使电动汽车用户在低电价时段集中充电,引起负荷拥塞,对电网安全稳定造成不良影响[6-8].
文献[9]通过建立峰谷分时电价的数学模型对电动汽车用户进行引导,然后以削峰填谷的效果为目标函数对模型进行优化,得到峰谷电价下的最优模型.文献[10]根据电动汽车车主的充电习惯和充电站的负荷容量为约束条件,以峰谷差最小为目标,提出了站内控制的分时电价制定方法.文献[11]分析了电动汽车车主的用车需求,在此基础上建立了以峰谷差最小为目标的最优有序充电控制模型,并采用了在电动汽车充电随机性较大下的调度最优潮流模型.文献[12]提出了一种新的考虑分时电价的电动汽车充电负荷计算方法,这种方法对分时电价时段的制定以及对现行分时电价下的充电负荷对电网的影响评估有着重要意义.但上述文献均在分时电价控制策略下,电动汽车充电负荷对电网负荷削峰填谷的角度进行研究分析,忽视了分时电价下低价时段大量电动汽车充电负荷接入电网的负面影响.
本文以电动汽车中私家车用户的慢充电负荷为主要研究对象,利用蒙特卡洛法对电动汽车无序充电进行数学建模,仿真出电动汽车无序充电时的电网日负荷曲线.引入有序充电的概念,建立峰谷分时电价下的电动汽车有序充电模型,仿真得到不同用户响应系数下的电网日负荷曲线.对分时电价下不同用户相应系数时的电网日负荷曲线进行对比分析,得出相关结论.
1 电动汽车无序充电 1.1 电动汽车充电的影响因素电动汽车充电负荷的影响因素主要包括电动汽车的电池状态和电动汽车用户的出行习惯[13-14].
由于锂电池具有放电稳定、持续、储存电能容量大等优点,今后会成为电动汽车中广泛采用的电池.锂电池在进行充电时,充电负荷会受到几个因素的影响[15-16],包括电池的充电电流、荷电状态、健康状态以及充放电次数.不同型号容量的锂电池也会导致电动汽车的充电行为大不相同,因此需要对大规模电动汽车的充电行为进行简化.
电动汽车负荷预测的另一个主要影响因素是用户的出行习惯.电动汽车用户的出行在工作日和节假日会有明显的不同,在工作日时,电动汽车用户在上下班之后,将电动汽车的电量充满.在节假日时,电动汽车充电时间的分布会比较均匀.目前研究的充电对象有公交车、出租车、公务车和私家车,考虑到未来大部分的电动汽车会是私家车,而且私家车的充电受分时电价影响较大,因此本文研究的主要对象是电动汽车私家车用户工作日充电负荷.
为定量分析大规模电动汽车工作日充电负荷对电网负荷曲线的影响,对电动汽车的充电行为做如下简化:
(a) 电动汽车电池的容量C=25~35 kW·h;
(b) 电动汽车充电功率Pcd在3~5 kW内平均分布;
(c) 考虑到电动汽车电池的损耗和相关参数的逐渐改变,假设电动汽车充电电池的荷电状态为10%~90%;
(d) 本文考虑1 d中0点到24点充电负荷的分布情况,且每一辆电动汽车一天充电次数期望为1;
(e) 分时电价的峰时段电价较高,电动汽车私家车用户会尽量选择在谷电价时段充电.
1.2 电动汽车无序充电模型目前缺乏电动汽车出行的相关数据,在未实施电价引导政策的情况下,电动汽车私家车用户在工作日时,会在上午上班,到达公司后选择在公司充电,将电动汽车的电量补满,或是下午下班回家后会在家充电.私家车用户无序充电模型为20%的用户充电起始时间符合N(9,0.52),50%的用户充电起始时间符合N(19,1.52),还有30%的用户起始时间符合U(0,24).电动汽车无序充电起始充电时间的概率分布密度:
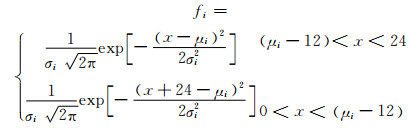 (1)
(1)
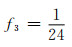 (2)
(2)
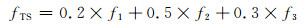 (3)
(3)
其中:i=1, 2;σ1=0.5;σ2=1.5;μ1=9;μ2=19.
设电动汽车在行驶结束后就开始充电,则汽车的行驶结束时间即电动汽车的起始充电时间,充电行为服从1.1节中做出的简化.
基于对私家车主的出行习惯的假设,可得到电池充电的持续时长TC的计算公式:
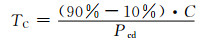 (4)
(4)
式中:C为随机抽取的电池容量,kW·h;Pcd为随机抽取的充电功率,kW;TC为电动汽车的充电持续时间,h.
2 蒙特卡洛模拟 2.1 蒙特卡洛法蒙特卡洛法是数学中的一种随机抽样或统计试验方法.采用蒙特卡洛法对一辆电动汽车的充电起始时间、电池充电电量以及充电的平均功率进行抽样,然后通过计算叠加,便可得到电动汽车的充电负荷曲线[16-18].
2.2 预测基本原理某地区在某一时刻的电动汽车充电负荷为该地区在这一时刻每辆电动汽车充电负荷相加.在Matlab中将1 d 24 h分为2 400份,每0.01 h为一个时刻,并对私家车负荷采用蒙特卡洛法进行抽样仿真,对电动汽车充电负荷进行叠加,得到充电的总负荷P,计算公式如下:
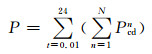 (5)
(5)
式中:N代表该地区1 d中充电的私家车数量;Pcdn代表在抽取t时刻的N辆电动汽车中某一辆车的充电功率.
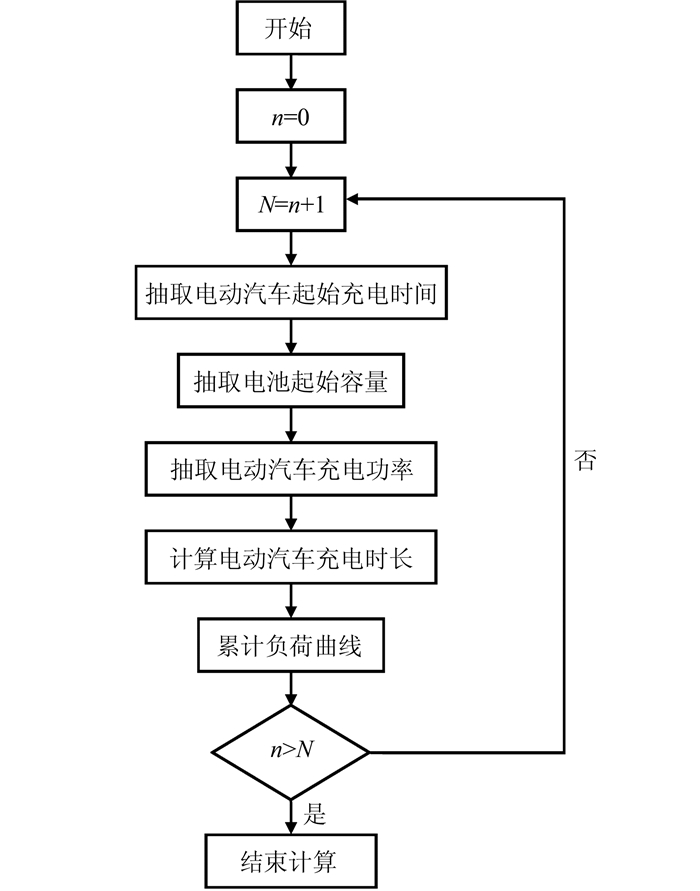
2.3 蒙特卡洛仿真由前述相关假设及原理,根据建立的电动汽车充电模型,采用蒙特卡洛法抽取电动汽车起始充电时间、充电功率,计算充电持续时间,对充电模型进行仿真,得到电动汽车充电负荷预测曲线,计算流程如图 1所示.
|
| 图 1 电动汽车充电负荷预测流程图 Fig. 1 Flowchart based on electric vehicle charging load forecast |
电动汽车有序充电是指采用合理有效的政策或技术手段对电动汽车充电进行引导和控制,使电动汽车负荷避开电网负荷高峰,分布在电网负荷低谷时期,达到削峰填谷的作用,改善电网负荷分布,提高电网经济稳定运行能力.现在的引导策略是分时电价策略,研究结果表明该策略对电动汽车负荷引导、对电网削峰填谷起到明显的作用.
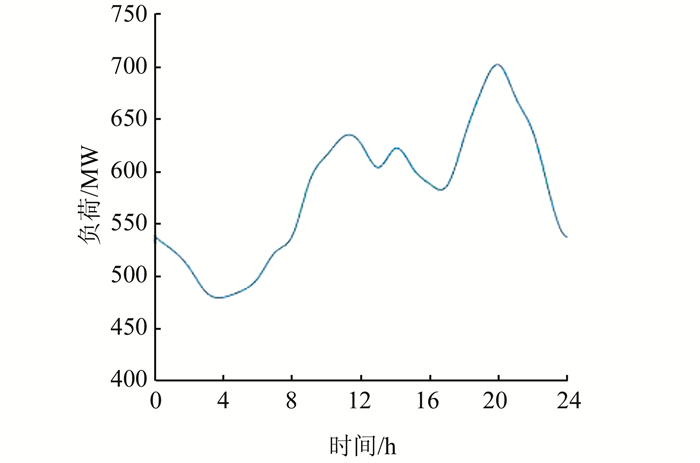
3.2 分时电价下有序充电模型某市的日负荷曲线如图 2所示.
|
| 图 2 某市的日负荷预测曲线 Fig. 2 A typical daily load curve in a city |
为了降低日负荷曲线的峰谷差率,使电动汽车充电负荷达到削峰填谷的效果,对该市的峰谷分时电价时段设定为:凌晨1:00-8:00为低谷电价,白天8:00-次日1:00为高峰电价.
电动汽车私家车用户为了使购电费用较低,选择响应分时电价控制策略,会在谷电价起始时刻附近开始充电.设置响应分时电价的私家车用户充电起始时间负荷大致服从N(1, 0.22)分布,没有响应分时电价的私家车用户仍然服从电动汽车无序充电模型.
3.3 用户响应系数η用户响应系数η是响应分时电价的电动汽车占总电动汽车的比例.例如1 d 24 h中一共有N辆电动汽车进行充电,其中η×N辆电动汽车充电的起始时间分布服从分时电价下的有序充电模型,(1-η)×N辆电动汽车充电起始时间分布服从工作日下的无序充电模型,本文对η=25%,50%,75% 3种情况进行计算仿真,分析比较电动汽车用户在低谷价时段大量接入对电网负荷的影响.
4 仿真算例采用蒙特卡洛方法对电动汽车无序充电情况进行日负荷预测,然后仿真分时电价下3种不同用户响应情况下的电动汽车充电日负荷曲线,并分别叠加到电网负荷曲线,形成该市1 d总负荷曲线,并对得到的曲线进行分析比较.
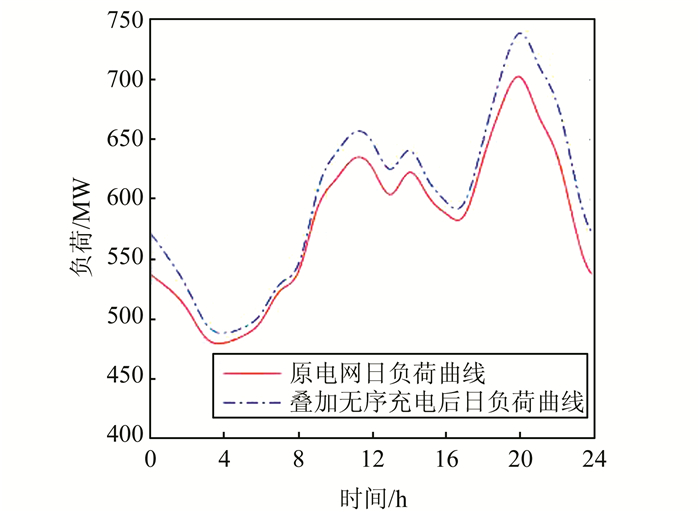
4.1 仿真结果预测该市2020年电动汽车数量将达到2万辆,根据该市电动汽车发展规模的预测,对2020年电动汽车中私家车在工作日时充电负荷进行模拟仿真,可得到2020年接入电动汽车负荷后该市的总负荷曲线,如图 3所示.
|
| 图 3 无序充电下电网日负荷曲线 Fig. 3 Power daily load curve of disorderly charging |
对曲线进行分析可以得到表 1所示的结果.
| 负荷情况 | 负荷/MW | 峰谷差率p | |
| 峰值 | 谷值 | ||
| 叠加之前 | 702.6 | 479.6 | 0.317 4 |
| 叠加无序 | 738.9 | 488.4 | 0.339 0 |
该市若采取分时电价控制策略,那么用户的充电习惯会发生改变,影响电网的日负荷分布情况.对2020年电动汽车中私家车工作日充电负荷采用蒙特卡洛法进行模拟仿真,代入用户响应系数η,将η=25%,50%,75% 3种情况下电动汽车负荷叠加到该市的日负荷曲线.
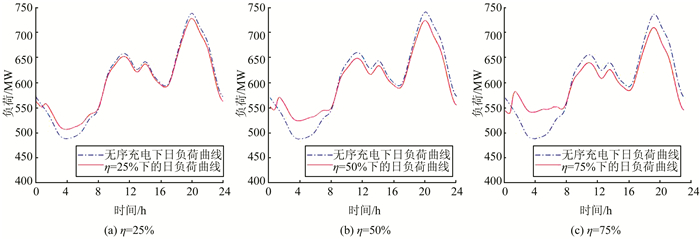
在分时电价不同用户相应系数下,接入电动汽车负荷后该市总负荷曲线如图 4所示.
|
| 图 4 电网日负荷曲线 Fig. 4 Power daily load curve |
对曲线进行分析可以得到表 2所示的结果.
| 负荷情况 | 峰谷差率p | 冲击峰值/MW | 冲击幅值/MW |
| 无序充电 | 0.339 0 | 0 | 0 |
| η=0.25 | 0.304 1 | 557.8 | 6.8 |
| η=0.50 | 0.272 6 | 570.4 | 25.2 |
| η=0.75 | 0.242 8 | 583.8 | 45.1 |
通过上述仿真,在叠加电动汽车无序充电负荷前后,以及分时电价策略引导用户有序充电下,在不同的用户响应系数下的电网日负荷曲线对比分析,可以得到以下结论:
1) 电动汽车用户进行无序充电时,增加电网负荷峰值,增大日负荷峰谷差率,给电网运行造成压力.因此,大规模电动汽车充电负荷接入电网时,需要对电动汽车充电行为进行引导和控制.
2) 在峰谷分时电价策略的引导下,电动汽车充电负荷对电网起到了明显的削峰填谷作用,有效地降低了电网负荷的峰谷差率,减小电网运行负担.随着分时电价下用户响应系数的逐步增加,削峰填谷的效果更加明显.
3) 采取分时电价策略时,电动汽车用户为了购电费用更少,会集中在谷电价起始时刻附近开始充电,大量的电动汽车短时间内接入电网,使电网的负荷激增,造成负荷堵塞,加重电力系统的负担.随着用户响应系数的增加,电动汽车冲击负荷的幅值逐步增大,对电网的影响也加大.
5 结语通过对仿真结果的对比分析,可以得出:在峰谷分时电价策略的引导下,电动汽车充电负荷对电网起到了削峰填谷的作用,有效地降低了电网负荷的峰谷差率;电动汽车用户短时间集中开始充电使电网的负荷激增,加重电力系统的负担;随着用户响应系数的增大,影响效果更加明显.本文的相关结论对电动汽车有序充电控制策略研究具有重要的参考意义.
| [1] |
Boulanger A G, Chu A C, Maxx S, et al. Vehicle electrification: status and issues[J]. Proceedings of the IEEE, 2011, 99(6): 1116-1138. DOI:10.1109/JPROC.2011.2112750 |
| [2] |
Saber A Y, Venayagamoorthy G K. Optimization of vehicle-to-grid scheduling in constrained parking lots[C]// Proceedings of IEEE Power & Engineering Society General Meeting, 2009: 1-8.
|
| [3] |
胡春泽, 宋永华, 徐智威, 等. 电动汽车接入电网的影响与利用[J]. 中国电机工程学报, 2012, 32(4): 1-10. Hu Zechun, Song Yonghua, Xu Zhiwei, et al. Impacts and utilization of electric vehicles integration into power systems[J]. Proceedings of the CSEE, 2012, 32(4): 1-10. |
| [4] |
苗轶群, 江全元, 曹一家. 考虑电动汽车及换电站的微网随机调度研究[J]. 电力自动化设备, 2012, 32(9): 18-24, 39. Miao Yiqun, Jiang Quanyuan, Cao Yijia. Microgrid stochastic dispatch considering electric vehicles and battery swap stations[J]. Electric Power Automation Equipment, 2012, 32(9): 18-24, 39. |
| [5] |
Shao Shengnan, Pipattanasomporn M, Rahman S.Challenges of PHEV penetration to the residential distribution network[C]// Proceedings of IEEE Power & Energy Society General Meeting, 2009: 1-8.
|
| [6] |
黄润.电动汽车入网对电网负荷影响的研究[D].上海: 上海交通大学, 2012: 14-18. Huang Run. Impacts of electric vehicles charging on the load of power system[D]. Shanghai: Shanghai Jiaotong University, 2012: 14-18. |
| [7] |
赵俊华, 文福拴, 杨爱民, 等. 电动汽车对电力系统的影响及其调度与控制问题[J]. 电力系统自动化, 2011, 35(14): 2-10. Zhao Junhua, Wen Fushuan, Yang Aimin, et al. Impacts of electric vehicles on power systems as well as the associated dispatching and control problem[J]. Automation of Electric Power Systems, 2011, 35(14): 2-10. |
| [8] |
孙晓明, 王玮, 苏粟, 等. 基于分时电价的电动汽车有序充电控制策略设计[J]. 电力系统自动化, 2013, 37(1): 191-195. Sun Xiaoming, Wang Wei, Su Li, et al. Coordinated charging strategy for electric vehicles based on time-of-use price[J]. Automation of Electric Power Systems, 2013, 37(1): 191-195. |
| [9] |
葛少云, 王龙, 刘洪, 等. 计及电动汽车入网的峰谷电价时段优化模型研究[J]. 电网技术, 2013, 37(8): 2316-2321. Ge Shaoyun, Wang Long, Liu Hong, et al. An optimization model of peak-valley price time-interval considering vehicle-to-grid[J]. Power System Technology, 2013, 37(8): 2316-2321. |
| [10] |
徐智威, 胡泽春, 宋永华, 等. 基于动态分时电价的电动汽车充电站有序充电策略[J]. 中国电机工程学报, 2014, 34(22): 3638-3646. Xu Zhiwei, Hu Zechun, Song Yonghua, et al. Coordinated charging strategy for PEV charging stations based on dynamic time-of-use tariffs[J]. Proceedings of the CSEE, 2014, 34(22): 3638-3646. |
| [11] |
黄润, 周鑫, 严正, 等. 计及电动汽车不确定性的有序充电调度策略[J]. 现代电力, 2012, 29(3): 57-63. Huang Run, Zhou Xin, Yan Zheng, et al. The controlled charging dispatch strategy by considering of the uncertainty of electric vehicles[J]. Modern Electric Power, 2012, 29(3): 57-63. DOI:10.3969/j.issn.1007-2322.2012.03.012 |
| [12] |
张振夫, 黄小庆, 曹一家, 等. 考虑分时电价的电动汽车充电负荷计算[J]. 电力自动化设备, 2014, 34(2): 24-29. Zhang Zhenfu, Huang Xiaoqing, Cao Yijia, et al. Charging load calculation considering TOU for electric vehicles[J]. Electric Power Automation Equipment, 2014, 34(2): 24-29. DOI:10.3969/j.issn.1006-6047.2014.02.005 |
| [13] |
赵伟, 姜飞, 涂春鸣, 等. 电动汽车充电站入网谐波分析[J]. 电力自动化设备, 2014, 34(11): 61-66. Zhao Wei, Jiang Fei, Tu Chunming, et al. Harmonic currents of grid-connected EV charging station[J]. Electric Power Auto-mation Equipment, 2014, 34(11): 61-66. DOI:10.3969/j.issn.1006-6047.2014.11.010 |
| [14] |
Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. DOI:10.1109/4235.996017 |
| [15] |
田立亭, 使双龙, 贾卓. 电动汽车充电功率需求的统计学建模方法[J]. 电网技术, 2010, 34(11): 126-130. Tian Liting, Shi Shuanglong, Jia Zhuo. A statistical model for charging power demand of electric vehicles[J]. Power System Technology, 2010, 34(11): 126-130. |
| [16] |
李秋硕, 肖湘宁, 郭静, 等. 电动汽车有序充电方法研究[J]. 电网技术, 2012, 36(12): 32-38. Li Qiushuo, Xiao Xiangning, Guo Jing, et al. Research on scheme for ordered charging of electric vehicles[J]. Power System Technology, 2012, 36(12): 32-38. |
| [17] |
刘青, 戚中译. 基于蒙特卡洛法的电动汽车负荷预测建模[J]. 电力科学与工程, 2014, 30(10): 14-19. Liu Qing, Qi Zhongyi. Electric vehicles load forecasting model based on Monte Carlo simulation[J]. Electric Power Science and Engineering, 2014, 30(10): 14-19. |
| [18] |
Clement Nyns K, Haesen E, Driesen J. The impact of charging plug-in hybrid electric vehicles on a residential distribution grid[J]. IEEE Transactions on Power Systems, 2010, 25(1): 371-380. DOI:10.1109/TPWRS.2009.2036481 |
 2018, Vol. 51
2018, Vol. 51




