武汉大学学报(工学版)   2016, Vol. 49 Issue (3): 429-434

文章信息

刘鹏, 郑景文
LIU Peng, ZHENG Jinwen
基于EMTDC的电压暂降概率评估的仿真分析
Simulation analysis of probabilistic assessment of voltage sags based on EMTDC
武汉大学学报(工学版), 2016, 49(3): 429-434
Engineering Journal of Wuhan University, 2016, 49(3): 429-434
http://dx.doi.org/10.14188/j.1671-8844.2016-03-019

文章历史

收稿日期: 2015-12-27
 Abstract              PDF               Figures               Tables
引用本文 0
刘鹏, 郑景文. 基于EMTDC的电压暂降概率评估的仿真分析[J]. 武汉大学学报(工学版), 2016, 49(3): 429-434.
LIU Peng, ZHENG Jinwen. Simulation analysis of probabilistic assessment of voltage sags based on EMTDC[J]. Engineering Journal of Wuhan University, 2016, 49(3): 429-434.
基于EMTDC的电压暂降概率评估的仿真分析
刘鹏, 郑景文     
武汉大学电气工程学院，湖北 武汉430072
收稿日期: 2015-12-27
作者简介: 刘鹏(1990-)，男，硕士，研究方向为电能质量分析、电压暂降的风险性评估、配电网故障定位等,E-mail:lp_whu_electrical@163.com..
摘要: 随着电压暂降在电能质量问题投诉比例中的不断增加，电压暂降的概率评估逐渐成为了电能质量研究中的一项重要内容.基于蒙特卡罗方法，建立了电力系统电压暂降故障信息的数学概率模型，在PSCAD/EMTDC仿真平台上，搭建了相关仿真模型，运用随机数模块和Channel Decoder组件对故障信息进行抽样和传送，并进行仿真计算，然后将计算结果进行统计，得到各负荷节点的电压暂降特征量和评估指标的概率分布，指出系统的薄弱环节，为电网故障造成的电压暂降的检测和补偿提供了依据.在IEEE14节点标准系统中验证了该方法的有效性.
关键词： 电压暂降     蒙特卡罗方法     PSCAD/EMTDC     建模     概率分布    
Simulation analysis of probabilistic assessment of voltage sags based on EMTDC
LIU Peng, ZHENG Jinwen     
School of Electrical Engineering, Wuhan University, Wuhan 430072,China
Abstract: As the increasing proportion of voltage sag in power quality complaints, the probabilistic assessment of voltage sag assessment is becoming an important part of the power quality study.A mathematical probability model of fault information of power system voltage sags is established based on the Monte Carlo method. Meanwhile, a related simulation model is built on PSCAD/EMTDC; the random numbers module and Channel Decoder component are used to send the fault information and make simulation calculation. Simultaneously, the calculation result is counted; and the probability distribution of voltage sag characteristics variable and evaluation index of load nodes are derived, pointing out the weaknesses of the system and providing basis for voltage sags detection and compensation caused by grid failure.The validity of the proposed method is proved in the standard IEEE-14 bus system.
Key words: voltage sags     Monte Carlo method     PSCAD/EMTDC     modeling     probability distribution    

目前，对电压暂降进行概率评估主要有三类方法：故障点法、临界距离法和蒙特卡罗法.文献[1]利用故障点法计算出了电压暂降的凹陷域.文献[2]基于故障点法，计算出了暂降幅值、持续时间等电压暂降特征量.文献[3]利用故障点法计算出了电压暂降发生的频率.但故障点法在计算之前就需要给出可能的故障点，而且评估结果与故障点选取的数量有关，因此，该方法具有一定的局限性.文献[4]基于临界距离法计算了某辐射状网络电压暂降的幅值和频次.但该方法的故障模型简单，仅适用于三相短路的分析.文献[5]对临界距离法进行了改进，使其能够适用于环状网络，但是故障的设置并不具有随机性.因此，临界距离法和故障点法均具有一定的局限性，而蒙特卡罗方法能够正确反映电力系统故障的随机性，而且采样次数与系统规模无关，具有较大的优越性.

本文提出在PSCAD/EMTDC平台基于蒙特卡罗方法建立故障信息的相关模型，运用随机数模块和Channel Decoder对故障信息进行抽样和传送，并进行仿真计算，经过统计得到了考察节点的电压暂降特征量和评估指标的概率分布，指出了系统的薄弱环节，为电网故障造成的电压暂降的检测和补偿提供了依据.

1 电压暂降分析的蒙特卡罗模型 1.1 电压暂降的特征量

电压暂降幅值、持续时间、发生频次是常用来描述电压暂降过程的3个参数[6].

通常用电压暂降时的电压有效值与额定电压有效值的比值来表示电压暂降的幅值，其变化范围为额定值10%~90%[7].IEEE将下降幅值在90%以上的情况视为正常电压，将下降幅值在10%以下的情况视为电压瞬时中断[8]，实质上，正常电压和电压瞬时中断是电压暂降的两种极端情况，可认为电压瞬时中断是幅值在10%以下的电压暂降[9].

电压暂降的持续时间为电力系统中继电保护装置允许故障电流通过的时间[10]，主要由保护装置的类型、正确动作情况和整定时间来决定.

电压暂降发生频次是反应电压暂降对电力用户影响频繁度的一个重要指标，指在一段时间内电压暂降发生的概率.

1.2 蒙特卡罗方法的概述

蒙特卡罗方法的基本原理是：用N个变量来控制一次随机过程的产生，运用蒙特卡罗方法来进行电压暂降的随机预估时，首先要建立各个故障状态变量的概率模型，然后由概率模型产生故障状态变量的随机抽样值，模拟故障的发生，反复N次随机抽样仿真计算，进而得到敏感负荷点的电压暂降特征[11].

1.3 故障状态变量的概率模型

在故障的概率模型中，故障信息主要包括：故障线路、故障位置、故障类型、故障起始时刻、故障持续时间等,通过蒙特卡罗模拟法随机产生确定.

1) 故障类型的概率模型

用随机方法产生每次的故障线路，设随机变量u1~(0,1)均匀分布，没有历史数据的情况下，可以假设第j条线发生故障的概率与线路的长度正比，即：

$P(j)=\frac{L(j)}{L}$    (1)

式中：L(j)为第j条线路的长度，j=(1,2,3,…,n);L为系统中所有线路长度之和.则故障线路的概率模型为

${{F}_{L}}=\left\{ \begin{align} & 1,\ \ u1 < P(1) \\ & 2,\ P(1)\le u1 < P(1)+P(2) \\ & 3,\ P(1)+P(2)\le u1 < P(1)+P(2)+P(3) \\ & \vdots \\ & N,\ P(1)+P(2)+P(3)+....+P(N-1)\le u1 < 1 \\ \end{align} \right.$    (2)

2) 故障点的概率模型

假设一条线路上每个点发生故障的概率是相同的，则产生随机数u2~(0,1)均匀分布，则Floc=Liju2代表故障点与线路左端点间的距离，其中，i表示线路的左端点，j表示线路的右端点.

3) 故障类型的概率模型

本文考虑10种不同情况的短路故障，故障类型由FT表示，FT从1到10分别表示A相短路接地、B相短路接地、C相短路接地、AB相短路接地、AC相短路接地、BC相短路接地、ABC三相短路接地、AB相短路、AC相短路、BC相短路.产生随机数u3~(0,1)均匀分布，则故障类型的概率模型为

${{F}_{T}}=\left\{ \begin{align} & 1,\ \ {{u}_{3}} < P({{F}_{T}}(1)) \\ & 2,\ P({{F}_{T}}(1))\le {{u}_{3}} < P({{F}_{T}}(1))+P({{F}_{T}}(2)) \\ & 3,\ P({{F}_{T}}(1))+P({{F}_{T}}(2))\le {{u}_{3}} < P({{F}_{T}}(1))+P({{F}_{T}}(2))+P({{F}_{T}}(3)) \\ & \vdots \\ & 10,\ P({{F}_{T}}(1))+P({{F}_{T}}(2))+....+P({{F}_{T}}(9))\le {{u}_{3}} < 1 \\ \end{align} \right.\ $    (3)

式中：P(FT(i))表示第i种类型的故障发生的概率(i=1,2,3,…,10).

4) 故障起始时刻的概率模型

在仿真中各节点电压在0.1 s后上升到稳定值，且仿真系统的频率为50 Hz，因此，引入随机数u4~(0.1,0.12)，可以模拟在一个电源周期内任意时刻发生故障.

5) 故障持续时间的概率模型

故障的持续时间用Rayleigh分布来模拟[12]，Rayleigh分布是仅含有一个参数K(K取10)的分布(与指数分布类似)，其概率密度函数为

$f(x)=Kx{{e}^{(-\frac{K{{x}^{2}}}{2})}}$    (4)

求得此密度函数的分布函数为

$F(x)=\int\limits_{0}^{x}{Kx{{e}^{-\frac{K{{x}^{2}}}{2}}}\text{d}x}=1-{{\text{e}}^{-\frac{K{{x}^{2}}}{2}}}$    (5)

求得此分布函数的反函数为

${{F}^{-1}}(x)=\sqrt{-2\ln (1-y)/K}$    (6)

令1－y=u5~(0,1)均匀分布，则短路持续时间T可表示为

$T=\sqrt{-2\ln ({{u}_{5}})/K}$    (7)

6) 故障电阻

本文假定故障电阻服从期望为5 Ω、标准差为1 Ω的正态分布[13].

1.4 电压暂降的评估指标

为了评估敏感负荷节点受电压暂降影响的程度，文献[14]提出了相应的概率评估指标，分别定义如下.

电压暂降幅值的期望值：

$\overline{{{U}_{i}}}=\sum\limits_{k=1}^{N}{{{U}_{ik}}}/N$    (8)

电压暂降持续时间期望值：

$\overline{{{T}_{i}}}=\sum\limits_{k=1}^{N}{{{T}_{ik}}}/N$    (9)

电压暂降能量指标：

${{W}_{i}}=(1-{{(\overline{{{U}_{i}}})}^{2}})\overline{{{T}_{i}}}$    (10)

式中：Uik为节点i第k次的电压暂降幅值,p.u.;Tik为节点i第k次的电压暂降持续时间,s;N为电压暂降总次数.

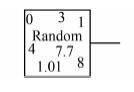
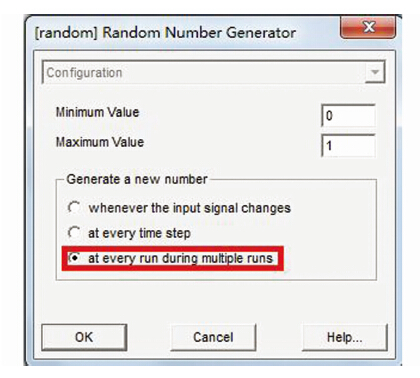
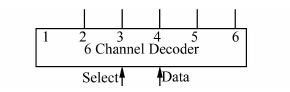
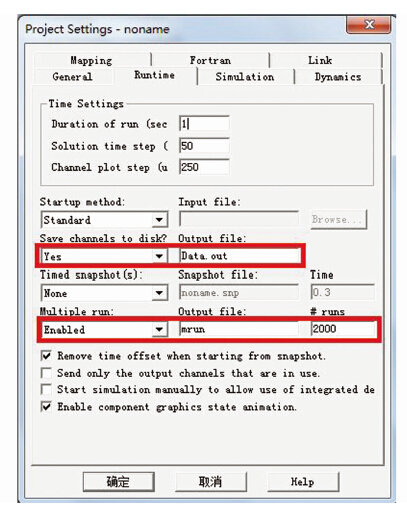
1.5 随机故障的仿真模拟

本文提出了一种随机故障模拟方法.采用随机数产生模块(如图 1)，对其进行相关设置(如图 2)使其在每一次模拟时都产生随机数，结合故障概率模型，确定故障信息，然后由Channel Decoder模块(如图 3)将故障信息传送到相应线路(该模块有6个传输端口，可对应6条线路，当系统线路数多于6时，需同时使用多个)，用来模拟系统随机故障.进行相关仿真设置(如图 4)，使仿真计算连续多次运行，并将结果数据记录.这样可使每次模拟的故障信息都是随机产生的，仿真计算在每次的抽样之后立即进行，满足蒙特卡罗方法的随机性要求，可真实地反映电力系统故障的随机性.

图 1 随机数模块 Figure 1 Random number module
图选项
图 2 随机数模块设置 Figure 2 Random number module setting
图选项
图 3 Channel Decoder模块 Figure 3 Channel Decoder module
图选项
图 4 仿真设置 Figure 4 Simulation setting
图选项
2 基于蒙特卡罗法的电压暂降概率评估流程

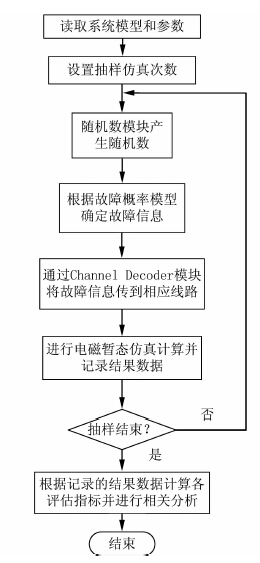
根据本文提出随机故障模拟方法，结合蒙特卡罗方法，得出电压暂降概率评估仿真流程如图 5.

图 5 电压暂降概率评估仿真流程 Figure 5 Simulation process of probabilistic assessment of voltage sags
图选项
3 算例分析

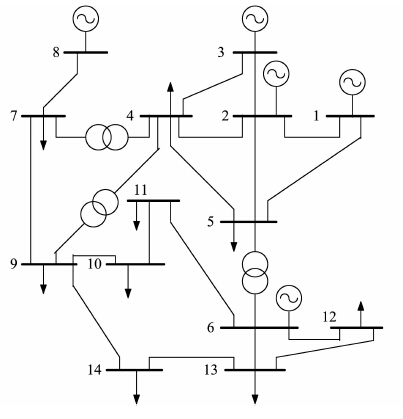
将本文所提电压暂降概率评估仿真方法用于IEEE14节点系统(如图 6)，具体参数见文献[15].综合考虑4种故障类型：单相接地，两相短路接地，两相相间短路，三相短路.假设单相接地故障的故障率为65%，两相短路接地故障率为20%，两相相间短路故障率为9%，三相短路故障率为6%[16].

图 6 IEEE14节点系统 Figure 6 IEEE14-node system
图选项

通过PSCAD/EMTDC仿真平台，结合本文提出的仿真方法，对目标系统进行2 000次仿真计算，并将结果数据进行统计分析.

3.1 故障状态变量的概率分布分析

故障状态变量的概率分布如图 7~11所示.

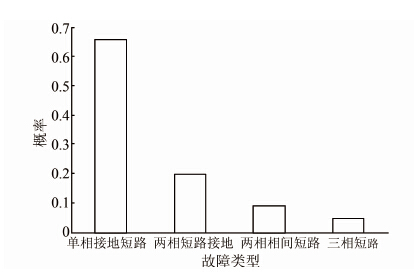
图 7 故障类型的概率分布 Figure 7 Probability distribution of fault types
图选项
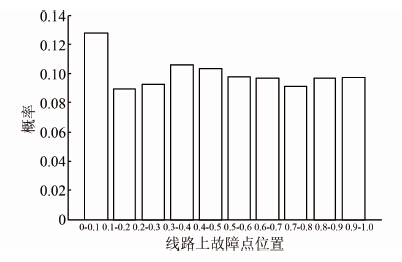
图 8 线路上故障点位置的概率分布 Figure 8 Probability distribution of fault locations on-line
图选项
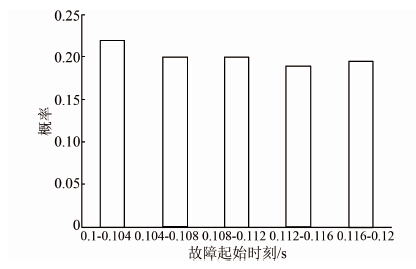
图 9 故障起始时刻的概率分布 Figure 9 Probability distribution of fault starting times
图选项
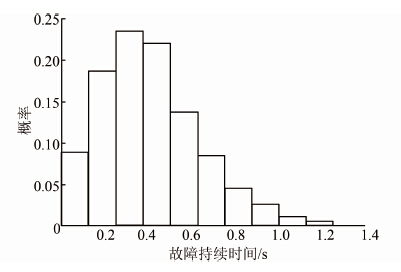
图 10 故障持续时间的概率分布 Figure 10 Probability distribution of fault durations
图选项
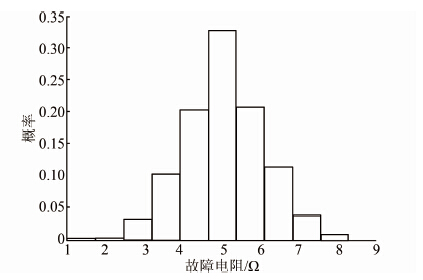
图 11 故障电阻的概率分布 Figure 11 Probability distribution of fault resistances
图选项

从图 7~11可以看出，各状态变量的概率分布结果与相应的数学概率模型是基本吻合的，从而表明本文提出的随机故障的模拟方法是准确的，仿真计算结果是可信的.

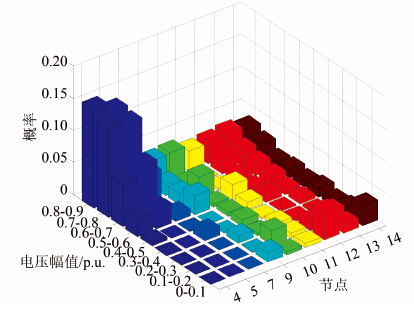
3.2 各节点处的电压暂降评估结果分析

把除了电源节点外的节点4、5、7、9、10、11、12、13、14这9个负荷节点作为考察点，将电压暂降幅值分为9个区间，用MATLAB做出节点号、暂降幅值、概率这3个量的三维分布图.

从图 12可看出：1) 节点4和5比其他节点发生电压暂降的概率都高出许多，说明节点4和5处的负荷更容易频繁受到电压暂降的影响.2) 节点12和14发生瞬时供电中断(U<0.1p.u.)的概率明显高出其他节点，说明节点12和节点14处的负荷很容易受到供电中断影响，这对于有高质量供电要求的用户来说是不允许的.

图 12 节点电压暂降幅值概率分布 Figure 12 Probability distribution of nodes voltage sag amplitudes
图选项
3.3 电压暂降评估指标分析

为了更准确地评估电压暂降情况，对式(8)~(10)的3个指标进行统计计算，结果如表 1所示.

表 1 各节点电压暂降评估指标 Table 1 Nodes assessment indices of voltage sags
节点45791011121314
Ui0.757 50.753 90.712 90.597 90.568 80.544 20.437 70.549 50.469 9
Ti0.414 70.410 30.417 80.410 40.415 60.434 30.405 20.405 20.406 8
Wi0.176 80.177 10.205 50.263 70.281 10.305 70.327 50.282 80.317 0
表选项

从表 1的统计计算结果可以看出：1) 各节点的电压暂降持续时间期望值差别不大，说明每个节点允许故障电流通过的时间是基本相等的.2) 所有节点的电压暂降幅值期望值均在0.8以下，总体来看，各个负荷节点的电压暂降都较为严重，需要采取相应措施进行不同程度的改善，同时再结合3.2中的分析，节点4和5发生电压暂降的概率还明显高于其他节点，因此节点4和5是系统中较为薄弱的环节，需要重点进行治理.3) 节点11、12、14的电压暂降能量指标均在0.3以上，说明在这3个节点处发生电压暂降时造成的能量损失较为严重，需要针对这几个位置采取相应的解决措施.

4 结论

本文提出了一种在PSCAD/EMTDC中运用随机数模块和Channel Decoder组件结合蒙特卡罗方法进行电压暂降概率评估的仿真计算方法.该方法可以较准确地模拟电力系统中的随机性故障.运用该方法对目标系统进行了多次抽样仿真计算，对结果进行了统计分析，得到了各负荷节点的电压暂降特征量和评估指标的概率分布，指出了系统的薄弱环节，为实际电网中由于随机故障造成的电压暂降的检测和补偿提供了依据.

参考文献
[1] Leborgne R C, Olguin G, Bollen M H J. Sensitivity analysis of stochastic assessment of voltage dips[C]//2004 International Conference on Power System Technology, IEEE, 2004, 1: 69-74.
[2] Goswami A K, Gupta C P, Singh G K. The method of fault position for assessment of voltage sags in distribution systems[C]//IEEE Region 10 and the Third International Conference on Industrial and Information Systems, IEEE, 2008:1-6.
[3] Baldwin T. Voltage sag analysis for making economic decisions on mitigation solutions[C]//Power Engineering Society Summer Meeting,IEEE, 1999: 482-483.
[4] Bollen M H J. The influence of motor reacceleration on voltage sags[J]. IEEE Transactions on Industry Applications, 1995, 31(4): 667–674. DOI:10.1109/28.395271
[5] Lim Y S, Strabc G. Analytical approach to probabilistic prediction of voltage sags on transmission networks[J]. Proc. Inst. Elect. Eng, Gen Transmission Distribution, 2002, 149(1): 7–14. DOI:10.1049/ip-gtd:20020008
[6] 肖湘宁, 韩民晓, 徐永海, 等. 电能质量分析与控制[M]. 2004.
Xiao Xiangning, Han minxiao, Xu Yonghai, et al. Analysis and Control of Power Quality[M]. Beijing: China Electric Power Press, 2004.
[7] 宋云亭, 郭永基, 张瑞华. 电压骤降和瞬时供电中断概率评估的蒙特卡罗仿真[J]. 电力系统自动化, 2003, 27(18): 47–51.
Song Yunting, Guo Yongji, Zhong Ruihua. Monte Carlo simulation of probabilistic assessment of voltage sag and power interruption[J]. Automation of Electric Power Systems, 2003, 27(18): 47–51.
[8] IEEE Recommended Practice on Monitoring Electric Power Quality Available[S].IEEE Std:1159-1994. http://grouper.ieee.org/groups/1159/docs/02WM.pdf
[9] 易杨, 张尧, 钟庆. 基于蒙特卡罗方法的大型电力用户电压暂降评估[J]. 电网技术, 2008, 32(6): 57–60.
Yi Yang, Zhong Rao, Zhong Qing. Assessment of voltage sags in large power consumer based on Monte Carlo method[J]. Power System Technology, 2008, 32(6): 57–60.
[10] 卢本初.配电系统电压骤降特性分析与可靠性评估[D].武汉:武汉大学,2004.
Lu Benchu. Characteristic analysis and reliability evaluation of voltage sag in distribution system [D].Wuhan: Wuhan University,2004. http://www.oalib.com/references/17645724
[11] 钟庆, 林凌雪, 易杨, 等. 电压暂降问题蒙特卡罗仿真模型比较[J]. 电力系统及其自动化学报, 2010, 22(6): 143–146.
Zhong Qing, Lin Lingxue, Yi Yang, et al. Comparisons among the Monte Carlo simulation models of voltage sags[J]. Proceedings of the CSU-EPSA, 2010, 22(6): 143–146.
[12] 要焕年, 曹梅月. 电力系统谐振接地[M]. 2000.
Yao Huannian, Cao Meiyue. Power System Resonant Grounded[M]. Beijing: China Electric Power Press, 2000.
[13] Juan A M, Jacinto M A. Voltage sags study in distribution networks-part III: voltage sag index calculation[J]. IEEE Trans on Power Delivery, 2006, 21(3): 1689–1697. DOI:10.1109/TPWRD.2006.874111
[14] Bollen M H J, Sabin D D, Thallam R S.Voltage-sag indices-recent developments in IEEE PI564 task force[C]//Quality and Security of Electric Power Delivery Systems,CIGRE/IEEE PES International Symposium, IEEE, 2003:34-41.
[15] IEEE14-Bus Test Case[EB/OL].Available：http://www.ee.washington.edu/research/pstca/pf14/pg_tca14bus.htm.
[16] Billinton R, Kumar S, Chowdhury N, Chu K. A reliability test system for educational purposes-basic data[J]. IEEE Transactions on Power Systems, 1989, 4(3): 1238–1244. DOI:10.1109/59.32623