基于BP神经网络的配电网项目建设效果后评价方法

文章信息

关朝杰, 李秋燕, 郭新志, 陈江涛, 胡钋, 殷奕恒, 杨丰阁

GUAN Chaojie, LI Qiuyan, GUO Xinzhi, CHEN Jiangtao, HU Po, YIN Yiheng, YANG Fengge

A post-evaluation method for effect of distribution network project construction based on back propagation neural network

武汉大学学报(工学版), 2018, 51(3): 232-238,267

Engineering Journal of Wuhan University, 2018, 51(3): 232-238,267

http://dx.doi.org/10.14188/j.1671-8844.2018-03-008

文章历史

收稿日期: 2017-11-20

Abstract

PDF

Figures

Tables

引用本文

关朝杰, 李秋燕, 郭新志, 陈江涛, 胡钋, 殷奕恒, 杨丰阁. 基于BP神经网络的配电网项目建设效果后评价方法[J]. 武汉大学学报(工学版), 2018, 51(3): 232-238,267. 复制到剪切板

GUAN Chaojie, LI Qiuyan, GUO Xinzhi, CHEN Jiangtao, HU Po, YIN Yiheng, YANG Fengge. A post-evaluation method for effect of distribution network project construction based on back propagation neural network[J]. Engineering Journal of Wuhan University, 2018, 51(3): 232-238,267. 复制到剪切板

基于BP神经网络的配电网项目建设效果后评价方法

关朝杰¹, 李秋燕¹, 郭新志¹, 陈江涛¹, 胡钋², 殷奕恒², 杨丰阁²

1. 国网河南省电力公司经济技术研究院, 河南郑州 450052;
2. 武汉大学电气工程学院, 湖北武汉 430072

收稿日期：2017-11-20

作者简介：关朝杰(1987-)，男，硕士，工程师，主要从事配电网规划技术研究，E-mail:guanchaojie@ha.sgcc.com.cn.

通讯作者：胡钋(1965-)，男，教授，博士生导师，主要从事电力系统及其自动化研究，E-mail:phu1126@126.cm

基金项目：国家自然科学基金项目(编号：51567018).

摘要：针对配电网项目的建设效果，建立了一套科学完备的后评价指标体系；基于BP人工神经网络，建立了具有L个隐含层节点、3层网络的配电网项目建设效果后评价模型，以配电网建设成效指标数据为样本作为输入即可得到建设效果的评价结果.以某省县域配电网为例，利用Matlab软件对BP神经网络进行训练与检验，结果表明所建立的BP神经网络模型对检验样本的模拟输出和期望输出是一致的；应用该模型测试样本得出的评价结果与模糊综合评价结果基本一致，表明所述方法是准确与可行的.

关键词：配电网项目后评价建设效果指标体系 BP人工神经网络

A post-evaluation method for effect of distribution network project construction based on back propagation neural network

GUAN Chaojie¹, LI Qiuyan¹, GUO Xinzhi¹, CHEN Jiangtao¹, HU Po², YIN Yiheng², YANG Fengge²

1. State Grid Henan Economic Research Institute, Zhengzhou 450052, China;
2. School of Electrical Engineering, Wuhan University, Wuhan 430072, China

Abstract: This paper has established a set of scientific and complete post-evaluation index system, in light of the construction effect of the distribution network project. Based on the back propagation (BP) artificial neural network, the post-evaluation model of the construction effect of the distribution network project with L hidden layer nodes and 3-layer network is established. The evaluation results of the construction effect can be obtained by using the data of the distribution network construction performance indicators as input. Taking a provincial distribution network for example, the BP neural network is trained and tested by Matlab software. The results show that the established BP neural network model's output of the test sample is consistent with the expected output; and compared with the application of the model test samples obtained from the evaluation results and fuzzy comprehensive evaluation results are basically the same, so as to show the accuracy and feasibility of the method described in this paper.

Key words: post-evaluation of distribution network project construction effect index system back propagation (BP) artificial neural network

项目后评价是项目周期中最后一个重要环节，是项目竣工交付运行一段时间后，对项目进行全面评价的一项工作，后评价在国内外部分行业已经开展很长时间，并取得了良好的效果.然而，国内开展电网项目后评价工作的时间较短，且重点集中于主网工程项目的后评价，对配电网工程项目的后评价尚处于起步阶段.目前仅南方电网公司颁布实施了《配电网项目后评价实施办法》(Q/CSG21301-2010)，涉及到从项目过程、项目建设效果、经济效益等方面，对配电网工程项目进行后评价，其中的核心部分就是配电网建设效果的后评价，在理论研究和工程实际中都具有重要的意义^{[1, 2]}.文献[3]对配电网项目后评价方法进行了归纳总结，然而并没有提出一套科学完备的评价体系；文献[4]对配电网建设改造项目投资效果后评价建立了一套较为完备的指标体系，然而其权重求取方法仅为层次分析法，过于片面；文献[5]应用模糊综合评价模型对输变电工程的经济效益进行了后评价；文献[6]建立了一套完备的电网建设项目后评价指标体系，并应用基于ANP的多层次模糊综合评价方法对指标进行赋权与评分，但是该方法主观性太强；文献[7, 8]对配网建设功能效果进行专项后评价研究，对传统的逻辑框架法进行了改进，引入后评价中的前后对比和有无对比思想，更加明确地反映了项目预期指标的实现情况，然而该方法主观性也过强.本文提出了一种基于BP神经网络模型的配电网项目建设效果后评价方法，该方法将往年的配电网项目建设效果后评价指标的数据与往年的专家评分结果进行拟合训练，将训练得到的模型应用于现年的配电网项目建设效果后评价；由于其能够充分吸收专家的判断经验，从而省去了专家赋权与打分的步骤，使评价更加简洁明了.此外，所建立的模型可以对指标数据作出较为准确的判断.

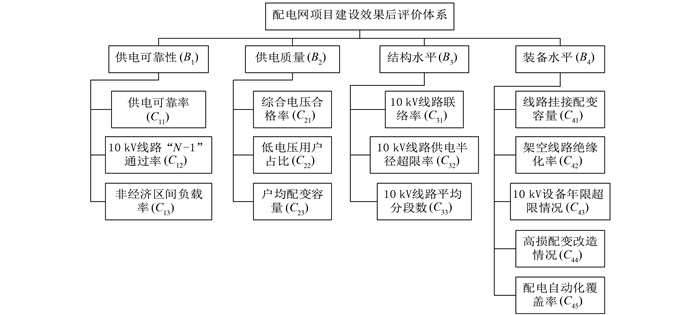
1 配电网项目建设效果后评价指标体系

配电网项目建设效果后评价的准确性，在很大程度上取决于后评价指标体系的构建原则与方法.因此，必须建立一套科学、完备的后评价指标体系.本文基于现有配电网项目后评价方面的研究成果^{[1, 2, 9, 10, 11, 12]}，本着指标体系制定的科学性、可操作性、可量化与可拓展性原则，结合配电网项目的特征，构建了一套配电网项目建设效果后评价指标体系，如图 1所示.它不仅能够全面反映配电网项目的建设效果，而且其结合数据采集难度等实际情况进行合理构建，既保证指标体系的简洁性又体现出层次感.表 1为配电网项目建设效果后评价指标体系的评价准则.

图 1 配电网项目建设效果后评价体系 Figure 1 Distribution network project construction effect evaluation system

图选项

表 1 评价指标体系评分标准 Table 1 Evaluation index system score standard

评价标准	配电网项目建设效果后评价指标体系
	B₁			B₂			B₃			B₄
	C₁₁ /%	C₁₂ /%	C₁₃ /%	C₂₁ /%	C₂₂ /%	C₂₃ /kVA	C₃₁ /%	C₃₂ /%	C₃₃	C₄₁ /MVA	C₄₂ /%	C₄₃ /%	C₄₄ /%	C₄₅ /%
100	100	100	0	100	0	3.0	100	0	4	1	70	0	70	100
80	99	70	8	99	10	2.5	60	10	3或5	3	50	40	50	80
60	97.5	40	15	97.5	20	1.5	30	20	2.5或5.5	6	30	30	30	60
40	96	20	30	96	30	1.2	20	30	2或6	9	20	20	20	40
20	94	10	50	94	40	0.8	10	60	1.5或6.5	12	10	10	10	20
0	90	0	60	90	50	0.4	0	100	1或7	18	0	50	0	0

表选项

2 配电网项目建设效果后评价的BP神经网络模型

配电网项目建设效果后评价属于数据拟合问题，它是将往年的配电网项目建设效果后评价指标体系的实际数据与对应年份的专家评分结果进行拟合训练后，将所得到的训练后的模型应用于现年的配电网项目建设效果后评价中.BP神经网络模型是目前应用最为广泛的网络模型，通过它能够很好地解决数据拟合问题，即很好地实现配电网项目建设效果的后评价.然而标准BP神经网络模型存在许多缺陷，例如：学习过程收敛速度慢；易陷于局部最小值而不能保证全局最优；隐含层层数与节点数如何确定等等^[13-15].所以需要对BP神经网络作出优化设计.

2.1 BP神经网络优化算法原理

BP神经网络算法最突出的问题是收敛速度较慢，标准BP神经网络算法(下降梯度算法)收敛速度太慢，甚至会失去实用价值；Gauss-Newton算法收敛速度快，但在线性方程组求解时容易出现非正定矩阵和奇异矩阵，且对初始参数值敏感，可能存在无法收敛的情况.可采用Levenberg-Marquardt(LM)算法来优化标准BP神经网络算法.LM算法实际上是自适应学习率-动量梯度下降算法和Gauss-Newton算法的结合，其优点在于网络规模较小时收敛非常迅速.LM算法的基本思想是使其每次迭代不再沿着单一的负梯度方向，而是允许误差沿着恶化方向进行搜索，同时通过在自适应学习率-动量梯度下降算法和Gauss-Newton算法之间自适应调整来优化网络权值，使其能够有效收敛，从而大大提高了网络的收敛速度和泛化能力.

设误差函数为

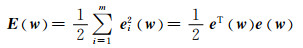(1)

式中：

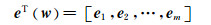(2)

w(k)代表第k次迭代的权值、阈值向量，则

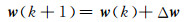(3)

Gauss-Newton算法是根据二阶导数信息调整权值大小，对误差函数E(w)按二阶泰勒公式展开，得到

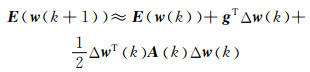(4)

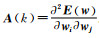
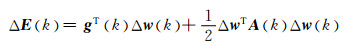式中：g^T(k)是E(w)的梯度向量; A(k)是E(w)的Hessian矩阵，其元素值为E(w)对各权值的二阶导数，即.权值修正后的误差函数变化量为

(5)

要获得式(5)中ΔE(k)的最小值，需要满足：

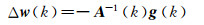(6)

这就是Gauss-Newton算法的基本原理，即

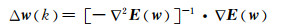(7)

式中：▽E(w)表示梯度向量；▽²E(w)表示误差函数E(w)的Hessian矩阵.

E(w)的梯度向量为

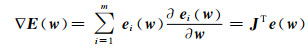(8)

式中：J^T(w)是Jacobian矩阵，即

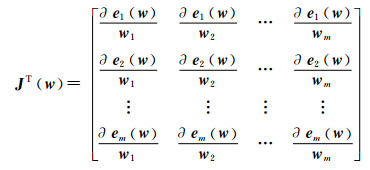(9)

E(w)的Hessian矩阵为

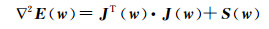(10)

式中: ，▽²e_i(w)是e_i(w)的Hessian矩阵.

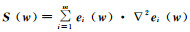
在靠近极值点时S(w)≈0，将Gauss-Newton算法修正为

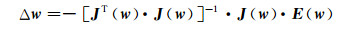(11)

LM算法对Gauss-Newton算法又进行了调整，调整后的权值规则为

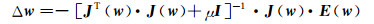(12)

式中:Δw是权值、阈值向量的调整增量; e是误差向量; J是误差对权值阈值的Jacobian矩阵; μ为标量; I为单位矩阵.在学习过程中，μ值决定了学习算法的性质.若μ值增加，学习过程主要依据具有较小学习速率的自适应学习率-动量梯度下降算法进行；若μ值减小到零时，学习算法就变为Gauss-Newton算法进行，由于矩阵J^TJ+μI是正定的，式(12)的解总是存在.LM算法在自适应学习率-动量梯度下降算法与Gauss-Newton算法之间平滑调和，若满足期望误差、达到最大训练次数、或μ达到最大值，则网络停止训练.

2.2 BP神经网络设计 2.2.1 数据预处理

相关研究表明^[16]，BP人工神经网络模型的训练样本过少会造成模型的鲁棒性、适用性较差，因而无法对实测数据做出准确识别.为了避免这一问题，在进行数据分析时，用Matlab软件中的normrnd函数，根据数据呈正态分布的原则生成N个总样本，对样本进行扩充，再从中抽取N_train(N_train≥N×70%)个训练样本，N_examine(N_examine≥N×10%)个检验样本和N_test(N_test≥N×10%)个测试样本，从而提高BP人工神经网络模型的鲁棒性.并且，为了便于利用Matlab nntool工具箱中的训练函数，应用最大最小函数premnmx对训练样本、检验样本进行预处理，将样本数据量化到[-1, 1]内作为输入单元.

2.2.2 网络拓扑结构

网络拓扑结构主要包括网络层数、输入层节点数、隐含层节点数、输出层节点数，下面分别予以说明.

1) 网络层数

文献[17]指出：单个隐含层的网络可以通过适当增加节点数实现任意非线性映射.因此，配电网项目建设效果后评价模型只需要一个隐含层.

2) 输入层节点数

一般而言，输入层节点数n取决于输入向量的维数，即配电网项目建设效果后评价指标体系中的指标数.

3) 隐含层节点数

隐含层节点数对网络的性能有很大影响.目前尚无理想的解析式用以确定合理的隐含层节点个数.通常是利用经验公式给出其估计值，本文采用另一种确定隐含层节点数的方法，即首先在网络中加入足够多的隐含层节点(L≤n)，再通过学习将不起作用的节点剔除，达到最优训练时间与精度为止.相反，也可以在开始时加入少量节点，在学习到一定次数后，若训练效果不佳再适当增加节点，直到取得比较合理的效果为止.

4) 输出层节点数

输出层节点数m同样需要根据实际问题来确定.由于本文BP神经网络的目标输出为配电网项目建设效果后评价结果，因此输出层节点数取1.

2.2.3 网络初始权值

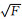
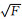
对于BP网络初始值，应选取均匀分布的小的随机数，其经验值一般位于(-2.4/F, 2.4/F)或者(-3/, 3/)范围内，其中F为权值输入端连接的节点数.

2.2.4 传递函数和训练算法

BP神经网络节点间的传递函数一般选取可微的单调递增函数，文献[18]指出当输入层到隐含层间的传递函数为tansig，隐含层到输出层间的传递函数为purelin时误差百分比和均误差对BP网络模型的影响最小，故本文选取隐含层函数为tansig，输出层函数为purelin，训练算法为LM优化算法.

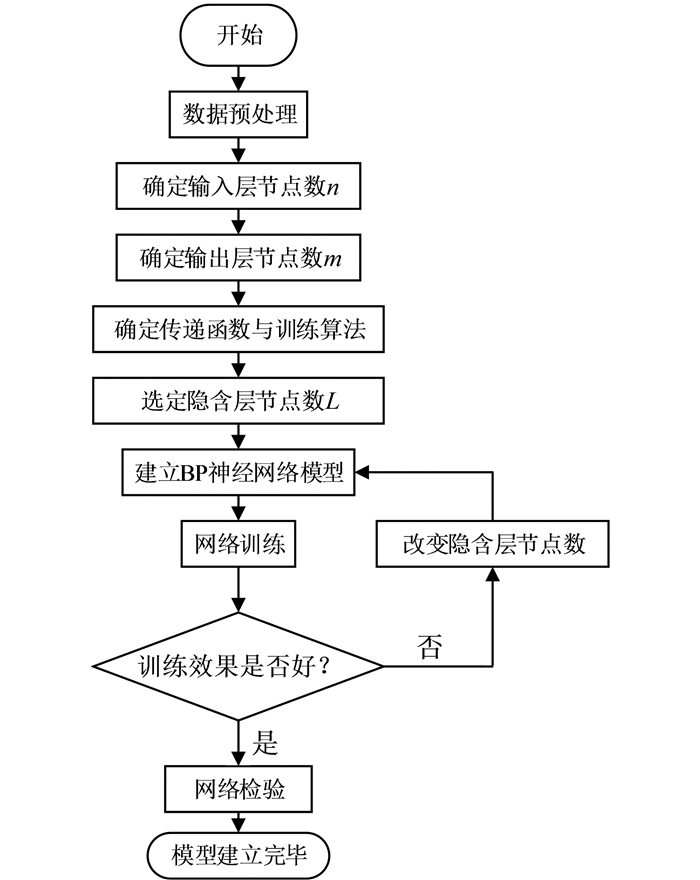
2.2.5 网络模型的训练与检验

依据上述BP神经网络的网络结构、传递函数和训练方法，利用Matlab软件中的nntool工具箱建立其BP神经网络模型(拓扑结构为n-L-m)，并对其进行训练和检验.BP神经网络模型建立流程如图 2所示.

图 2 BP神经网络模型建立流程 Figure 2 Back propagation neural network model establishment flowchart

图选项

3 算例分析

本文以某省县域配电网为例，建立适用于该省县域配电网项目建设效果后评价模型.通过所构建的配电网项目建设效果后评价指标体系，并收集该省108个县2015年的指标原始数据以及各地区该年的专家评分结果，以这些数据为基准建立适用于该省县域配电网的基于BP人工神经网络的评价模型.

3.1 建立模型 3.1.1 数据处理

本文对该省108个县进行数据采集分析，用Matlab软件的normrnd函数，根据数据呈正态分布的原则生成400个总样本，对108个样本进行扩充，再从中抽取76个训练样本，16个检验样本，16个测试样本，应用最大最小函数premnmx对训练样本、检验样本进行预处理，将参数量化到[-1, 1]内再作为输入单元.

3.1.2 确定BP神经网络拓扑结构

本文配电网项目功能效果后评价建立的BP网络模型层数取3层.由于指标体系的指标个数为14，所以输入层节点数为14；网络的输出为评价结果，故而输出层节点数为1；通过网络训练检验如表 2所示.当隐含层节点数为13时网络的收敛速度最快、精度最高，于是隐含层节点数取13.因此，模型的拓扑结构为14-13-1.

表 2 不同隐含层节点下的网络收敛速度与精度 Table 2 Network convergence speed and precision under different hidden layers

隐含层节点数	11	12	13	14	15
收敛速度	10	9	9	9	10
相关系数	0.954 05	0.977 87	0.998 18	0.989 48	0.974 37

表选项

3.1.3 选取传递函数与训练参数

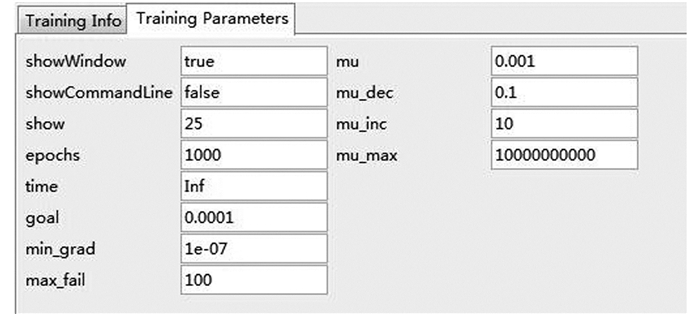
输入层到隐含层采用tansig函数，而输出层则使用线性purlin函数，训练算法选取LM算法，训练参数如图 3所示.

图 3 BP神经网络的训练参数 Figure 3 Training parameters of back propagation neural network

图选项

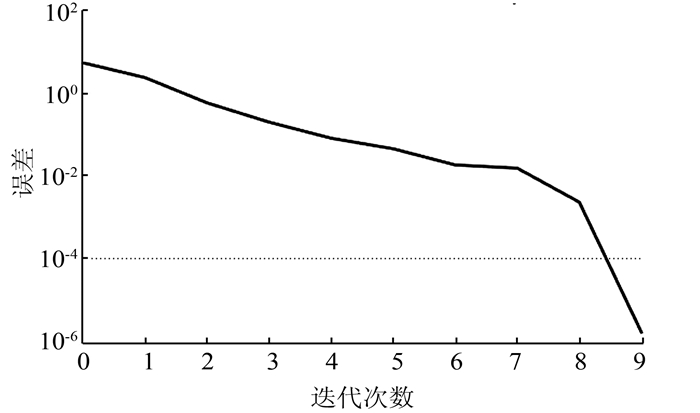
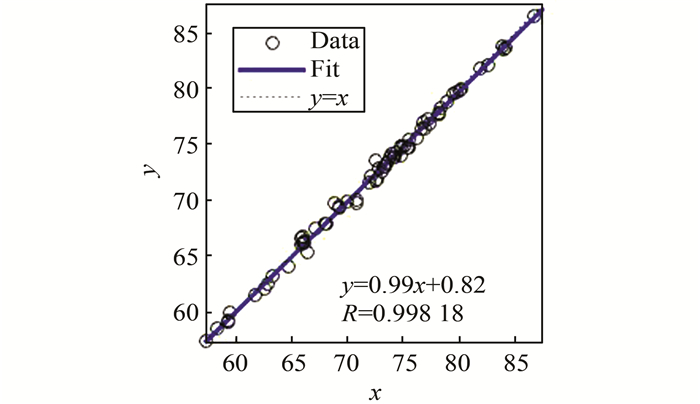
在Matlab命令窗口输入nntool，通过GUI界面，依据上述神经网络结构、传输函数和参数设置，建立配电网项目建设效果后评价的BP人工神经网络模型，对其进行训练和检验.通过训练发现网络仅经过了13次迭代就达到了期望的误差水平，如图 4所示，这说明模型的收敛速度是非常快的，其训练样本数据回归情况如图 5所示，可以看出目标响应与仿真输出效果非常好，相关系数达到了0.998 18，说明模型的拟合程度非常高.

图 4 网络训练收敛图 Figure 4 Network training convergence map

图选项

图 5 BP神经网络数据回归 Figure 5 Back propagation neural network data regression

图选项

用训练好的BP神经网络模型对检验样本进行仿真，将模拟结果数值和期望结果进行比较，从表 3可以看出，神经网络模拟结果的误差在1%左右，说明此神经网络的仿真效果较好，适合用于配电网项目建设效果后评价.

表 3 检验样本仿真结果与期望结果的对比 Table 3 Comparison between test sample simulation results and expected results

检验样本	C₁₁ /%	C₁₂ /%	C₁₃ /%	C₂₁ /%	C₂₂ /%	C₂₃ /kVA	C₃₁ /%	C₃₂ /%	C₃₃	C₄₁ /MVA	C₄₂ /%	C₄₃ /%	C₄₄ /%	C₄₅ /%	网络模拟结果	期望结果	误差 /%
1	99.92	38.90	5.19	98.84	15.31	1.11	53.20	7.79	1.77	5.48	5.45	3.46	42.07	8.17	73.86	73.96	-0.14
2	99.77	23.00	18.00	98.93	16.47	1.55	49.00	27.00	2.30	5.35	0.81	12.00	26.97	1.21	74.49	74.85	-0.48
3	99.01	5.00	10.92	99.46	11.85	1.31	20.17	16.38	1.26	5.40	19.28	7.28	69.98	28.92	85.74	85.19	0.64
4	99.93	9.68	22.58	98.96	16.42	0.96	9.68	33.87	2.00	5.89	0.97	15.05	82.58	1.46	76.13	76.02	0.14
5	98.98	37.83	4.05	99.21	16.00	1.23	52.70	6.08	2.27	5.07	2.67	2.70	66.57	4.01	70.97	70.44	0.75
6	99.89	24.00	1.00	98.95	10.89	1.03	35.00	1.50	2.00	5.53	23.09	0.67	43.41	34.64	88.58	88.96	-0.43
7	98.77	51.35	9.46	99.20	13.33	0.98	51.35	14.19	0.78	6.95	13.36	6.31	1.33	20.04	76.54	76.50	0.05
8	99.90	8.08	10.10	98.20	16.64	0.77	8.08	15.15	1.70	5.81	0.11	6.73	29.64	0.17	79.91	80.92	-1.26
9	99.81	36.00	5.80	99.20	14.65	1.20	39.50	8.70	2.00	7.49	8.08	3.87	59.48	12.12	87.86	86.79	1.22
10	99.75	13.56	1.70	98.92	14.77	1.12	13.56	2.55	3.00	5.51	7.60	1.13	57.12	11.40	80.12	79.68	0.55
11	99.80	1.92	26.92	99.90	10.82	1.50	16.67	40.38	1.42	6.20	23.39	17.95	28.57	35.08	71.53	71.19	0.48
12	99.95	45.76	2.00	98.92	11.85	1.33	49.15	3.00	2.00	5.03	19.28	1.33	31.70	28.92	79.49	80.30	-1.02
13	99.84	19.98	19.30	99.00	14.65	1.51	27.00	28.95	2.13	9.10	8.08	12.87	36.54	12.12	86.47	86.56	-0.10
14	99.90	65.00	0.00	98.93	16.10	0.99	68.00	0.00	2.30	6.10	2.27	0.00	3.24	3.41	79.45	80.79	-1.69
15	99.92	20.43	16.12	99.21	11.53	1.53	30.86	24.18	3.23	12.22	20.55	10.75	25.27	30.83	79.15	80.08	-1.17
16	99.88	20.00	12.31	98.98	10.89	1.39	20.00	18.47	2.13	6.64	23.09	8.21	16.55	34.64	83.89	83.18	0.85

表选项

3.2 模型应用

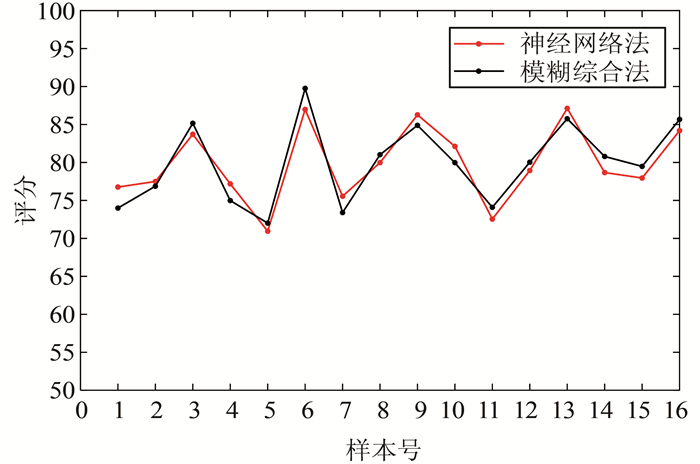
用训练好的BP神经网络模型对该省几个县的配电网项目建设效果进行综合评价.将表 4中测试样本(16个县)的指标数据通过Matlab最大最小函数premnmx处理后得到的预处理数据作为BP人工神经网络的输入，得出输出结果如图 6所示.

表 4 测试样本的指标数据 Table 4 Indicator data of test samples

测试样本	C₁₁ /%	C₁₂ /%	C₁₃ /%	C₂₁ /%	C₂₂ /%	C₂₃ /kVA	C₃₁ /%	C₃₂ /%	C₃₃	C₄₁ /MVA	C₄₂ /%	C₄₃ /%	C₄₄ /%	C₄₅ /%
1	98.79	21.00	1.10	99.20	14.00	0.95	23.00	1.65	2.00	6.34	10.68	0.73	4.02	16.02
2	98.77	36.53	22.70	99.20	6.72	0.93	44.20	34.05	3.00	8.07	39.77	15.13	58.69	59.66
3	99.84	42.92	0.00	99.07	13.27	1.07	58.00	0.00	7.50	7.24	13.59	0.00	55.78	20.38
4	99.10	25.00	4.10	99.15	12.61	0.98	25.00	6.15	2.11	8.06	16.23	2.73	20.25	24.35
5	98.85	18.00	15.07	99.35	10.56	0.91	26.00	22.61	2.40	7.98	24.42	10.05	78.46	36.63
6	99.85	30.00	6.02	99.05	13.27	0.86	45.78	9.03	1.47	5.29	13.59	4.01	53.51	20.38
7	99.37	25.00	15.00	99.91	13.27	1.00	29.88	22.50	2.30	9.17	13.59	10.00	26.62	20.38
8	99.90	18.40	19.30	99.03	15.96	1.49	24.50	28.95	1.42	11.90	2.83	12.87	12.70	4.24
9	99.89	13.20	0.00	98.93	9.06	1.17	15.20	0.00	1.80	5.09	30.42	0.00	16.07	45.63
10	99.93	21.90	7.02	98.99	15.96	0.93	43.90	10.53	3.00	35.99	2.85	4.68	69.50	4.27
11	99.07	8.60	22.70	99.40	10.75	1.00	44.20	34.05	1.94	13.23	23.67	15.13	24.88	35.51
12	99.91	16.28	26.92	98.96	15.62	1.19	22.00	40.38	2.00	8.30	4.20	17.95	63.29	6.30
13	99.89	52.20	6.50	98.84	16.08	0.92	51.00	9.75	1.70	4.76	2.36	4.33	30.49	3.54
14	99.89	23.68	28.95	98.92	14.75	1.08	34.21	43.43	1.89	8.24	7.67	19.30	55.30	11.50
15	99.94	21.68	19.56	99.01	16.64	0.93	30.43	29.34	1.85	9.26	0.11	13.04	80.52	0.17
16	99.98	14.29	21.69	99.84	13.07	1.02	14.29	32.54	3.30	2.42	14.38	14.46	3.89	21.57

表选项

由图 6可知，该省的16个县的配电网项目建设效果评分均在80分左右，可见该年该省16个县的配电网建设效果很好，且其建设效果状况也较为接近，说明该省对县域配电网的投资建设效果明显.再对比模糊综合评价法，也可看出神经网络的仿真结果与模糊综合评价基本一致，由于应用模糊综合评价法会消耗大量人力物力，因此运用神经网络模型进行评价具有经济好的特点.

图 6 测试样本评价结果对比图 Figure 6 Comparison of test sample evaluation results chart

图选项

4 结论

本文提出了一种基于BP神经网络的配电网项目建设效果后评价方法，通过构建评价指标体系，确定神经网络的类型和结构，应用Matlab神经网络拟合工具箱(nntool)训练网络搭建模型，最后应用评价模型对某省县域数据进行评价，并与模糊综合评价方法进行对比，证明BP神经网络方法能够避免人为确定各指标的权重带来的主观性，从而提高评价结果的准确性，并充分吸收专家的判断经验，对样本数据作出较为准确的判断，证实了运用人工神经网络方法进行配电网项目建设效果后评价的可行性和准确性.

参考文献

[1]	徐振超. 配电网投资项目后评价研究[D]. 长沙: 湖南大学, 2014. Xu Zhenchao. Research on distribution project investment evaluation[D]. Changsha: Hunan University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10532-1014301240.htm

[2]	何滢. 配电网项目后评价研究及应用[D]. 北京: 华北电力大学, 2012. He Ying. Research and application of distribution network project post evaluation[D]. Beijing: North China Electric Power University, 2012.

[3]	赵柯. 配电网项目后评价方法浅析[J]. 科学大众, 2013(2): 170. Zhao Ke. Post evaluation method of distribution network project analysis[J]. Popular Science, 2013(2): 170.

[4]	喻刚. 配电网建设改造项目投资效果后评价方法研究[J]. 价值工程, 2013(12): 324–325. Yu Gang. Study on post-evaluation method of investment effect of investment in distribution networks[J]. Value Engineering, 2013(12): 324–325. DOI:10.3969/j.issn.1006-4311.2013.12.176

[5]	李君宏. 基于模糊综合评价的输变电工程经济效益后评价研究[J]. 华北电力大学学报(社会科学版), 2012(5): 42–44. Li Junhong. Study on post-evaluation of economic benefits for the power transmission and transformation project based on fuzzy comprehensive evalution[J]. Journal of North China Electic Power University(Social Science), 2012(5): 42–44.

[6]	徐志勇, 张徐东, 曾鸣, 等. 基于ANP的多层次模糊综合评价法的电网建设项目后评价研究[J]. 华东电力, 2003, 37(3): 488–490. Xu Zhiyong, Zhang Xudong, Zeng Ming, et al. Application of ANP based multi-level fuzzy comprehensive evaluaiton methods to post-evaluation for grid construction projects[J]. East China Electric Power, 2003, 37(3): 488–490.

[7]	吴鸿亮. 改进的逻辑框架法在电网项目后评价中的应用[J]. 电网与清洁能源, 2011, 27(10): 4–7, 12. Wu Hongliang. Application of improved LFA in post-evaluation for power grid projects[J]. Power System and Clean Energy, 2011, 27(10): 4–7, 12. DOI:10.3969/j.issn.1674-3814.2011.10.002

[8]	吴鸿亮. 配网投资建设功能效果后评价[J]. 南方电网技术, 2010, 4(增刊1): 32–35. Wu Hongliang. Study on post-evaluation of function effects of investment in distribution network[J]. Southern Power System Technology, 2010, 4(Supplement 1): 32–35.

[9]	廖造壮, 陈悦华, 蒙环宁. 电网建设项目后评价指标体系研究[J]. 项目管理技术, 2012, 10(1): 29–33. Liao Zaozhuang, Chen Yuehua, Meng Huanning. Research on post evaluation index system of power grid construction project[J]. Project Management Technology, 2012, 10(1): 29–33.

[10]	李振宇, 江伟. 输变电项目后评价指标体系构建[J]. 科技信息, 2009(15): 720, 668. Li Zhenyu, Jiang Wei. Post evaluation index system construction for power transmission and transformation project[J]. Science & Technology Information, 2009(15): 720, 668.

[11]	詹智红, 周明, 武强, 等. 电网建设项目后评价指标体系及其评价方法研究[J]. 湖北电力, 2015, 39(2): 63–66. Zhan Zhihong, Zhou Ming, Wu Qiang, et al. Post evaluation index system and evaluation method of power grid construction project[J]. Hubei Electric Power, 2015, 39(2): 63–66.

[12]	叶倩容. 广州供电局10 kV及以下配网投资项目后评价指标体系研究[J]. 科技信息, 2009(31): 302–303. Ye Qianrong. Study on post evaluation index system for distribution network investment project of 10 kV and below in Guangzhou Power Supply Bureau[J]. Science & Technology Information, 2009(31): 302–303.

[13]	许童羽, 马艺铭, 曹英丽, 等. 基于主成分分析和遗传优化BP神经网络的光伏输出功率短期预测[J]. 电力系统保护与控制, 2016, 44(22): 90–95. Xu Tongyu, Ma Yiming, Cao Yingli, et al. Short term forecasting of photovoltaic output power based on principal component analysis and genetic optimization of BP neural network[J]. Power System Protection and Control, 2016, 44(22): 90–95. DOI:10.7667/PSPC160074

[14]	王新普, 周想凌, 邢杰, 等. 一种基于改进灰色BP神经网络组合的光伏出力预测方法[J]. 电力系统保护与控制, 2016, 44(18): 81–87. Wang Xinpu, Zhou Xiangling, Xing Jie, et al. A prediction method of PV output power based on the combination of improved grey back propagation neural network[J]. Power System Protection and Control, 2016, 44(18): 81–87. DOI:10.7667/PSPC151675

[15]	姚仲敏, 潘飞, 沈玉会, 等. 基于GA-BP和POS-BP神经网络的光伏电站出力短期预测[J]. 电力系统保护与控制, 2015, 43(20): 83–89. Yao Zhongmin, Pan Fei, Shen Yuhui, et al. Short term output forecast of photovoltaic plant based on GA-BP and POS-BP neural networks[J]. Power System Protection and Control, 2015, 43(20): 83–89. DOI:10.7667/j.issn.1674-3415.2015.20.013

[16]	李欣, 刘崇明, 陈运辉. 基于BP神经网络的火电厂技改项目成功度后评价研究[J]. 华东电力, 2010, 38(9): 1432–1435. Li Xin, Liu Congming, Chen Yunhui. Study on post-evaluation for success-degree of power plant technological transformation project based on BPNN[J]. East China Electric Power, 2010, 38(9): 1432–1435.

[17]	Lippmann R P. An introduction to computer with neural nets[J]. IEEE ASSP Magazine, 1987(4): 4–22.

[18]	王小川, 史峰, 郁磊, 等. Matlab神经网络43个案例分析[M]. 北京: 北京航空航天大学出版社, 2013. Wang Xiaochuan, Shi Feng, Yu Lei, et al. Forty three cases analysis of Matlab neural network[M]. Beijing: Beihang University Press, 2013.