文章信息
- 程潜善, 方华亮
- CHENG Qianshan, FANG Hualiang
- 一种应用大数据技术的中长期负荷预测方法
- A prediction method for mid-long term load forecasting using big data technology
- 武汉大学学报(工学版), 2017, 50(2): 239-244
- Engineering Journal of Wuhan University, 2017, 50(2): 239-244
- http://dx.doi.org/10.14188/j.1671-8844.2017-02-013
-
文章历史
- 收稿日期: 2016-03-20
中长期负荷预测是电网规划、建设的基础工作,准确的预测能给电力系统规划部门带来巨大的经济效益.负荷预测本质是基于历史负荷及相关数据推测未来负荷,由于负荷的广域分布和较长的预测年限,负荷受到各种非线性和不确定因素的影响且地域性特点显著,预测难度大.目前对中长期负荷预测的研究重点在预测模型与算法的选择与改进,主要有回归分析法[1]、灰色系统法[2, 3]、证据理论法[4]、神经网络预测法[5]以及支持向量机法[6]等.这些方法主要是对整体负荷的变化趋势进行拟合,基础数据局限于历史负荷序列,较少分析负荷变化的主导因素和地域负荷独特增长规律,其中文献[7]采用互信息理论量化、比较、逐层筛选电力负荷和各影响因素间的互信息,提取二者间的关联规则并依此决策预测;文献[4]提出利用证据理论处理可定量描述的经济产值与难以定量的如政治、气候、政策等不确定因素.
大数据技术[8, 9]源于商业智能,是利用数据分析的方法,从大数据中挖掘有用的信息,进行预测或指导决策.相关文献已提出大数据技术在智能电网[10-12]、负荷影响因素分析[13]等领域的应用.应用大数据技术预测中长期负荷发展,利用其强大的数据处理能力,全面分析类型负荷、区域负荷独特的主导影响因素和变化规律,较好克服整体预测过于粗略缺点,解决负荷预测的类型性特点和地域性特点.本文基于大数据技术体系,提出了大数据技术预测中长期负荷的方法,并通过实例验证了该方法的有效性.
1 大数据技术 1.1 预测模式中长期负荷预测的时间跨度长,会受到众多因素的影响,对应影响因素数据类型多,体量大;负荷广域分布,智能电网观测技术提高以及与电力用户互动的加强,对应负荷数据量也不断扩大.大数据技术是处理这类大体量数据强有力的工具,是一系列处理技术的综合,包括数据采集、数据存储、数据处理以及数据展示等多个环节,特别是数据处理环节的云计算技术,能并行处理大量的数据(图 1).

|
| 图 1 大数据技术预测 Figure 1 Load forecasting using big data technology |
大数据技术解决数据不断丰富的中长期负荷预测问题,重点是利用其强大的数据分析处理技术解决负荷预测内部复杂性.大区域负荷的发展是众多具体负荷发展的综合,通过详细分析具体负荷的变化并加以综合,能准确地预测区域负荷的增长.大数据技术预测负荷,数据质量是关键,中长期负荷预测时间上跨度大,难免存在数据缺失、错误等数据异常,首先应进行预测大数据预处理,对异常数据进行识别和修复[14, 15];然后对预测大数据进行解构,划分成最为具体的负荷集——元负荷,并从多角度分析元负荷的特性,并针对元负荷特性建立对应的预测模型;最后结合解构模式协调大区域负荷增长总量.
1.2 预测分析数据分析是大数据预测的核心.通过对负荷大数据的分析,挖掘出主导负荷变化的影响因素、负荷变化规律以及负荷间复杂关联性等信息,才能进一步建立准确的预测模型.海量数据的分析要依靠大数据技术强大的数据计算能力,如云计算平台(Hadoop)架构和MapReduce模式的组合应用[16].大数据技术与负荷预测数据分析的结合要在合理的模式下进行,如下从负荷分层分区、负荷分类和类型负荷分析3个层次实现对负荷预测大数据的分析.
1.2.1 负荷分层分区预测大数据分布于广域空间,类型多、相互关系复杂.高效地分析这大体量的数据,需构建合理的数据结构体系.结构化数据需通过负荷分层分区来实现.通过将负荷数据分层分区,将大区域负荷预测细化到对应不同地区的预测分区,实现分区独特预测环境精细化的分析与建模.
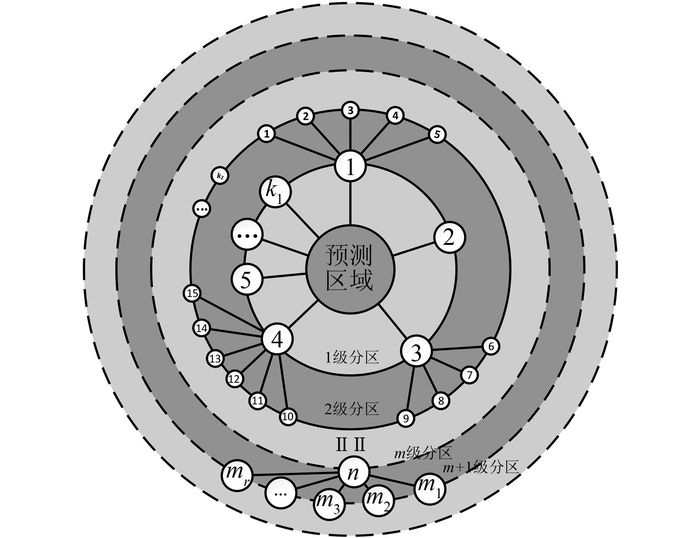
负荷分层分区是针对负荷地域特点,细致分析全局负荷,实现精细化预测的手段.分层分区要与实际负荷分布与管理情况相统一,能反映出负荷地域性的增长规律.同时,负荷分层分区要结合数据收集的便利,要与预测结果最终的规划应用相一致.按照目前电网管理方法,采用与行政区域统一的分层分区方法,从县、市、区(村)、街道等多个层次上划分较为合理.分层具有一定的灵活性,在数据足够充分时,甚至可精确到具体的负荷.分区模型图 2所示.
|
| 图 2 分区模型图 Figure 2 Model of partition |
如图 2所示的预测模型,某一预测分区用Inm表示,其中m是分区级数,对应模型图中同心圆,n指该级具体分区,对应同心圆上的小圆.为表达和存储的方便,对所有m级分区进行编号.根据图 2模型,则有
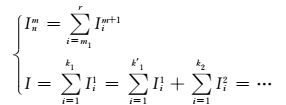 (1)
(1)
式中:r为分区Inm内子分区个数;I表示预测总区域;k1′指无子分区的分区; k1、k2分别表示1级、2级的分区个数.分层分区要与实际统一,要依据数据的详实程度来确定分层级数和分区个数,不同地区可以有不同的级数和区数的划分.
1.2.2 负荷分类不同类型负荷在影响因素和变化规律上有很大的区别,如空调负荷与气温具有相关性且波动幅度大,而重工业负荷量大,但较为稳定.精确预测负荷的增长,必须考虑不同负荷特性的差异.对于各分区,需将不同特性负荷分门别类,针对各类型负荷的特点进行对应的分析和建模.负荷的分类方法视具体情况而定,可从负荷用途的角度或基于负荷曲线所呈现的规律等进行.负荷分类在分区中进行,对于分区Inm,划分为L类型负荷,则有
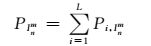 (2)
(2)
通过负荷分层分区、分类,大区域负荷预测化为不同层次细节负荷的预测.针对不同分区特定类型负荷,采用多种数据分析方法,分步挖掘影响负荷变化的主导因素和负荷序列的变化特点等规律.
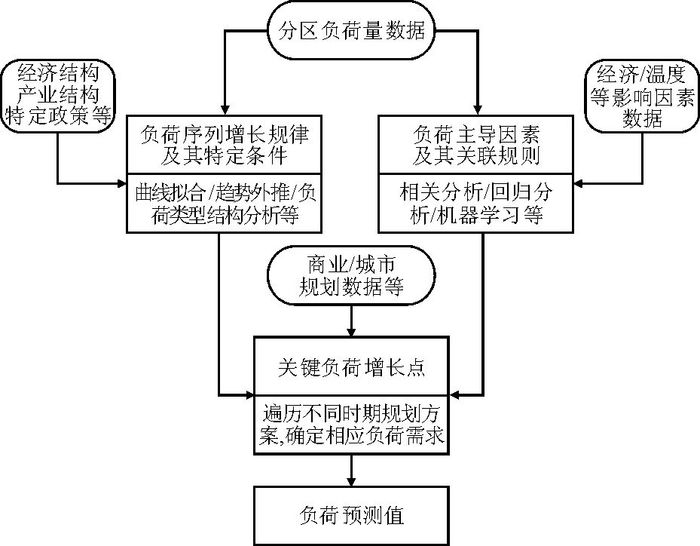
对分区负荷增长特性的分析从2个方面进行,如图 3所示,即结合影响因素数据分析负荷的主导因素及其关联规则;结合地域经济政策特点分析特定条件下的负荷序列增长规律.然后通过遍历各时期规划方案,确定关键负荷增长点,即城市与商业规划中新增的负荷需求.这部分负荷增长是确定性的,可用以修正最终的负荷预测值.
|
| 图 3 负荷增长特性分析 Figure 3 Analysis of load growth characteristics |
传统预测方法基于负荷的统计规律,以负荷总体为对象建立数学模型.大数据预测模型则由数据分析确定,是全局负荷变化规律的综合,反映负荷间复杂关联,是在负荷分类和分层分区基础上的多类型多分区多层次分步修正综合模型.根据建模对象的不同,大数据预测模型分为负荷增长的分析模型与综合模型.
1.3.1 负荷增长分析模型分析模型描述的是各分区类型负荷特有的变化规律.通过分析各分区类型负荷的增长特性,建立相适应的预测模型.各类型负荷模型结构:
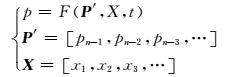 (3)
(3)
式中:p是某分区类型负荷量(用电量);P′是历史负荷序列;X是影响因素向量;x1,x2, x3, …分别表示各量化的影响因素变量,如温度、经济总量等;t为时间.
实际情况中分区类型负荷主导影响因素少,计划性强,负荷增长与城市规划关联密切.模型针对的负荷较为具体,结构相对简单.典型的分析模型主要有规划增长模型、回归分析模型以及指数平滑模型等.
规划增长模型:
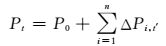 (4)
(4)
式中:Pt为t年后负荷量;P0为基础负荷量;ΔPi, t′为t′年后的负荷规划量.
回归预测模型:
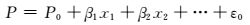 (5)
(5)
式中:x1,x2是影响因素;β1,β2为对应影响系数;ε0为随机变量.
1.3.2 负荷增长综合模型综合模型是统筹分析模型,协调全局负荷,分步实现大区域负荷增长的整合与汇总.在经济发展的特定阶段,各类型负荷间会保持相对稳定的比例关系.类型负荷的独立分析没有计及负荷间彼此的制约关系,同时也易忽略数据错误等原因造成的个别负荷预测结果异常.综合模型通过分步整合分区内的类型负荷与层级中分区负荷,设置合理的修正系数,协调各类型和区域负荷的比例,从而控制全局负荷增量.
Inm+1分区类型负荷增长综合模型:
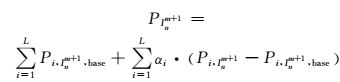 (6)
(6)
式中:Pi, Inm+1, base是依据分区负荷分类模型选取的类型负荷基值; αi是相应类型负荷的修正系数; Pi, Inm+1为类型负荷增长分析模型预测值; PInm+1为分区负荷预测值; L为负荷类型个数.
同理,对于分层级中分区负荷增长综合模型有
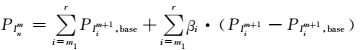 (7)
(7)
式中:PInm为分区负荷预测值; βi为相应子分区修正系数; r为子分区个数.
2 算例分析基于某市的负荷数据和产业经济数据,利用大数据方法体系对该市负荷进行分析预测.依据统计将该市数据分为2层级4分区,全市区域为0级,1级分区依次为A、B、C、D,依次为I11、I21、I31、I41;负荷划分为4种类型,即3大产业用电量和居民生活用电量,依次为W1, Ik1、W2, Ik1、W3, Ik1、W4, Ik1.分区模型与负荷分类模型为
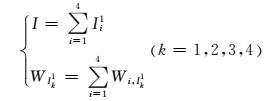 (8)
(8)
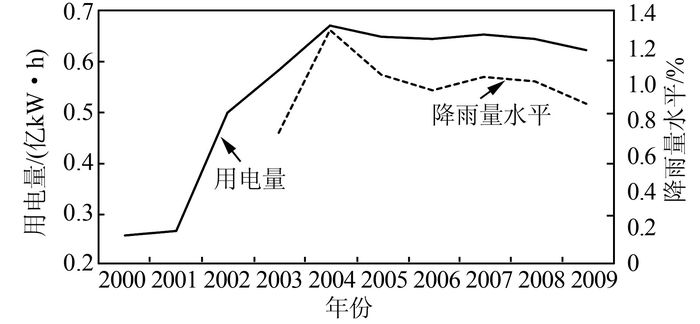
通过分层分区,将数据划分到相应的分区中,依次分析相应类型负荷的变化规律.首先分析A分区数据.对于第1产业用电量W1, I11,主要是农副业用电,经历大发展后农业用电相对饱和,并随着产业结构调整缓慢下降,由图 4可以发现,用电量与降水量呈现出强相关性,建立模型:
|
| 图 4 A区第1产业用电量分析 Figure 4 Analysis of first industrial electricity consumption in section A |
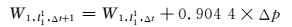 (9)
(9)
其中Δp为与上年的降雨量百分比的差.
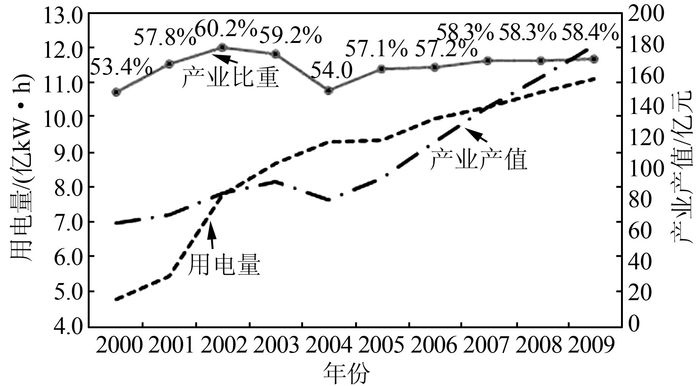
从图 5中看出,第2产业负荷W2, I11的增长与产业产值的增长具有强相关性,增长幅度保持正相关关系.尤其是A区中第2产业产值比例稳定到58%左右后,二者增幅保持为固定的比例.通过产业的调整,第2产业比重会逐步稳定,可以通过增幅比k确定下个时期内的用电量.
|
| 图 5 A区第2产业用电量分析 Figure 5 Analysis of second industrial electricity consumption in section A |
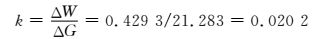 (10)
(10)
根据下1个“5年计划”,每年的经济总量增长约70.2万元,则ΔW=k×ΔG=70.2×0.020 2=1.418,所以2009年之后的用电量为
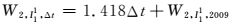 (11)
(11)
第3产业用电W3, I11的时间序列比较特殊,呈波浪线性式增长,奇偶数年份的规律不同.采用最佳平方逼近原则选取拟合公式,通过奇偶数年份的修正系数0.129 5(-1)Δt进一步来精确用电量:
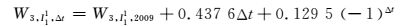 (12)
(12)
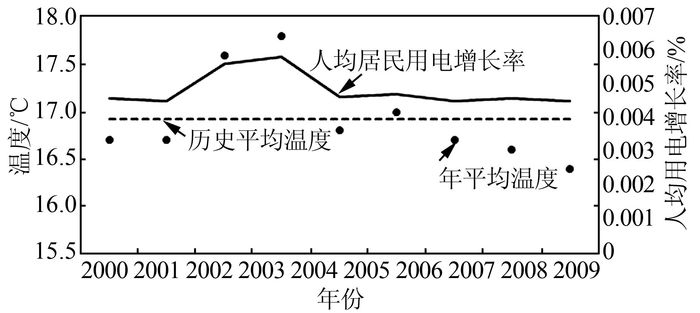
居民生活用电W4, I11所受因素较为复杂,规律性弱.通过图 6的数据分析得知,用电构成上居民生活用电人均用电平稳增加,其中空调负荷比例较大,受气温影响显著,在温度不高于历史均值时,人均居民用电量稳定增长,而高于历史均值时用电量增长率显著提高,建立模型:
|
| 图 6 A区居民生活用电分析 Figure 6 Analysis of residential electricity consumption in section A |
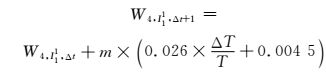 (13)
(13)
式中:m为人口总数;T为历史平均温度;ΔT为当年温度与历史平均温度差.
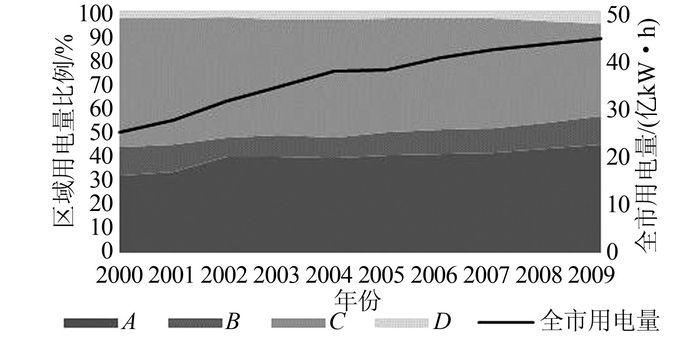
如图 7所示,通过对A地区各类型在全局用电增长中的比例变化的分析,居民生活用电和第1产业用电保持比例不变,第3产业用电以0.2个百分点上升,第2产业以0.2个百分点下降,故对于A分区整体用电量修正公式为
|
| 图 7 全市用电量结构变化图 Figure 7 Change chart of load construction in whole city |
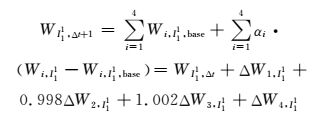 (14)
(14)
分区I21、I31、I41的类型用电和整体用电逐个分析再综合,得出相应分区预测结果.对于整个预测区域内用电量,负荷主要集中在A、C分区中,且A分区占比逐渐上升,D区逐渐减小;B、D分区用电较少,占比稳定.
最终该市的用电量预测结果为
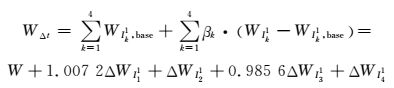 (15)
(15)
全市用电量预测结果如表 1所示.
| GW·h | ||||||
| 区域 | 2010年 | 2011年 | 2012年 | |||
| 预测值 | 实际值 | 预测值 | 实际值 | 预测值 | 实际值 | |
| A区 | 2.280 3 | 2.247 3 | 2.472 3 | 2.488 2 | 2.732 8 | 2.700 8 |
| B区 | 0.593 5 | 0.592 9 | 0.633 6 | 0.631 2 | 0.656 3 | 0.666 7 |
| C区 | 1.970 8 | 1.973 5 | 2.232 5 | 2.211 5 | 2.398 3 | 2.399 2 |
| D区 | 0.260 6 | 0.261 2 | 0.338 3 | 0.337 5 | 0.332 8 | 0.333 4 |
| 全市 | 5.093 3 | 5.074 9 | 5.662 3 | 5.668 3 | 6.105 4 | 6.100 0 |
利用大数据技术分析方法和工具,通过数据分层分区、负荷分类,能够细化分析不同地域负荷、不同类型负荷独特的增长规律;通过负荷结构分析,又能将这些细化分析的负荷合理地综合起来,有效地从元负荷角度预测整体负荷的发展,而且会随着数据收集的逐渐丰富得出更加准确的预测结果.试验算例表明,不同类型负荷各具增长特色,总体预测结果精确度较高.
| [1] |
康重庆, 夏清, 刘梅, 等. 应用于负荷预测中的回归分析的特殊问题[J].
电力系统自动化, 1998, 22(10): 38–41.
Kang Chongqing, Xia Qing, Liu Mei, et al. Special issues of regression analysis in load forecasting[J]. Automation of Electric Power Systems, 1998, 22(10): 38–41. DOI:10.3321/j.issn:1000-1026.1998.10.013 |
| [2] |
张伏生, 刘芳, 赵文彬, 等. 灰色Verhulst模型在中长期负荷预测中的应用[J].
电网技术, 2003, 27(5): 37–40.
Zhang Fusheng, Liu Fang, Zhao Wenbin, et al. Application of grey Verhulst model in middle and long term load forecasting[J]. Power System Technology, 2003, 27(5): 37–40. |
| [3] |
周德强. 改进的灰色Verhulst模型在中长期负荷预测中的应用[J].
电网技术, 2009, 33(18): 124–127.
Zhou Deqiang. Application of improved gray Verhulst model in middle and long term load forecasting[J]. Power System Technology, 2009, 33(18): 124–127. |
| [4] |
倪明, 高晓萍, 单渊达. 证据理论在中期负荷预测中的应用[J].
中国电机工程学报, 1997, 17(3): 199–203.
Ni Ming, Gao Xiaoping, Shan Yuanda. Application of evidential theory in middle-term load forecasting[J]. Proceedings of the CSEE, 1997, 17(3): 199–203. |
| [5] |
李春祥, 牛东晓, 孟丽敏. 基于层次分析法和径向基函数神经网络的中长期负荷预测综合模型[J].
电网技术, 2009, 33(2): 99–104.
Li Chunxiang, Niu Dongxiao, Meng Limin. A comprehensive modelfor long-and medium-term load forecasting based on analytic hierarchy process and radial basis function neural network[J]. Power System Technology, 2009, 33(2): 99–104. |
| [6] |
李瑾, 刘金朋, 王建军. 采用支持向量机和模拟退火算法的中长期负荷预测方法[J].
中国电机工程学报, 2011, 31(16): 63–66.
Li Jin, Liu Jinpeng, Wang Jianjun. Mid-long term load forecasting based on simulated annealing and SVM algorithm[J]. Proceedings of the CSEE, 2011, 31(16): 63–66. |
| [7] |
原媛, 顾洁, 黄薇, 等. 互信息在电力系统中长期负荷预测中的应用[J].
华东电力, 2009, 37(2): 236–239.
Yuan Yuan, Gu Jie, Huang Wei, et al. Application of mutual information to power system medium and long-term load forecasting[J]. East China Electric Power, 2009, 37(2): 236–239. |
| [8] |
孔德智, 刘群兴, 王颖凯, 等. 大数据技术及其应用研究[J].
电子产品可靠性与环境试验, 2013, 31(S1): 90–95.
Kong Dezhi, Liu Qunxing, Wang Yingkai, et al. The research on technology and application of big data[J]. Electronic Product Reliability and Environmental Testing, 2013, 31(S1): 90–95. |
| [9] |
赵刚.
大数据技术与应用实践指南[M]. 北京: 电子工业出版社, 2013: 52-58.
Zhao Gang. Big Data Technology and Applicatice[M]. Beijing: Publishing House of Electronics Industry, 2013: 52-58. |
| [10] |
宋亚奇, 周国亮, 朱永利. 智能电网大数据处理技术现状与挑战[J].
电网技术, 2013, 37(4): 927–935.
Song Yaqi, Zhou Guoliang, Zhu Yongli. Present status and challenges of big data processing in smart grid[J]. Power System Technology, 2013, 37(4): 927–935. |
| [11] |
彭小圣, 邓迪元, 程时杰, 等. 面向智能电网应用的电力大数据关键技术[J].
中国电机工程学报, 2015, 35(3): 503–511.
Peng Xiaosheng, Deng Diyuan, Cheng Shijie, et al. Key technologies of electric power big data and its application prospects in smart grid[J]. Proceedings of the CSEE, 2015, 35(3): 503–511. |
| [12] |
张东霞, 苗新, 刘丽平, 等. 智能电网大数据技术发展研究[J].
中国电机工程学报, 2015, 35(1): 2–12.
Zhang Dongxia, Miao Xin, Liu Liping, et al. Research on development strategy for smart grid big data[J]. Proceedings of the CSEE, 2015, 35(1): 2–12. |
| [13] |
李莉, 栗然. 数据挖掘技术用于负荷与负荷影响因素的相关性分析[J].
华北电力大学学报, 2006, 33(6): 15–19.
Li Li, Li Ran. Relevance analysis of power load and its effects using data mining technology[J]. Journal of North China Electric Power University, 2006, 33(6): 15–19. |
| [14] |
张安珍, 门雪莹, 王宏志, 等. 大数据上基于Hadoop的不一致数据检测与修复算法[J].
计算机科学与探索, 2015, 9(9): 1044–1055.
Zhang Anzhen, Men Xueying, Wang Hongzhi, et al. Hadoop-based inconsistence detection and reparation algorithm for big data[J]. Journal of Frontiers of Computer Science and Technology, 2015, 9(9): 1044–1055. |
| [15] |
曲朝阳, 陈帅, 杨帆, 等. 基于云计算技术的电力大数据预处理属性约简方法[J].
电力系统自动化, 2014, 38(8): 67–71.
Qu Zhaoyang, Chen Shuai, Yang Fan, et al. An attribute reducing method for electric power big data preprocessing based on cloud computing technology[J]. Automation of Electric Power Systems, 2014, 38(8): 67–71. DOI:10.7500/AEPS20130601001 |
| [16] |
张素香, 赵丙镇, 王风雨, 等. 海量数据下的电力负荷短期预测[J].
中国电机工程学报, 2015, 35(1): 37–42.
Zhang Suxiang, Zhao Bingzhen, Wang Fengyu, et al. Short-term power load forecasting based on big data[J]. Proceedings of the CSEE, 2015, 35(1): 37–42. |
 2017, Vol. 50
2017, Vol. 50




