文章信息
- 王洪君, 马冬鹤, 张恩绮, 赵腾飞
- WANG Hongjun, MA Donghe, ZHANG Enqi, ZHAO Tengfei
- 一种无像素膨胀的(3, 3)视觉密码方案
- A (3, 3) visual cryptographic scheme without pixel expansion
- 武汉大学学报(工学版), 2018, 51(12): 1123-1128
- Engineering Journal of Wuhan University, 2018, 51(12): 1123-1128
- http://dx.doi.org/10.14188/j.1671-8844.2018-12-013
-
文章历史
- 收稿日期: 2017-12-02
视觉密码把1幅秘密图像分割成多幅分享图像,多幅或全部分享图像的叠加可以恢复秘密图像,其解密过程不需要复杂的数学计算,只需人的一双眼睛就可实现[1].为了达到信息隐藏的目的,原秘密图像的每个像素无论是黑色还是白色,都被加密成具有固定黑白像素比的多个子像素,所以存在像素膨胀问题.当一定数量的分享图像叠加时,黑色区域具有比白色区域更多的黑色像素,这样秘密信息就可以被识别出来.视觉密码通过把一个像素加密为多个像素达到信息隐藏的目的,这样分享图像往往比秘密图像具有更大的尺寸,研究表明对于一个(k,k)视觉密码方案,理想情况其膨胀度为m=2k-1,即1个像素加密成2k-1个子像素[1].像素膨胀为分享图像的存储和传输带来了不便,为此学者们进行了大量的研究工作,提出了一些解决方案[2-18].
Yang[2]给出一种基于概率的视觉密码方案,利用黑色像素在黑色和白色区域出现概率的不同去区分恢复图像中的黑色和白色区域.例如,对一个(2, 2)的视觉密码方案,恢复后的图像黑色区域仍恢复为黑色,白色区域恢复后只有一半像素为白色,所以能区分黑白区域,该方法恢复的图像和传统的视觉密码方案具有相同的效果.Ito等[3]给出了一个类似于Yang[2]的基于概率的视觉密码方案,加密时随机选择基础矩阵的一列进行分享.Wang等[4]也对Yang[2]的方案进行了改进,得到了更理想的恢复效果.Monoth等[5]也给出了一个基于概率的无像素膨胀秘密分享方案,并进一步对恢复图像的对比度进行了改进[6].Chen等[7]和Kafri等[8]基于随机格给出了3个可视秘密分享算法,在这种方法中首先生成一个称为随机格的分享图像,该图像为一个随机的二值图像,然后另外一个分享图像由秘密图像和随机格产生,这样分享图像和原始秘密图像具有相同的大小.随后有许多基于随机格的视觉密码方案被提出[9-14].Lin等[15]和Chakraborty等[16]分别给出无像素膨胀的秘密图像分享策略,同时对连续的多个像素进行加密.Chakraborty等[16]的方案每次对一个2×2的像素块进行加密,提高了图像加密速度.
针对视觉密码的像素膨胀问题,提出了一种无像素膨胀的(3, 3)视觉密码方案,所给方案产生的分享图像与原始秘密图像具有相同的大小,不存在像素膨胀问题.
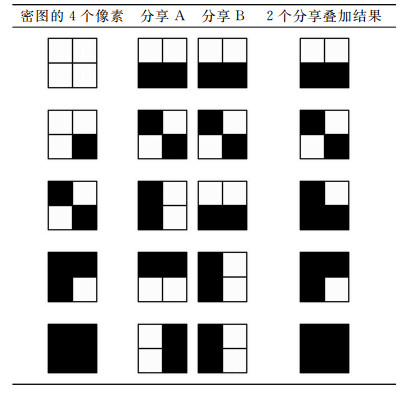
1 相关工作Chakraborty等[16]给出了一个无像素膨胀的(2, 2)视觉密码方案,表 1给出了编码策略.无论原始图像的4个像素颜色如何都被编码成具有2个黑色和2个白色像素的像素块,这样从分享图像中就不能获得秘密图像的信息.图 1给出了所给分享方案的实验结果,当2幅分享图像叠加后,原图像中的黑色像素仍保持黑色,白像素变成灰色.虽然损失了一些对比度,但能够清晰地还原出原始图像的信息.
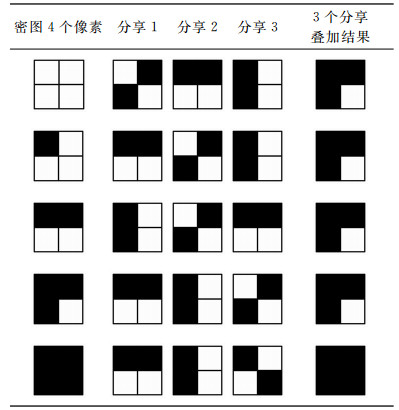
2 无像素膨胀的(3, 3)视觉密码方案 2.1 无像素膨胀的(3, 3)视觉密码方案对Chakraborty等[16]所给分享方案进行扩展,给出一个无像素膨胀的(3,3)视觉密码方案.所给方案分5种情况,如表 2所示.表 2中的黑色方块表示黑色像素,白色方块表示白色像素.
从表 2可以看出,前4行的分享策略中分享叠加结果是相同的,可以用一个基础矩阵来表示,这样所给方案对应的基础矩阵有2个,分别是
 (1)
(1)
其中:数值1表示黑色,数值0表示白色.如果原图像的4个像素至少有一个是白色的,利用基础矩阵S0对其进行分享,如果4个像素都是黑色像素,利用基础矩阵S1对其进行分享.
2.2 秘密图像分享算法所给方案每次处理4个像素,分2行2列,对每个2×2的像素块做如下处理:
步骤1 如果4个像素的颜色都是白色,对S0进行随机的列变换,转步骤6.
步骤2 如果4个像素的颜色为1个黑色和3个白色,选择1个白色像素对应于S0的全0列,其他3列进行列变换,转步骤6.
步骤3 如果4个像素的颜色为2个黑色和2个白色,随机选择1个白色像素对应S0的全0列,其他3列进行随机列变换,转步骤6.
步骤4 如果4个像素的颜色为3个黑色和1个白色,让这个白色像素对应S0的全0列,其他3列进行随机列变换,转步骤6.
步骤5 如果4个像素的颜色都是黑色,对S1进行随机的列变换,转步骤6.
步骤6 分享变换后的基础矩阵的每一行到相应的分享图像.
2.3 实验结果对图 2所示的秘密图像进行实验,实验中所用软件是Matlab 7.0,图像大小为256×256像素,结果如图 3所示.

|
| 图 2 秘密图像 Fig. 2 secret image |

|
| 图 3 所给(3, 3)秘密分享方案实验结果 Fig. 3 Experimental results of proposed (3, 3) visual sharing scheme |
无论原图像的4个像素颜色如何都被加密成2个黑色像素和2个白色像素,分享图像中黑白像素各占50%,使得所产生的分享图像具有相同的像素组成.同时在产生分享图像的过程中,根据2×2像素块的组成情况,对基础矩阵进行相应的随机列变换,使得分享图像中的像素排列是随机的.这种随机性使得分享图像的像素排列杂乱无章,表现为无意义的随机二值图像.正如实验结果所示,分享图像不会暴露秘密图像的任何信息,满足视觉密码的安全性要求[1].另外,由于秘密图像的每个像素加密后的结果只有2个,有可能是黑色像素也可能是白色像素,猜对原始秘密图像像素颜色的概率为2-1,这样对于一个L×H的秘密图像,猜对所有像素的可能性为2-L×H,从单幅分享图像推知秘密图像信息的可能性几乎是不可能的.从分享方案可以看出,任意2幅分享图像的叠加结果是相同的,4个像素中有3个黑色1个白色,所以任何2幅分享图像的叠加也不会暴露原始秘密图像的任何信息.实验结果也证实了这一点.3幅分享图像叠加时,对于秘密图像的白色区域,叠加结果中必含有白色像素,至少有1/4的白色像素仍保持为白色,对于黑色像素叠加结果仍然为黑色像素,黑色区域能完全恢复,所以能够看到原始秘密图像的信息.
2.5 实验结果比较对图 2所示秘密图像用不同的像素不膨胀分享方案进行实验,实验结果如图 4所示.图 4(a)为本文所给方案的实验结果,图 4(b)为基于概率思想的分享方案[2, 3, 17]实验结果,图 4(c)为基于随机格的分享方案[10, 11, 12]的实验结果.从实验结果可以看出本文方案恢复的图像效果最好,基于概率和随机格的分享方案实验结果相当.

|
| 图 4 不同分享方案的实验结果 Fig. 4 Experimental results for various sharing schemes |
PSNR(Peak Signal-to-Noise Ratio)和BER(Bit Error Rate)是衡量恢复图像质量的2个重要指标.PSNR值越大,表明恢复的图像和原始图像越相似;BER值越小,表明恢复的图像和原始图像越接近.利用PSNR和BER对不同分享策略恢复的图像质量进行研究,为此进行了多次实验,实验数据如表 3所示.从表 3中的PSNR值和BER值可以看出,本文所给方案比其他2个方案恢复图像效果要好.同时本方案PSNR值和BER值保持不变,而其他2个方案的这2个值是变的,说明本文所给方案恢复图像效果稳定,而其他2个方案具有随机性.
| 实验次数 | 本文方案 | 基于概率方案 | 基于随机格方案 | |||||
| PSNR | BER | PSNR | BER | PSNR | BER | |||
| 1 | 23.781 3 | 0.370 9 | 23.398 7 | 0.385 4 | 23.378 9 | 0.386 1 | ||
| 2 | 23.781 3 | 0.370 9 | 23.426 1 | 0.384 3 | 23.420 5 | 0.384 5 | ||
| 3 | 23.781 3 | 0.370 9 | 23.466 6 | 0.384 6 | 23.428 4 | 0.384 2 | ||
| 4 | 23.781 3 | 0.370 9 | 23.445 5 | 0.382 8 | 23.477 0 | 0.382 4 | ||
| 5 | 23.781 3 | 0.370 9 | 23.397 5 | 0.385 4 | 23.467 0 | 0.382 7 | ||
| 6 | 23.781 3 | 0.370 9 | 23.419 7 | 0.384 6 | 23.435 6 | 0.383 9 | ||
| 7 | 23.781 3 | 0.370 9 | 23.409 4 | 0.384 9 | 23.433 2 | 0.384 0 | ||
| 8 | 23.781 3 | 0.370 9 | 23.408 2 | 0.385 0 | 23.471 4 | 0.382 6 | ||
| 9 | 23.781 3 | 0.370 9 | 23.458 7 | 0.383 1 | 23.401 5 | 0.385 3 | ||
| 10 | 23.781 3 | 0.370 9 | 23.449 5 | 0.383 4 | 23.413 4 | 0.384 8 | ||
| 平均 | 23.781 3 | 0.370 9 | 23.428 0 | 0.384 4 | 23.432 7 | 0.384 1 | ||
视觉密码的特点是秘密图像的黑色像素能完全恢复,而白色像素只有一部分能恢复,另外一部分转变为黑色像素,所以恢复图像背景颜色变暗.本文也对恢复图像中的白色像素恢复比例进行了实验研究,实验结果表明:本文方案白色像素恢复比例为27.52%(不变),基于概率方案为25%(均值),基于随机格方案为25%(均值).所以本文方案恢复图像更清晰.
3 本文所给视觉密码方案的应用基于本文所给(3, 3)视觉密码方案可以实现身份认证、文本保密和数字水印等.
3.1 身份认证1) 2人共享秘密情况下的身份认证
可信的第3方把秘密图像分割成3个分享图像,自己保持1份留作身份验证时用,另外2个分享图像分发给客户.当客户需要进行身份认证时,客户提供其持有的分享图像,可信的第3方把保存的分享图像和客户的分存图叠加恢复秘密图像,如果恢复出的秘密信息和保存的秘密信息一致,就可以证实客户的身份是真实的.例如,2个合伙人在银行开设1个账户,约定只有2个人都到场的情况下才能取款,那么银行就可以要求2人留下1个用于验证2人身份的秘密信息,银行用这个信息生成3个分享图像,银行自己留下1个分享图像,另外2个分别给2个合伙人,当取款时银行就可以通过叠加分享图像来验证取款人的身份.
2) 网上购物防钓鱼
网上购物,就是通过互联网检索产品信息,并通过网络发出购物申请,然后填写个人支票或信用卡账户号码实现网上支付的一种购物方法.然而一些不法分子会利用虚假网站或邮件骗取受害者的信用卡号、银行账号和密码等信息,即所谓的“钓鱼”.基于本文所提出的(3, 3)视觉密码方案可以防止网上购物中的钓鱼行为.系统由银行服务器、商家和客户3部分构成,商家、客户都在银行服务器上注册了自己的相关信息.当进行交易时,客户首先向商家提供用户名、用户ID等信息,商家把接收到的用户信息连同商家自己的信息发送给银行服务器进行认证.银行首先对商家进行认证,如果认证通过,银行服务器会产生1个一次性密码,并且分割成3幅分享图像,1幅银行自己保留,1幅发送给商家,1幅发送给客户.商家把所收到的分享图像发送给客户,客户收到2份分享图像后,把得到的2个分享图像发回银行服务器.银行服务器利用保留的分享图像和从客户收到的分享图像叠加,恢复一次性密码.如果恢复出的密码是有效的,那么交易继续进行.
3.2 文本保密现实生活中经常要保存一些重要的文本文件,如:财务文件、法律上的契约或证书等.为了保证这些文本文件的安全,或安全地在网上传输这些文件,就可以采用视觉密码来实现.首先将文本转换为黑白二值图像,然后生成分享图像保存起来,不同的分享图像保存在不同的位置,需要恢复这些信息时,分别取出保存的分享图像进行叠加就可以恢复文本文件.如果文本需要通过网络传输到其他地方,那么每一个分享图像可以通过不同的方式发送给接收者(邮件、传真).需要解密时,叠加所有的分享图像就可以恢复原始文本,只有在得到所有分享图像的情况下才能恢复原始数据,否则不能得到原始数据,最后文本就可以通过恢复的图像读出.
3.3 数字水印随着网络技术的发展,数字媒体的传输、分发和访问变得非常方便.然而如何保证数字媒体不被非法使用,保护媒体拥有者的权益不受侵害变得非常重要.数字水印被认为是一种有效的保护版权解决方案.基于本文所给方案可以实现数字水印.水印可以是数字媒体拥有者的签名,签名被转换为二值图像后分割成3幅分享图像:R1,R2和R3,R1嵌入受保护的媒体,R2认证机构保存留作认证时用,R3分发给媒体拥有者.当媒体拥有者提出版权保护时,首先从被嵌入水印的媒体中提取嵌入的分享图像R1,然后与认证机构保存的分享图像R2和申请者拥有的分享图像R3进行叠加,如果得到的叠加结果和申请者的签名一致,那么就证明申请者是媒体的拥有者.另外,媒体拥有者的分享图像R2也可用于验证其身份,首先把媒体拥有者已知的秘密转换为黑白图像S,然后利用基于随机格的秘密分享技术[9],对分享图像R3和秘密图像S进行异或运算得到分享图像S1,S1保存留作身份认证用.当需要认证申请者身份时,对S1和R3进行异或运算,如果恢复出的信息与申请者的秘密一致,申请者的身份就得到了证实.
4 结语针对视觉密码像素膨胀问题进行研究,提出了一个无像素膨胀的(3, 3)视觉密码方案,所产生的分享图像为随机的二值图像,具有与原秘密图像相同的大小.提出的无像素膨胀的秘密分享方案每次处理1个2×2的像素块,提高了秘密图像分享速度.通过实验进一步证实了方案的可行性和有效性.从实验结果和数据分析看,所给方案恢复的图像较基于概率思想的分享方案和基于随机格的分享方案恢复的图像效果更好,恢复图像更清晰.文章最后对本文方案的应用领域进行了探讨.下一步工作将对用户友好的无像素膨胀的视觉密码方案进行研究.
| [1] |
Naor M, Shamir A. Visual cryptography[C]//Advances in Cryptology-Eurocrypt'94, Berlin: Springer-Verlag, 1995, LNCS950: 1-12.
|
| [2] |
Yang C N. New visual secret sharing schemes using probabilistic method[J]. Pattern Recognition Letters, 2004, 25: 481-494. DOI:10.1016/j.patrec.2003.12.011 |
| [3] |
Ito R, Kuwakado H, Tanaka H. Image size invariant visual cryptography[J]. IEICE Trans Fundamentals, 1999, E82-A(10): 2172-2177. |
| [4] |
Wang D, Zhang L, Ma N, et al. Two secret sharing schemes based on boolean operations[J]. Pattern Recognition Letters, 2007, 40(10): 2776-2785. DOI:10.1016/j.patcog.2006.11.018 |
| [5] |
Monoth T, Anto B P. Recursive visual cryptography using random basis column pixel expansion[C]//Proceedings of the IEEE International Conference on Information Technology 2007, California: IEEE Computer Society Press, 2007: 41-43.
|
| [6] |
Monoth T, Anto B P. Achieving optimal contrast in visual cryptography schemes without pixel expansion[J]. International Journal of Recent Trends in Engineering, 2009, 1(1): 468-471. |
| [7] |
Chen T H, Tsao K H. Visual secret sharing by random grids revisited[J]. Pattern Recognition, 2009, 42(9): 2203-2217. DOI:10.1016/j.patcog.2008.11.015 |
| [8] |
Kafri O, Keren E. Encryption of pictures and shapes by random grids[J]. Optics Letters, 1987, 12(6): 377-379. DOI:10.1364/OL.12.000377 |
| [9] |
Shyu S J. Image encryption by random grids[J]. Pattern Recognition, 2007, 40(3): 1014-1031. DOI:10.1016/j.patcog.2006.02.025 |
| [10] |
Shyu S J. Image encryption by multiple random grids[J]. Pattern Recognition, 2009, 42(7): 1582-1596. DOI:10.1016/j.patcog.2008.08.023 |
| [11] |
Chen T H, Tsao K H. Threshold visual secret sharing by random grids[J]. Journal of Systems and Software, 2011, 84(7): 1197-1208. DOI:10.1016/j.jss.2011.02.023 |
| [12] |
Chen T H, Tsao K H. User-friendly random grid-based visual secret sharing[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2011, 21(11): 1693-1703. DOI:10.1109/TCSVT.2011.2133470 |
| [13] |
Paknahad S M, Hosseini S A, Alaghband M R. User-friendly visual secret sharing based on random grids[C]//Signal Processing and Intelligent Systems Conference, IEEE, 2015: 58-62.
|
| [14] |
Liu C L, Tsai W J, Chang T Y, et al. Meaningful share generation for (2, 2)-multiple visual secret sharing scheme without pixel expansion[J]. Computer Journal, 2015, 58(7): 1598-1606. DOI:10.1093/comjnl/bxu105 |
| [15] |
Lin T L, Horng S J, Lee K H, et al. A novel visual secret sharing scheme for multiple secrets without pixel expansion[J]. Expert Systems with Applications, 2010, 37: 7828-7869. |
| [16] |
Chakraborty U, Paul J K, Mahapatera P R S. Design and implementation of a (2, 2) and a (2, 3) visual cryptographic scheme[J/OL]. (2012-4-18)[2013-7-20]. http://interscience.in/SpIss_ijcct_accta_2010vol1_nol2/CS_Paper2.pdf.
|
| [17] |
候永昌, 官振宇, 蔡志丰, 等. 没有形变的(3, n)-视觉秘密分享方案[J]. 计算机学报, 2016, 39(3): 441-453. Hou Yungchang, Quan Zenyu, Tsai Zhinfong. (3, n)-visual secret sharing scheme with unexpanded shares[J]. Chinese Journal of Computers, 2016, 39(3): 441-453. |
| [18] |
胡浩, 郁滨, 沈刚. 像素不扩展视觉密码的边缘增强研究[J]. 计算机科学, 2015, 42(2): 103-107. Hu Hao, Yu Bin, Shen Gang. Edge enhancement on size invariant visual cryptography[J]. Computer Science, 2015, 42(2): 103-107. |
 2018, Vol. 51
2018, Vol. 51