文章信息
- 唐科, 文武, 阮江军, 詹清华, 肖微, 刘超
- TANG Ke, WEN Wu, RUAN Jiangjun, ZHAN Qinghua, XIAO Wei, LIU Chao
- 基于有限元法的单芯电缆温度场仿真研究
- Temperature field simulation of single core cable based on FEM
- 武汉大学学报(工学版), 2018, 51(9): 811-816
- Engineering Journal of Wuhan University, 2018, 51(9): 811-816
- http://dx.doi.org/10.14188/j.1671-8844.2018-09-010
-
文章历史
- 收稿日期: 2017-10-25
2. 广东电网公司佛山供电局,广东 佛山 52800
2. Foshan Power Supply Bureau, Guangdong Power Grid, Foshan 528000, China
电力电缆是电力系统中不可或缺的重要组成部分,承担着电能传输的重任[1, 2].随着电力系统的发展,电缆的电压等级和输送能量持续增加,电缆运行时温升向极限温度接近.而温度是反映电缆运行状态十分重要的参数,电缆的绝缘老化程度与温度密切相关,当电缆处在非正常的过热状态,会加速电缆的绝缘老化,甚至会发生热击穿,对输电线路安全稳定运行构成了威胁.研究发现,当交联聚乙烯(XLPE)电缆的工作温度超过长期允许最高工作温度的8%时,其寿命将会减半;工作温度超过长期允许最高工作温度的15%时,电缆寿命将只剩下原来的1/4[3-6].
目前,国内外对电缆温度的计算主要有2种方法:热路法和数值计算方法.热路法的代表是IEC-60287IEC-60853,将实际模型简化为一维,然后再进行计算,计算结果存在一定的误差[7-9].随着复杂条件下密集排列电力电缆群的出现,电缆间的电磁-热的相互作用更加强烈,其损耗和散热计算往往和多种因素有关,因而不能简单按标准给定的方法进行分析[10].为了尽可能准确地模拟电缆埋设区域的温度场,必须借助数值方法,在给定敷设条件和环境条件以及电缆参数的前提下,用温度场分布来分析电缆周围的温度情况.目前常用的数值计算方法有边界元法、有限差分法、有限容积法以及有限元法等[11-13].
电缆接头是电缆安全运行的薄弱环节,准确了解电缆接头的温度情况,对电力系统的安全稳定运行具有重要意义.
本文对直埋式水平排列单芯电缆的温度场、三相电缆温度场之间的关系进行了分析.对110 kV直埋式单芯电缆,采用有限元软件Ansys分别仿真了单根电缆和三相电缆的温度场,通过对比分析后,提出了建立二者温度差和电流的函数来表征二者的温度差异,仿真得到单根电缆的温度情况,代入所获得的拟合函数就能得到三相电缆的温度情况.并将该方法应用到电缆接头的温度场仿真中,使其仿真结果更加准确.
1 电缆有限元模型的建立 1.1 电缆敷设模型的建立对于实际的电缆,经过合理简化后,分为5层,从内到外依次为缆芯、绝缘层、防水层、皱纹铝护套和外护套,如图 1所示.

|
| 图 1 单芯电缆横截面结构模型 Fig. 1 Cross section structure model of single core cable |
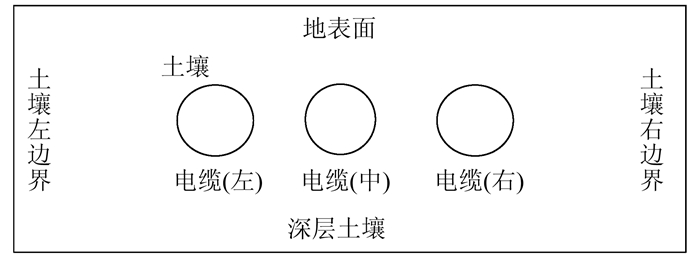
根据电力电缆敷设的相关标准[14, 15],建立直埋式电缆的温度场模型,电缆水平敷设,距地表 0.8 m,电缆间距为0.4 m,如图 2所示.
|
| 图 2 电缆敷设简易示意图 Fig. 2 Simple diagram of cable laying |
土壤的边界条件可以由传热学中的3类边界条件确定[11].
第1类边界条件是已知边界温度函数,可表示为
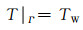 (1)
(1)
式中:Г为积分边界;TW为已知温度边界,℃.土壤下边界属于第1类边界条件,深层土壤温度TW跟土壤深度有关,一般取25 ℃.
第2类边界条件是已知边界法向热流密度,表示为
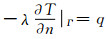 (2)
(2)
式中:λ为导热系数,W/(m·℃);q为已知热流密度,W/m2.电缆水平方向温度梯度为0,因此土壤左右边界属于第2类边界.
第3类边界条件是对流边界条件,即已知对流换流系数和流体温度,表示为
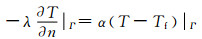 (3)
(3)
式中:α为对流换热系数,W/(m2·℃);Tf为流体温度,℃.地表为第3类边界条件,在仿真中选择空气温度为35 ℃,对流交换系数为8 W/(m2·℃).
在电缆附近的土壤温度变化较为剧烈,远离电缆的土壤温度变化不大,通常距离电缆2 000 mm的土壤已不受电缆的影响[1],通过计算后,最终选择左右边界取距电缆4 000 mm的直线.
1.3 损耗计算整个温度场的热源包括电缆的导体损耗、介质损耗、金属护套损耗等,这些参数可以根据IEC-60287标准进行计算[16-18].
当电流流过电缆时,电缆缆芯导体发热,根据欧姆定律,并忽略电缆导体中的热量损失,可得单位长度电缆线芯发热量为S=I2R.
单位长度线芯的有效电阻R一般可由下式计算:
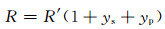 (4)
(4)
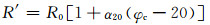 (5)
(5)
式中:R0为单位长度电缆线芯在20 ℃时的直流电阻, Ω/m;φc为线芯温度,℃;R′为单位长度线芯在φc时的直流电阻,Ω/m;ys为集肤效应系数;yp为临近效应系数;α20为线芯导体材料以20 ℃为基准时的电阻温度系数,1/℃.
当所计算的电缆电压等级较高时,绝缘层介质损耗不可忽略.单位长度电缆绝缘层的介质损耗为
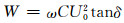 (6)
(6)
式中:ω =2πf, rad/s;tanδ为工频下的绝缘损耗因数;U0为电缆绝缘层承受的电压, V;C为单位长度电缆的电容, F/m.
金属护套损耗包括环流损耗与涡流损耗.当电缆导体通过工频交流电流时,在其周围产生工频电磁场,电缆外层的金属护套将产生涡流损耗;当电缆金属套双端接地时,由于每相金属套间产生的电磁感应电势不相等,金属护套中将产生环流损耗[19].
2 电缆温度场仿真 2.1 土壤下边界的选择虽然通常距离电缆2.0 m的土壤不受电缆影响,但不能确定2.0 m是否是最合适的土壤下边界.为了选择一个合适的下边界,研究在缆芯电流为1 300 A不同土壤深度时的电缆缆芯温度情况,不同土壤深度下电缆缆芯的温度变化如表 1所示,其中三相电缆以左右两根为例.
| 缆芯距下边界的距离/m | 缆芯温度/℃ | |
| 单根 | 三相(左右) | |
| 0.8 | 71.636 | 80.348 |
| 2.4 | 74.972 | 87.749 |
| 3.2 | 75.804 | 89.146 |
| 4.0 | 76.344 | 90.030 |
通过对不同土壤深度电缆缆芯的温度进行对比,可以发现在电缆中心距土壤下边界为4.0 m以后,继续加大下边界深度,电缆缆芯处的温度变化不大,所以最终选择距缆芯4.0 m处作为土壤下边界.
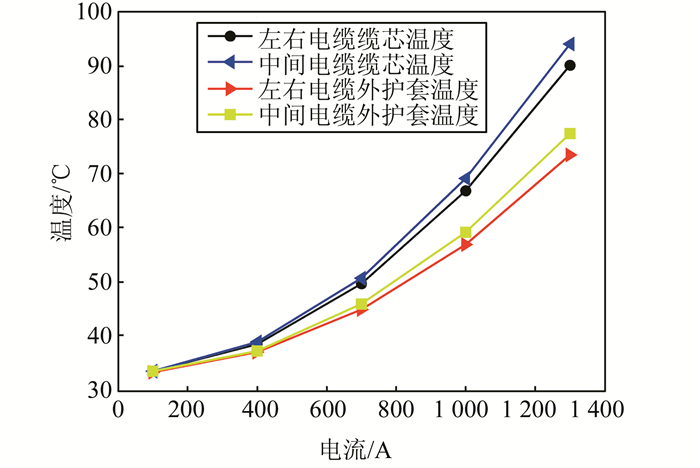
2.2 三相电缆的温度场仿真加载3类边界条件,即土壤下边界为温度边界,土壤左右边界为法向热流密度边界,地表面为对流边界,对不同缆芯电流下三相电缆进行温度场仿真.对于水平敷设的三相电缆,左右两根电缆的温度情况与中间电缆并不相同,分别分析其温度情况.以电缆缆芯温度和外护套温度作为分析对象,不同电流情况下,电缆的温度情况如图 3所示.700 A时三相电缆的温度分布如图 4所示.
|
| 图 3 三相电缆不同电流仿真温度 Fig. 3 Three-phase cable simulation temperature under different current |
|
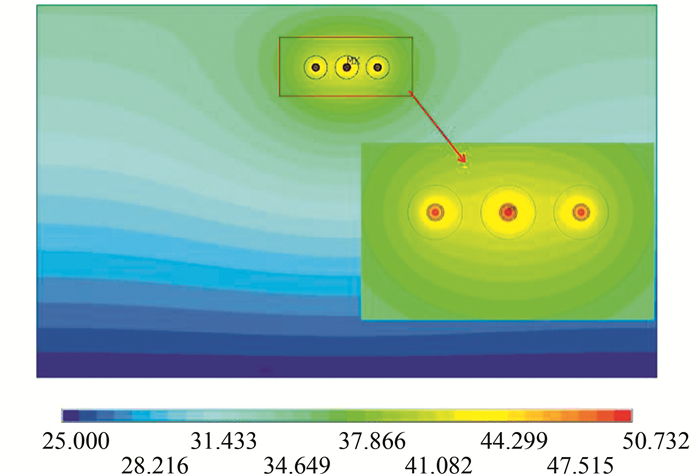
| 图 4 700 A时三相电缆的温度分布(单位:℃) Fig. 4 Temperature distribution of three-phase cable in 700A (unit:℃) |
由图 3、4可以发现,受邻近电缆温度的影响,三相电缆水平敷设时,中间电缆的温度最高,温度最高点出现在缆芯处,温度沿电缆径向依次降低;随着缆芯电流的增加,缆芯温度和外护套温度随之增加,缆芯和外护套之间的温度差异也随之增加;同一电流下,中间电缆与左右电缆缆芯之间的温度差和外护套之间温度差基本一致.
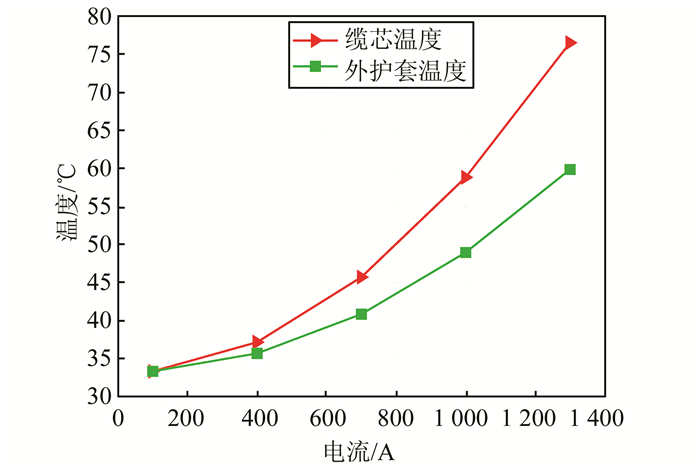
2.3 单根电缆的温度场仿真同样,为了研究单根电缆(取中间电缆位置)的温度情况,在不同缆芯电流下进行温度场仿真,加载与三相电缆相同的边界条件,得到不同电流情况下,电缆温度的情况如图 5所示.700 A时单根电缆的温度分布如图 6所示.在单根电缆时,只有一个电缆热源,而在三相电缆时,有3个电缆热源,三相电缆通过热传导温度相互影响,使得温度高于单根电缆.
|
| 图 5 单根电缆不同电流仿真温度 Fig. 5 Single cable simulation temperature under different current |
|
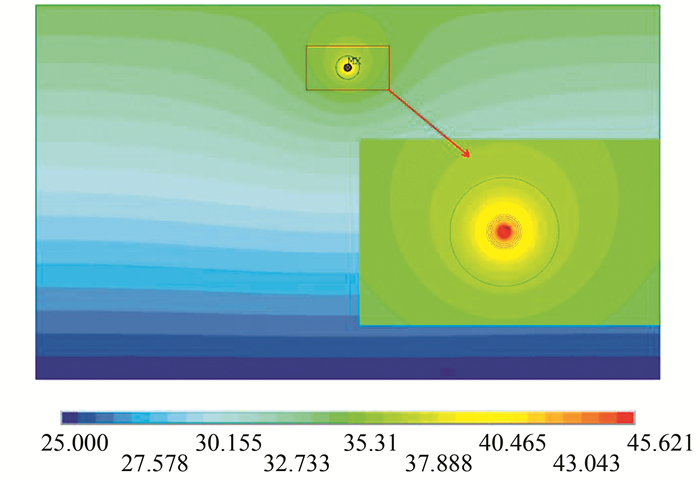
| 图 6 700 A时单根电缆的温度分布(单位:℃) Fig. 6 Temperature distribution of single cable in 700 A (unit:℃) |
由图 5、6可以发现,与三相电缆一样,缆芯温度和外护套温度随着电流的增加而增加,缆芯和外护套之间的温度差异也随之增加;与三相电缆相比,在同一电流下,单根电缆的温度低于三相电缆的温度.
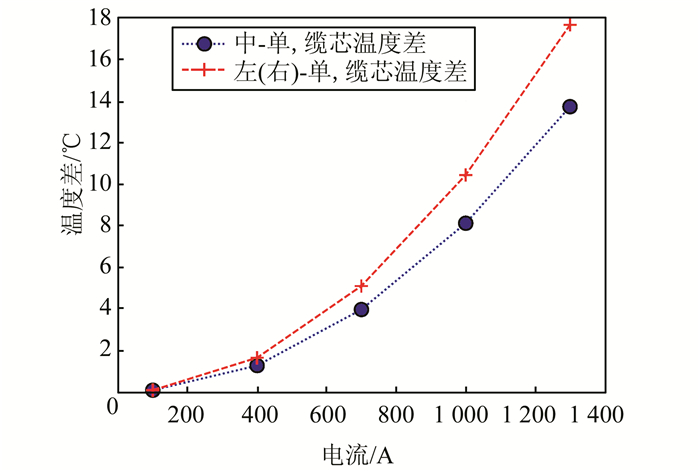
3 电缆温度差异分析 3.1 缆芯温度差异分析将第2节2种情况仿真所得到的缆芯温度汇总,将缆芯温度差作为纵坐标,缆芯电流作为横坐标,得到温度差异散点图如图 7所示,可以看出温度差与电流大致呈幂次方走向,其中将三相电缆中中间电缆和中间电缆单独分析.
|
| 图 7 缆芯温度差异散点图 Fig. 7 Temperature difference scatter diagram of cable core |
如果想通过仿真单根电缆的温度得到三相电缆的温度情况,可以建立温度差和电流的函数.在Matlab中,拟合温度差和电流的函数,选择的拟合函数为幂指数函数f(x)=axb+c,由拟合结果发现,2个拟合函数的系数b分别为2.002和2.001,所以最终选择选择二次函数y=ax2+bx+c进行拟合.分析其原因,电缆最主要热源是缆芯发热,而缆芯热源为S=I2R,故缆芯的热源与缆芯电流的二次幂成正比,所以可以认为缆芯的温升与缆芯电流的二次幂成正比,故可以得到三相电缆与单根电缆的温度差与缆芯电流的二次幂成正比.
利用单根电缆来研究三相电缆中的左右电缆,可以利用函数得到:
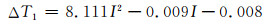
利用单根电缆来研究三相电缆中的中间电缆,可以利用函数得到:
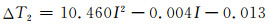
其中:I表示缆芯电流,kA;ΔT表示与I对应的温度差,℃.
3.2 外护套温度差异分析单根电缆和三相电缆的外护套温度差异与缆芯温度差异一致,如表 2所示.
| 电流/A | 左(右)-单 | 中-单 | |||
| 缆芯温度差/℃ | 外护套温度差/℃ | 缆芯温度差/℃ | 外护套温度差/℃ | ||
| 100 | 0.07 | 0.07 | 0.09 | 0.09 | |
| 400 | 1.29 | 1.29 | 1.66 | 1.66 | |
| 700 | 3.96 | 3.97 | 5.11 | 5.11 | |
| 1 000 | 8.09 | 8.11 | 10.44 | 10.42 | |
| 1 300 | 13.69 | 13.71 | 17.66 | 17.63 | |
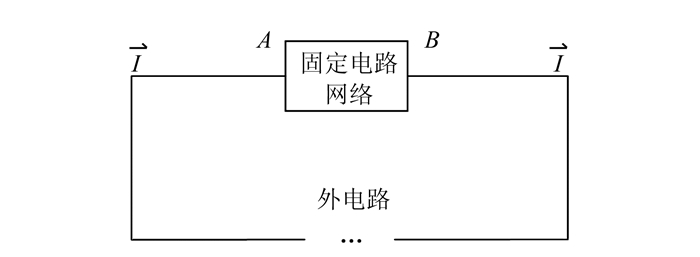
对于单根电缆和三相电缆,在同一电流下,电缆缆芯温度与外护套温度差为一个定值,即外护套温度为缆芯温度减掉相同温度值,所以,在同一电流下二者外护套温度差异与缆芯温度差异一致.可以类比电路的情况,如图 8所示,在电流一定的情况下,如果节点A到节点B所包含的电路结构完全相同,可以把A、B节点所包含的网络看做一个整体,无论A、B节点外电路情况如何,A、B节点的电压差为一定值.对于热路而言,电压差即温度差,固定电路网络即电缆缆芯至外护套结构参数完全一样,而外电路不同即电缆根数不同.
|
| 图 8 类比电路分析原理图 Fig. 8 Schematic diagram of analog circuit analysis |
不仅是外护套,其他各层的温度都可以代入上面的拟合函数得到,因为对于单根电缆和三相电缆,从缆芯到其他各层的参数一致,同一电流下缆芯与其他层的温度差为一定值,这样对于单、3根电缆的其他层的温度差异也与缆芯差异一致.仿真单根电缆的温度场,代入拟合函数求出温度差,就可得到三相电缆的温度场.
可以验证其他电流下,计算得到的温度差与仿真得到的温度差一致,以缆芯电流为630 A为例,分别对单根电缆和三相电缆进行温度场仿真,得到电缆的温度情况如表 3所示.
| 位置 | 温度/℃ | 温度差/℃ | ||||
| 单根 | 左(右) | 中 | 右-单 | 中-单 | ||
| 缆芯 | 43.24 | 46.44 | 47.38 | 3.20 | 4.14 | |
| 外护套 | 39.34 | 42.55 | 43.47 | 3.21 | 4.13 | |
将电流I=0.63 kA代入温度函数:
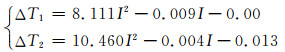
计算得
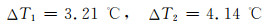
与表 3中单、3根电缆温度差异一致,可见,用所求得的拟合函数来计算温度差效果很好.
4 电缆接头温度场仿真采用文献[20]的电缆接头模型,缆芯电流仍然为1 000 A.由文献[20]可知,电缆接头土壤外半径为1.0 m,可以模拟埋深为0.8 m的实际土壤电缆,此时,电缆接头最高温度为85.85 ℃.
为考虑三相电缆水平敷设时电缆接头的温度情况,采用上面的方法来修正电缆接头的温度,将I= 1.0 kA代入函数:
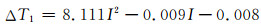
得ΔT1=8.09 ℃,将I=1.0 kA代入函数:
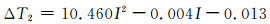
得ΔT2=10.44 ℃.可以得到,修正后三相电缆中左右电缆接头最高点温度为93.94 ℃,三相电缆中中间电缆接头最高点温度为96.29 ℃.
在未进行温度修正时,电缆接头最高温度为85.85 ℃,而修正后电缆接头最高温度为93.94 ℃(左右)和96.29 ℃(中),修正前后电缆接头温度差异较大.而对于交联聚乙烯电缆,导体能够长期工作的温度是90 ℃.在温度修正前,电缆接头最高温度并没有达到90 ℃,但是修正后电缆接头最高温度已经超90 ℃,如果采用未修正前的温度来确定电缆的载流量,会使缆芯温度过高,加速电缆绝缘的老化,减少电缆的使用寿命,因此,温度修正对分析电缆接头的温度情况意义重大.
5 结论采用有限元法分别仿真了单根电缆和三相电缆的温度场,通过对比分析后,提出了建立二者温度差和电流的函数来计算二者的温度差异,结果表明,温度差和电流呈现良好的二次函数关系.同时,电缆各层的温度差异都可以用同一拟合函数计算得到.通过本文提出的方法,仅通过仿真单根电缆的温度场即可知三相电缆的温度情况,大大减少了仿真的计算量和计算时间.
将温度差异修正方法应用到电缆接头的温度场仿真中,可以看出温度修正的重要意义.
| [1] |
张洪麟, 唐军, 陈伟根, 等. 基于有限元法的地下电缆群温度场及载流量的仿真计算[J]. 高压电器, 2010, 46(2): 42-51. Zhang Honglin, Tang Jun, Chen Weigen, et al. Simulation of temperature field and ampacity of underground cable system based on finite element method[J]. High Voltage Apparatus, 2010, 46(2): 42-51. |
| [2] |
徐元哲, 王乐天, 刘冬雪, 等. 电力电缆接头测温系统的设计[J]. 高电压技术, 2009, 35(12): 2977-2982. Xu Yuanzhe, Wang Letian, Liu Dongxue, et al. Design of temperature measurement system for power cable junction based on FBG[J]. High Voltage Engineering, 2009, 35(12): 2977-2982. |
| [3] |
杨文英.电力电缆温度在线监测系统的研究[D].吉林: 东北电力大学, 2008. Yang Wenying. Studying on the on-line temperature monitoring system for power cable[D]. Jilin: Northeast Dianli University, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10188-2008051952.htm |
| [4] |
杨延明.基于有限元法的电力电缆载流量计算[D].哈尔滨: 哈尔滨理工大学, 2012. Yang Yanming. Power cable ampacity calculation based on finite element method[D]. Harbin: Harbin University of Science and Technology, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10214-1013173685.htm |
| [5] |
珞灵琳.电缆暂态温度场及载流量实时计算方法的研究[D].重庆: 重庆大学, 2008. Luo Linglin. Study on the transient-state temperature field and ampacity real-time caculation method of single core cable[D]. Chongqing: Chongqing University, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10611-2009046883.htm |
| [6] |
王有元, 陈仁刚, 陈伟根, 等. 有限元法计算地下电缆稳态温度场及其影响因素[J]. 高电压技术, 2009, 35(12): 3086-3092. Wang Youyuan, Chen Rengang, Chen Weigen, et al. Calculation of static temperature field of buried cable based on FEM and analysis of influential factors[J]. High Voltage Engineering, 2009, 35(12): 3086-3092. |
| [7] |
梁永春, 李延沐, 李彦明, 等. 利用模拟热荷法计算地下电缆稳态温度场[J]. 中国电机工程学报, 2008, 28(16): 129-134. Liang Yongchun, Li Yanmu, Li Yanming, et al. Calculation of the static temperature field of underground cables using heat charge simulation method[J]. Proceedings of the CSEE, 2008, 28(16): 129-134. DOI:10.3321/j.issn:0258-8013.2008.16.021 |
| [8] |
刘刚, 雷成华, 刘毅刚. 根据电缆表面温度推算导体温度的热路简化模型暂态误差分析[J]. 电网技术, 2011, 35(4): 212-217. Liu Gang, Lei Chenghua, Liu Yigang. Analysis on transient error of simplified thermal circuit model for calculating conductor temperature by cable surface temperature[J]. Power System Technology, 2011, 35(4): 212-217. |
| [9] |
马国栋. 电线电缆载流量[M]. 北京: 中国电力出版社, 2013. Ma Guodong. Capacity of Transmission Line and Cables[M]. Beijing: China Electric Power Press, 2013. |
| [10] |
梁永春. 高压电力电缆载流量数值计算[M]. 北京: 国防工业出版社, 2012. Liang Yongchun. Numercial Calculation of High Voltage Power Cable Capacity[M]. Beijing: National Defence Industry Presss, 2012. |
| [11] |
徐妍, 王丽娜, 李艳飞. 电缆温度场的有限元分析[J]. 黑龙江电力, 2011, 33(1): 31-36. Xu Yan, Wang Lina, Li Yanfei. Analysis of temperature field of the cable based on FEM[J]. Heilongjiang Electric Power, 2011, 33(1): 31-36. DOI:10.3969/j.issn.1002-1663.2011.01.009 |
| [12] |
于建立, 常树生, 牛远方, 等. 地下电力电缆温度场及载流量的数值计算[J]. 东北电力大学学报, 2008, 28(4): 62-65. Yu Jianli, Chang Shusheng, Niu Yuanfang, et al. Numerical simulation of thermal fields and ampacity of underground power cables[J]. Journal of Northeast Dianli University, 2008, 28(4): 62-65. DOI:10.3969/j.issn.1005-2992.2008.04.013 |
| [13] |
周晓虎, 周秧, 唐雷, 等. 直埋电力电缆温度场计算模型[J]. 电线电缆, 2007(5): 33-36. Zhou Xiaohu, Zhou Yang, Tang Lei, et al. Mathematical model for calculation of the temperature profile in buried power cables[J]. Electric Wire & Cable, 2007(5): 33-36. DOI:10.3969/j.issn.1672-6901.2007.05.009 |
| [14] |
GB 50217-2007电力工程电缆设计规范[S].北京: 中国计划出版社, 2007. GB 50217-2007 Code for Design of Cables of Electric Engineering[S]. Beijing: Chins Planning Press, 2007. |
| [15] |
DL/T 5221-2005城市电力电缆线路设计技术规定[S].北京: 中国电力出版社, 2005. DL/T 5221-2005 Technical Code for the Design of Urban Power Cables[S]. Beijing: China Electric Power Press, 2005. |
| [16] |
IEC60287-1 Calculation of the Current Rating, Part 1: Current Rating Equations(100% Load Factor)and Calculation of Losses[S], 2001.
|
| [17] |
IEC60287-2 Calculation of the Current Rating, Part 2: Thermal Resistance[S], 2001.
|
| [18] |
IEC60287-3 Calculation of the Current Rating, Part 3: Sections on Operating Conditions[S], 1999.
|
| [19] |
梁永春, 柴进爱, 李彦明, 等. 有限元法计算交联电缆涡流损耗[J]. 高电压技术, 2007, 33(9): 196-199. Liang Yongchun, Cai Jinai, Li Yanming, et al. Calculation of eddy current losses in XLPE cables by FEM[J]. High Voltage Engineering, 2007, 33(9): 196-199. DOI:10.3969/j.issn.1003-6520.2007.09.044 |
| [20] |
唐科, 文武, 丁俊杰, 等. 基于有限元法的电缆接头温度场仿真[J]. 电力建设, 2016, 37(2): 145-150. Tang Ke, Wen Wu, Ding Junjie, et al. Temperature field simulation of cable joints based on FEM[J]. Electric Power Construction, 2016, 37(2): 145-150. DOI:10.3969/j.issn.1000-7229.2016.02.021 |
 2018, Vol. 51
2018, Vol. 51




