武汉大学学报(工学版)   2016, Vol. 49 Issue (2): 247-253

文章信息

杨国俊, 李子青, 郝宪武, 王晓明, 宋涛
YANG Guojun, LI Ziqing, HAO Xianwu, WANG Xiaoming, SONG Tao
非对称悬索桥对称竖弯基频的实用计算公式
Practical Fundamental Frequency Formulas for Symmetric Vertical Vibration of Asymmetry Suspension Bridge
武汉大学学报(工学版), 2016, 49(2): 247-253
Engineering Journal of Wuhan University, 2016, 49(2): 247-253
http://dx.doi.org/10.14188/j.1671-8844.2016-02-015

文章历史

收稿日期: 2015-06-25
 Abstract              PDF               Figures               Tables
引用本文 0
杨国俊, 李子青, 郝宪武, 王晓明, 宋涛. 非对称悬索桥对称竖弯基频的实用计算公式[J]. 武汉大学学报(工学版), 2016, 49(2): 247-253.
YANG Guojun, LI Ziqing, HAO Xianwu, WANG Xiaoming, SONG Tao. Practical Fundamental Frequency Formulas for Symmetric Vertical Vibration of Asymmetry Suspension Bridge[J]. Engineering Journal of Wuhan University, 2016, 49(2): 247-253.
非对称悬索桥对称竖弯基频的实用计算公式
杨国俊, 李子青, 郝宪武, 王晓明, 宋涛     
长安大学公路学院，陕西 西安 710064
收稿日期: 2015-06-25
作者简介: 杨国俊（1988-）男，博士研究生，主要从事桥梁结构及结构分析理论，E-mail:798602505@qq.com.
通讯作者: 李子青（1954-）男，教授，博士生导师，主要从事桥梁结构及结构分析理论，E-E-mail:hxw@126.com.
基金项目: 教育部高校博士新教师基金（编号:20130205120001）;中央高校基本科研业务费资助项目（编号:2013G1211010）.
摘要: 为了方便计算非对称悬索桥的对称竖弯自振基频，采用Rayleigh法分别推导了不考虑和考虑边缆和主塔刚 度影响下的非对称悬索桥一阶对称竖弯自振基频的近似计算公式，提出了修正规范公式的非对称结构参数影响因 子和计入边缆和主塔刚度的非对称结构参数影响因子，并给出了边缆和主塔刚度对竖向自振基频的影响系数的表 达式，最后通过有限元法验证近似公式的精度。研究结果表明:在计算非对称悬索桥竖向自振基频时不能忽略边缆 和主塔刚度的影响，计入边缆和主塔刚度影响的实用公式计算结果与有限元法计算结果非常接近，误差为3.3%, 能满足工程上对精度的要求，可以方便指导非对称悬索桥的方案选择和初步设计。
关键词： 桥梁工程     非对称悬索桥     基频     瑞利法     主塔刚度    
Practical Fundamental Frequency Formulas for Symmetric Vertical Vibration of Asymmetry Suspension Bridge
YANG Guojun, LI Ziqing, HAO Xianwu, WANG Xiaoming, SONG Tao     
School of Highway, Chang’an University, Xi’an710064, Shaanxi,China
Abstract: In order to calculate symmetric vertical vibration frequencies of asymmetry suspension bridge conveniently, frequency formulas for 1st symmetric vertical vibration of asymmetry suspension bridge were derived under both cases that considering and not considering the influence of side-cable and tower stiffness on vibration frequencies based on Rayleigh，s method. Asymmetric structure influencing factors in revised standard formulas and that considering the influence of side-cable and tower stiffness were both put forward. Formula for influencing factors of side-cable and tower stiffness on vibration frequency was also given. Finally, the result under finite element method was taken to examine the accuracy of proposed formulas. The results indicate that when calculating vertical vibration frequencies of asymmetry suspension bridge, the influence of side-cable and tower stiffness should not be ignored, and the result of calculated by proposed formulas considering side-cable and tower stiffness is much agreed with that calculated by the finite element method . The error is 3.3%, which meets requirements of accuracy for projects. Therefore, the proposed formulas can be applied to the schematic design and preliminary design of asymmetry suspension bridge.
Key words: bridge engineering     asymmetry suspension bridge     fundamental frequency     Rayleigh's method     tower stiffness    

悬索桥是一种柔性结构，对风和地震等动力荷载非常敏感，悬索桥的自振频率和振型是反映其动力特性的主要参数，它直接影响到结构抗风的稳定性和对地震荷载动力响应，计算悬索桥自振频率和振型是其初步设计中重要一环[1-4]，而对称竖弯基频是计算悬索桥横向屈曲临界风速、驰振临界风速和颤振临界风速的前提，是研究抗风问题的基础.本文对非对称悬索桥的竖向振动基频和非对称结构相关参数之间规律的研究有助于调整结构设计参数.国内外许多学者研究并提出了悬索桥的自由振动频率估算公式，其中李国豪、盛善定等应用Rayleigh法推导了单跨悬索桥各种振型的基频估算公式[3, 4]；肖汝诚采用有限元法和解析法结合的方法同样提出了吊桥的基频近似计算公式[5]；我国《公路桥梁抗风设计规范》(JTG/T D60-01-2004)也给出了单跨简支悬索桥反对称竖向弯曲基频和中跨简支的悬索桥竖向对称弯曲基频估算公式[6]；谢官模考虑了吊杆、索夹等的动能后应用Rayleigh法推导了大跨度悬索桥竖向振动基频的实用近似计算公式[7].以上基于能量法推导的悬索桥基频近似计算公式虽然一定程度上能满足工程精度的要求，但是在推导过程中忽略了主塔对自由振动基频的影响.文献[8]通过有限元软件对虎门大桥、江阴长江大桥、伶仃洋大桥等在不计入和计入边缆和主塔刚度两种情形下的对称竖向弯曲自由振动和扭转振动基频的计算表明，对于对称扭转振动基频计入和不计入边缆和主塔刚度影响计算结果区别不是太大，但是对于竖向弯曲自由振动基频，不计入边缆和主塔刚度影响与计入情况相比，前者计算值普遍大于后者5%~7%，对于研究学者来说这一误差比较客观.为了提高精度，文献[9-13]提出了计入中塔刚度影响的3塔或多塔悬索桥的各种振型的基频估算公式.

上述许多自由振动基频近似计算公式都是基于传统的双塔或多塔的悬索桥，但是实际情况中受工程环境的限制，尤其是在山区出现了非对称悬索桥，很少有文献研究非对称悬索桥，更少有文献研究其基频的定量计算公式.虽然有限元法得到了广泛的应用，对此类桥梁来说，建模过程依然繁琐，不利于技术人员快速判断桥梁结构的振动特性.为此，本文以非对称悬索桥的对称竖弯基频为研究对象，应用能量法，选取合理的振型函数，推导了在计入和不计入边缆和主塔刚度影响两种情况下的非对称悬索桥的对称竖向弯曲自由振动基频近似公式，以供概念设计或校核有限元计算结果.

1 基于Rayleigh法的频率计算方法

根据能量守恒定律，如果忽略阻尼的影响[14]，桥梁体系在振动过程中任何时刻的势能U与动能T之和等于常数C，即对于保守系统，其结构总能量是守恒的，其表达式为

$U+T=\text{C}$    (1)

对于一般振动形式的桥梁，在无阻尼固有振动的情况下，桥梁的任一点、任一瞬间的位移可以表示为

$\text{v}(x,t)=\varphi (x)\sin (\omega t+\theta )$    (2)

其中：φ(x)是假定的能满足桥梁位移边界条件的近似振型函数；ω为与此对应的频率.

根据Rayleigh-Ritz法可得频率ω的近似公式：

${{\omega }^{2}}=\frac{U}{T}=\frac{\int_{0}^{L}{EI(x){{({\phi }''(x))}^{2}}\text{d}x}}{\int_{0}^{L}{m(x){{(\phi (x))}^{2}}\text{d}x}}$    (3)

其中：EI(x)和m(x)分别为弯曲刚度和质量分布值.

为方便下文表述，对下文中的符号作出如下说明：H、Hs为振动引起的主缆水平分力、恒载作用下主缆的水平拉力； Le、ht、θ为主缆的虚拟长度、主塔的高度、边缆与水平方向的夹角；EcAc(EcAc1)、EIv、EtIt为两侧(单侧)主缆的抗弯刚度、加劲梁的抗弯刚度、主塔的平均抗弯刚度；m、mc、mg、mi为主缆和加劲梁单位长度质量、两主缆质量集度之和、顺桥向加劲梁质量集度、第i吊索的质量集度.

1.1 非对称悬索桥基本假定

本文研究是基于悬索桥的挠度理论，为了便于推导非对称悬索桥自由振动时的竖弯基频近似计算公式，基本假定如下：1)不考虑材料的非线性，所使用的材料均满足胡克定律；2)恒载在主缆上沿跨度均匀布置，假定主缆在恒载作用下的线形为抛物线；3)假定吊索沿跨径均匀稠密布置，且在振动时不伸长不倾斜；4)假定桥梁自由振动产生较小幅度的位移，且整个过程结构刚度保持不变；5)假定非对称悬索桥的主索鞍在主塔上不产生滑动等现象.

为了适应山区等特定的工程环境，出现了非对称的悬索桥[15].非对称悬索桥是指非传统的无主塔、主缆不等高支撑和两边跨跨径不等的悬索桥，这些非对称的悬索桥在动力分析方面与传统的悬索桥有较大的差距，本文研究非对称悬索桥竖向自由振动基频是基于主缆不等高支撑的情况.非对称悬索桥两主塔的高差为h、跨中垂度为f、主跨跨径为L时，令矢跨比n=f/L，定义非对称悬索桥结构参数有关的系数m为敏感性参数(m=h/L，为主缆支撑点高差与主跨跨径的比值)，如图 1所示.

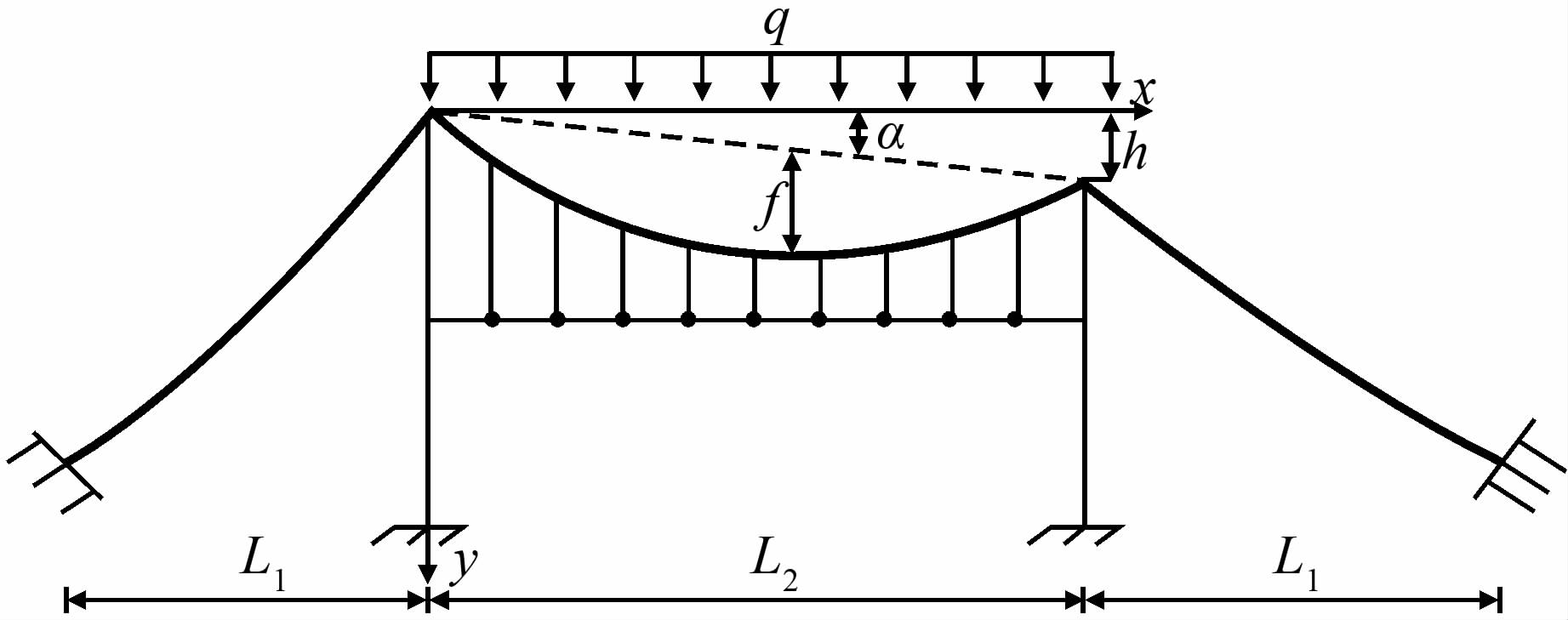
图 1 非对称悬索桥在恒载作用下的示意图 Figure 1 Diagram of dead load of asymmetry suspension bridge
图选项

根据基本假定，主缆线形的函数为

$y=mx+4nx(L-x)/L$    (4)

具有重力刚度的主梁下垂曲线为抛物线，垂直方向的平衡条件为

$-{{H}_{\text{s}}}\frac{{{\text{d}}^{2}}y}{\operatorname{d}{{x}^{2}}}=q$    (5)

将式(5)代入到式(4)，可得恒载作用下水平拉力为

${{H}_{\text{s}}}=q{{L}^{2}}/8f$    (6)
1.2 非对称悬索桥体系势能 1.2.1 主缆势能

由于非对称悬索桥的自由振动是微小的，所以由缆力变化产生的主缆应变能和恒载作用点降低产生的重力势能构成了主缆势能(主缆微元体变形示意图见图 2).

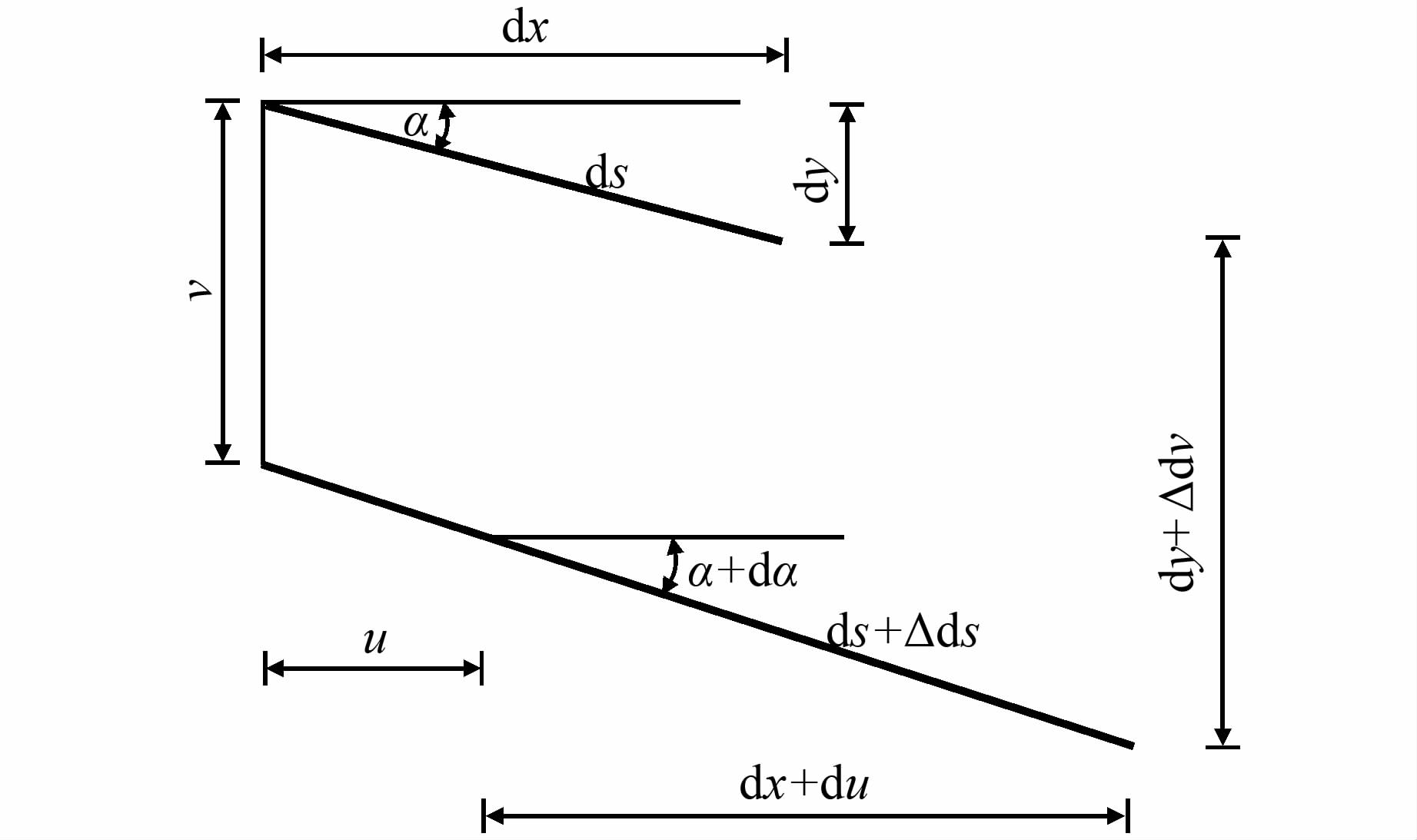
图 2 主缆微元体变形图 Figure 2 Deformation of infinitesimal element of cable
图选项

缆力变化产生的势能为

${{\text{U}}_{\text{ce}}}=\frac{1}{2{{E}_{\text{c}}}}\int{{{\sigma }^{2}}}\text{d}v=\frac{{{H}^{2}}{{L}_{\text{e}}}}{2{{E}_{\text{c}}}{{A}_{\text{c}}}}$    (7)

主缆在作用力下横向变形量为

$\text{d}u=\frac{\text{d}s}{\text{d}x}\Delta \text{d}s+\frac{{{(\Delta \text{d}s)}^{2}}}{2\text{d}x}-\frac{{{(\text{d}u)}^{2}}}{2\text{d}x}-\frac{{{(\text{d}v)}^{2}}}{2\text{d}x}-\frac{\text{d}y}{\text{d}x}\text{d}v$    (8)

忽略高次项(Δds)2和(du)2，得

$\text{d}u=\frac{\text{d}s}{\text{d}x}\Delta \text{d}s-\frac{{{(\text{d}v)}^{2}}}{2\text{d}x}-\frac{\text{d}y}{\text{d}x}\text{d}v$

由cosα=dx/ds得微单元主缆伸长量：

$\Delta \text{d}s=\frac{H\text{d}s/\text{d}x}{{{E}_{\text{c}}}{{A}_{\text{c}}}}\text{d}s=\frac{H}{{{E}_{\text{c}}}{{A}_{\text{c}}}{{\cos }^{2}}\alpha }\text{d}x$

其中，α为主缆线形的倾角.非对称悬索桥主缆的虚拟长度为

$\begin{align} & L{}_{\text{e}}=\int_{0}^{l}{(\frac{\text{d}s}{\text{d}x}}{{)}^{3}}\text{d}x=\int_{0}^{L}{(\frac{1}{\cos \alpha }}{{)}^{3}}\text{d}x= \\ & L(1+8{{n}^{2}}+25.6{{n}^{4}}+1.5{{m}^{2}}+16{{m}^{2}}{{n}^{2}}+0.5{{m}^{4}}) \\ \end{align}$    (9)
$u=\frac{H{{L}_{\text{e}}}}{{{E}_{\text{c}}}{{A}_{\text{c}}}}-\int_{0}^{L}{\frac{\text{d}y}{\text{d}x}\frac{\text{d}v}{\text{d}x}}\text{d}x-\frac{1}{2}\int_{0}^{L}{(\frac{\text{d}v}{\text{d}x}}{{\text{)}}^{2}}\text{d}x$    (10)

忽略高次项，整理得

$u=\frac{H{{L}_{\text{e}}}}{{{E}_{\text{c}}}{{A}_{\text{c}}}}+{y}''\int_{0}^{L}{v}\text{d}x$

由于主缆两端水平位移为0，即

$\frac{H{{L}_{\text{e}}}}{{{E}_{\text{c}}}{{A}_{\text{c}}}}=-{y}''\int_{0}^{L}{v}\text{d}x$    (11)

由式(5)、(7)和(11)得

${{U}_{\text{ce}}}=\frac{{{H}^{2}}{{L}_{\text{e}}}}{2{{E}_{\text{c}}}{{A}_{\text{c}}}}=\frac{Hq}{2{{H}_{\text{s}}}}\int_{0}^{L}{v\text{d}x}$    (12)

不考虑弹性伸长，由恒载作用点降低产生的主缆重力势能为

${{U}_{\text{cg}}}=-\int_{0}^{L}{q}v\text{d}x=-{{H}_{\text{s}}}\int_{0}^{L}{\frac{\text{d}y}{\text{d}x}}\frac{\text{d}v}{\text{d}x}dx=\frac{{{H}_{\text{s}}}}{2}{{\int_{0}^{L}{(\frac{\text{d}v}{\text{d}x})}}^{2}}\text{d}x$    (13)
1.2.2 加劲梁势能

加劲梁的弯曲势能为

${{U}_{\text{s}}}=\frac{1}{2}\int_{0}^{L}{E{{I}_{\text{v}}}}{{(\frac{{{\text{d}}^{2}}v}{\text{d}{{x}^{2}}})}^{2}}\text{d}x$    (14)

因此主缆的势能为

${{U}_{\text{c}}}={{U}_{\text{ce}}}+{{U}_{\text{cg}}}=\frac{Hq}{2{{H}_{\text{s}}}}\int_{0}^{L}{v\text{d}x}+\frac{{{H}_{\text{s}}}}{2}{{\int_{0}^{L}{(\frac{\text{d}v}{\text{d}x})}}^{2}}\text{d}x$    (15)

将式(6)代入式(15)得

${{U}_{\text{c}}}=\frac{2fH}{{{L}^{2}}}\int_{0}^{L}{v\text{d}x}+\frac{{{H}_{\text{s}}}}{2}{{\int_{0}^{L}{(\frac{\text{d}v}{\text{d}x})}}^{2}}\text{d}x$    (16)

体系总势能为

$\begin{align} & U={{U}_{\text{c}}}+{{U}_{\text{s}}}=\frac{4fH}{{{L}^{2}}}\int_{0}^{L}{v\text{d}x}+\frac{{{H}_{\text{s}}}}{2}{{\int_{0}^{L}{(\frac{\text{d}v}{\text{d}x})}}^{2}}\text{d}x+ \\ & \frac{1}{2}\int_{0}^{L}{E{{I}_{\text{v}}}}{{(\frac{{{\text{d}}^{2}}v}{\text{d}{{x}^{2}}})}^{2}}\text{d}x \\ \end{align}$    (17)
1.3 非对称悬索桥体系动能

非对称悬索桥自由振动的动能由主缆的动能、加劲梁的动能和吊杆的动能组成，分别表达如下.

1)主缆的动能：

${{T}_{\text{c}}}=\frac{1}{2}\int\limits_{L}{{{m}_{\text{c}}}}{{(\frac{\partial v}{\partial t})}^{2}}\text{d}x$    (18)

2)加劲梁动能：

${{T}_{\text{g}}}=\frac{1}{2}\int_{L}{{{m}_{\text{g}}}}{{(\frac{\partial v}{\partial t})}^{2}}\text{d}x$    (19)

3)吊索的动能：

${{T}_{\text{h}}}=\sum\limits_{i=1}^{n}{\frac{1}{2}}{{m}_{i}}{{(\frac{\partial {{v}_{i}}}{\partial t})}^{2}}=\frac{{{\omega }^{2}}}{2}\sum\limits_{i=1}^{n}{{{m}_{i}}}{{v}_{i}}^{2}\text{d}x$    (20)

所以结构体系总的动能为

$T={{T}_{\text{c}}}+{{T}_{\text{g}}}+{{T}_{\text{h}}}=\frac{1}{2}\int_{0}^{L}{({{m}_{\text{c}}}+{{m}_{\text{g}}})}{{(\frac{\partial v}{\partial t})}^{2}}\text{dx}+\frac{{{\omega }^{2}}}{2}\sum\limits_{i=1}^{n}{{{m}_{i}}}{{v}_{i}}^{2}\text{d}x$    (21)
2 不计边缆和主塔刚度影响的一阶正对称竖弯基频计算公式

对于一阶正对称竖弯自由振动，其振型如图 3所示.

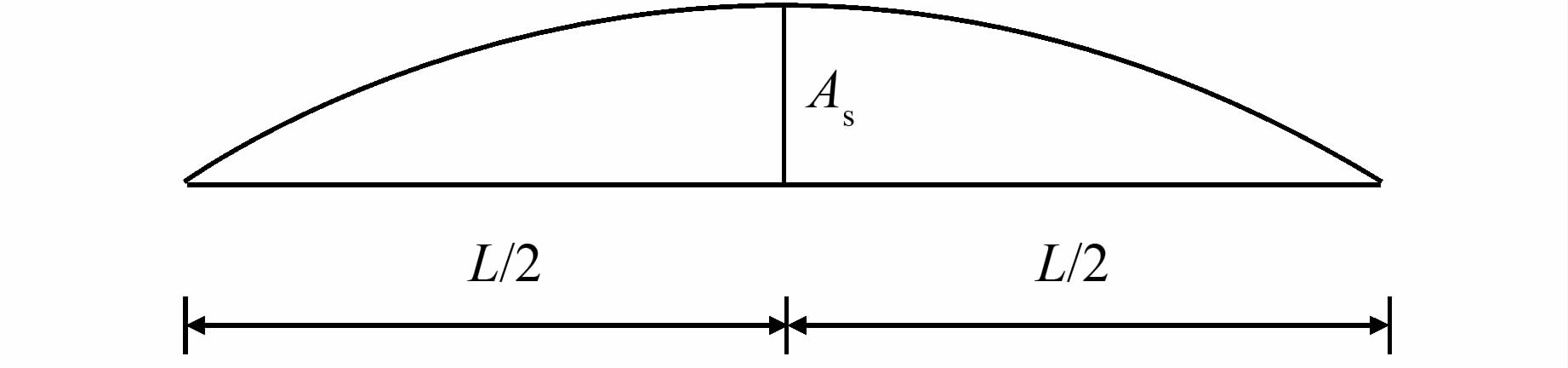
图 3 一阶正对称竖弯振型 Figure 3 Mode shape of 1st symmetric vertical vibration
图选项

假设其满足边界条件的振型函数为

$v={{A}_{\text{s}}}({{x}^{2}}-\frac{{{L}^{2}}}{4})\sin (\omega t+\varphi )x\in (0,L)$    (22)
${{T}_{\max }}={{A}_{\text{s}}}^{2}\left[ \frac{{{L}^{5}}}{60}{{\omega }^{2}}({{m}_{\text{c}}}+{{m}_{\text{g}}})+\frac{{{\omega }^{2}}}{2}{{\sum\limits_{i=1}^{n}{{{m}_{i}}{{v}_{i}}}}^{2}} \right]$    (23)

当sin(ωt+φ)=1时

$\begin{align} & {{U}_{\max }}={{A}_{\text{s}}}^{2}\left( 2E{{I}_{\text{v}}}L+\frac{{{H}_{\text{s}}}{{L}^{3}}}{6}+ \right. \\ & \left. \frac{8{{E}_{\text{c}}}{{A}_{\text{c}}}{{f}^{2}}L}{9\left( 1+8{{n}^{2}}+25.6{{n}^{4}}+1.5{{m}^{2}}+16{{m}^{2}}{{n}^{2}}+0.5{{m}^{4}} \right)} \right) \\ \end{align}$    (24)

将式(23)、(24)代入式(3)可得

$\begin{align} & {{\omega }^{2}}=\left( 2E{{I}_{\text{v}}}L+\frac{{{H}_{\text{s}}}{{L}^{3}}}{6}+ \right. \\ & \frac{8{{E}_{\text{c}}}{{A}_{\text{c}}}{{f}^{2}}L}{9(1+8{{n}^{2}}+25.6{{n}^{4}}+1.5{{m}^{2}}+16{{m}^{2}}{{n}^{2}}+0.5{{m}^{4}})}/ \\ & \left( \frac{{{L}^{5}}}{60}({{m}_{\text{c}}}+{{m}_{\text{g}}})+\frac{1}{2}\sum\limits_{i=1}^{n}{{{m}_{i}}v_{i}^{2}} \right) \\ \end{align}$    (25)
$\begin{align} & {{f}_{1}}=\frac{1}{2\pi }\left[ \left( 2E{{I}_{\text{v}}}L+\frac{{{H}_{\text{s}}}{{L}^{3}}}{6}+ \right. \right. \\ & \left. \frac{8{{E}_{\text{c}}}{{A}_{\text{c}}}{{f}^{2}}L}{9(1+8{{n}^{2}}+25.6{{n}^{4}}+1.5{{m}^{2}}+16{{m}^{2}}{{n}^{2}}+0.5{{m}^{4}})}/ \right) \\ & {{\left. \frac{{{L}^{5}}}{60}({{m}_{\text{c}}}+{{m}_{\text{g}}})+\frac{1}{2}\sum\limits_{i=1}^{n}{{{m}_{i}}v_{i}^{2}} \right]}^{\frac{1}{2}}} \\ \end{align}$    (26)

令mc+mg=q/g=m，将式(9)代入式(26)可得

${{f}_{1}}=\frac{1}{2\text{ }\!\!\pi\!\!\text{ }}\sqrt{\frac{2E{{I}_{\text{v}}}L+\frac{{{H}_{\text{s}}}{{L}^{3}}}{6}+\frac{8{{E}_{\text{c}}}{{A}_{\text{c}}}{{n}^{2}}{{L}^{4}}}{9{{L}_{\text{e}}}}}{\frac{\overline{m}{{L}^{5}}}{60}+\frac{1}{2}{{\sum\limits_{i=1}^{n}{{{m}_{i}}{{v}_{i}}}}^{2}}}}$    (27)

由量级分析可知，为了方便计算，式(27)分子前两项比最后一项小1~2个数量级，近似计算时可忽略不计，分母中吊杆质量远远小于主缆和加劲梁的质量，可忽略吊杆的动能，故式(27)可简化为

${{f}_{1}}=1.16n\sqrt{\frac{E{}_{\text{c}}{{A}_{\text{c}}}}{\overline{m}{{L}_{\text{e}}}L}}$

对于非对称悬索桥两侧主缆虚拟长度可近似为

$L{}_{\text{e}}\approx 2L(1+8{{n}^{2}}+1.5{{m}^{2}})$

一般情况下矢跨比n=0.1，则

${{f}_{1}}=\frac{0.116}{\sqrt{1.08+1.5{{m}^{2}}}L}\sqrt{\frac{E{}_{\text{c}}{{A}_{\text{c1}}}}{\overline{m}}}$    (28)

与《公路桥梁抗风设计规范》[6]中的估算公式${{f}_{\text{b}}}=\frac{0.1}{L}\sqrt{\frac{E{}_{\text{c}}{{A}_{\text{c1}}}}{\overline{m}}}$相比，令$\eta =\frac{1.16}{\sqrt{1.08+1.5{{m}^{2}}}}$，则${{f}_{\text{1}}}=\eta {{f}_{\text{b}}}$.

所以η可以定义为非对称结构参数的影响因子，随着m的增大，η逐渐减小.

3 考虑边缆和主塔刚度影响的一阶正对称竖弯基频计算公式

鞠小华[8]在研究悬索桥边缆和主塔刚度对对称竖向自由振动基频的影响时，分别对比分析了不计入和计入边缆和主塔刚度对自由振动基频的影响下误差的大小，研究结果表明后者误差比前者减小10%左右，所以在计算悬索桥竖向自由振动基频时应该不能忽略边缆和主塔刚度对对称竖向自由振动基频的影响.

当计入边缆和主塔刚度的影响时，要考虑非对称悬索桥自由振动时由于边跨方向和中跨方向主缆拉力差产生的塔顶偏位(如图 4所示)，假设主塔向跨中方向弯曲，塔的偏位为ut(假定两塔的偏位相同)，考虑水平方向平衡，中跨主缆拉力增量H2等于边跨主缆拉力增量H1或H3和塔顶弹性反力之和，塔顶的弹性反力是主塔塔顶弹性位移ut和主塔弹性抗力st的乘积，其中st=3EtIt/ht3，水平方向建立变形协调平衡方程为

${{H}_{2}}={{H}_{1}}+{{s}_{\text{t}}}{{u}_{\text{t}}}={{H}_{1}}+3{{E}_{\text{t}}}{{I}_{\text{t}}}{{u}_{\text{t}}}/{{h}_{\text{t}}}^{3}$    (29)
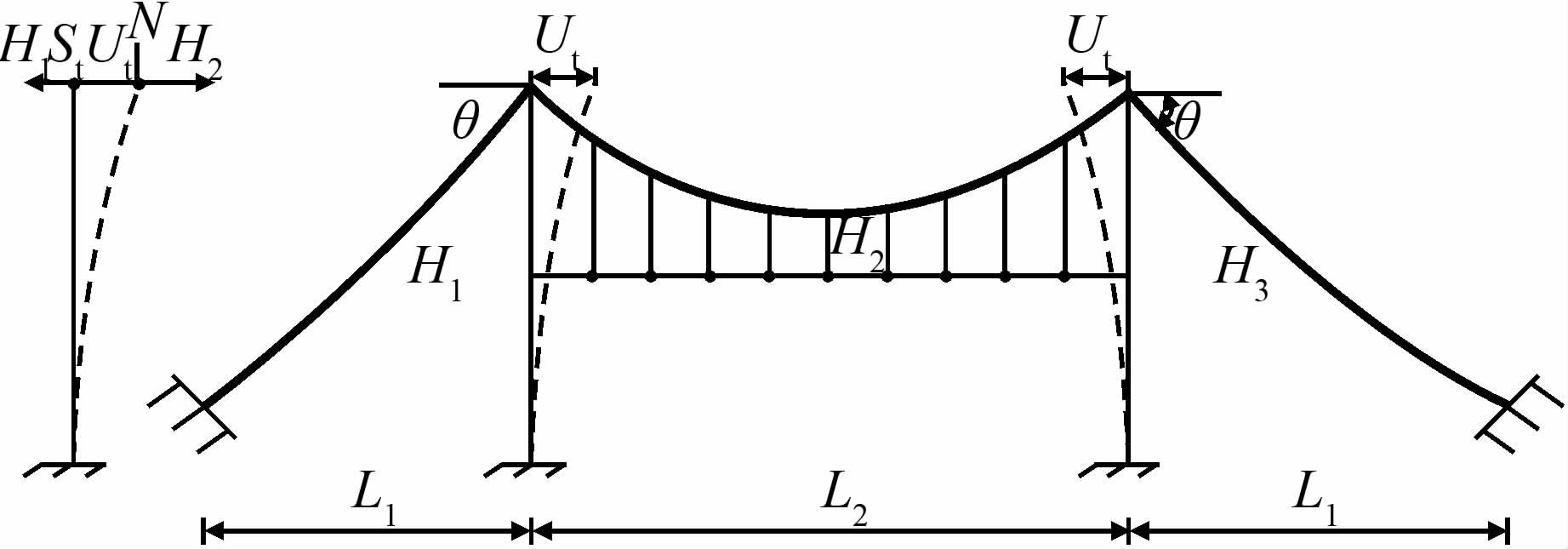
图 4 主塔的变形协调平衡图 Figure 4 Deformation coordination equilibrium diagram of main tower
图选项

主缆因缆力变化引起的势能为

$\overline{{{U}_{\text{ce}}}}=\frac{{{H}_{2}}q}{2{{H}_{\text{s}}}}\int_{0}^{L}{v\text{d}x}$    (30)

恒载作用下主缆降低产生的重力势能为

$\overline{{{U}_{\text{cg}}}}=\frac{{{H}_{\text{s}}}}{2}{{\int_{0}^{L}{(\frac{\text{d}v}{\text{d}x})}}^{2}}\text{d}x$    (31)

主缆的势能为

$\overline{{{U}_{\text{c}}}}=\overline{{{U}_{\text{ce}}}}+\overline{{{U}_{\text{cg}}}}=\frac{Hq}{2{{H}_{\text{s}}}}\int_{0}^{L}{v\text{d}x}+\frac{{{H}_{\text{s}}}}{2}{{\int_{0}^{L}{(\frac{\text{d}v}{\text{d}x})}}^{2}}\text{d}x$    (32)

由于塔顶有水平位移，非对称的悬索桥相容方程可表示为

$-2{{u}_{\text{t}}}=\frac{{{H}_{2}}{{L}_{\text{e}}}}{{{E}_{\text{c}}}{{A}_{\text{c}}}}-\frac{q}{{{H}_{\text{s}}}}\int_{0}^{L}{v\text{d}x}$    (33)

由于边缆的自重相对而言比较小，边跨方向的主缆线形近似可以看作直线，其变形相容方程可以表示为

$\frac{{{H}_{1}}{{L}_{\text{e}}}}{{{E}_{\text{c}}}{{A}_{\text{c}}}}\frac{1}{\cos \theta }={{u}_{\text{t}}}$    (34)

由以上几式可得

${{\text{H}}_{2}}=\frac{{{E}_{\text{c}}}{{A}_{\text{c}}}({{s}_{\text{t}}}{{L}_{1}}+{{E}_{\text{c}}}{{A}_{\text{c}}}\cos \theta )}{2{{E}_{\text{c}}}{{A}_{\text{c}}}{{L}_{1}}+{{L}_{\text{e}}}{{L}_{1}}{{s}_{\text{t}}}+{{E}_{\text{c}}}{{A}_{\text{c}}}\cos \theta }\frac{q}{{{H}_{\text{s}}}}\int_{0}^{L}{v\text{d}x}$    (35)
${{H}_{1}}=\frac{{{E}_{\text{c}}}^{2}{{A}_{\text{c}}}^{2}\cos \theta }{2{{E}_{\text{c}}}{{A}_{\text{c}}}{{L}_{1}}+{{L}_{\text{e}}}{{L}_{1}}{{s}_{\text{t}}}+{{E}_{\text{c}}}{{A}_{\text{c}}}\cos \theta }\frac{q}{{{H}_{\text{s}}}}\int_{0}^{L}{v\text{d}x}$    (36)
${{u}_{\text{t}}}=\frac{{{E}_{\text{c}}}{{A}_{\text{c}}}{{L}_{1}}}{2{{E}_{\text{c}}}{{A}_{\text{c}}}{{L}_{1}}+{{L}_{\text{e}}}{{L}_{1}}{{S}_{1}}+{{E}_{\text{c}}}{{A}_{\text{c}}}L{}_{\text{e}}\cos \theta }\frac{q}{{{H}_{\text{s}}}}\int_{0}^{L}{v}\text{d}x$    (37)

设$\overline{L}=\frac{2{{E}_{\text{c}}}{{A}_{\text{c}}}{{L}_{1}}+{{L}_{\text{e}}}{{L}_{1}}{{s}_{\text{t}}}+{{L}_{\text{e}}}{{E}_{\text{c}}}{{A}_{\text{c}}}\cos \theta }{{{s}_{\text{t}}}{{L}_{1}}+{{E}_{\text{c}}}{{A}_{\text{c}}}\cos \theta }$

$\begin{align} & {{H}_{2}}=\frac{{{E}_{\text{c}}}{{A}_{\text{c}}}}{{\bar{L}}}\frac{q}{{{H}_{\text{s}}}}\int_{0}^{L}{v\text{d}x} \\ & \overline{{{T}_{\max }}}={{A}_{\text{s}}}^{2}\left[ \frac{{{L}^{5}}}{60}{{\overline{\omega }}^{2}}({{m}_{\text{c}}}+{{m}_{\text{g}}})+\frac{{{\overline{\omega }}^{2}}}{2}\sum\limits_{i=1}^{n}{{{m}_{i}}v_{i}^{2}} \right] \\ \end{align}$    (38)
$\overline{{{U}_{\max }}}={{A}_{\text{s}}}^{2}(2E{{I}_{\text{v}}}L+\frac{{{H}_{\text{s}}}{{L}^{3}}}{6}+\frac{8{{E}_{\text{c}}}{{A}_{\text{c}}}{{f}^{2}}{{L}^{2}}}{9\overline{L}})$    (39)

将式(38)、(39)代入式(3)可得

$\overline{{{f}_{1}}}=\frac{1}{2\text{ }\!\!\pi\!\!\text{ }}\sqrt{\frac{2E{{I}_{\text{v}}}L+\frac{{{H}_{\text{s}}}{{L}^{3}}}{6}+\frac{8{{E}_{\text{c}}}{{A}_{\text{c}}}{{n}^{2}}{{L}^{4}}}{9\overline{L}}}{\frac{q{{L}^{5}}}{60g}+\frac{1}{2}{{\sum\limits_{i=1}^{n}{{{m}_{i}}{{v}_{i}}}}^{2}}}}$    (40)

同理公式简化

${{\overline{f}}_{1}}=1.16n\sqrt{\frac{E{}_{\text{c}}{{A}_{\text{c1}}}}{\overline{m}\overline{L}L}}$    (41)

令

$\beta =\frac{\overline{L}}{{{L}_{\text{e}}}}=1-\frac{1}{1+\frac{L\cos \theta }{{{L}_{1}}}+\frac{3{{E}_{\text{t}}}{{I}_{\text{t}}}L}{{{E}_{\text{c}}}{{A}_{\text{c}}}{{h}_{\text{t}}}^{3}}}$    (42)

式中，β定义为边缆和主塔刚度对对称竖向弯曲振动频率的影响系数，则

${{\overline{f}}_{1}}=\sqrt{\beta }\frac{1.16n}{\sqrt{1+8{{n}^{2}}+1.5{{m}^{2}}}L}\sqrt{\frac{E{}_{\text{c}}{{A}_{\text{c1}}}}{\overline{m}}}$    (43)

若矢跨比n=0.1，则

${{\overline{f}}_{1}}=\sqrt{\beta }\frac{0.116}{\sqrt{1.08+1.5{{m}^{2}}}L}\sqrt{\frac{E{}_{\text{c}}{{A}_{\text{c1}}}}{\overline{m}}}$    (44)

与《公路桥梁抗风设计规范》[6]中的估算公式${{f}_{\text{b}}}=\frac{0.1}{L}\sqrt{\frac{E{}_{\text{c}}{{A}_{\text{c1}}}}{\overline{m}}}$相比，令

$\begin{align} & \gamma =\sqrt{\beta }\frac{1.16}{\sqrt{1.08+{{m}^{2}}}}= \\ & \sqrt{1-\frac{1}{1+\frac{L\cos \theta }{{{L}_{1}}}+\frac{3{{E}_{\text{t}}}{{I}_{\text{t}}}L}{{{E}_{\text{c}}}{{A}_{\text{c}}}{{h}_{\text{t}}}^{3}}}}\frac{1.16}{\sqrt{1.08+{{m}^{2}}}} \\ \end{align}$

则$\overline{{{f}_{1}}}=\gamma {{f}_{\text{b}}}$.所以γ可以定义为计入边缆和主塔刚度的非对称参数的影响因子.

4 算例验证

某特大桥为主跨628m的单跨主缆不等高支撑的非对称悬索桥，跨径分布为166 m+628 m+166 m，上部结构采用抗风性能较好的扁平流线型钢箱梁.设计主缆矢跨比为1/10，主缆横桥向中心间距为26 m，吊索顺向标准间距为12 m.索塔采用钢筋混凝土塔柱结构，外形为门式框架.塔体包括塔顶、上塔柱、中塔柱和下塔柱，塔柱之间设3道横梁.塔柱采用矩形空心薄壁截面.由于受地形的限制，两主塔是非对称布置的，索塔高差为10.362 m，且索塔左右塔柱采用不等高的形式，高塔肢高153.5 m，矮塔肢高138.5 m.

1) 方法1：有限元法求解

建立有限元模型，计算得到非对称悬索桥的一阶对称竖弯自振基频f1=0.301Hz，振型如图 5所示.

图 5 数值模型的模态分析结果 Figure 5 Modal analysis result of numerical model
图选项

2) 方法2：文中简化公式求解

实用计算公式中的计算所需参数如表 1所示.

表 1 计算参数一览表 Table 1 Calculation parameters list
主跨跨径
L/m		矢跨比
n		敏感性参数
m		主缆弹模
Ec/(N·m-2)		主缆面积
Ac/m2		主缆和桥面系单位长度
质量m/(kg·m-1)
6280.10.0171.98×10110.33819 490
边跨跨径
L1/m		边缆与水平方向夹角
θ/°		主塔平均高度
ht/m		主塔弹模
Et/(N·m-2)		主塔截面惯性矩
It/m4
166251463.45×1010324
表选项

将表 1参数代入式(28)、(42)和(44)可得f1=0.33 Hz，β=0.779，$\overline{{{f}_{1}}}=\sqrt{\beta }{{f}_{1}}=0.291$=0.291 Hz.

3) 计算结果比较

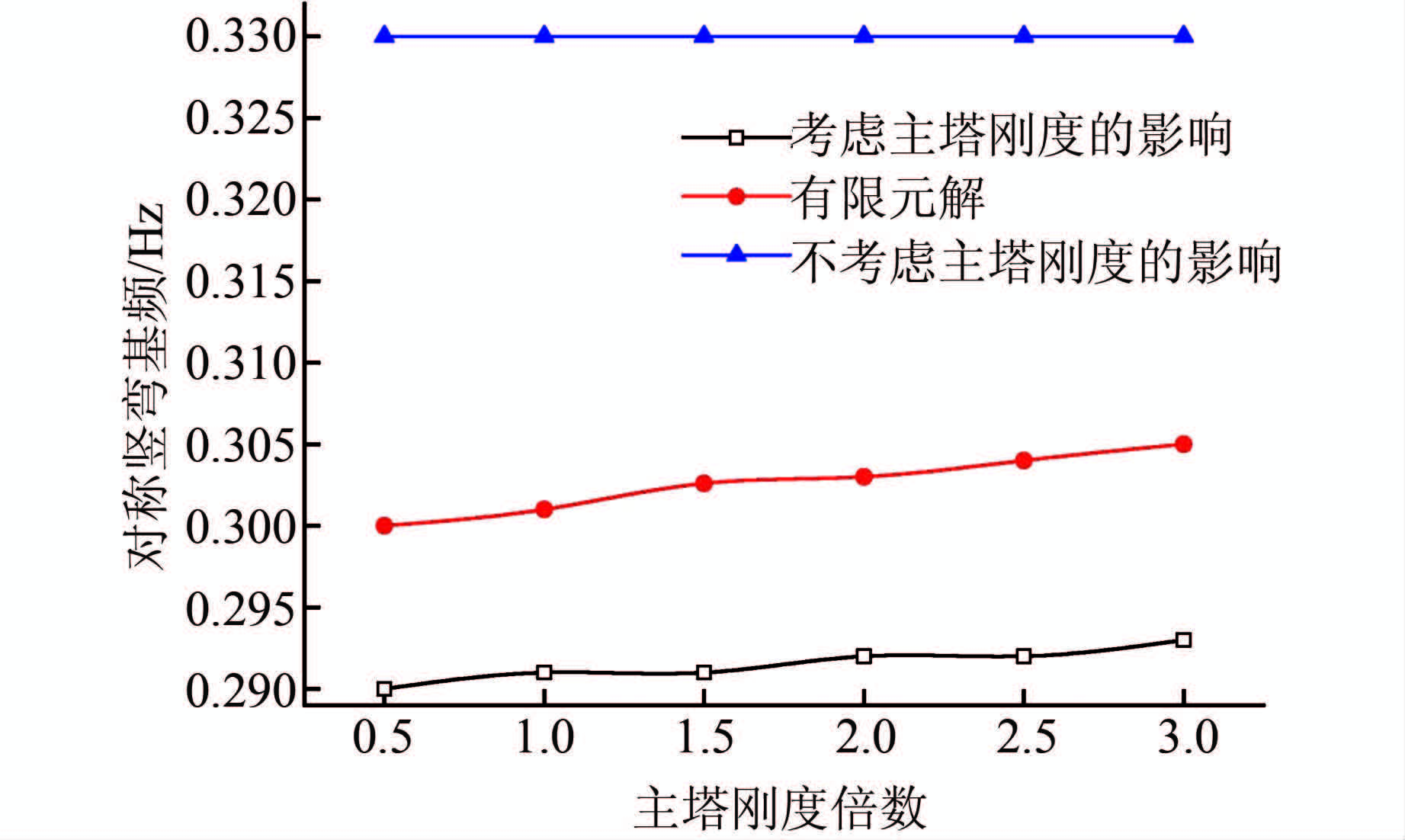
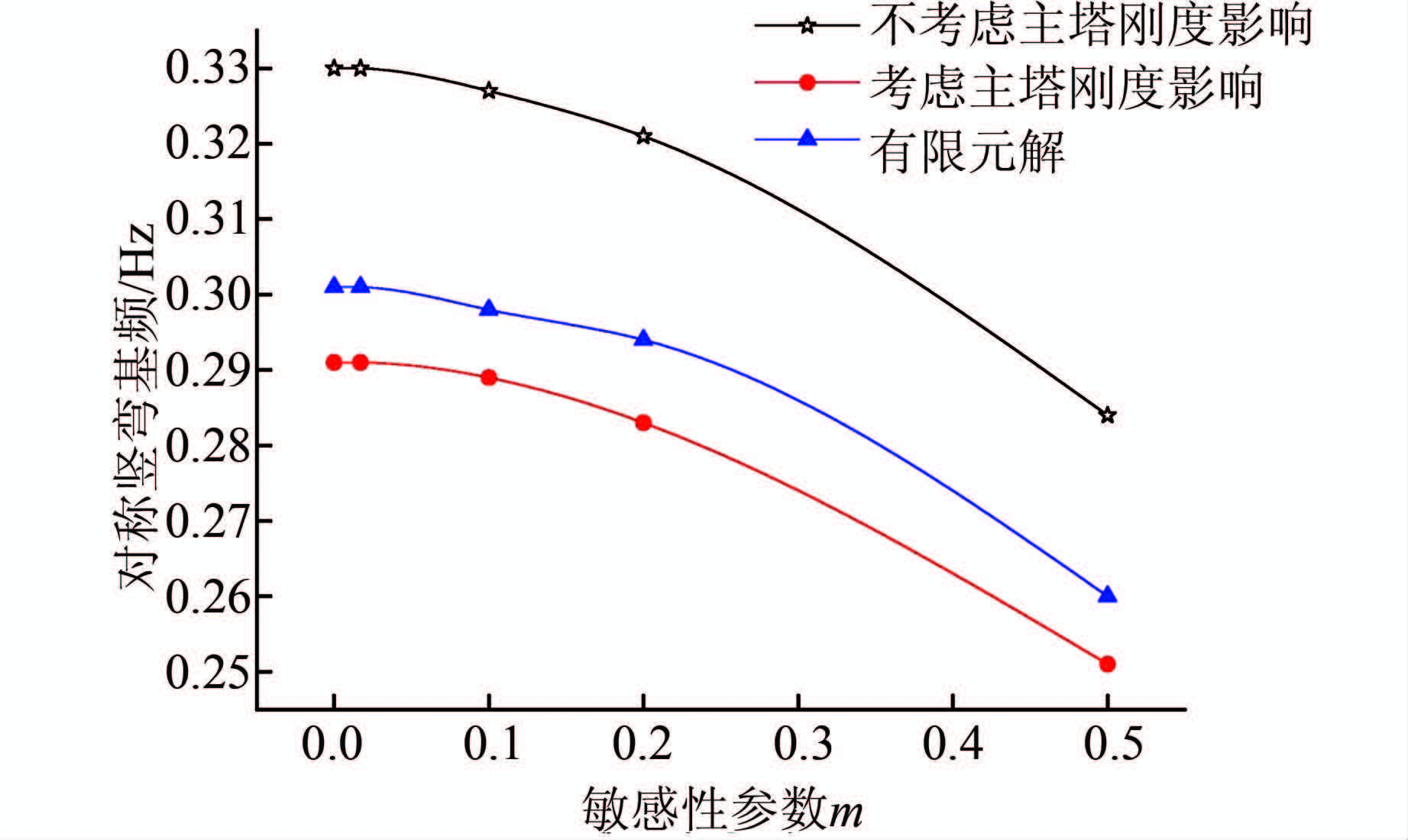
由表 2可以得出，计入边缆和主塔刚度的影响时可以减小误差，近似公式计算结果与有限元误差可以从9.6%降到3.3%.由图 6分析可知，不计入主塔刚度影响时的基频在主塔刚度发生变化时保持不变，考虑主塔刚度影响时的解析解和有限元解随着主塔刚度倍数的增大，一阶正对称竖向自振基频逐渐增大，但是变化幅度不是很大，相当于主塔刚度增加一倍时，基频只增加0.67%.由图 7分析可知，考虑和不考虑主塔刚度的解析解和有限元解都受非对称悬索桥结构敏感性参数m的影响，当m较小时，对称竖弯基频变化不大，但当m＞0.1时，基频减小的幅度逐渐增大，说明结构整体刚度减小的幅度显著增大，这个规律可以指导非对称悬索桥的初步设计.由图 6和图 7分析可知，计入主塔刚度影响的结果更接近有限元解，所以为了提高精度不能忽略边缆和主塔刚度的影响.

表 2 一阶对称竖弯基频对比 Table 2 Comparison of 1st symmetric fundamental frequencies of vertical vibration
工况基频/Hz 频率差/Hz误差/%
有限元文中方法
不考虑边缆和
主塔刚度		0.3010.3300.0299.6
考虑边缆和
主塔刚度		0.3010.291-0.0133.3
表选项
图 6 主塔刚度对对称竖向振动基频的影响 Figure 6 Influence of tower stiffness on fundamental frequencies of vertical vibration
图选项
图 7 敏感性参数对对称竖弯基频的影响 Figure 7 Influence of sensitivity parameter on fundamental frequencies of vertical vibration
图选项
5 结论

1) 推导了非对称悬索桥在不计入和计入边缆和主塔刚度两种情况下的竖向对称自振基频的近似计算公式，提出了非对称悬索桥结构敏感参数m对一阶竖向对称自振基频的影响因子η，以及推导了边缆和主塔刚度对竖向对称弯曲振动频率的影响系数β的表达式，给出了计入边缆和主塔刚度的非对称结构参数的影响因子γ.

2) 分别计算了不计入和计入边缆和主塔刚度两种情况下的非对称悬索桥的竖向弯曲自振基频，结果表明不计入边缆和主塔刚度影响时有限元解和计算值误差为9.6%，而计入情况下的误差仅为3.3%，所以在计算非对称悬索桥基频不能忽略边缆和主塔刚度的影响.

3) 本文推导的对称竖弯频率实用计算公式适用于主缆不等高支撑的双塔悬索桥，3塔或多塔体系及其他体系应做专门研究.

参考文献
[1] Ren W X, Blandford G E, Harik I E. Finite-element model and free vibration response[J]. Journal of Bridge Engineering, 2004, 9(2): 110–118. DOI:10.1061/(ASCE)1084-0702(2004)9:2(110)
[2] 刘春华, 秦权. 桥梁结构固有频率的统计特征[J]. 中国公路学报, 1997, 10(4): 49–54.
Liu Chunhuan, Qin Quan. Statistics of natural frequencies for bridge structures[J]. China Journal of Highway and Transport, 1997, 10(4): 49–54.
[3] 李国豪. 桥梁结构稳定与振动[M]. 北京: 中国铁道出版社, 2002.
Li Guohao. Stability and Vibration of Bridge Structures[M]. Beijing: China Railway Publishing House, 2002.
[4] 盛善定, 袁万城, 范立础. 悬索桥振动基频的实用估算公式[J]. 东北公路, 1996(1): 71–76.
Sheng Shanding, Yuan Wancheng, Fan Lichu. Practical estimation formula of vibration basic frequency of suspension bridge[J]. Northeast Highways, 1996(1): 71–76.
[5] 肖汝诚. 吊桥结构自振频率的计算方法[J]. 华东公路, 1991, 2(1): 54–58.
Xiao Rucheng. Method calculate natural vibration frequency of suspension bridge[J]. East Road, 1991, 2(1): 54–58.
[6] 中华人民共和国交通部. JTG/T D60-01-2004 公路桥梁抗风设计规范[S]. 北京: 人民交通出版社, 2004.
Ministry of Transportation of the People’s Republic of China.JTG/T D60-01-2004 Wind-resistant Design Specification for Highway Bridges[S].Beijing: China Communications Press,2004.
[7] 谢官模, 王超. 大跨度悬索桥竖向振动基频的实用近似计算公式[J]. 固体力学学报, 2008, 29(12): 200–203.
Xie Guanmo, Wang Chao. Approximate formula of fundamental vertical frequencies of large-span suspension bridge[J]. Chinese Journal of Solid Mechanics, 2008, 29(12): 200–203.
[8] 鞠小华, 廖海黎, 沈锐利. 对悬索桥对称竖弯基频近似公式的修正[J]. 土木工程学报, 2002, 35(1): 44–49.
Ju Xiaohua, Liao Haili, Shen Ruili. Modification on simplified formula of symmetric-vertical natural frequencies for suspension bridges[J]. China Civil Engineering Journal, 2002, 35(1): 44–49.
[9] 鞠小华. 三跨连续加劲梁悬索桥基频近似公式[J]. 铁道工程学报, 2003(2): 59–63.
Ju Xiaohua. Approximate formulas of calculating primary frequencies for three-span continuous girder suspension bridge[J]. Journal of Rail Way Engineering Society, 2003(2): 59–63.
[10] 张超, 黄群君, 许莉. 考虑主塔刚度影响的三塔自锚式悬索桥竖弯频率计算公式[J]. 长安大学学报(自然科学版), 2014, 34(6): 100–106.
Zhang Chao, Huang Qunjun, Xu Li. Frequency formulas for vertical vibration of three-tower self-anchored suspension bridge considering tower stiffness influence[J]. Journal of Chang’an University: Natural Science Edition, 2014, 34(6): 100–106.
[11] 张超. 多塔自锚式悬索桥竖弯基频简化计算[J]. 武汉理工大学学报:交通科学与工程版, 2013, 37(4): 753–757.
Zhang Chao. Simplified calculation of primary vertical frequencies for multi-tower self-anchored suspension bridge[J]. Journal of Wuhan University of Technology(Transportation Society &Engineering), 2013, 37(4): 753–757.
[12] 王本劲, 马如进, 陈艾荣. 多塔连跨悬索桥基频估算实用公式[J]. 公路交通科技, 2012, 29(11): 58–62.
Wang Benjin, Ma Rujin, Chen Airong. Practical formula of fundamental frequency estimation for multi-pylon suspension bridge[J]. Journal of Highway and Transportation Research and Development, 2012, 29(11): 58–62.
[13] 王本劲, 马如进, 陈艾荣. 多塔连跨悬索桥基频估算方法[J]. 结构工程师, 2011, 27(6): 54–58.
Wang Benjin, Ma Rujin, Chen Airong. Estimation of fundamental frequency of multi-pylon suspension bridges[J]. Structural Engineers, 2011, 27(6): 54–58.
[14] 周勇军, 张晓栋, 宋一凡, 等. 高墩连续刚构桥纵向振动基频的能量法计算公式[J]. 长安大学学报:自然科学版, 2013, 33(3): 48–54.
Zhou Yongjun, Zhang Xiaodong, Song Yifan, et al. Calculation formula of longitude fundamental vibration frequency for continuous rigid frame bridge with higher pier based on energy method[J]. Journal of Chang’an University: Natural Science Edition,, 2013, 33(3): 48–54.
[15] 李智宇. 非对称悬索桥设计方法研究[D].西安:长安大学, 2006.
Li Zhiyu. Research of design methods for asymmetry suspension bridge[D]. Xi’an: Chang’an University, 2006.