文章信息
- 张红梅, 韩万刚
- ZHANG Hongmei, HAN Wangang
- FIR滤波器时延分析及其在信号融合中的应用
- Time-delay analysis of FIR filter and its application to signal fusion
- 武汉大学学报(工学版), 2016, 49(2): 303-308
- Engineering Journal of Wuhan University, 2016, 49(2): 303-308
- http://dx.doi.org/10.14188/j.1671-8844.2016-02-025
-
文章历史
- 收稿日期: 2015-03-11
数字滤波器因其灵活性大、精度高、可靠性好以及易于大规模集成等优点,在数字通信、图像处理、谱分析、模式识别和自动控制等领域得到了广泛的应用[1-2]。
有限脉冲响应(FIR,Finite Impulse Response)滤波器可以在保证任意幅频特性的同时具有严格的线性相频特性,而且其单位抽样响应为有限长,保证了其具有良好的稳定性[3-4]。然而,在实际应用中,不但要求滤波器具有良好的幅频特性,而且要求滤波处理前和滤波处理后的信号保持时间上的一致性。采用常规的FIR数字滤波器滤波后的信号均会存在一定程度的时延,特别是在数据量比较少的情况下,这一现象将会非常明显,不利于信号后期处理和利用[5-9]。此外,在有些闭环系统中,时延的存在将导致系统不稳定。
针对FIR数字滤波器在实际滤波过程中存在时延的现象,许多学者进行了研究,提出了相应的解决方法,这些方法在具体的应用中取得了较好的效果。文献[10]采用基于波形匹配的方法消除了时延;文献[11]提出了一种基于单零点FIR滤波器系数方法消除接收信号的时延;文献[12]提出一种适用于微纳卫星通信系统的窄带信号数字下变频的M点平均降速算法,通过采用数据移位和减少数据位宽的方法,解决了时延问题。上述研究多从具体应用背景出发,给出了消除时延的具体方法,并取得了较为满意的效果。但当这些方法应用到其他场合时,常常难以取得理想效果。为此,本文首先从FIR滤波器的相位特性出发,从理论上进行推导和分析,给出FIR数字滤波器时延消除模型。为进一步验证所得结论的正确性,将该模型应用到实际信号的滤波处理中,取得了理想的效果。
1 理论分析与模型推导FIR数字滤波器输出y(n)可以表示为
式中:N为滤波器的抽头数(或阶数);x(i)表示第i时刻的输入样本;h(i)为FIR滤波器的第i级抽头系数。
下面就FIR数字滤波器冲激响应h(n)的对称性特点及与之对应的频率特性进行讨论。
FIR滤波器的冲激响应序列只需满足奇对称或偶对称条件,就可以实现严格意义上的线性相位特性。由于当h(n)为奇对称时的滤波器只适合做希尔伯特变换器,微分器和正交网络等特殊滤波器;而只有当h(n)为偶对称时的滤波器才可以做一般意义上的FIR滤波器。因此本文只对h(n)为偶对称时的情况进行分析,即有:
以下分两种情况分别进行讨论:
第一种情况: N为奇数时,其频率响应为
化简得:
式中:$A(\omega )=\sum\limits_{l=0}^{\frac{N-1}{2}}{a(l)\cos l\omega }$,称为幅频函数;$\phi (\omega )=-\frac{N-1}{2}\omega $,称为相位函数,它是频率ω的线性函数。
第二种情况:N为偶数时,其频率响应为
式中:$A(\omega )=\sum\limits_{n=0}^{\frac{N}{2}-1}{2h(n)\cos \omega (\frac{N-1}{2})-n}$,为其幅频函数;$\phi (\omega )=-\frac{N-1}{2}\omega $,为相位函数;φ(ω)也是频率ω的线性函数。
由以上两种情况可知,FIR滤波器的相位特性只取决于h(n)的对称性,而与h(n)的取值无关。
综合以上分析可得出如下结论:FIR数字滤波器具有线性相位的充要条件为单位冲激响应h(n)序列必须满足特定的对称性,其相位延迟应等于h(n)长度的一半,即:
式中:N′表示窗口长度,N=N′-1,N为滤波器阶数,故可得FIR数字滤波器相位延迟是其滤波阶数的一半,即:
相位延迟是FIR数字滤波器产生时延的最根本原因,二者关系为
故FIR数字滤波器的时延与滤波阶数N存在如下关系:
根据以上分析,在进行FIR数字滤波器设计时,为了消除FIR数字滤波器对滤波后信号造成的时延,可以将滤波后的信号在上述确定模型基础上通过平移变换即可。
为进一步验证上述结论,下面将其应用到多波束测深系统中GPS高程信号和Heave信号的有效频段提取及融合中。
2 信号有效频段提取 2.1 应用背景多波束测深系统已经广泛应用于河道/海道测量中,其换能器处瞬时高程精度是影响该系统垂直方向最终成果精度的主要因素之一。在传统的多波束测量系统中,参考点的瞬时高程由潮位、吃水和Heave信号联合提供[13]。由于有效Heave信号周期(小于15 s)、吃水周期(15~60 s)和潮位周期(至少大于15~30 min)的不同,就频段的分布特征而言,这三者联合提供的换能器处的瞬时高程丢失了频段范围在60 s到15 min之间的周期性垂直运动信号,这给多波束在高程上的最终测量结果带来约±10 cm左右的误差。
针对传统多波束测深系统数据处理模式存在的问题,研究利用Heave信号中的短周期信号与GPS高程信号中的中、长周期信号,融合成一个反映船体全频段垂直运动的信号,从而消除传统方法因合成信号频段遗漏所造成的测量误差;同时还可以消除船速突变对测量造成的影响,提高瞬时高程确定精度[14]。
目前,GPS采样频率至少为1Hz,根据数字信号处理理论,GPS高程信号至少可以反映周期大于2 s的船体周期性垂直运动。如前所述,Heave信号的有效周期段小于15 s,因而,参考点处的GPS高程信号和Heave信号具有公共的周期分布段(如图 1),故利用这两个信号融合可产生一个无频段遗漏的信号。

|
| 图 1 Heave信号和GPS高程信号周期分布图 Figure 1 The periodic distribution of Heave and GPS height signal |
为了得到一个既能反映Heave信号高频信息、又能反映GPS中、低频特性的信号,在进行Heave信号和GPS高程信号融合前,需对它们分别进行数字滤波处理,提取出有效频段的信号。为此,需要设置一个合适的截止频率,根据上述两信号的频段分布特征,将截止周期设为10 s(即截止频率fsc为0.1 Hz)。分别提取出Heave信号的高频段部分和GPS高程信号的中低频段部分,然后将二者融合成一个反映船体全频段垂直运动的信号,从而消除传统方法因合成信号频段遗漏所造成的测量误差,提高多波束测量成果的精度。
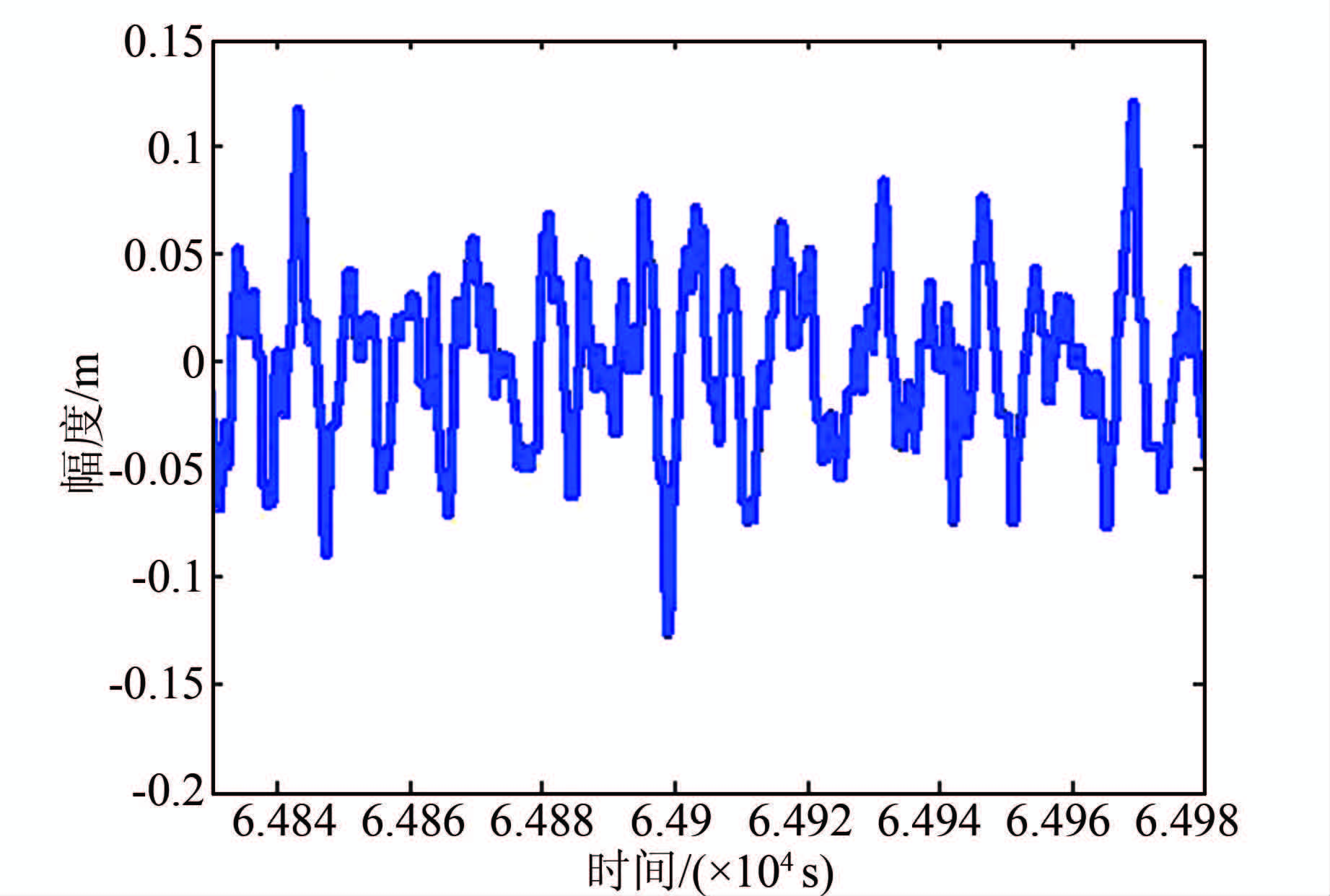
2.2 有效频段Heave信号提取图 2为一段实测的Heave信号时域图,采样频率fs1=4 Hz。根据上述分析和已有研究,Heave信号的高频段有效。因此,需要对其进行高通滤波,提取出有效高频段信号。
|
| 图 2 滤波前Heave信号 Figure 2 Heave signal before being filtered |
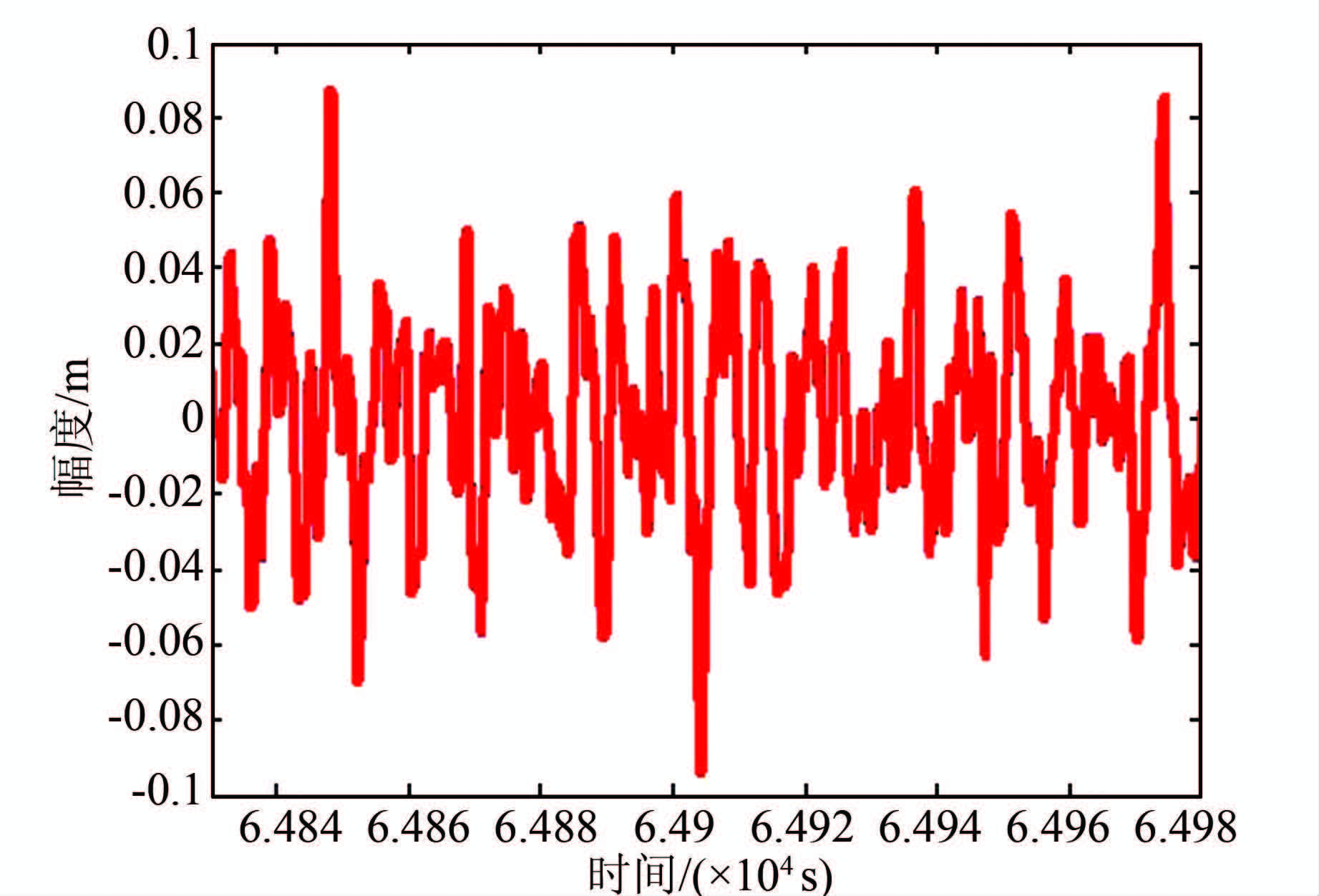
图 3为Heave信号经过阶数为40、截止周期为10 s的传统FIR数字高通滤波器的输出。若将滤波处理前和滤波处理后的Heave信号进行比较(如图 4),不难发现滤波后的信号存在着明显的时延。
|
| 图 3 滤波后Heave信号(N=40) Figure 3 The filtered Heave signal (N=40) |

|
| 图 4 Heave信号滤波前后对比(N=40) Figure 4 The comparison between Heave signal before and after being filtered (N=40) |
为消除时延,直接从信号波形出发,对时延量做更深入的分析。
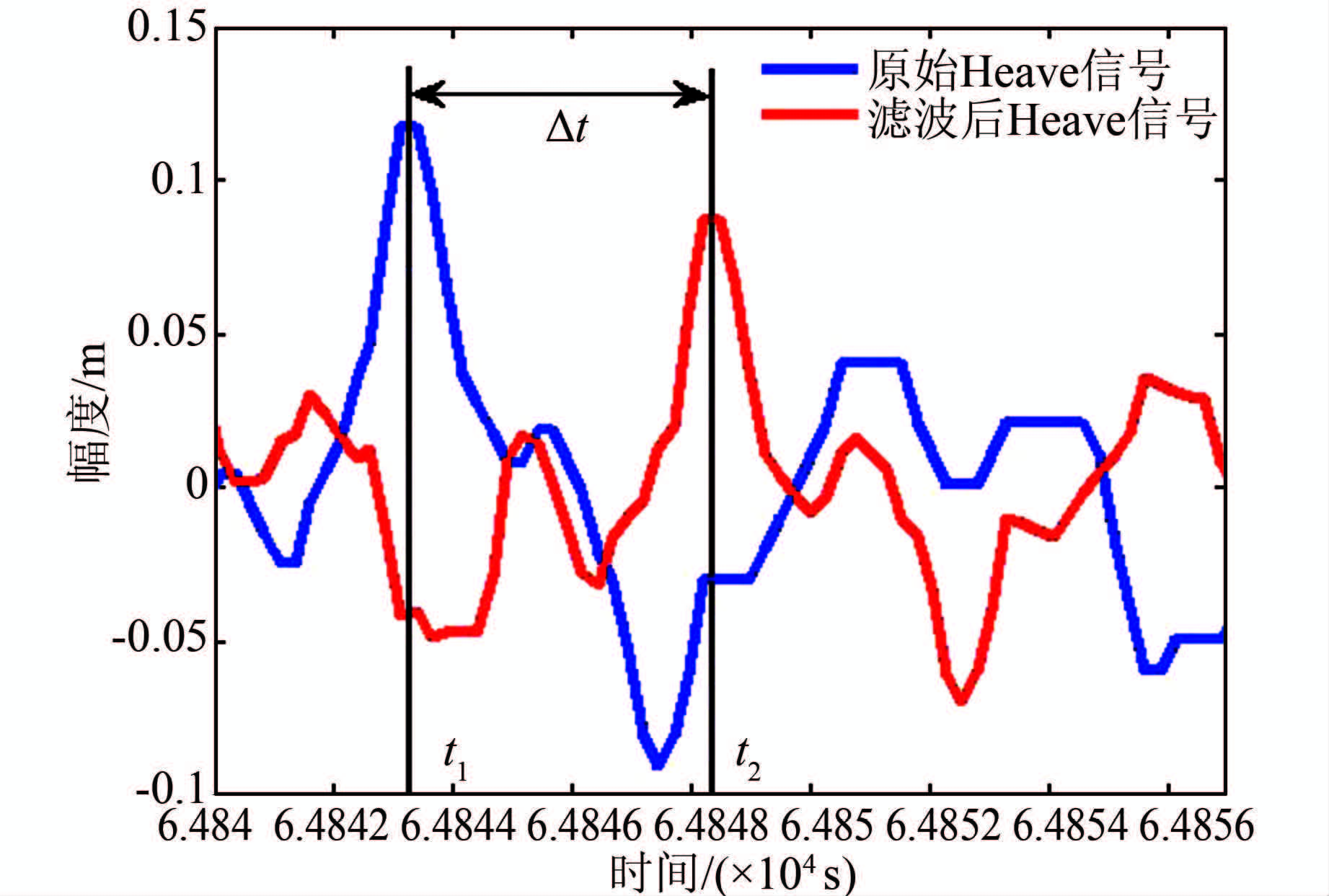
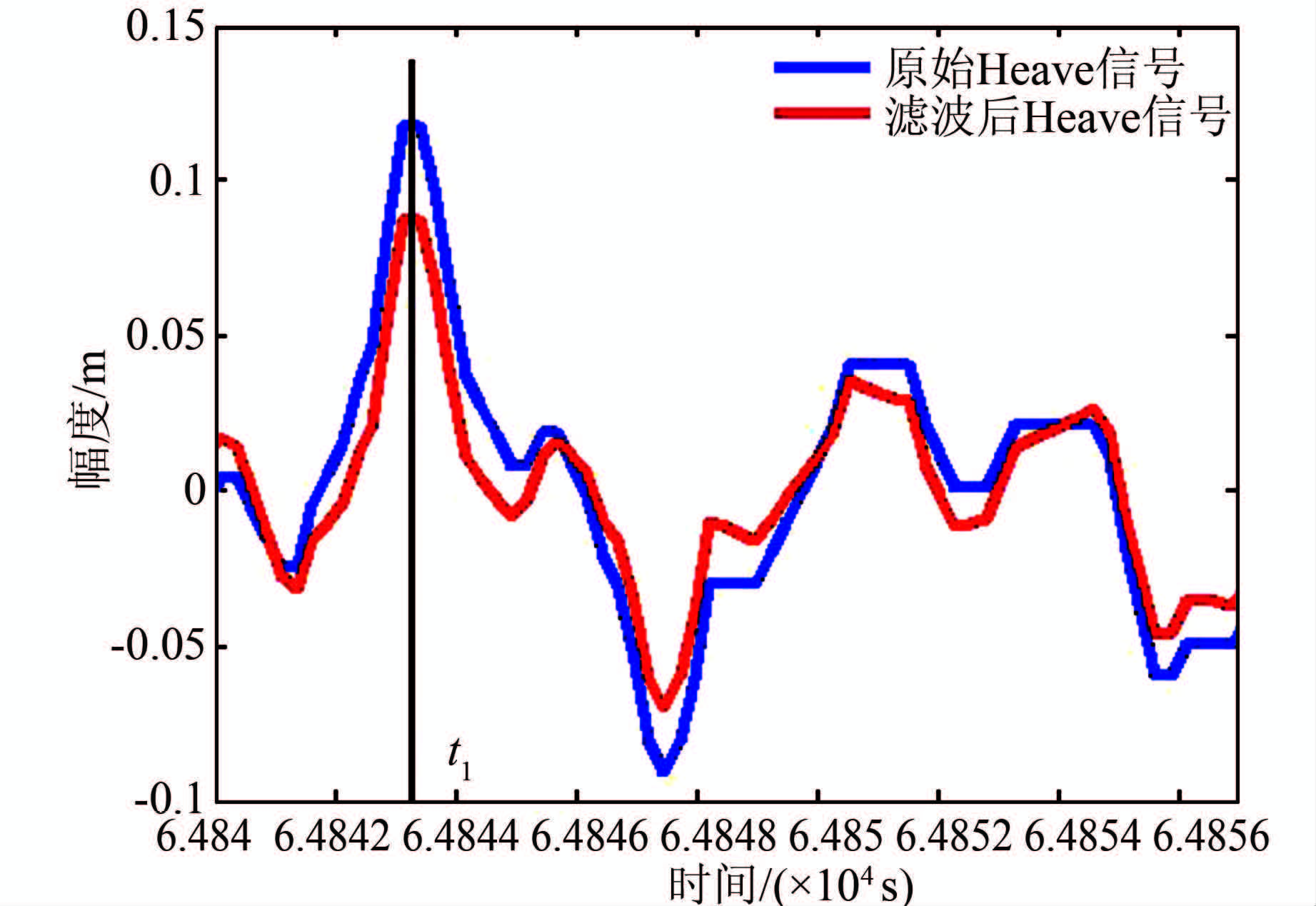
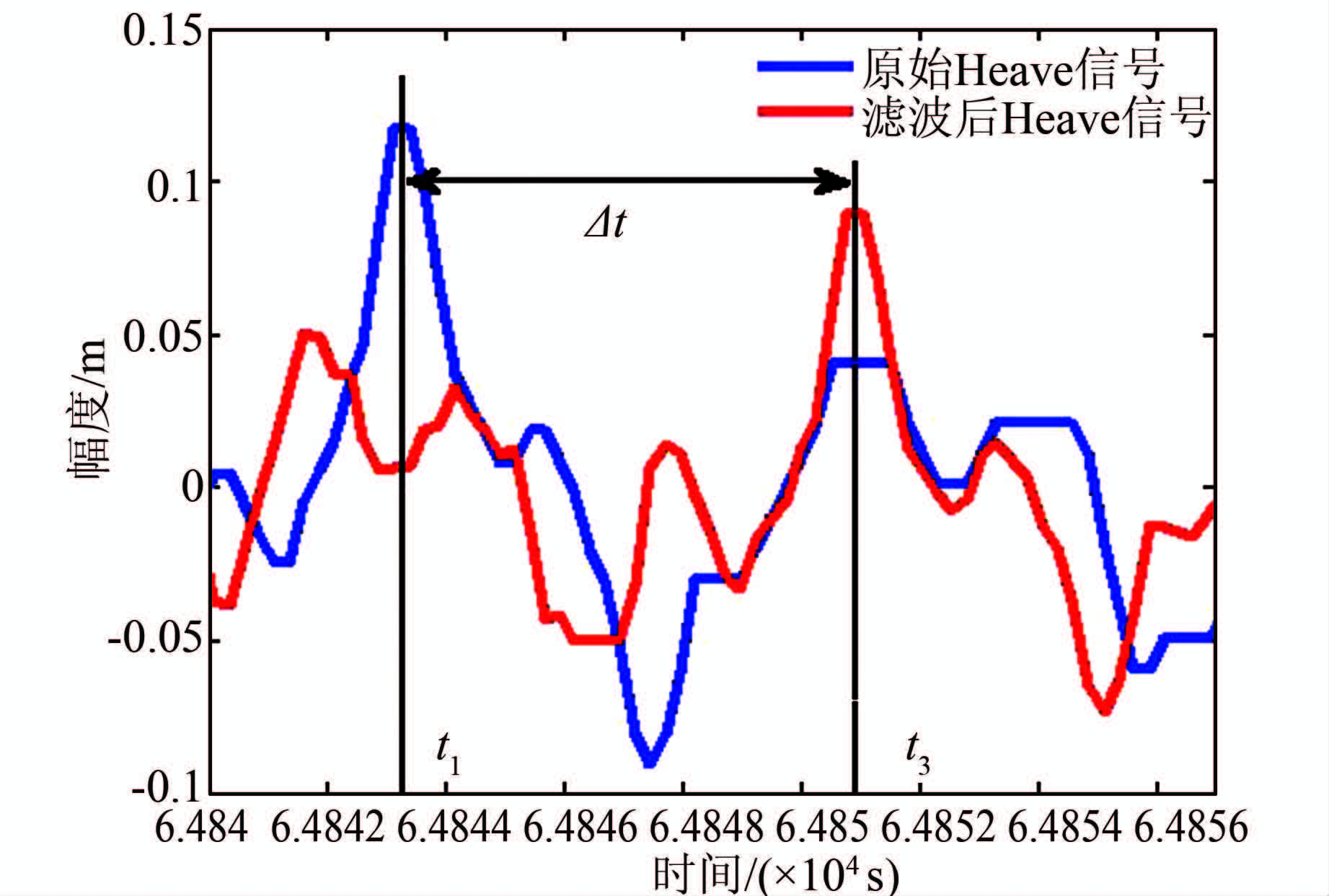
为了确定滤波后信号时延量的大小,截取图 4中区间为[64840,64857]的信号,得图 5所示的Heave信号滤波前、后时域对比图。取原始Heave信号中t1时刻为参考点,则对应的滤波后的Heave信号出现在t2时刻。如果将滤波后的Heave信号向前平移Δt=t2-t1时间,则这两个信号波形一致,且在t1时刻幅值都达到最大值(如图 6)。这表明经过平移以后时延已经被消除;从时间刻度上分析,t1=64 843.5 s,t2=64 848.5 s,此FIR高通数字滤波器的时延量为Δt=t2-t1=5s。
|
| 图 5 Heave信号滤波前后时延对比图 Figure 5 The time delay comparison between Heave signal before and after being filtered |
|
| 图 6 Heave信号滤波后时延消除 Figure 6 The time delay elimination of filtered Heave signal |
同理,当滤波器阶数分别为60、80时,FIR高通数字滤波器也会产生相应时延(图 7~8)。
|
| 图 7 滤波后时延图(N=60) Figure 7 The time delay after being filtered (N=60) |

|
| 图 8 滤波后时延图(N=80) Figure 8 The time delay after being filtered (N=80) |
表 1列出了当阶数分别为20、40、60、80、100时,滤波后Heave信号产生的时延量。
| 阶数 | 20 | 40 | 60 | 80 | 100 |
| 时延量/s | 2.5 | 5 | 7.5 | 10 | 12.5 |
表 1数据表明,FIR数字滤波器产生的时延量随着阶数的增加而增大。不难发现,在上述不同阶数下,由时延模型计算出的滤波后信号时延量,与表 1中的时延量是完全一致的,从而也进一步验证了文中消除FIR滤波器时延模型的正确性。
如果将滤波后得到的输出序列通过向前平移对应的延迟时间量,则滤波处理后的信号能够与滤波前的信号保持严格的时间上的同步,这为信号后期融合奠定了基础。
综合考虑信号滤波后的效果和计算的复杂程度,本文选取阶数为60的FIR高通数字滤波器,其滤波结果如图 9所示。
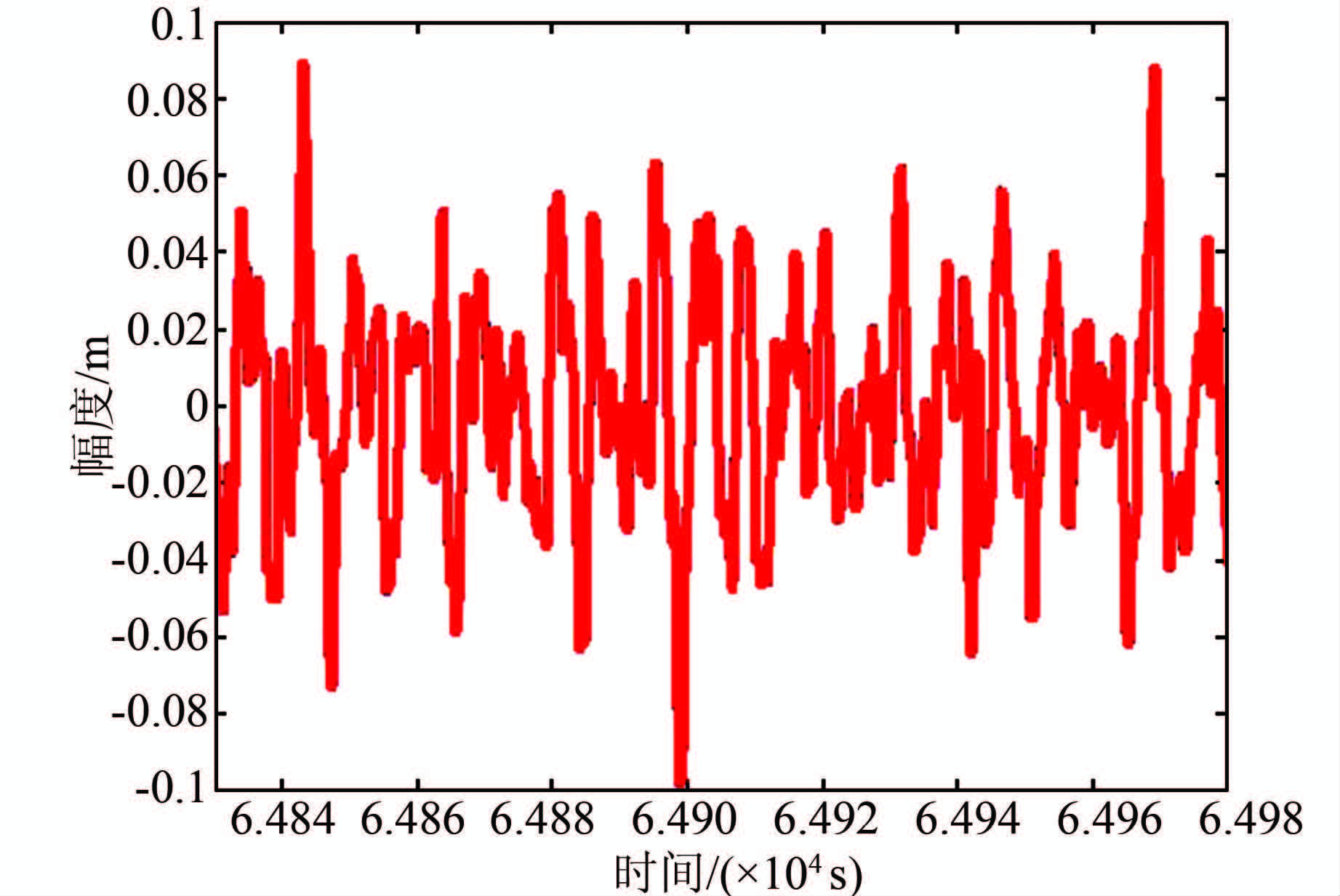
|
| 图 9 滤波后的Heave信号 Figure 9 The filtered Heave signal |
为进一步验证论文所给出的时延消除方法的性能,下面与其他常用方法进行对比分析。考虑到现有关于FIR滤波器时延的解决方法多是根据实际应用领域和具体信号的特点,有针对性地去消除时延,通常不具一般意义上的适用性。而相比其他现有方法,文献[10]所提出的方法在消除时延方面可以达到较好的效果,其基本思想是先对原始信号进行波形匹配,得到一组已延拓的信号,然后进行FIR滤波,提取与原始信号数据长度一致的滤波后端信号即可。为验证本文与文献[10]的时延消除效果,利用本文的方法与其进行了对比,发现二者在时延消除效果方面相当,但论文所提算法的运行速度明显加快(如表 2)。究其原因,文献[10]一方面引入了数据延拓等处理,增加了算法的复杂度,另一方面延拓后有时会难以保证延拓数据的正确性,尤其是在信号变化复杂呈现无规律的情况下,进而会影响滤波效果。在对信号处理实时性要求较高的实际应用中,本文方法将会表现出更加明显的优越性。
| 方法 | 本文方法 | 其他方法 |
| 运行时间/s | 0.008 5 | 0.032 8 |
图 10为与前文Heave信号对应时刻的GPS高程信号时域图,采样频率fs2=1 Hz。要提取出中、长周期的有效信号,需要利用FIR低通数字滤波器进行滤波。
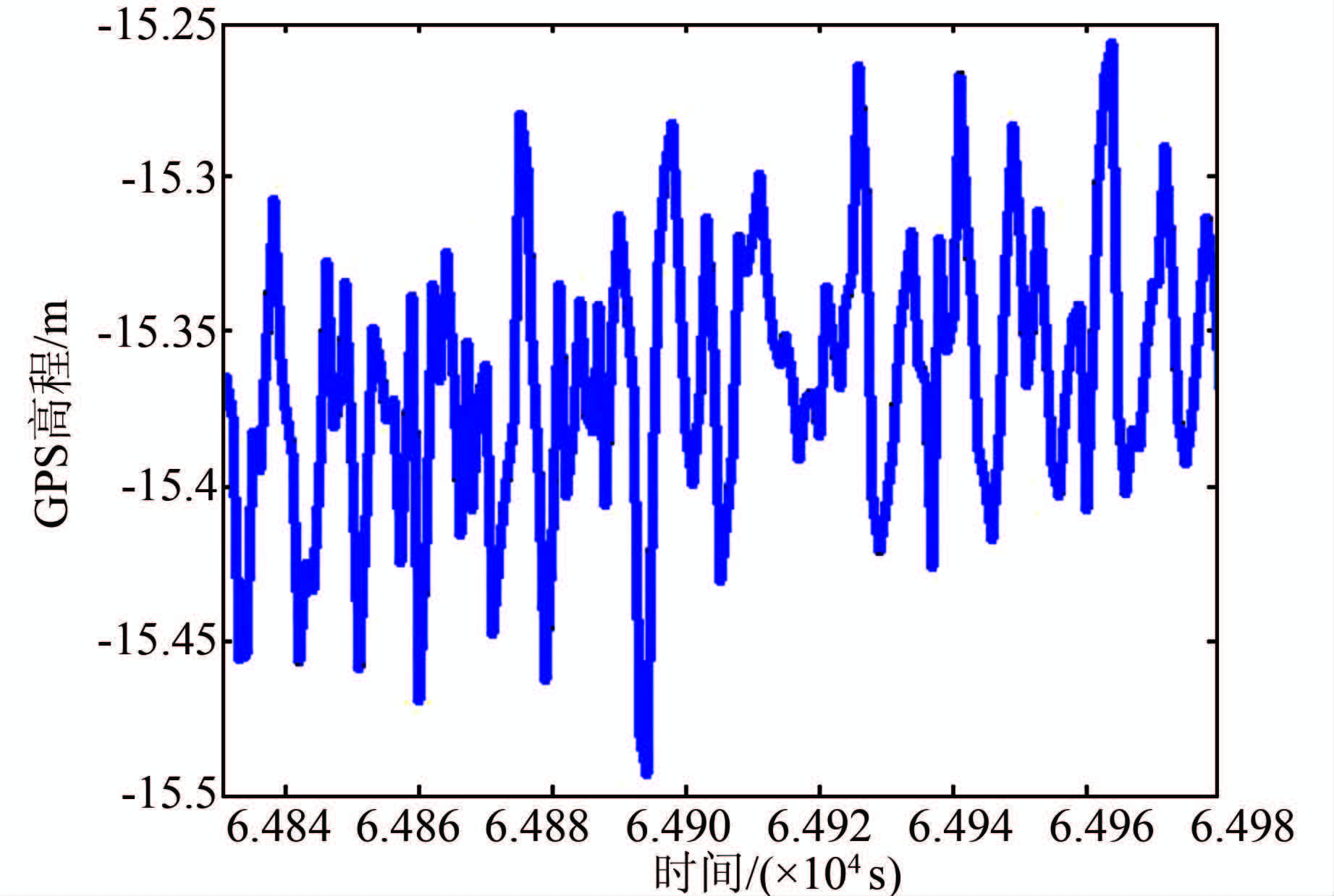
|
| 图 10 原始GPS高程信号 Figure 10 The original GPS signal |
FIR低通数字滤波器的截止周期及阶数选取与前述高通滤波器的参数相同,采用前述给出的模型消除时延,得到滤波后的GPS高程信号如图 11所示。
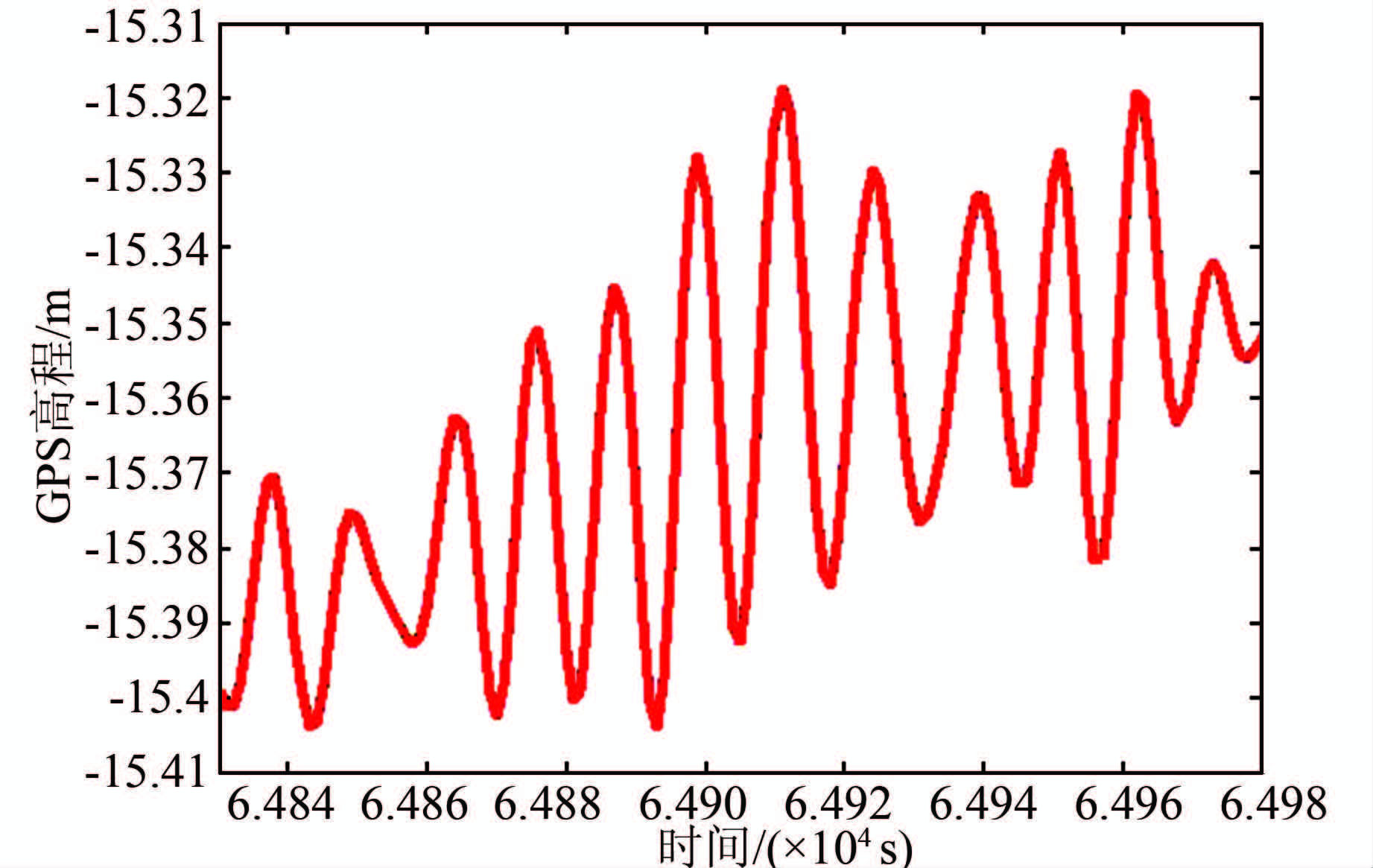
|
| 图 11 滤波后GPS高程信号 Figure 11 The filtered GPS height signal |
滤波后的GPS高程信号已经滤除了高频的干扰信息,整个数据显得更加平滑,而且消除了传统FIR数字滤波器存在的时延问题,滤波效果显著。
3 信号融合获得高频Heave信号和中、低频GPS高程信号后,需要对这两个信号进行数据融合处理。由于这两个信号的采样频率存在差异,融合前需要进行进一步的处理。通过插值算法可以将采样频率较低的GPS信号投射到Heave信号的时间刻度上,使插值后的GPS信号与Heave信号时间刻度严格对齐。为保证插值质量,本文选用了三次样条插值算法[15]。
经过上述处理后,便可直接进行Heave信号和GPS高程信号的有机融合。图 12为融合后的信号波形,融合后的信号不但含有GPS高程信号中的中低频信号,又含有Heave信号中的高频成分,因而融合后所得到的全频段信号能真实地反映换能器瞬时垂直运动,克服了传统数据处理模式的弊端。
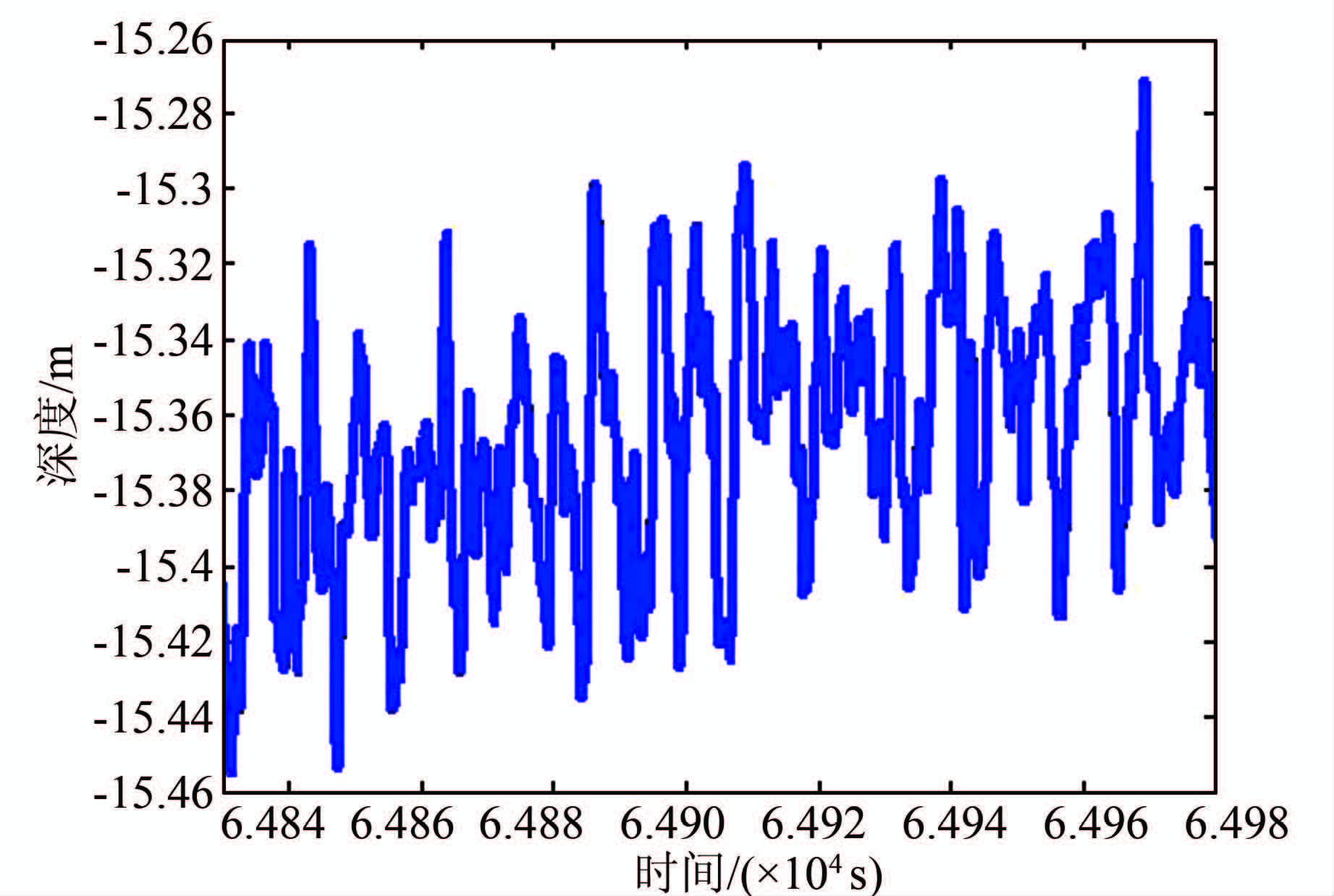
|
| 图 12 融合后的信号 Figure 12 The signal after fusion |
本文从理论上分析和推导了FIR数字滤波器产生时延的原因,给出了消除滤波器时延的数学模型。将该模型应用到多波束测深系统对Heave信号和GPS高程信号的处理中,合成了可以正确反映换能器瞬时垂直运动的全频段信号,克服了传统方法所产生的频段遗漏问题,并彻底消除了滤波后信号的时延影响。
此外,本文从滤波后的信号波形直接分析时延的影响,得到了与模型计算完全一致的时延量,从而更进一步验证了模型的正确性。本文提出的消除FIR数字滤波器时延的方法,实际应用中具有普遍的参考价值。
| [1] |
沈希忠.
数字信号处理[M]. 北京: 机械工业出版社, 2014.
Shen Xizhong. Digital Signal Processing[M]. Bejing: China Machine Press, 2014. |
| [2] | Mitra S K, Kuo Y. Digital Signal Processing: A Computer-based Approach[M]. New York: McGraw-Hill, 2006. |
| [3] |
孙耀奇, 高火涛, 熊超, 等. 基于Matlab和FPGA的FIR数字滤波器设计及实现[J].
现代电子技, 2008, 31(11): 89–92.
Sun Yaoqi, Gao Huotao, Xiong Chao, et al. Design and implementation of FIR digital filter based on Matlab and FPGA[J]. Modern Electronics Technique, 2008, 31(11): 89–92. |
| [4] |
郭广浩, 刘志哲, 孟庆龙, 等. 多级并行流水FIR数字滤波器的设计与验证[J].
现代电子技术, 2015(1): 69–72.
Guo Guanghao, Liu Zhizhe, Meng Qinglong, et al. Design and verification of multilevel parallel pipeline FIR digital filter[J]. Modern Electronics Technique, 2015(1): 69–72. |
| [5] |
张晓文, 王江宏. LTE中变速率FIR滤波器的FPGA实现[J].
通信技术, 2010(02): 207–209.
Zhang Xiaowen, Wang Jianghong. FPGA implementation of fractional rate FIR filter in LTE[J]. Communications Technology, 2010(02): 207–209. |
| [6] |
黄桂根, 高梅国, 陶青长, 等. 线性调频信号在部分相关情况下的数字脉冲压缩分析[J].
信号处理, 2005(4): 483–486.
Huang Guigen, Gao Meiguo, Tao Qingchang, et al. Analysis on partial correlation digital pulse compression of LFM signal[J]. Signal Processing, 2005(4): 483–486. |
| [7] |
杨宣兵, 陈进, 项胜, 等. 基于 TMS320F28335 的感应无线数据通信器设计[J].
电工技术学报, 2013, 28(Supplement 2): 189–193.
Yang Xuanbing, Chen Jin, Xiang Sheng, et al. Design of data transmission system by induction radio based on TMS320F28335[J]. Transactions of China Electrotechnical Society, 2013, 28(Supplement 2): 189–193. |
| [8] |
程耀强, 徐德民, 万彦辉, 等. 激光陀螺动态特性研究 (二)[J].
上海交通大学学报, 2012, 46(8): 1274–1279.
Cheng Yaoqiang, Xu Demin, Wan Yanhui, et al. Research on the dynamic characteristics of laser gyroscope(Part Two)[J]. Journal of Shanghai Jiaotong University, 2012, 46(8): 1274–1279. |
| [9] |
王林, 何俊, 李芳, 等. 用于探测极低频信号的光纤传感器相位生成载波解调方法[J].
中国激光, 2011, 38(4): 0405001-1–0405001-7.
Wang Lin, He Jun, Li Fang, et al. Ultra low frequency phase generated carrier demodulation technique for fiber sensors[J]. Chinese Journal of Lasers, 2011, 38(4): 0405001-1–0405001-7. |
| [10] |
伏燕军, 程强强, 于润桥, 等. 信号FIR数字滤波后相位延迟的消除[J].
计算机工程与应用, 2012, 48(7): 146–149.
Fu Yanjun, Cheng Qiangqiang, Yu Runqiao, et al. Eleminating the phase delay of the FIR filtered signal[J]. Computer Engineering and Application, 2012, 48(7): 146–149. |
| [11] |
李琦, 杨幸芳, 刘丁. 一种 2FSK 解调算法的 DSP 实现[J].
现代电子技术, 2004, 27(3): 84–86.
Li Qi, Yang Xingfang, Liu Ding. A DSP implementation of 2FSK demodulation algorithm[J]. Modern Electronics Technique, 2004, 27(3): 84–86. |
| [12] |
唐树元, 王云杉, 张涛. 一种适用于微纳卫星通信系统的数字下变频算法[J].
电子技术应用, 2011, 37(10): 99–102.
Tang Shuyuan, Wang Yunshan, Zhang Tao. A DDC algorithm for nicro/nano satellite communication system[J]. Application of Electronic Technique, 2011, 37(10): 99–102. |
| [13] |
暴景阳, 刘雁春. 海道测量水位控制方法研究[J].
测绘科学, 2006, 31(6): 49–51.
Bao Jingyang, Liu Yanchun. Research on the method of hydrographic water level control[J]. Science of Surveying and Mapping, 2006, 31(6): 49–51. |
| [14] | Zhang H, Zhao J, Bai X. Design of optimum filter for blend of GPS height and heave[C]//Electronic Measurement & Instruments, 2009. ICEMI'09. 9th International Conference on, IEEE, 2009: 3-218-3-222. |
| [15] |
颜庆津.
数值分析[M]. 北京: 北京航空航天大学出版社, 2012.
Yan Qingjin. Numerical Analysis[M]. Beijing: Beihang University Press, 2012. |
 2016, Vol. 49
2016, Vol. 49



