武汉大学学报(工学版)   2016, Vol. 49 Issue (1): 22-26

文章信息

程井, 张枝阳, 李同春
CHENG Jing, ZHANG Zhiyang, LI Tongchun
基于无单元伽辽金法的混凝土通水温度计算
Temperature computation for pipe cooling problems of concrete structures based on EFGM
武汉大学学报(工学版), 2016, 49(1): 22-26
Engineering Journal of Wuhan University, 2016, 49(1): 22-26
http://dx.doi.org/10.14188/j.1671-8844.2016-01-004

文章历史

收稿日期: 2015-05-09
 Abstract              PDF               Figures               Tables
引用本文 0
程井, 张枝阳, 李同春. 基于无单元伽辽金法的混凝土通水温度计算[J]. 武汉大学学报(工学版), 2016, 49(1): 22-26.
CHENG Jing, ZHANG Zhiyang, LI Tongchun. Temperature computation for pipe cooling problems of concrete structures based on EFGM[J]. Engineering Journal of Wuhan University, 2016, 49(1): 22-26.
基于无单元伽辽金法的混凝土通水温度计算
程井1,2, 张枝阳2, 李同春2     
1. 武汉大学水资源与水电工程科学国家重点实验室,湖北 武汉 430072;
 2. 河海大学水利水电学院，江苏 南京 210098
收稿日期: 2015-05-09
作者简介: 程井(1982-)，男，副教授，主要从事高坝结构数值仿真方面的研究，E-mail:cj042@126.com.
基金项目: 水资源与水电工程科学国家重点实验室开放基金(编号：2012B103);国家自然科学基金青年基金(编号：51009056);教育部博士点新教师基金(编号：20100094120005).
摘要: 利用无单元伽辽金法的高精度优势，探讨研究其在大体积混凝土智能通水及精准温控中的应用.首先将大体积混凝土通水冷却问题近似为轴对称热传导问题，使用二维背景网格来离散对称截面，提出了基于无单元伽辽金法的基本理论及数值计算过程；当不考虑沿程水温变化时，问题进一步简化为轴对称平面问题，并给出了相应的计算公式；对于典型二期通水冷却问题，建立了不同密度的背景网格模型并进行了计算分析，结果显示无单元伽辽金法在求解这种问题时具有良好收敛性，且采用相同节点时计算精度明显高于有限元法.进一步的工程应用则还需开展三维问题沿程水温模拟及无单元伽辽金法与有限元法的耦合等研究.
关键词： 无单元伽辽金法     大体积混凝土     通水冷却     热传导     轴对称问题    
Temperature computation for pipe cooling problems of concrete structures based on EFGM
CHENG Jing1,2, ZHANG Zhiyang2, LI Tongchun2     
1. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China;
 2. College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210098, China
Abstract: The high-accuracy element-free Galerkin method (EFGM) is applied to the intelligent pipe cooling and fine temperature control of mass concrete. The pipe-cooling of mass concrete is first defined as axisymmetric heat conduction problem; approximately; and then the 2D background meshes are used to discretize the symmetric section. The equation deduction and numerical approach based on EFGM are proposed. For cases where the water keeps constant along the pipe, the problem can be simplified as an axisymmetric plane problem; and corresponding equations are also given. To investigate the performance of the approach, different background meshes are built for analyzing a typical second-stage pipe cooling problem; the obtained results show that the EFGM has good convergence and higher accuracy than FEM. Further researches on water temperature rising along the pipes for 3D problems and the coupling of FEM with EFGM are needed to promote practical engineering.
Key words: element-free Galerkin method (EFGM)     mass concrete     pipe cooling     heat conduction     axisymmetric problem.    

对于大型复杂水利工程及土木工程，数值仿真时往往需要同时模拟整体结构及细部构造，这将耗费大量计算成本.传统有限元方法依托单元进行插值和积分，在模拟不连续问题(如断裂问题)、多尺度问题以及大变形问题时，需要不断重新划分网格且有可能发生网格畸变，给计算带来不便.为此学者们提出了多种无网格方法，具体包括光滑质点流体动力学方法(SPH)[1]、重构核点法(RKPM)、无单元伽辽金法(EFGM)[2]、局部彼得洛夫-伽辽金无网格法(MLPG)[3]、无网格粒子法[4]、光滑有限元法(SFEM)[5]等.在这些方法中，无单元伽辽金法已被广泛应用于二维和三维断裂问题，以及其他类型的物理场如温度场和渗流场问题.当节点数相同时，无单元伽辽金法的刚度矩阵带宽比有限元法大、计算时间长，但其计算精度远高于有限元法，同时在模拟裂纹时，不需要改变背景网格，而只需在裂缝尖端附近增加节点即可.

近期无单元伽辽金法已成功应用于水工大体积混凝土结构的温控仿真分析，具体包括稳态温度场、施工期瞬态温度场和温度应力的仿真计算[6, 7]，以及温度裂纹的模拟及其扩展分析[8].近年来大体积混凝土温控防裂技术在时空控制、测温预报、温度场重构及智能控制方法等方面发展迅速[9-10]，然而对于施工期关键智能控制技术(通水冷却效果的快速高精度模拟)仍未得到很好的解决.本文研究无单元法在通水冷却问题中的精细模拟，以推动其在大体积混凝土智能通水及精准温控中的应用.首先将通水冷却问题近似等效为内置水管的混凝土圆柱体，从而简化为轴对称问题并使用无单元伽辽金法进行求解；当水管长度不大或水温沿程上升不明显时，问题可进一步简化为轴对称平面问题.最后通过典型算例对无单元法进行了验证.

1 移动最小二乘近似

无单元伽辽金法采用移动最小二乘近似(moving least square)插值函数来构建形函数.首先，计算域被离散为一系列规则或不规则分布的节点.对于计算域内的连续场函数u(x)，如固体力学问题的位移场或热传导问题中的温度场，在某点x0附近的场函数可以近似如下：

$u\left( x \right)\approx {{u}^{h}}(x,{{x}_{0}})=\sum\limits_{j}^{m}{{{p}_{j}}}\left( x \right){{a}_{j}}(x,{{x}_{0}})={{p}^{T}}\left( x \right)a({{x}_{0}})$    (1)

基于移动最小二乘近似，可得到如下形函数：

$N(x,{{x}_{0}})={{p}^{\text{T}}}(x){{A}^{-1}}({{x}_{0}})B({{x}_{0}})$    (2)

关于形函数的详细推导见文献[2].本文采用线性基函数，且节点I的影响域半径计算公式如下：

${{d}_{\text{I}}}=1.5\times {{c}_{\text{I}}}$    (3)

式中：cI为以点I为圆心并包含12个节点的圆域半径.

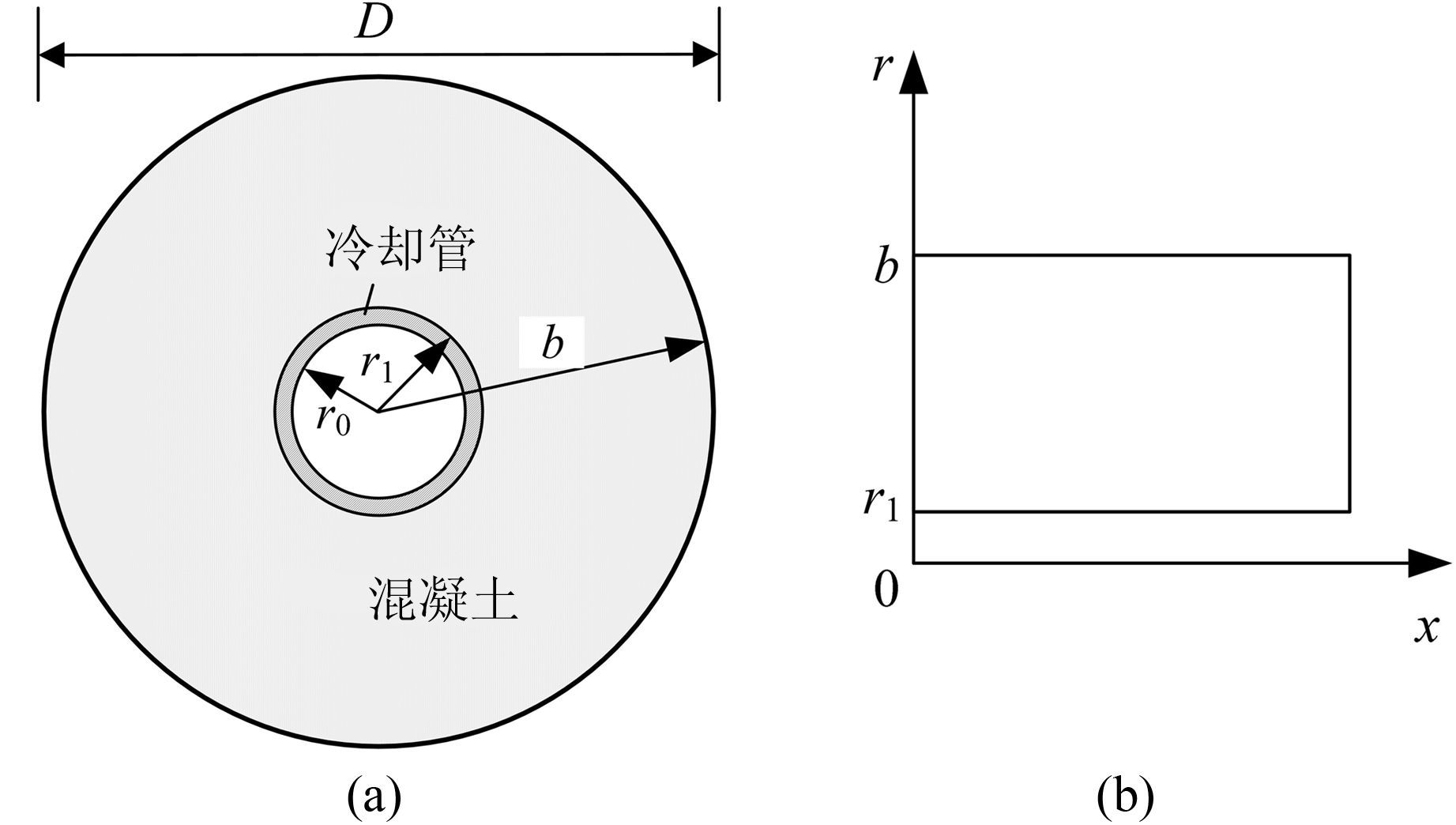
2 轴对称热传导问题的变分形式

大体积混凝土内部冷却水管在铅直断面上通常采用梅花形或矩形布置，单根冷却水管影响范围可近似为一空心混凝土圆柱体[11],如图 1(a)所示，混凝土柱内外半径分别为r1和b，r0为水管内径.假定混凝土圆柱体的温度沿环向分布均匀，则仅有沿径向r和轴向x的温度梯度，此时三维问题退化为轴对称问题，其对称截面如图 1(b)所示.

图 1 埋入水管的混凝土块图解 Figure 1 Sketch of the concrete block embedded with cooling pipe
图选项
2.1 控制方程

轴对称热传导问题的控制偏微分方程如下[12]：

$c\rho \frac{\partial T}{\partial t}=\lambda \left( \frac{{{\partial }^{2}}T}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}T}{\partial {{r}^{2}}}+\frac{1}{r}\frac{\partial T}{\partial r} \right)+c\rho \frac{\partial \theta }{\partial t}$    (4)

其中：x为对称轴方向；r为径向；λ、c、ρ和θ分别为混凝土的导热系数、比热、密度以及绝热温升.

初始条件及边界条件如下：

$\left\{ \begin{matrix} T={{T}_{0}}(x,r)\text{ ,} & t\text{=0}时的初始温度 \\ T={{T}_{b}}(x,r,t), & 已知温度边界{{\Gamma }_{1}} \\ \lambda \frac{\partial T}{\partial n}=-q, & 已知热流边界{{\Gamma }_{2}} \\ \lambda \frac{\partial T}{\partial n}=-\beta (T-{{T}_{a}}), & 对流边界{{\Gamma }_{3}} \\ \end{matrix} \right.$    (5)

其中，β及Ta分别为表面放热系数及介质温度.

2.2 稳态热传导问题

对于稳态问题，混凝土发热已经完成，温度分布基本恒定：

$\frac{\partial \theta }{\partial t}=0\text{,}\frac{\partial T}{\partial t}=0$    (6)

将式(6)代入式(4)，得到稳态问题的控制方程：

$\frac{{{\partial }^{2}}T}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}T}{\partial {{r}^{2}}}+\frac{1}{r}\frac{\partial T}{\partial r}=0$    (7)

使用加权余量法和伽辽金权重法，等式具有以下弱形式：

$-\int_{\Omega }{\lambda r\left[ {{\left( \frac{\partial N}{\partial x} \right)}^{\text{T}}}\frac{\partial N}{\partial x}+ \right.}\left. {{\left( \frac{\partial N}{\partial r} \right)}^{\text{T}}}\frac{\partial N}{\partial r} \right]u\text{d}\Omega +\int_{{{\Gamma }_{3}}}{r{{N}^{\text{T}}}\beta ({{T}_{a}}-Nu)\text{d}\Gamma }=0$    (8)

式中，N是引进的移动最小二乘形函数.式(8)可以写成以下的矩阵形式：

$Ku=P$    (9)

其中:

$\text{ }\left\{ \text{ }\begin{matrix} K={{K}_{k}}+{{K}_{c}}\text{; }{{K}_{c}}=\int_{{{\Gamma }_{c}}}{r\beta {{N}^{\text{T}}}N\text{d}\Gamma }\text{;} \\ {{K}_{k}}=\int_{\Omega }{\lambda r\left[ {{\left( \frac{\partial N}{\partial x} \right)}^{\text{T}}}\frac{\partial N}{\partial x}+ \right.}\left. {{\left( \frac{\partial N}{\partial r} \right)}^{\text{T}}}\frac{\partial N}{\partial r} \right]\text{d}\Omega \\ P={{P}_{c}}=\int_{{{\Gamma }_{c}}}{r{{N}^{\text{T}}}\beta {{T}_{a}}\text{d}\Gamma } \\ \end{matrix} \right.$    (10)

式中：Kk为热传导矩阵；Kc为对流边界附加热传导矩阵；Pc为对流表面热流量；u为节点温度列阵.

2.3 瞬态热传导问题

使用加权余量法、伽辽金权重法和时间差分近似时，式(4)、(5)具有以下的等价矩阵形式：

$C\dot{u}+Ku=P$    (11)

式中：C为热容矩阵；是$\dot{u}$对时间的导数；K、u及P物理意义同上；P包含内容不同.

$\left\{ \begin{matrix} C=\int_{\Omega }{r\rho c{{N}^{\text{T}}}N\text{d}\Omega } \\ P={{P}_{c}}+{{P}_{h}} \\ {{P}_{h}}=\int_{\Omega }{r\rho c\frac{\partial \theta }{\partial t}{{N}^{\text{T}}}d\Omega } \\ \end{matrix} \right.$    (12)

应用两点循环公式来离散时间域时，在时段(tn,tn+1)内可获得如下加权余量格式：

$(C/\Delta t+K\varphi ){{u}_{n+1}}+[-C/\Delta t+K(1-\phi )]{{u}_{n}}=\bar{P}$    (13)
$\bar{P}={{P}_{n}}(1-\phi )+{{P}_{n+1}}\phi $    (14)

其中：un及un+1为时段始末节点温度序列；Pn及Pn+1为时段始末荷载序列；Δt为时间间隔；φ为差分系数.φ=1时即得到后差分近似，然后可得式(13)的解：

$(C/\Delta t+K){{u}_{n+1}}={{P}_{n+1}}+(C/\Delta t){{u}_{n}}$    (15)

使用高斯积分法可以计算出式(10)、(12)中的矩阵和列阵.本文网格积分时采用9个高斯点，边界积分时采用2个高斯点.

3 轴对称平面热传导问题的变分形式 3.1 控制方程

当水管长度较小可忽略水管沿程水温的变化时，∂T/∂x=0，通水冷却问题退化为平面问题，此时其控制偏微分方程由式(4)退化为

$c\rho \frac{\partial T}{\partial t}=\lambda \left( \frac{{{\partial }^{2}}T}{\partial {{r}^{2}}}+\frac{1}{r}\frac{\partial T}{\partial r} \right)+c\rho \frac{\partial \theta }{\partial t}$    (16)
3.2 稳态热传导问题

对于稳态问题，采用与2.2节类似的推导可得到如下矩阵形式的控制方程：

$Ku=P$    (17)

其中：

$\left\{ \begin{matrix} K={{K}_{k}}+{{K}_{c}}\text{;}{{K}_{c}}={{r}_{c}}\beta {{N}^{\text{T}}}N \\ {{K}_{k}}=\int_{{{r}_{1}}}^{b}{\lambda r\left[ \left. {{\left( \frac{\partial N}{\partial r} \right)}^{T}}\frac{\partial N}{\partial r} \right] \right.}dr \\ P={{P}_{c}}={{r}_{c}}{{N}^{\text{T}}}\beta {{T}_{a}} \\ \end{matrix} \right.$    (18)

式中：rc为对流边界点处的r坐标.

3.3 瞬态热传导问题

对于瞬态轴对称平面热传导问题，采用与2.3节类似推导，可得如下等价矩阵形式：

$C\dot{u}+Ku=P$    (19)

其中：K、u及P物理意义同前，但P包含内容不同：

$\left\{ \begin{matrix} C=\int_{{{r}_{1}}}^{b}{r\rho c{{N}^{\text{T}}}N}\text{d}r \\ P={{P}_{c}}+{{P}_{h}} \\ {{P}_{h}}=\int_{{{r}_{1}}}^{b}{r\rho c\frac{\partial \theta }{\partial t}{{N}^{\text{T}}}}\text{d}r \\ \end{matrix} \right.$    (20)
4 轴对称问题数值算例

取如图 1(a)所示的内置高密度聚乙烯(HDPE)水管的标准混凝土柱，柱体模型及材料参数为r0=0.013 5 m，r1=0.016 m，b=1.6 m;混凝土参数：λ=208.8 kJ/(m·d·℃),c=0.87 kJ/(kg·℃),ρ=2 400 kg/m3;导温系数a=0.1/ (m2·d);高密度聚乙烯水管导热系数λp=39.84 kJ/(m·d·℃);混凝土初始平均温度Tp=30 ℃；混凝土外表面为绝热边界，内表面通水冷却，冷却水温度Tw=10 ℃.

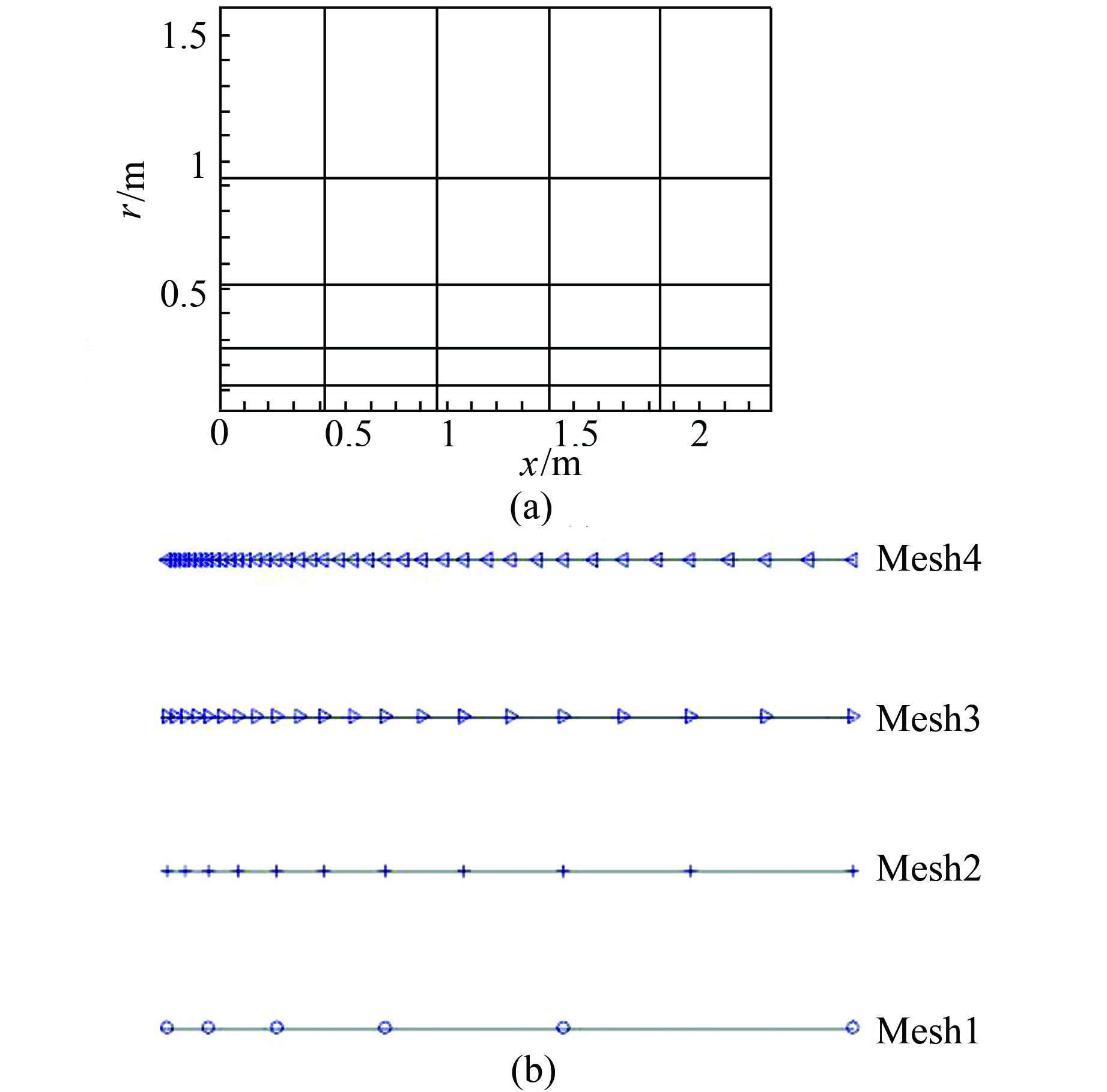
朱伯芳通过分离变量法给出了该问题二期冷却温度场的理论解[11]，本文数值计算时采用4种不同的二维背景网格模型Mesh1-Mesh4，其中Mesh1的背景网格如图 2(a)所示，不同网格模型沿径向的网格密度如图 2(b)所示，其中Mesh1六排节点的径

图 2 不同网格模型沿径向节点分布 Figure 2 Mesh models along radial direction
图选项

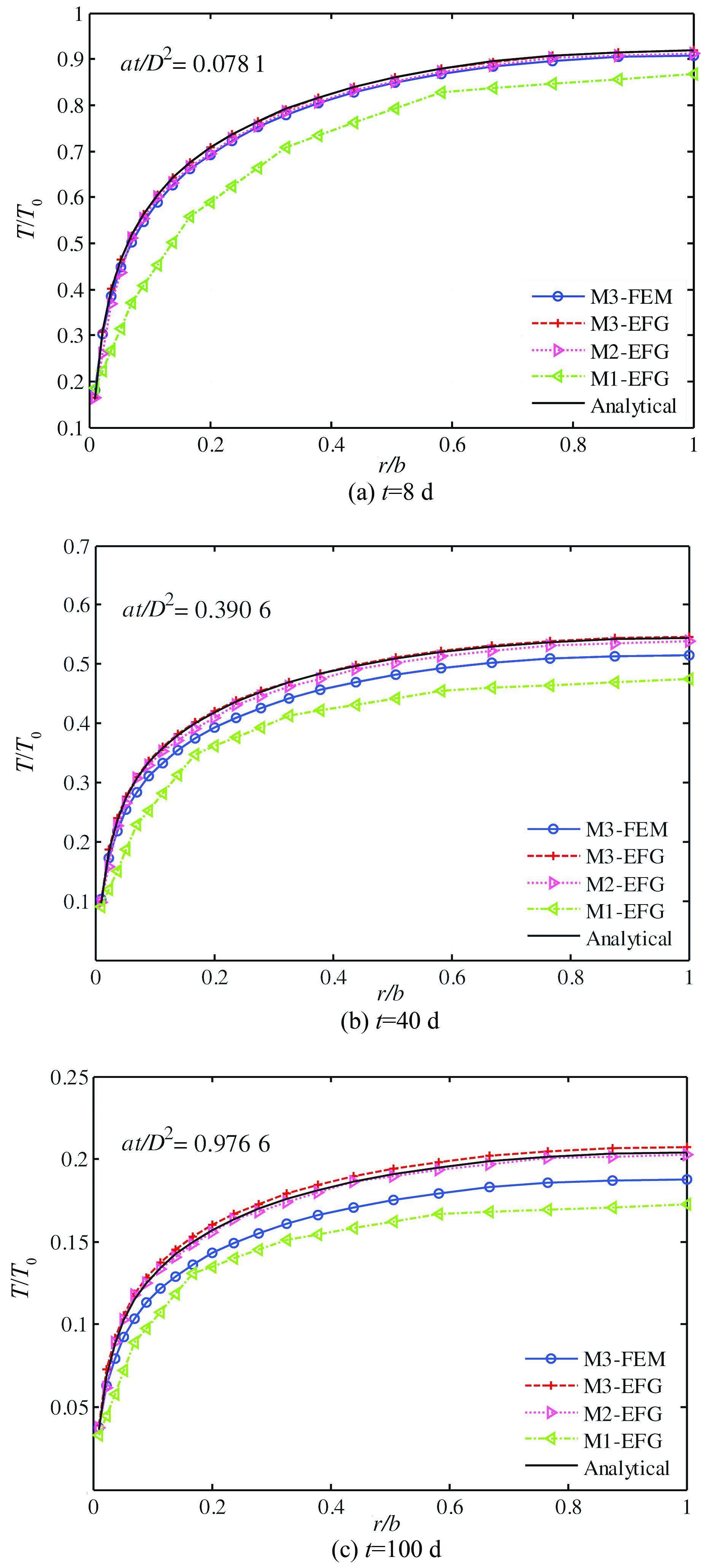
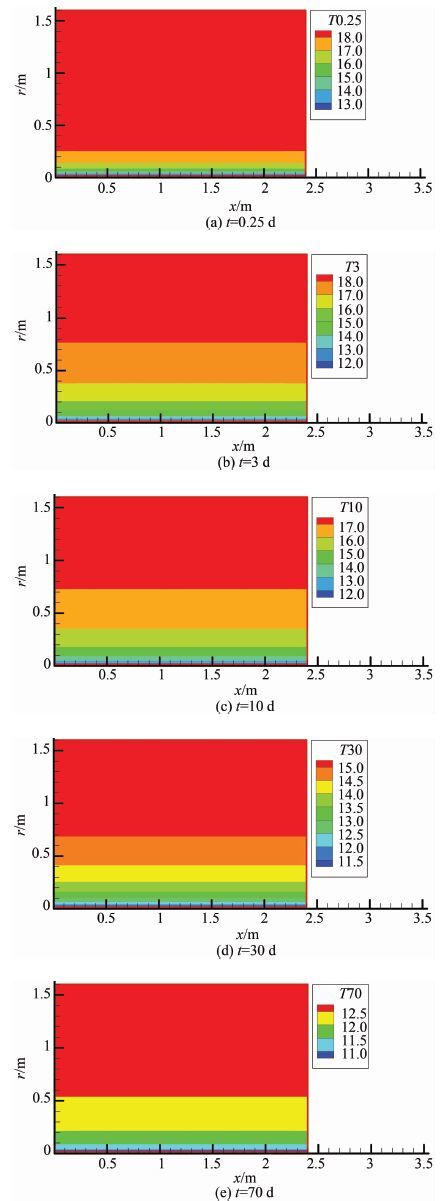
向坐标分别为rx/b=0.01，0.070，0.167，0.326，0.583，1.不同时刻的径向温度分布见图 3，为便于对比，采用归一化后的温度T/T0、径向坐标r/b及时间at/D2，其中T0=Tp-Tw;T=Tt-Tw，Tt为t时刻的混凝土温度.为便于对比，图 3还给出了基于Mesh3的传统有限元法计算结果以及朱伯芳给出的解析解，分别记为‘M3-FEM’及‘Analytical’.图 4给出了在不同时刻的温度等值线云图.

图 3 不同时刻圆柱体轴向温度分布 Figure 3 Temperature along the axis at different times
图选项
图 4 对称截面不同时刻的温度等值线云图 Figure 4 Temperature contour maps for section at different times
图选项

由计算结果可知：

1) 当背景网格加密时，无单元法计算结果逐渐趋近解析解，这证明了无单元伽辽金法的收敛性和稳定性.

2) 对于一个特定的网格模型如Mesh3，无单元法结果比有限元法结果精确得多.这是因为无单元伽辽金法使用移动最小二乘近似，它能提供更高次的形函数，因此更适合于模拟水管周边的高温度梯度.

3) 虽然Mesh2密度远小于Mesh3，但其无单元计算结果仍然比Mesh3的有限元法结果精确得多.

5 结论

本文提出了大体积混凝土水管冷却问题的无单元伽辽金法计算模型，给出了基于轴对称瞬态热传导问题的水管冷却基本理论以及数值计算过程；采用典型混凝土柱体二期通水冷却实例，对计算模型进行了验证.结果表明，基于无单元伽辽金法的计算模型具有很好的收敛性，且在冷却水管周围布设较少的节点即可达到较高的精度.这为大体积混凝土智能温控及精准温控提供了重要计算工具.

无单元伽辽金法在计算精度、裂纹模拟方面具有显著优势，但要将其应用于实际工程还需开展三维问题中沿程水温的模拟、无单元伽辽金法与有限元法的耦合等方面的后续研究.

参考文献
[1] Monaghan J J. Smoothed particle hydrodynamics[J]. Annual Review of Astronomy and Astrophysics, 1992, 30: 543–574. DOI:10.1146/annurev.aa.30.090192.002551
[2] Belytschko T, Lu Y Y, Gu L. Element-free Galerkin methods[J]. International Journal for Numerical Methods in Engineering, 1994, 37(2): 229–256. DOI:10.1002/(ISSN)1097-0207
[3] Atluri S N, Zhu T. A new meshless local Petrov-Galerkin (MLPG) approach in computational mechanics[J]. Computational Mechanics, 1998, 22(2): 117–127. DOI:10.1007/s004660050346
[4] Belytschko T, Krongauz Y, Dolbow J, Gerlach C. On the completeness of meshfree particle methods[J]. International Journal for Numerical Methods in Engineering, 1998, 43(5): 785–819. DOI:10.1002/(ISSN)1097-0207
[5] Cheng Jing, Liu G R, Li Tongchun, Wu Shengchuan, Zhang Guiyong. ES-PIM with cell death and birth technique for simulating heat transfer in the concrete dam construction process[J]. ASCE-Journal of Engineering Mechanics, 2012, 138(1): 133–142. DOI:10.1061/(ASCE)EM.1943-7889.0000312
[6] 程井, 常晓林, 周伟, 等. 应用无单元伽辽金法计算大坝稳定温度场[J]. 武汉大学学报(工学版), 2008, 41(4): 48–51.
Cheng Jing, Chang Xiaolin, Zhou Wei, et al. Application of element-free Galerkin method to computation of steady temperature field for dams[J]. Engineering Journal of Wuhan University, 2008, 41(4): 48–51.
[7] Cheng J, Zhu Y M, Chang X L. Application of element-free Galerkin method on the steady-state and transient temperature field simulation for high concrete dams[C]//3rd Asia-Pacific International Conference on Computational Methods in Engineering. Nanjing: ICOME 2009.
[8] 程井, 常晓林, 周伟, 等. 基于无单元伽辽金法的水工结构温度应力及温度裂纹扩展计算[J]. 四川大学学报(工程科学版), 2009(4): 26–30.
Cheng Jing, Chang Xiaolin, Zhou Wei, et al. Simulation of thermal stress and crack propagation in hydraulic structures based on EFGM[J]. Journal of Sichuan University (Engineering Science Edition), 2009(4): 26–30.
[9] 黄达海, 陈彦玉, 王祥峰, 等. 基于分布式光纤测温的特高拱坝温控预报研究[J]. 水利水电技术, 2010(9): 42–46.
Huang Dahai, Chen Yanyu, Wang Xiangfeng, et al. Study on prediction of temperature control of super-high concrete arch dam with fiber-optic-based distributed temperature sensing[J]. Water Resources and Hydropower Engineering, 2010(9): 42–46.
[10] 林鹏, 李庆斌, 周绍武, 等. 大体积混凝土通水冷却智能温度控制方法与系统[J]. 水利学报, 2013(8): 950–957.
Lin Peng, Li Qingbin, Zhou Shaowu, et al. Intelligent cooling control method and system for mass concrete[J]. Journal of Hydraulic Engineering, 2013(8): 950–957.
[11] 朱伯芳. 大体积混凝土温度应力与温度控制[M]. 北京: 中国电力出版社, 2003.
Zhu Bofang. Thermal Stresses and Temperature Control of Mass Concrete[M]. Beijing: China Water & Power Press, 2003.
[12] 孔祥谦. 热应力有限单元法分析[M]. 上海: 上海交通大学出版社, 1999.
Kong Xiangqian. Finite Element Analysis of Thermal Stress[M]. Shanghai: Shanghai Jiaotong University Press, 1999.