文章信息
- 邓嘉辉, 周惠成, 李一冰
- DENG Jiahui, ZHOU Huicheng, LI Yibing
- 阶梯水价的居民节水效益及水费支出的测算
- Research on the calculating of residents' water-saving effect and water fee expenditure under increasing block water price
- 武汉大学学报(工学版), 2019, 52(2): 116-124
- Engineering Journal of Wuhan University, 2019, 52(2): 116-124
- http://dx.doi.org/10.14188/j.1671-8844.2019-02-003
-
文章历史
- 收稿日期: 2017-10-29
对居民生活用水实施阶梯水价,它作为一种经济手段和提价方式,在国际上被公认为是提高居民节水意识与水资源利用率的有效措施.随着我国阶梯水价政策的推广,如何制定阶梯水价、什么样的阶梯水价方案更合理已成为亟待研究和解决的问题.阶梯水价的主要目的是为了节水,但由于经济杠杆的作用,阶梯水价在带来节水效益的同时也会提高居民的水费支出,故在实施阶梯水价前有必要对阶梯水价方案的节水效益和居民水费支出增量进行测算,为阶梯水价方案的合理制定奠定基础.
在阶梯水价节水效益测算方面已有多位学者进行了研究,主要是从ELES扩展线性支出模型和价格弹性2个角度入手.张嵘等[1]、贾国宁等[2]利用ELES扩展性线性支出模型,将不同阶梯上的水量看作独立的不同商品进行分析,模拟了阶梯式水价所产生的节水效果.然而笔者认为ELES扩展线性支出模型中将各个阶梯水量看作是独立商品进行分析的假设存在缺陷.阶梯水价各个阶梯水量存在明显的逻辑关系,只有用满第1阶梯水量的用户才能使用第2阶梯水量,各阶梯水量并不独立,故ELES模型的结果难免失真.由于阶梯水价是通过价格来影响需求,故根据需求价格弹性理论来测算阶梯水价节水效益具有理论上的可行性.在居民用水需求价格弹性研究方面,文献[3-9]分别利用双对数模型定量分析了不同城市或不同区域的居民用水价格弹性、收入弹性等.然而,以上关于用水价格弹性的研究仅限于得出价格弹性值,没有将弹性用于阶梯水价节水效益的测算,究其原因是因为没有考虑阶梯水价对不同用水量用户采取不同收费政策的特性,也就是没有考虑居民用水量的分布情况,故获取居民用水量的分布是使用价格弹性准确计算阶梯水价节水效益的必由之路.此外,居民水费支出也是影响水价合理性的重要因素,潘莉等[10]采用综合评价因子分析法和阶梯水价标准调整动态分析法,对某地区阶梯水价支付能力进行了定量研究,得到了不同水费支付能力的收入标准;柳长顺等[11]运用计量分析的方法分析了华北地区城镇居民人均水费支出占人均可支配收入比例与水费支出占家庭人均消费支出比例,认为应进一步发挥水价的经济杠杆作用,加大水价的调整幅度.
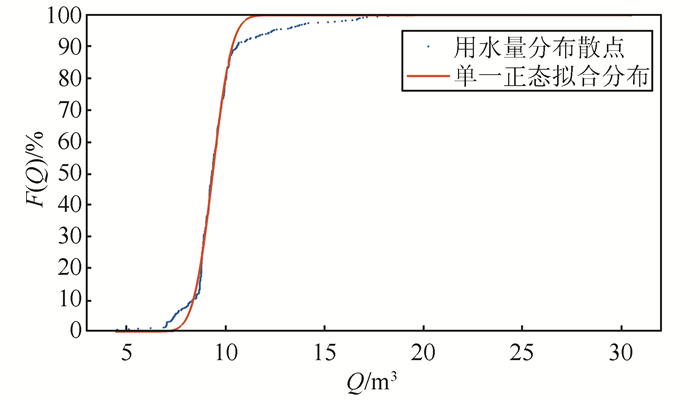
1 居民户月均用水量的分布实施阶梯水价的目的,主要是对用水较多的用户实行经济惩罚,同时适度提高水价,以促进节水.因此,居民用水量多少的识别,即用水量的分布特征是确定合理阶梯水价的基础.本文对大连市10个实现用水监测的典型社区中635户居民2015年月均用水量进行了数据收集,通过拟合这635户居民的用水分布模拟大连市居民的用水分布.首先使用单一正态分布尝试拟合大连市用水分布,得到的分布函数F(Q)如图 1所示,结果显示Q服从正态分布N(9.335, 0.764 92),R2值为0.992 1.但观察图 1可知,7~9 m3和11~13 m3段拟合效果不好,与真实分布相差较大,考虑使用其他分布函数进行尝试.
|
| 图 1 单一正态分布拟合大连市居民用水量的分布函数 Fig. 1 Single normal distribution fits distribution of Dalian's residential water demand |
使用核密度估计[12, 13]对大连市居民用水量数据进行概率密度估计,将得到的经验频率分布结果与单一正态分布拟合得到的概率密度函数f(Q)(f(Q)=F′(Q))进行对比,如图 2所示.

|
| 图 2 单一正态分布拟合的概率密度结果和核密度函数对比 Fig. 2 Contrast of probability density result fitted by single normal distribution and kernel density |
通过观察图 2可以发现大连市居民用水概率密度分布呈现轻微的正偏态,即众数(核密度函数的峰值)小于分布期望值9.335 m3.且7~9 m3和11~13 m3段的核密度函数值较单一正态分布拟合出的分布密度偏高,可见大连市的用水分布难以用单一正态分布来准确拟合,故考虑使用2个正态分布函数按比例叠加的模型进行拟合,2个分布呈相互补偿与相互调节作用,模型如下:
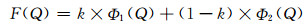 (1)
(1)
式中:Φ1和Φ2均为期望与方差待定的正态分布函数,Φ1的期望与标准差分别为a和b,Φ2的期望与标准差分别为c和d;k为比例调节系数.
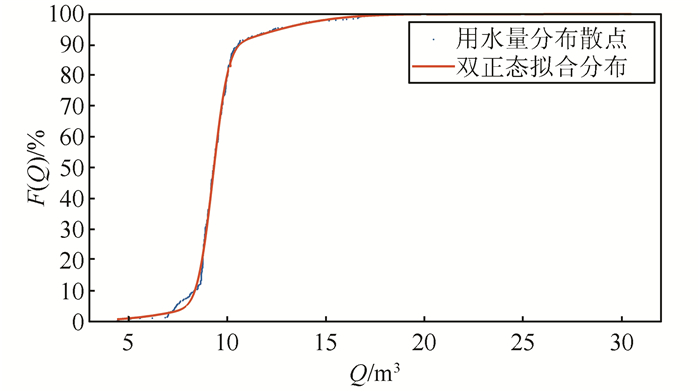
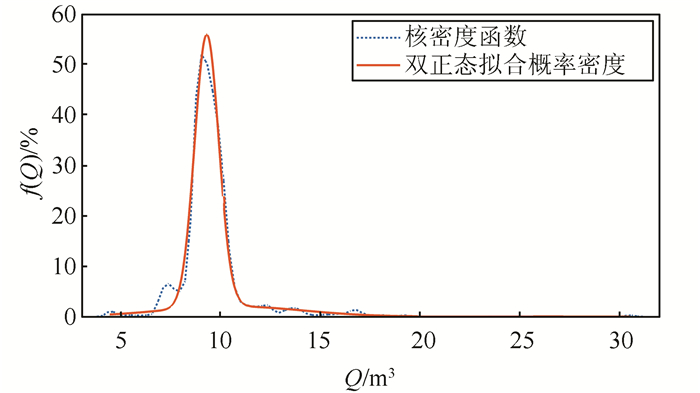
双正态叠加模型拟合实施阶梯水价前大连市的用水分布结果如表 1所示,其分布函数如图 3所示.双正态叠加模型的概率密度函数与核密度函数的对比如图 4所示.
| 参数 | a | b | c | d | k | R2 |
| 数值 | 9.294 | 0.606 3 | 10.6 | 3.512 | 0.820 7 | 0.996 6 |
|
| 图 3 双正态叠加分布拟合大连市居民用水量分布 Fig. 3 Double normal distribution fitting distribution of Dalian's residential water demand |
|
| 图 4 双正态叠加分布拟合的概率密度结果和核密度函数对比 Fig. 4 Contrast of probability density result fitted by double normal distribution and kernel density |
由图 1和图 3可见,双正态叠加模型拟合出大连市的居民用水分布比单一正态的拟合结果更接近真实分布.由图 2和图 4可见,双正态叠加模型拟合出的居民用水概率密度也比单一正态分布拟合结果更贴近样本数据的核密度函数,故双正态叠加模型比单一正态拟合有明显的优越性.通过大量的拟合试验,公式(1)对于居民户均用水量这类“类正态”的分布有着很好的拟合效果.由于此类分布随机因素较多,以居民户均用水量为例,它受户均人口分布、家庭收入分布等影响,且不同城市有着不同的分布规律,但公式(1)可以通过各系数的调节,使拟合结果尽可能地贴近原始数据,在本文居民户均用水量分布的拟合中,各系数的调节对7~9 m3和11~13 m3段的拟合效果的改善显而易见,故本文中后续阶梯水价方案实施前后大连市的用水分布均使用此模型,R2值均在0.996 6以上,明显高于单一正态分布的R2拟合值0.992 1.
2 居民用水的需求价格弹性 2.1 需求价格弹性理论由于阶梯水价是一种价格杠杆,目的是提高价格来抑制需求,故需求与价格的关系是计算阶梯水价节水效益的关键之一.本文阶梯水价的节水效益测算所依据的基本理论是需求价格弹性理论[14],如下式所示:
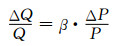 (2)
(2)
式中:Q和ΔQ分别为1户居民月均用水量和月均用水量的变化量;P和ΔP分别为水价和水价变化量;β为需求价格弹性系数.
故可根据居民生活用水的需求价格弹性和实施阶梯水价后水价的变化推算居民生活用水量的变化,从而计算出实施阶梯水价后各户居民用水量.
根据居民用水的需求价格弹性理论,结合用水量以及水价的变化数据,即可利用下式测算得出实施阶梯水价后各户居民的节水量ΔQi[15]:
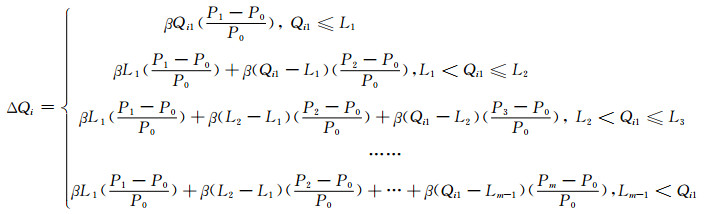 (3)
(3)
式中:Qi1表示某户居民i实施阶梯水价前的月用水量;ΔQi1表示该户居民实施阶梯水价后节约出来的水量;i=1, 2, 3, …, n,n为城市居民总户数;β为用水需求价格弹性;m为阶梯水价方案总阶梯数;Lm为第m-1阶梯和第m阶梯的分界水量;P0为阶梯水价实施前的统一价格,Pm为实施阶梯水价方案后第m级水价.计算出各户居民节水量ΔQi后,即可通过式(4)算出实施阶梯水价后各户居民的用水量Qi2:
 (4)
(4)
在居民用水需求价格弹性领域,已有的研究基本上均采用双对数模型进行居民用水需求价格弹性的拟合,本文也采用类似的方法[3-5].双对数模型认为居民用水需求和水价、收入等影响因素呈双对数线性关系,且存在随机干扰项.由于在我国部分缺水城市,当年水资源量可能会影响当年的供水情况,当年水资源量过少会导致供水遭受一定的影响,进而影响居民的用水量,故本文将当年水资源总量纳入双对数模型方程, 记为模型Ⅰ,其表达式为
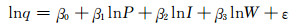 (5)
(5)
只考虑水价和收入的双对数模型记为模型Ⅱ,其表达式为
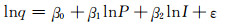 (6)
(6)
式(5)、(6)中:q为人均生活日用水量;I、P分别为以1999年物价水平为基准折算出的当年人均可支配收入和水价;W为当年水资源总量;ε为随机干扰项;β0为常数,β1为价格弹性,β2为收入弹性,β3为需求对水资源总量的弹性.通过统计以上数据多年的系列值加以回归拟合,即可得到需求价格弹性β1.
本文将2个模型的拟合结果进行对比,择优选用.
统计1999-2013年大连市的历史数据,包括消费品价格指数、城镇居民人均生活用水量、大连市水资源总量、大连市城镇居民人均可支配收入以及水价,如表 2所示.其中水资源总量应包括本地水资源总量和外调水量,由于大连市外调水工程——大伙房水库输水入连工程从2014年开始正式通水,故数据中不包含外调水量.1999-2013年,大连市居民水价经历了3次提价,提价年份分别为2001年、2004年和2012年.得到原始数据后再由消费品价格指数算得以1999年为基准的价格折算系数,从而得到以1999年为基准的水价和人均可支配收入(资料由各年份《大连市水资源公报》和《大连市统计年鉴》直接或间接计算而得).
| 年份 | 水价/(元·m-3) | 人均可支配收入/元 | 消费品价格指数 | 以1999年为基准的价格折算系数 | 城镇居民人均生活用水量q/(L·d-1) | 大连市水资源总量W/亿m3 | 以1999年为基准的水价P/(元·m-3) | 以1999年为基准的人均可支配收入I/元 |
| 1999 | 1.80 | 6 274 | 96.9 | 1.00 | 70.9 | 28.00 | 1.80 | 6 274 |
| 2000 | 1.80 | 6 860 | 99.4 | 1.01 | 87.9 | 25.40 | 1.81 | 6 902 |
| 2001 | 2.50 | 7 418 | 98.9 | 1.02 | 62.7 | 22.40 | 2.54 | 7 546 |
| 2002 | 2.50 | 8 199 | 97.7 | 1.04 | 63.5 | 6.35 | 2.60 | 8 537 |
| 2003 | 2.50 | 9 101 | 99.9 | 1.04 | 73.1 | 12.43 | 2.61 | 9 486 |
| 2004 | 2.90 | 10 377 | 102.4 | 1.02 | 92.8 | 27.72 | 2.95 | 10 562 |
| 2005 | 2.90 | 11 994 | 100.0 | 1.02 | 97.8 | 41.02 | 2.95 | 12 208 |
| 2006 | 2.90 | 13 350 | 101.0 | 1.01 | 76.8 | 22.10 | 2.92 | 13 453 |
| 2007 | 2.90 | 15 109 | 104.5 | 0.96 | 97.1 | 30.66 | 2.80 | 14 569 |
| 2008 | 2.90 | 17 500 | 105.7 | 0.91 | 99.9 | 19.91 | 2.65 | 15 966 |
| 2009 | 2.90 | 19 014 | 101.3 | 0.90 | 102.7 | 14.09 | 2.61 | 17 124 |
| 2010 | 2.90 | 21 293 | 103.0 | 0.87 | 105.5 | 39.26 | 2.54 | 18 618 |
| 2011 | 2.90 | 24 276 | 105.8 | 0.83 | 96.2 | 38.39 | 2.40 | 20 063 |
| 2012 | 3.10 | 27 480 | 103.4 | 0.80 | 96.4 | 71.67 | 2.48 | 21 964 |
| 2013 | 3.10 | 30 903 | 102.2 | 0.78 | 116.4 | 53.29 | 2.42 | 24 168 |
使用SPSS软件对历史数据按双对数模型Ⅰ、Ⅱ,即式(5)、(6)进行回归拟合,得出各回归系数β0、β1、β2、β3以及各类统计量,结果如表 3、4所示.
| 参数 | β0 | β1 | β2 | β3 | 相关系数 | F值 | F→p |
| 拟合值 | 1.415 (0.088) |
-0.130 (0.617) |
0.310 (0.011) |
0.076 (0.282) |
0.83 | 8.12 | 0.003 9 |
| 注:括号内为t统计量对应的概率. | |||||||
| 参数 | β0 | β1 | β2 | 相关系数 | F值 | F→p |
| 拟合值 | 1.106 (0.147) |
-0.237 (0.377) |
0.380 (0.001) |
0.808 | 11.275 | 0.002 |
| 注:括号内为t统计量对应的概率. | ||||||
观察模型拟合结果,模型Ⅰ、Ⅱ的相关系数分别为0.83和0.808,说明模型Ⅰ的因变量与自变量的相关性更强,模型Ⅰ的自变量能更好地解释因变量的变化.2个模型F统计量对应的p值分别为0.003 9和0.002,都通过了1%的显著性检验,说明模型整体的拟合效果都比较好.由于模型Ⅰ的相关系数较高,故本文选择模型Ⅰ的拟合结果.由模型Ⅰ的拟合结果可知,用水需求价格弹性为-0.13,即对单个用户而言,水价增长10%,用水需求将减少1.3%.
此外,由公式(2)可知,由于双对数模型中价格弹性β只受水量和水价的变化率的比值的影响,与水量的单位无关,故使用城镇居民生活人均日用水量拟合出的价格弹性β1可直接用于公式(3)中户月均用水量的节水计算.
3 阶梯水价节水比例和水费支出占收入比例测算 3.1 计算方法首先根据居民用水需求价格弹性以及公式(3)计算实施阶梯水价后所调查小区内用户的用水量变化情况,得到调查区域内的635户居民实施阶梯水价后的各户用水量Qi2,再按照第1章中介绍的双正态模型和方法重新拟合分布函数,得到实施阶梯水价后各方案的用水分布,然后根据实施阶梯水价前后的用水分布计算大连市实施阶梯水价前后户均用水量Q1和Q2,即为实施阶梯水价前后用水分布函数的期望E(Qi1)和E(Qi2).计算方法如下:
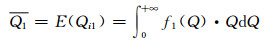 (7)
(7)
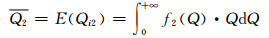 (8)
(8)
式中:f1(Q)和f2(Q)分别为实施阶梯水价前后大连市用水分布概率密度函数,分别由实施阶梯水价前后的大连市居民用水量分布函数F1(Q)和F2(Q)求导得到,其中F1(Q)和F2(Q)分别由Qi1和Qi2按照公式(1)拟合而得.
节水比例s可由下式计算得到:
 (9)
(9)
以大连市的3阶梯水价为例,计算实施阶梯水价后居民的户均水费支出C:
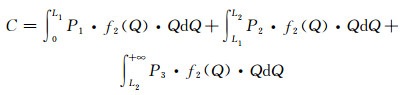 (10)
(10)
式中:f2(Q)为实施阶梯水价后的居民用水分布;P1、P2和P3分别为第1、第2和第3阶梯的水价;L1和L2分别为第1阶梯水量和第2阶梯水量.
则户均水费支出占户均可支配收入的比例r的计算式为
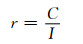 (11)
(11)
式中:C为户均水费支出;I为户均可支配收入.
3.2 大连市阶梯水价的节水效益与居民水费支出占收入比例国家发展改革委、住房城乡建设部印发的《关于加快建立完善城镇居民用水阶梯价格制度的指导意见》,部署全面实行城镇居民阶梯水价制度.2015年底前,设市城市原则上要全面实行居民阶梯水价制度,第1、2、3级阶梯水价按不低于1:1.5:3的比例安排,第1阶梯水量原则上覆盖80%的用户,第2阶梯水量原则上覆盖95%的用户.阶梯水价的初衷是“保低罚高”,然而水价改革并不仅限于对第2、第3阶梯用户进行加价惩罚,也要考虑第1阶梯水价是否合理,能否在一定程度上反映水资源市场的稀缺程度.本文以此原则为参考,设置7种第1阶梯水量覆盖比例(65%、70%、75%、80%、85%、90%和95%)以及6种提价比例(0%、10%、20%、30%、40%和50%),利用拟合出的大连市居民用水价格弹性和公式(3)计算大连市635户居民实施阶梯水价后的用水量,然后使用公式(1)的模型进行用水量分布函数的拟合,得到实施阶梯水价后的样本数据的用水量分布函数,作为大连市的居民用水量分布.最后应用3.1节中介绍的方法计算不同第1阶梯水量和第1阶梯水价下的s和r,如表 5、6所示.表中L1为第1阶梯水量,P1为第1阶梯水价.
| % | |||||||
| L1/m3 | 覆盖比例/% | P1/(元·m-3) | |||||
| 3.250 (0%) |
3.575 (10%) |
3.900 (20%) |
4.225 (30%) |
4.550 (40%) |
4.875 (50%) |
||
| 9.62 | 65 | 0.63 | 2.00 | 3.35 | 4.72 | 6.07 | 7.44 |
| 9.74 | 70 | 0.52 | 1.87 | 3.22 | 4.57 | 5.93 | 7.28 |
| 9.92 | 75 | 0.38 | 1.71 | 3.06 | 4.40 | 5.73 | 7.08 |
| 10.03 | 80 | 0.31 | 1.64 | 2.95 | 4.29 | 5.62 | 6.95 |
| 10.17 | 85 | 0.20 | 1.53 | 2.85 | 4.17 | 5.50 | 6.82 |
| 10.57 | 90 | 0.15 | 1.46 | 2.77 | 4.09 | 5.41 | 6.72 |
| 12.39 | 95 | 0.05 | 1.36 | 2.65 | 3.95 | 5.26 | 6.57 |
| 注:括号内表示提价比例. | |||||||
| % | |||||||
| L1/m3 | 覆盖比例/% | P1/(元·m-3) | |||||
| 3.250 (0%) |
3.575 (10%) |
3.900 (20%) |
4.225 (30%) |
4.550 (40%) |
4.875 (50%) |
||
| 9.62 | 65 | 0.51 | 0.53 | 0.56 | 0.58 | 0.60 | 0.62 |
| 9.74 | 70 | 0.49 | 0.52 | 0.54 | 0.56 | 0.59 | 0.61 |
| 9.92 | 75 | 0.47 | 0.50 | 0.52 | 0.55 | 0.57 | 0.59 |
| 10.03 | 80 | 0.45 | 0.48 | 0.51 | 0.54 | 0.56 | 0.59 |
| 10.17 | 85 | 0.44 | 0.47 | 0.49 | 0.52 | 0.55 | 0.57 |
| 10.57 | 90 | 0.42 | 0.45 | 0.48 | 0.51 | 0.53 | 0.56 |
| 12.39 | 95 | 0.39 | 0.43 | 0.46 | 0.49 | 0.51 | 0.54 |
| 注:括号内表示提价比例. | |||||||
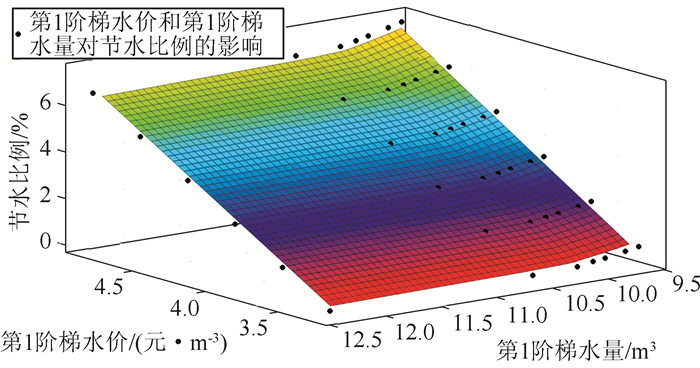
则节水比例s、水费支出占收入比例r和第1阶梯水价P1和第1阶梯水量L1的关系图如图 5、6所示.
|
| 图 5 第1阶梯水价、第1阶梯水量和节水比例关系图 Fig. 5 Relationship of first step price, first step volume and water-saving effect |

|
| 图 6 第1阶梯水价、第1阶梯水量和居民水费支出占收入比例关系图 Fig. 6 Relationship of first step price, first step volume and proportion of residential water fee expenditure to disposable income |
通过以上的研究与分析可以得到如下的结论:
1) 大连市的居民用水分布呈现轻微的正偏态分布,众数略小于期望值.大连市居民生活用水量的价格弹性为-0.13,即对单个居民用户而言,水价上升10%,其用水量下降1.3%.
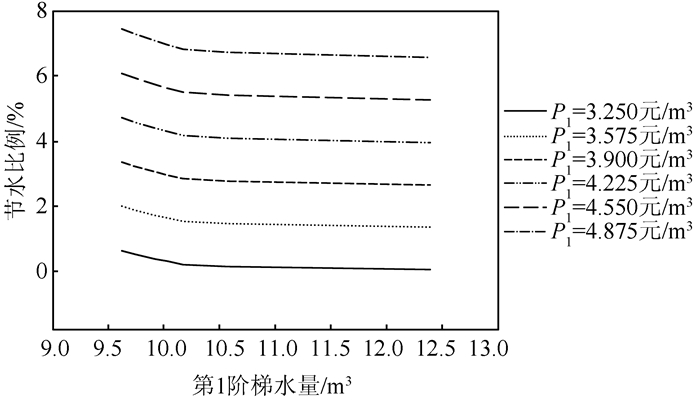
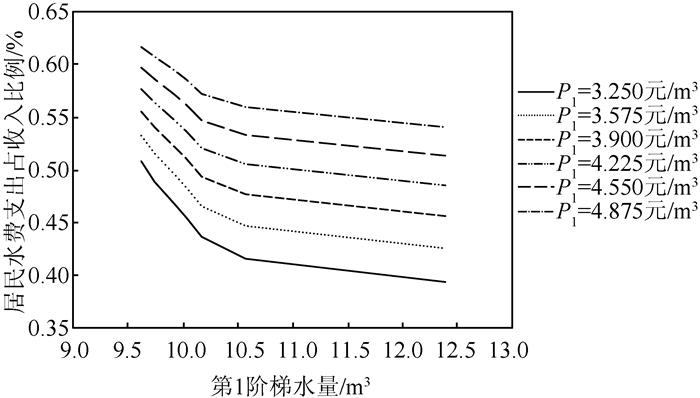
2) 第1阶梯水价P1一定的情况下,随着第1阶梯水量L1的降低,节水比例s和居民水费支出占收入比例r都会变高,且变高的速率会逐渐增大.当L1降至10.2 m3时,s和r都开始显著增大,如图 7、8所示.
|
| 图 7 节水比例随第1阶梯水量的变化 Fig. 7 Relationships between water-saving effect and first step water volume |
|
| 图 8 居民水费支出占收入比例随第1阶梯水量的变化 Fig. 8 The relation between theproportion of residential water fee expenditure to disposable income and the first step volume |
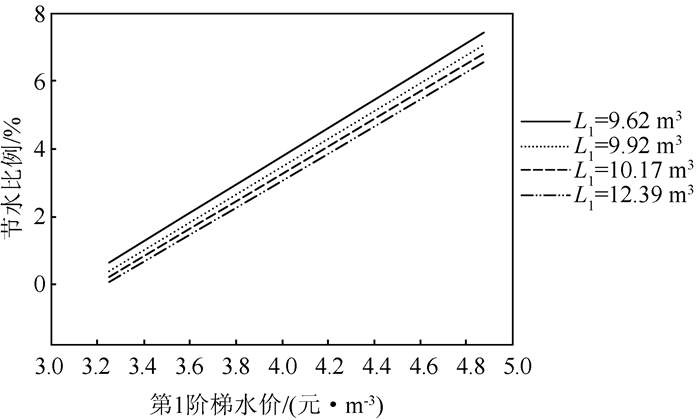
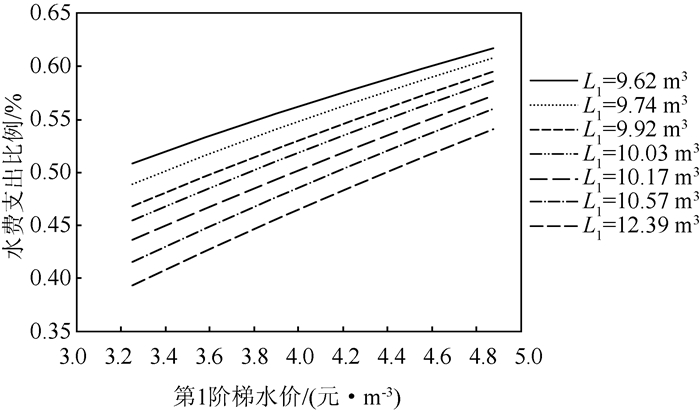
L1一定的情况下,随着P1的上升,s也与P1呈近似线性比例上升,如图 9所示.r同样也随着第1阶梯水价的上升而增高,但并不是严格的线性变化,由于水价上升后,部分居民的用水量会减少,故r随P1上升而增高的速率会有轻微变小的趋势,如图 10所示.
|
| 图 9 节水比例随第1阶梯水价的变化 Fig. 9 The relation between water-saving effect and the first step price |
|
| 图 10 居民水费支出占收入比例随第1阶梯水价的变化 Fig. 10 Relationships between proportion of residential water fee expenditure to disposable income and first step water price |
3) 由图 9可知,提高第1阶梯水价P1和降低第1阶梯水量L1都可以增大节水比例,提高P1对节水比例的影响要明显大于降低L1.由于不同L1下,s随P1的变化趋势相似,以L1=10.17 m3为例,当L1=10.17 m3时,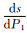
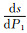
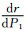

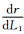
本文测算的阶梯水价方案节水比例为0.05%~ 7.44%,居民水费支出占收入比例为0.39%~0.62%.居民水费支出占收入比例远低于国家推荐的标准2.5%~3%[15],故大连市水价还有很大的提价空间.
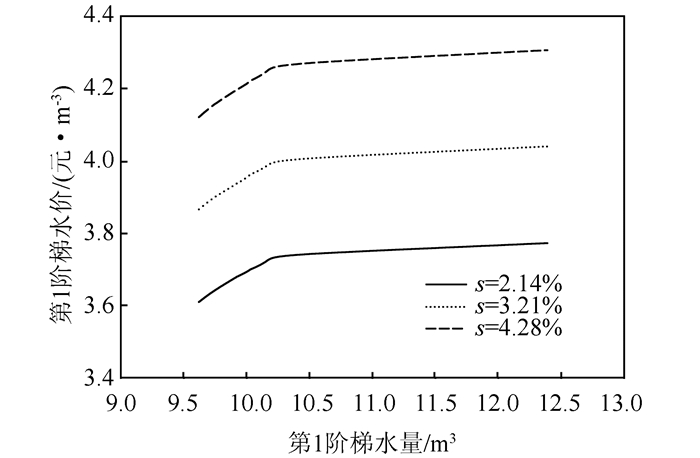
4) 根据2015年《大连市水资源公报》,大连市2015年城镇生活用水4.67亿m3,假设预期节水量分别为1 000万m3、1 500万m3和2 000万m3,则节水比例分别为2.14%、3.21%和4.28%,可由图 5截取节水比例s分别等于2.14%、3.21%和4.28%的水平面或根据表 5插值,即可找出可行方案点集,如图 11所示.
|
| 图 11 不同节水比例下的可行方案集 Fig. 11 Feasible solution set under different water-saving effects |
根据图 7可知,当L1降至10.2 m3(覆盖比例约85%)以下时,s的变化率显著增大.由图 11可知,为达到同样的节水效益,P1也会明显降低,则第1阶梯用户的利益受到了一定程度的保护,阶梯水价方案才能体现出其初衷和本质优势,即“保低罚高”,尽量不让第1阶梯的用户为以节水为目的的提价而买单.故阶梯水价方案第1阶梯水量宜位于10.2 m3以下,但同时由于第1阶梯水量的目的是保证居民基本生活用水需求,故L1也不应小于城市居民基本生活用水需求量.
大连市现阶段居民水费支出占可支配收入比例为0.37%,远低于国际和国家标准,故大连市水价尚有充足的提价空间.从提高居民水费支出占可支配收入比例的角度,假设预期水费支出占收入比例为0.45%、0.50%和0.55%.可由图 6截取居民水费支出占收入比例r分别等于0.45%、0.50%和0.55%或根据表 6插值,即可找出可行方案集,如图 12所示.可见不同的水费支出水平下,可行方案的第1阶梯水价均会随第1阶梯水量的增大而增大.

|
| 图 12 不同居民水费支出占收入比例下的可行方案集 Fig. 12 Feasible solution set under different proportions of residential water fee expenditure to disposable income |
如此分析即可得到各预期节水比例和居民水费支出水平下的可行方案集,决策者可根据对阶梯水价方案预期的节水效益和居民水费支出水平,结合图 5、图 6、图 11和图 12找出合适的阶梯水价方案.也可以在考虑居民对第1阶梯水价和第1阶梯水量的接受程度的情况下,进行多目标决策分析,寻找最佳方案.
| [1] |
张嵘, 吴静芳. 基于扩展线性支出理论的阶梯水价模型[J]. 科学技术与工程, 2009, 9(3): 641-645. Zhang Rong, Wu Jingfang. Ladder pricing model based on ELES theory[J]. Science Technology and Engineering, 2009, 9(3): 641-645. DOI:10.3969/j.issn.1671-1815.2009.03.025 |
| [2] |
贾国宁, 黄平. 居民用水阶梯式水价及其节水效果测算模型研究[J]. 自然资源学报, 2013, 28(10): 1789-1796. Jia Guoning, Huang Ping. Staged water price and the water-saving effect calculation mode for domestic water[J]. Journal of Natural Resource, 2013, 28(10): 1789-1796. |
| [3] |
魏丽丽, 付强, 陈丽燕. 哈尔滨市居民生活用水需求弹性分析[J]. 东北农业大学学报, 2008, 39(7): 34-37. Wei Lili, Fu Qiang, Chen Liyan. Elastic analysis on the water demand of urban residential of Harbin[J]. Journal of Northeast Agricultural University, 2008, 39(7): 34-37. DOI:10.3969/j.issn.1005-9369.2008.07.009 |
| [4] |
尹建丽, 袁汝华. 南京市居民生活用水需求弹性分析[J]. 南水北调与水利科技, 2005, 3(1): 46-48. Yin Jianli, Yuan Ruhua. Analysis of the Nanjing domestic water demand[J]. South-to-North Water Transfers and Water Science & Technology, 2005, 3(1): 46-48. DOI:10.3969/j.issn.1672-1683.2005.01.016 |
| [5] |
沈大军, 杨小柳, 王浩, 等. 我国城镇居民家庭生活需水函数的推求及分析[J]. 水利学报, 1999, 30(12): 6-10. Shen Dajun, Yang Xiaoliu, Wang Hao, et al. Analysis of urban residential water demand functions in China[J]. Journal of Hydraulic Engineering, 1999, 30(12): 6-10. DOI:10.3321/j.issn:0559-9350.1999.12.002 |
| [6] |
张宁, 章胜. 基于双对数模型的城市居民用水需求弹性分析[J]. 工业技术经济, 2010, 29(3): 50-53. Zhang Ning, Zhang Sheng. Elastic analysis on the water demand of urban residents based on log-log model[J]. Journal of Industrial Technological Economics, 2010, 29(3): 50-53. DOI:10.3969/j.issn.1004-910X.2010.03.014 |
| [7] |
邢秀凤, 吴艳丽. 城市居民生活用水需求弹性实证分析[J]. 技术经济与管理研究, 2007(2): 35-36. Xing Xiufeng, Wu Yanli. Empirical analysis on the water demand elasticity of urban residents[J]. Technoeconomics & Management Research, 2007(2): 35-36. DOI:10.3969/j.issn.1004-292X.2007.02.013 |
| [8] |
董凤丽, 韩洪云. 沈阳市城镇居民生活用水需求影响因素分析[J]. 水利经济, 2006, 24(3): 23-27. Dong Fengli, Han Hongyun. Analysis of influencing factors for demand of domestic water for dwellers in Shenyang City[J]. Journal of Economics of Water Resources, 2006, 24(3): 23-27. DOI:10.3969/j.issn.1003-9511.2006.03.008 |
| [9] |
李翠梅, 陶涛, 刘遂庆. 苏州市居民生活用水量价格弹性研究[J]. 给水排水, 2010, 36(5): 171-174. DOI:10.3969/j.issn.1002-8471.2010.05.042 |
| [10] |
潘莉, 朱世晨. 某地区阶梯水价的定价合理性研究[J]. 人民黄河, 2015, 37(10): 62-65. Pan Li, Zhu Shichen. Rationality study on differential water pricing of region[J]. Yellow River, 2015, 37(10): 62-65. DOI:10.3969/j.issn.1000-1379.2015.10.016 |
| [11] |
柳长顺, 陈献, 刘昌明, 等. 华北地区城镇居民水费支出占收入与消费的比例研究[J]. 水利经济, 2005, 23(3): 27-32. Liu Changshun, Chen Xian, Liu Changming, et al. Study of the proportion of residential water fee expenditure to disposable income of urban residents of North China[J]. Journal of Economics of Water Resources, 2005, 23(3): 27-32. |
| [12] |
Rosenblatt M. Remarks on some nonparametric estimates of a density function[J]. Annals of Mathematical Statistics, 1956, 27(6): 832-837. |
| [13] |
Parzen E. On estimation of a probability density function and mode[J]. Annals of Mathematical Statistics, 1962, 33(8): 1065-1076. |
| [14] |
Robert S Pindyck, Daniel L Rubinfeld. Microeconomics[M]. 北京: 中国人民大学出版社, 2013: 31-36.
|
| [15] |
唐要家, 李增喜. 居民递增型阶梯水价政策有效性研究[J]. 产经评论, 2015, 6(1): 103-113. Tang Yaojia, Li Zengxi. A study on the effectiveness of the Increasing block water tariffs[J]. Industrial Economics Review, 2015, 6(1): 103-113. |
 2019, Vol. 52
2019, Vol. 52




