文章信息
- 麻妍妍, 夏军强, 张晓雷
- MA Yanyan, XIA Junqiang, ZHANG Xiaolei
- 现有动床阻力计算公式验证与比较
- Verification and comparison of flow resistance formulae over movable beds
- 武汉大学学报(工学版), 2017, 50(4): 481-486
- Engineering Journal of Wuhan University, 2017, 50(4): 481-486
- http://dx.doi.org/10.14188/j.1671-8844.2017-04-001
-
文章历史
- 收稿日期: 2016-06-20
动床阻力是河流动力学研究的核心内容之一.动床阻力反映了河床对水流作用力的大小,决定了泥沙运动强度与水位抬升程度;另一方面,冲积河流的挟沙能力及河床冲淤变形均与动床阻力有极为密切的关系,因此有必要进一步开展冲积河流动床阻力的研究,以便为水利工程的修建提供科学参考[1].然而由于水沙因子随时间、空间变化的多样性及边界可动性,动床阻力问题极为复杂.特别是在黄河下游河段,水沙变化与河床调整更为复杂,动床阻力问题尤为突出.动床阻力常通过阻力系数来反映,常用的阻力系数有曼宁系数(n)、谢才系数(C)和达西-魏斯巴赫阻力系数(f).现有对阻力系数的研究方法主要有两类:一是单独研究阻力单元系数;二是直接探索综合阻力系数的变化规律.
动床阻力一般分为沙粒阻力和沙波阻力两个阻力单元.已有学者对阻力单元进行了研究:黄才安等[2]根据相对等效粗糙度(λ)曲线与希尔兹(θc)曲线的相似性,从泥沙起动角度出发提出了沙粒阻力的计算方法.Van Rijn[3]以谢才系数为研究对象,分析了密西西比河等河流及水槽床面形态对谢才系数变化的影响,并建立两者之间的关系式.Yang与Tan[4]通过水槽试验得到了边壁、河床形态及相对粗糙度(d/h)与床面阻力的经验关系式,该式具有较高的计算精度.由于阻力单元起源并不同,因此对总阻力进行划分、分解,有助于更准确严格地理解动床阻力的产生及作用机理.但其计算过程繁琐、工作量大,在实际工程中应用较少.
综合阻力系数的研究方法对沙粒阻力和沙波阻力不加以区分,以实测资料为依据直接建立综合阻力系数与水沙因子的关系式,前人已在这方面开展了大量的研究工作.Habibi等[5]研究了大比降粗糙河床的床面阻力特性,得到相对粗糙度、比降(J)和弗劳德数(Fr)为影响曼宁系数变化的主要因素的结论,并根据试验资料给出了综合考虑这些因素的曼宁系数计算方法.张红武等[6]在动床模型试验的基础上,将沙波波速、尺度综合考虑在糙率计算式中.Yalin[7]在研究河床形态对阻力的影响时,基于Engelund[8]的研究通过量纲分析建立剪切力(θ)与有效剪切力(θ′)和相对粗糙度之间的关系.王士强[9]根据冲积河床阻力试验进一步指出剪切力还应与特征粒径(D*)有关.秦荣昱等[10]在分析黄河下游河道阻力变化规律时,将卡门系数作为阻力变化的起因,提出了计算黄河下游河道超低阻力的方法.总之,目前对动床阻力的大多数研究都是将水流条件、床面形态及床沙组成作为影响因素.虽然前人对动床阻力的研究成果较多,但各个阻力公式的精度及适用范围不同,实际应用方面还存在一定问题.
本文以张红武、秦荣昱、Van Rijn提出的动床阻力公式为研究对象,通过对公式计算精度进行对比分析,以确定各自的适用范围.此外,由于黄河下游主流摆动不定、河势变化剧烈,动床阻力的复杂程度高于一般河流,因此为了更好地进行工程设计,有必要进一步研究其阻力特性.本文以黄河下游1957-1998年实测资料为依据,分析了糙率与弗劳德数的变化关系,并建立两者之间的经验关系.
1 动床阻力公式介绍在阻力计算中,对阻力进行分割的方法有助于更准确严格地理解动床阻力的产生及作用机理,但计算过程过于繁琐,故在实际应用中多采用计算简便的综合阻力系数反映动床阻力.部分综合阻力系数计算公式需要试算,如:Wu[11]、Yang[4]提出的公式等;部分公式虽不需试算,但适用条件与本文所用资料相去甚远.为此本文选择适用范围较广且无需试算的3个动床阻力公式:张红武、秦荣昱和Van Rijn提出的公式进行验证与比较,验证资料包括64组水槽数据和1 121组河道数据.
张红武和赵连军[6]在黄河下游高含沙水流阻力特性的研究中以糙率为研究对象,引入了水流摩阻厚度的概念,并给出了其与弗劳德数和中值粒径的关系式.提出的糙率计算公式形式虽然复杂,但综合考虑了涡团参数、摩阻厚度及弗劳德数等水沙因素,糙率的表达形式如下:
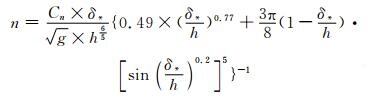 (1)
(1)
式中:Cn为涡团参数;δ*为摩阻厚度,mm;h为水力半径(宽浅河流R≈h),m.公式适用于黄河铁谢至孙口河段的动床糙率计算.
秦荣昱[10]将糙率系数的变化归结为卡门系数的改变,并建立卡门系数与水沙因子的关系.公式中的粗糙度只考虑沙粒阻力的作用,且糙率随流速的增加而减小,可用于计算黄河下游河道超低阻力,具体表达式为
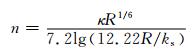 (2)
(2)
式中:ks为粗糙度,这里取ks为d65床沙,mm;κ为卡门系数,κ=3.4(Fr/ω5 0)-0.5,Fr为水流弗劳德数[12];ω50为粒径为d50床沙的沉速,m/s.公式适用于含沙量S<200 kg/m3的动床糙率计算.
Van Rijn[3]在床面粗糙度的研究中,综合考虑了沙粒阻力和沙波阻力对粗糙度的作用,建立谢才系数与水流条件、粗糙度的关系,并以输移系数(T)与特征粒径的变化规律为依据划分能态区域,结果表明该式适于计算低能态区、过渡区及高能态区(逆行沙波除外)的动床阻力,谢才系数的计算方法如下:
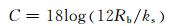 (3)
(3)
为方便糙率求解及各公式对比,将曼宁公式n=R1/6/C变换得到
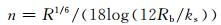 (4)
(4)
式中:R为水力半径,m;Rb为与河床阻力对应的水力半径,m,由Vanoni和Brooks方法[13]计算得到;这里取粗糙度ks=3d90+1.1Δ(1-e-25Δ/(λh)),mm;Δ、λ分别为沙波波高、波长,mm; d90为床沙粒径.公式适用于床沙粒径d介于0.16~3.6 mm范围内的河床糙率计算.
2 公式验证与比较 2.1 验证数据来源由于王士强[9]的冲积河渠床面阻力试验成果对沙波发展过程的描述足够准确,且黄河下游水文站多、资料较齐全,因此以王士强水槽试验成果及黄河下游花园口至利津河段9个水文站的实测资料为依据来验证阻力公式是合适的,如下所示:
1) 水槽试验资料.王士强[9]在可调坡循环水槽中进行冲积河渠床面阻力试验,通过研究不同水深、比降及粒径在高、低能区和过渡区对床面阻力影响的规律,得到64组包含水流、泥沙的资料.此外,根据床沙粒径级配曲线可得:d50=0.078 mm,d65=0.086 mm,d90=0.1 mm.
2) 河道资料.本文选用的是来自黄河下游9个水文站的1 000多组实测数据,受不同水文站及野外测量条件的限制,测量数据不能全部用于动床阻力计算.为加强验证结果的准确性,需对实测数据按照以下原则进行筛选,以剔除有问题的资料:
① 洪水漫滩下的水深沿断面分布极不均匀,直接计算导致糙率结果偏小,应舍去漫滩数据.
② 资料中应包括完整的流量、河宽、水深、比降、泥沙粒径及比重等内容.
③ 结合黄河下游河段实际情况,比降应在(1.5~4.0)×10-4之间.
根据上述原则对收集到的实测资料进行适当处理和筛选,筛选处理后本文实际使用的数据见表 1.从表 1的汇总可以看出,用于验证的数据范围较广,故利用这些数据对动床阻力公式进行验证可使其范围更全面,结果更精确.
| 数据来源 | 数据组数 | Q/(m3·s-1) | h/m | Fr |
| 水槽 | 64 | 0.024 6~0.409 9 | 0.062~0.365 | 0.157~0.853 |
| 河道 | 1 121 | 8~13 600 | 0.055 3~11.29 | 0.073~1.050 |
| 总计 | 1 185 | 0.024 6~13 600 | 0.055 3~11.29 | 0.073~1.050 |
综合阻力系数研究中曼宁糙率的研究最为广泛.曼宁糙率系数n=R2/3J1/2/U(R为水力半径,J为水面比降,U为断面平均流速),是反映河床阻力大小的重要水力参数.采用上述资料对3种动床阻力公式进行验证.
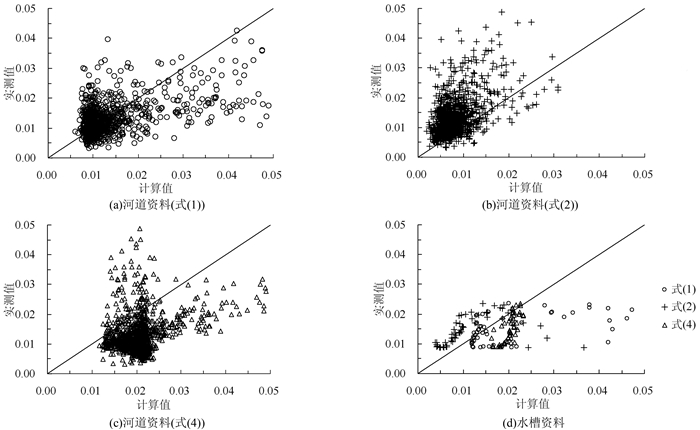
图 1(a)~(c)给出了利用河道资料计算得到的曼宁糙率与实测值的对比结果.由图 1可知,张红武公式和Van Rijn公式计算得到的糙率比实测值偏大,秦荣昱公式计算得到的糙率比实测值偏小.秦荣昱公式计算的糙率最小值可达0.003,属于超低阻力,且在糙率小于0.01范围内计算值与实测值比较接近,说明秦荣昱公式预报黄河下游超低河道阻力有一定的准确性.从图 1(a)还可以看出,糙率在小于0.015的范围内,数据密集地分布在45°线两侧,说明张红武公式对较低河道阻力的预报较为精确.根据图 1(c),Van Rijn公式计算得到的点在45°线两侧比较分散,说明其计算动床阻力误差较大.由实测资料得知黄河下游床沙中值粒径d50为0.028~0.187 mm,而Van Rijn公式适用于床沙粒径d为0.16~3.6 mm范围内的河床阻力计算,这是造成误差较大的主要原因.
|
| 图 1 糙率计算值与实测值对比 Figure 1 Comparison between the calculated and observed roughness |
图 1(d)给出了利用水槽资料计算得到的曼宁糙率与实测值的对比结果.根据图 1(d),计算值与实测值之间的对比情况与利用河道资料计算的结果一致:张红武公式和Van Rijn公式计算得到的糙率比实测值偏大,秦荣昱公式计算得到的糙率比实测值偏小.通过与资料对比,阻力较大时所对应的流量、断面尺寸及流速均较小,其主要原因在于流速较小时,泥沙处于刚起动或静止状态,多为推移质,而推移质的存在增加能量损失,故阻力也相应较大.
2.3 不同公式比较为避免因评价标准不同而导致评估结果产生差异,本文选择统一的评价标准对公式精度进行比较.对引起误差的影响因素进行了分析与总结,这有助于在以后的研究中尽量避免或减小这些影响,从而减小计算误差.
1) 评价标准与精度结果.本文利用3个统计参数(偏差比R、几何标准差AGD、均方根RMS)对计算结果与实测值的符合程度进行衡量,并给出偏差比在±10%、±20%、±30%内的比例.
表 2给出了上述各公式在计算河道阻力时的精度.依据表 2可知,对于张红武公式,偏差比在±30%内的百分比为54.8%,几何标准差为1.006 7,通过对比可知张红武公式计算黄河下游河道阻力精度最高.秦荣昱公式、Van Rijn公式偏差比在±30%内的百分比分别为35.2%、28.6%,几何标准差分别为1.006 9、1.012 3,故3个阻力公式的精度由高到低依次为:张红武公式、秦荣昱公式、Van Rijn公式.
| 公式 | 不同偏差比范围内的数据所占百分数/% | AGD | RMS | ||
| 0.9~1.1 | 0.8~1.2 | 0.7~1.3 | |||
| Van Rijn | 8.99 | 19.96 | 28.60 | 1.012 3 | 0.008 2 |
| 张红武 | 21.42 | 38.02 | 54.81 | 1.006 7 | 0.007 9 |
| 秦荣昱 | 9.35 | 20.87 | 35.21 | 1.006 9 | 0.007 8 |
各公式利用水槽资料计算阻力时的精度如表 3所示.根据表 3的结果,Van Rijn公式与张红武公式的偏差比在±10%、±20%、±30%内的百分比相近,但Van Rijn公式均方根为0.006 2,远小于张红武公式的0.026 3,故Van Rijn公式的计算精度较高.3个阻力公式的计算精度由高到低依次为:Van Rijn公式、张红武公式、秦荣昱公式.
| 公式 | 不同偏差比范围内的数据所占百分数/% | AGD | RMS | ||
| 0.9~1.1 | 0.8~1.2 | 0.7~1.3 | |||
| Van Rijn | 21.82 | 36.36 | 43.64 | 1.083 | 0.006 2 |
| 张红武 | 18.97 | 36.21 | 46.55 | 1.086 | 0.026 3 |
| 秦荣昱 | 5.26 | 14.04 | 24.56 | 1.076 | 0.008 8 |
2) 误差分析.基于以上计算可知,动床阻力公式预报值的误差普遍较大.影响阻力计算精度的因素有很多,本文主要从以下几个方面进行讨论:
① 过水断面形状矩形化.黄河下游河道横断面一般为复式断面,河槽极为宽浅,即使不考虑边滩影响,主槽过水断面仍为不规则的几何形状,水深在断面上分布不均匀.本文采用平均水深计算流速,即把断面形状概化为矩形,所产生的流速误差必定影响阻力计算精度.
② 床面形态判别的复杂性.目前对河床形态的判别还没有统一标准,不同学者的判别方法均为基于各自研究的经验公式.如王士强根据阻力系数随有效剪切力变化规律的不同划分能态区域;法国夏都水利实验室根据希尔兹数与沙粒雷诺数(Re*)的关系图判别床面形态.在具体计算中,选择不同的床面形态判别准则会产生不同的计算误差.
③ 水流泥沙因子随时间、空间变化的多样性也会影响计算精度.由于黄河水沙异源,加之两岸人类活动干扰程度不同,因此流量与含沙量在时间和空间的变化均具多样性.
④ 水文站资料测量的误差.对于天然河流,受自然及设备条件的限制,测量设备误差和风产生的水面波动使得所测比降不够准确.此外,床沙粒径的测量误差也较大.
⑤ 公式率定时所用资料会影响公式的计算精度.张红武公式、秦荣昱公式的提出是基于黄河下游阻力特性的分析研究,故比较适用于计算黄河下游河道阻力;而Van Rijn公式在率定时以水槽资料为主,故对计算水槽动床阻力更加适用.
准确计算动床阻力对计算流量、水深等水力参数及认识河床冲淤特性具有重要意义.以往研究成果中,部分学者在特定水流条件下,提出相应的阻力计算公式一般不具普遍性,因此需要继续研究水沙条件与河床形态影响阻力变化的机理,提出动床阻力计算方法.
3 糙率系数的影响因素分析动床阻力与水流强度、含沙量、床沙组成和床面形态等密切相关.邓安军等[14]在黄河下游床面糙率的影响研究中指出糙率n随含沙量S的变化规律:含沙量S在10~100 kg/m3范围内,n的变化幅度不大;S<10 kg/m3时,n随S增大而减小;S>100 kg/m3时,n随S增大而增大.
床面形态随水流条件的逐渐增强依次表现为静平整、沙纹、沙垄、动平床、逆行沙垄和驻波等几种状态[15].对应于床面形态发展过程,床面阻力表现出不同的变化规律:随着床面平整至出现沙波,床面阻力逐渐增大;当沙波刚进入动平整状态时阻力达到最大,而后随着动平床的发展阻力逐渐减小;从动平整状态进入逆行沙波状态时,阻力呈增加趋势.要准确地表述阻力关系,合理地判别床面形态是必不可少的,但目前关于这方面的研究成果较少且不成熟.
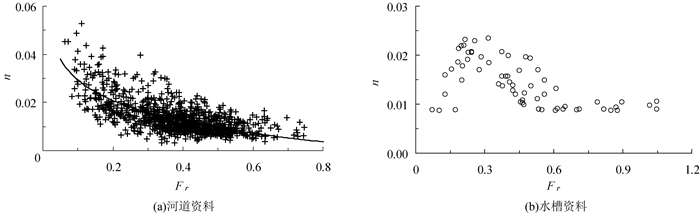
本文主要分析水流强度对曼宁糙率系数的影响,图 2(a)、(b)分别给出了黄河下游和水槽中床面糙率随弗劳德数变化规律.由于黄河断面宽浅且流量相对较小,使得其流速较小,水流处于缓流状态,故水流弗劳德数多小于1.0.从图 2(a)可以看出,糙率与弗劳德数呈负相关,即糙率随弗劳德数的增大而减小,并最终趋于0.005达到最小值.根据图 2(b),存在一临界弗劳德数,当弗劳德数小于该临界值时,糙率与弗劳德数呈正相关,即糙率随弗劳德数增大而增加;当弗劳德数大于该临界值时,糙率与弗劳德数呈负相关,此变化规律对应沙波的消长过程.而本文中河道糙率没有表现出这种规律,可能原因是临界弗劳德数小于最小弗劳德数0.08.
|
| 图 2 糙率与弗劳德数关系 Figure 2 Relation between roughness and Froude number |
根据图 2(a)中点拟合得到糙率与弗劳德数的经验关系式(相关系数R2=0.501):
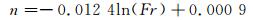 (5)
(5)
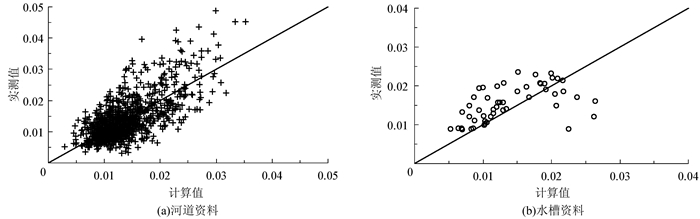
图 3给出了利用式(5)计算的糙率与实测值的对比结果,从图中可看出,糙率较小时点密集地分布在45°线周围,说明公式计算精度较高;n>0.02时,糙率与弗劳德数的关系比较散乱,说明计算值与实测值偏差较大.
|
| 图 3 计算糙率与实测糙率对比 Figure 3 Comparison between the calculated and observed roughness coefficient |
表 4给出了式(5)计算的精度结果.根据表 4可知,河道糙率的计算误差在±10%、±20%、±30%内的百分比分别为23.26%、44.54%、61.68%,水槽中河床糙率相应的计算误差分别为35.29%、56.86%、68.63%,与本文验证的3个阻力公式比较可知,式(5)的计算精度相对较高.
| 数据来源 | 不同偏差比范围内的数据所占百分数/% | AGD | RMS | ||
| 0.9~1.1 | 0.8~1.2 | 0.7~1.3 | |||
| 河道 | 23.26 | 44.54 | 61.68 | 1.007 | 0.004 9 |
| 水槽 | 35.29 | 56.86 | 68.63 | 1.086 | 0.001 1 |
动床阻力公式较多,不同公式的适用条件及计算精度不同.本文选取国内外3个动床阻力计算公式,利用64组水槽资料及1 121组黄河实测资料对其进行了验证与比较,并分析了水流弗劳德数对糙率的影响.主要得到如下结论:
1) Van Rijn公式在计算水槽的动床阻力时精度较高,而对天然河道阻力,张红武公式和秦荣昱公式计算精度较高,其中张红武公式精度最高.
2) 以黄河下游实测资料为依据,建立了糙率与弗劳德数的对数型经验关系式,该式能较好地反映黄河下游及水槽中床面糙率受水流条件的影响,对河道及水槽的动床阻力计算有较高的精度.
| [1] |
钱宁, 万兆惠.
泥沙运动力学[M]. 北京: 科学出版社, 1983: 192-198.
Qian Ning, Wan Zhaohui. Mechanics of Sediment Transport[M]. Beijing: Science Press, 1983: 192-198. |
| [2] |
黄才安. 冲积河流水流泥沙运动基本规律的研究[D]. 南京: 河海大学, 2004.
Huang Caian. Study on the basic laws of flow and sediment transport in alluvial channels[D]. Nanjing: Hohai University, 2004. http://cdmd.cnki.com.cn/Article/CDMD-10294-2004050309.htm |
| [3] | Van Rijn L C. Sediment transport, Part Ⅲ: Bed forms and alluvial roughness[J]. Journal of Hydraulic Engineering, 1984, 110(12): 1733–1754. DOI:10.1061/(ASCE)0733-9429(1984)110:12(1733) |
| [4] | Yang S Q, Tan S K. Flow resistance over mobile bed in an open-channel flow[J]. Journal of Hydraulic Engineering, 2008, 134: 937–947. DOI:10.1061/(ASCE)0733-9429(2008)134:7(937) |
| [5] | Habibi M, Namaee M R, Saneie M. An experimental investigation to calculate flow resistance in a steep river[J]. Journal of Civil Engineering, 2014, 18(4): 1176–1184. |
| [6] |
赵连军, 张红武. 黄河下游河道水流摩阻特性的研究[J].
人民黄河, 1997(9): 17–20.
Zhao Lianjun, Zhang Hongwu. Study of flow frictional characteristics in the Lower Yellow River Channel[J]. Yellow River, 1997(9): 17–20. |
| [7] | Yalin M S. Mechanics of Sediment Transport[M]. Oxford: Pergamon Press, 1977. |
| [8] | Engelund F. Hydraulic resistance of alluvial streams[J]. Journal of Hydraulic Division, 1966, 98: 315–326. |
| [9] |
王士强. 冲积河渠床面阻力试验研究[J].
水利学报, 1990(12): 18–29.
Wang Shiqiang. Experimental study on hydraulic resistance of alluvial streams[J]. Journal of Hydraulic Engineering, 1990(12): 18–29. DOI:10.3321/j.issn:0559-9350.1990.12.003 |
| [10] |
秦荣昱, 刘淑杰, 王崇浩. 黄河下游河道阻力与输沙特性的研究[J].
泥沙研究, 1995(4): 10–18.
Qin Rongyu, Liu Shujie, Wang Chonghao. Characteristics of channel resistance and sediment transport in the Lower Yellow River[J]. Journal of Sediment Research, 1995(4): 10–18. |
| [11] | Wu W M, Wang S S Y. Movable bed roughness in alluvial rivers[J]. Journal of Hydraulic Engineering, 1999(125): 1309–1312. |
| [12] |
秦荣昱. 动床水流卡门常数变化规律的研究[J].
泥沙研究, 1991(3): 38–52.
Qin Rongyu. Karmen coefficient of flow with movable bed[J]. Journal of Sediment Research, 1991(3): 38–52. |
| [13] | Vanoni V A, Brooks N H. Laboratory Studies of the Roughness and Suspended Load of Alluvial Streams[M]. California: Pasadena Press, 1957: 100-106. |
| [14] |
邓安军, 郭庆超, 陈建国. 挟沙水流综合糙率系数的研究[J].
泥沙研究, 2007(5): 24–29.
Deng Anjun, Guo Qingchao, Chen Jianguo. Study on the roughness in sediment-laden flows[J]. Journal of Sediment Research, 2007(5): 24–29. |
| [15] |
王兴奎, 邵学军, 李丹勋.
河流动力学基础[M]. 北京: 中国水利水电出版社, 2002: 132-143.
Wang Xingkui, Shao Xuejun, Li Danxun. Fundamental River Mechanics[M]. Beijing: China WaterPower Press, 2002: 132-143. |
 2017, Vol. 50
2017, Vol. 50




