文章信息
- 郑征, 王莹秋
- ZHENG Zheng, WANG Yingqiu
- 级联H桥整流器控制策略
- Control strategy of cascaded H-bridge rectifier
- 武汉大学学报(工学版), 2018, 51(2): 159-164, 171
- Engineering Journal of Wuhan University, 2018, 51(2): 159-164, 171
- http://dx.doi.org/10.14188/j.1671-8844.2018-02-010
-
文章历史
- 收稿日期: 2016-03-19
随着电力电子技术和现代控制理论的发展,新型的无工频变压器级联式功率变换器因其利用DC-DC变换器中的高频变压器实现网侧与负载侧间的电气隔离,省去了工频变压器,同时具有高功率因数、谐波污染小等优势,因此在高压电气传动、高压直流输电等方面得到广泛的应用.但由于其整流级直接与高压电网相连,若各桥直流侧电压不均衡易造成器件损坏,同时也会对后级逆变电路产生影响,产生大量谐波,因此亟待解决的问题就是各桥直流侧母线电压的平衡[1-2].
目前对级联整流器电压平衡控制多采用PI控制实现直流侧输出电压平衡[3-5],但由于级联H桥整流器本身的非最小相位系统特性,其控制复杂,采用PI算法时,当系统不稳定或受到扰动时存在超调量大、且母线电压波动大等问题.而滑模变结构控制具有快速响应、抗干扰能力强、实现简单等优点,而在非线性系统中得到了广泛的应用[6].对于级联变流器的电压平衡调制,目前多采用基于独立电压环的补偿控制方法,但其存在结构复杂、收敛速度慢等问题[7-8],而二维调制具有平衡效果好、恢复快等优点[9].因此本文将滑模变结构应用于级联整流器的控制中,并结合基于二维调制的电压调制方式,实现系统的快速响应和强抗干扰性能.
1 级联H桥整流电路的拓扑结构无工频变压器级联式功率变换器单相拓扑结构如图 1所示,包括整流级、高频DC-DC变换和逆变级3部分组成,其中整流级与逆变级均采用H桥级联式的结构,该结构能在交流侧输出较高电压阶梯波的同时,使单个功率器件承受的电压降低,实现了较低耐压等级的功率器件应用于较高电压等级的功率变换场合[10-11].级联H桥逆变器结构简单,易于模块化,已广泛应用于高压电气传动、大功率静止无功补偿、大功率有源电力滤波等场合[12-14].但目前对该变换器的级联整流侧的研究还很少,同时级联型整流器的研究是这种新型无工频变压器级联式功率变换器成败的关键.
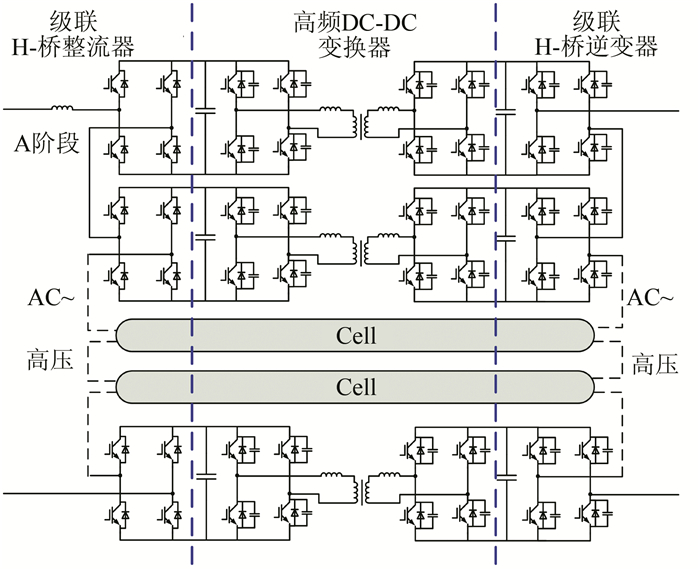
|
| 图 1 单相级联H桥高压大功率变换器拓扑结构 Figure 1 Topology of single phase cascaded H bridge high voltage and high power converter |
基于此,本文对该两级级联式功率变换器级联整流侧的电压均衡控制策略进行了研究.
1.1 两级级联H桥整流电路的数学模型两级级联H桥整流器的拓扑结构如图 2所示.
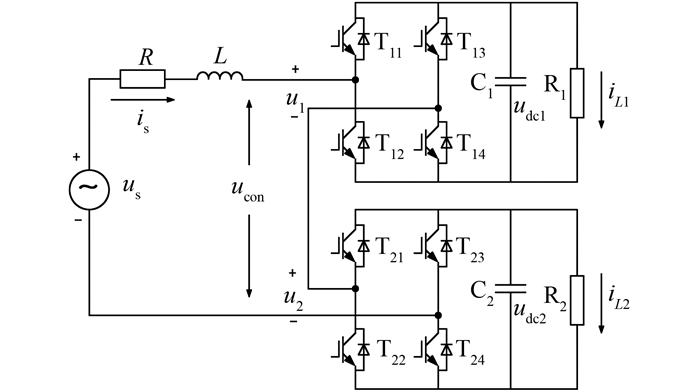
|
| 图 2 单相两级级联H桥整流电路拓扑结构 Figure 2 Topology of single-phase 2 H bridges cascaded rectifier circuit |
单相H桥PWM整流器的输入端通过H桥级联的形式连接起来,并通过一个电感L和电阻R接入电网.定义开关Tij (i=1,2;j=1,2,3,4)导通时为“1”,关断时为“0”,并且同一桥臂两个开关管开关状态相反,可以将各桥臂上管的开关状态定为单级PWM整流器的开关状态.
系统的基于占空比的数学模型如下:
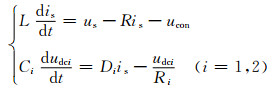 (1)
(1)
式中:udci为两H桥直流侧输出电压;Ci为两桥直流侧电容;Di为两桥各自的占空比,ucon=d1udc1+d2udc2.
令D1+ D2=D、udc1+udc2=udc、C1=C2=C,则式(1)可简化为
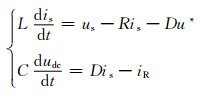 (2)
(2)
式中:u*为两桥处于稳态时每个桥的直流侧电压给定值.
1.2 级联型PWM整流电路的单相坐标变换为了实现单相PWM整流器到两相同步d-q旋转坐标系下的坐标变换,需构造一个与电流is(t)垂直的虚拟量iv(t),在坐标系中构成α-β两相静止坐标系[15].令
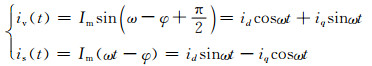
根据坐标变换理论,两相静止到两相同步旋转坐标系的变换为
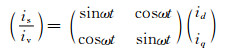
其反变换为
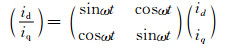
所以整流器交流侧电压:
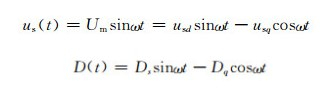
联立式(2)及以上各式得:
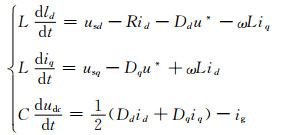 (3)
(3)
式中:usd、usq为输入电源电压us在两相旋转d-q坐标系下的d轴和q轴分量.
2 级联H桥整流器电容电压平衡控制 2.1 基于滑模控制的电压外环设计滑模控制主要根据系统正常运行阶段的动态品质要求来设计,滑模变结构控制策略设计主要包括两方面:一是根据系统的动态特性,建立合适的滑模切换函数s(x);二是设计控制律使滑动模态在有限时间内能够稳定到达滑模面s(x)=0上,求取控制函数μ(x,t)使系统状态点尽量存在于滑模面上.控制函数μ(x,t)可由下式表示:
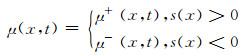
滑模控制系统通过判断滑模函数s(x)符号来切换控制量改变系统结构,使系统状态变量运动到所设计的空间面s(x)=0上,以实现系统所要达到的动态特性.
滑模面函数s(x)中的x一般选为系统状态变量的偏差来获得较好的控制效果.级联型PWM整流器的控制目的是为了实现对直流侧电压的控制,获得单位功率因数即iq=iq*=0,将直流侧总电压的误差作为滑模控制器的输入指令,输出网侧电流的有功分量.将实际值与参考值之间的误差作为新的状态变量,即定义误差变量:
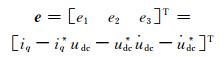 (4)
(4)
选择滑模面函数为
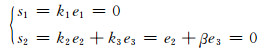 (5)
(5)
将式(3)、(4)代入式(5)化简整理得:
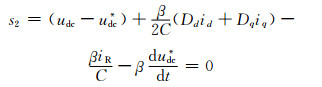
系统控制的主要问题就是使其状态轨迹在设定的滑模面上进行滑动,由于滑模函数中含有非线性时变量Dd和Dq.然而在d-q同步旋转坐标系下usd、usq和稳态时Dd和Dq为常数,根据理想滑模面是s1=0与s1的一阶导数等于0和式(2)以及理想状态下各个量的值、功率平衡原理可以得出:
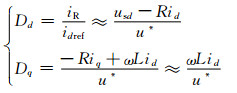 (6)
(6)
将式(6)代入s2=0整理得:
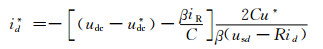
同时理想滑模面可以改写为
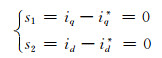 (7)
(7)
根据滑模变结构原理,滑模可达性条件仅保证由状态空间任意位置运动点在有限时间内到达切换面的要求,而对于趋近运动的具体轨迹未作任何限制,采用趋近律的方法可以改善趋近运动的动态品质.指数趋近律的滑模控制表达式如下:
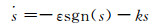
式中:ds(x)/dt=-ks, 为指数趋近项.
指数趋近中,趋近速度从一较大的值逐步减小到零,不仅缩短了趋近时间,而且使运动点到达切换面时的速度很小.对单纯的指数趋近,运动点逼近切换面是一个趋近过程,不能保证有限时间内到达,切换面上也就不存在滑模动态了,所以要增加一个等速趋近项ds(x)/dt=-εsgn(s),使当s趋近于零时,趋近速度是ε而不是零,可以保证有限时间内到达.为了保证快速趋近的同时削弱斗振,应在增大k的同时减小ε.令
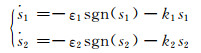 (8)
(8)
联立级联整流器dq坐标系下电流状态方程(3)及(7)、(8)可得:
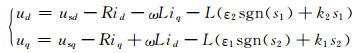 (9)
(9)
式中:ud=ddu*;uq=dqu*.
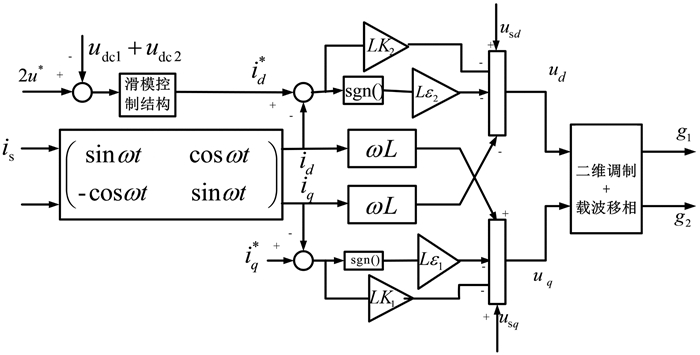
系统的控制结构框图如图 3所示.
|
| 图 3 系统控制结构框图 Figure 3 Control structure diagram of system |
两桥交流侧电压u1、u2在任意一个开关周期内的平均值U1、U2均可取[-udci,udci]内的任意值,将两者分别作为二维平面的横轴和纵轴,由U1、U2合成ucon的调制区域如图 4(a)中虚线框所示, β曲线是在该区域内所有与横轴成135°的斜线,可以选择该β曲线上的任意调制点来合成这个ucon,同一条β曲线上的所有调制点所对应的ucon全部相等.当每条β曲线都选择中点作为调制点时,这所有中点的连线与横轴成45°,称此曲线为α平分曲线.
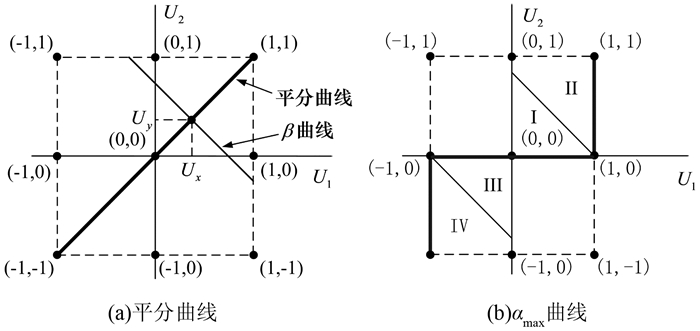
|
| 图 4 二维调制平面 Figure 4 Two-dimensional plane |
当两桥直流母线电压相等时采用平分曲线能够使两桥获取相等的有功功率,当负载发生突变或其他干扰发生时,假设udc1<udc2,该平分曲线是无法使两桥直流侧输出电压再次达到平衡状态,其恢复时间由电容吸收的有功能量决定,若想再次达到平衡,桥1需尽可能多地吸收有功能量,同时减少桥2有功能量的吸收.当为了最大限度地加快两桥的电压平衡速度,在二维控制平面中α曲线的轨迹将朝直流侧电容电压低的桥1靠近,限制的极限情况如图 4(b)所示的粗线轨迹,称此占空比分配曲线为αmax曲线,在该曲线调制下不同扇区内两桥的调制比如表 1所示.
| 调制区间 | D1 | D2 |
| Ⅰ | Ucon/udc1 | 0 |
| Ⅱ | 1 | (Ucon-udc1)/udc2 |
| Ⅲ | Ucon/udc1 | 0 |
| Ⅳ | -1 | (Ucon+udc1)/udc2 |
系统仿真参数为:单相正弦输入电压310 V,频率50 Hz;输出直流电压参考值200 V,输入电感为10 mH,线路等效阻抗为0.5 Ω,直流侧电容为2 200 μF,开关频率为5 kHz.在基于二维调制的电压平衡控制下,为了验证滑模控制策略具有较好的静动态性能,与电压电流双PI控制进行了对比,各仿真下的参数设置如表 2和表 3所示.
| 滑模控制下参数 | 数值 |
| 电压滑模系数β | 0.007 |
| 电流id趋近律系数K1 | 8 000 |
| L1 | 0.05 |
| 电流iq趋近律系数K2 | 8 000 |
| L2 | 0.05 |
| 双PI控制下参数 | 数值 |
| 电压环KvP | 0.1 |
| 电压环KvI | 5 |
| 电流id环KIdp | 80 |
| 电流iq环KIdq | 80 |
图 5是系统启动过程中基于二维调制下滑模控制和电压电流双PI控制时的直流侧输出电压波形.从图中红色波形可以看出滑模控制下,直流侧电容电压进入稳定的调整时间为0.03 s,并且电压最大超调量为1.5%;蓝色波形可以看出PI控制下直流侧电容电压进入稳定的调整时间为0.15 s,电压最大超调量为12.5%;由此可以看出启动过程滑模控制比PI控制调整时间减少了0.12 s,电压最大超调量降低了11%.
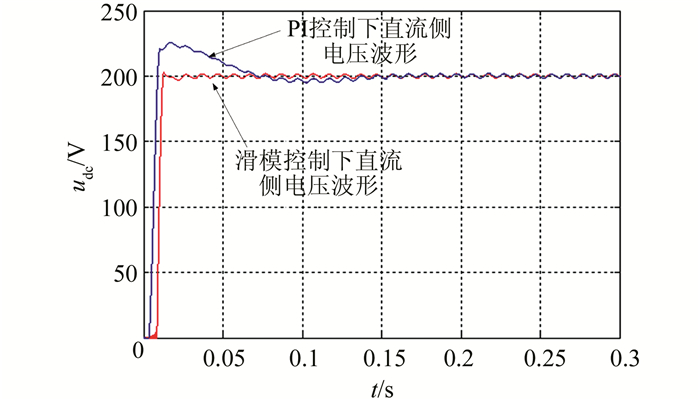
|
| 图 5 两种控制下直流侧电压启动响应波形 Figure 5 DC voltage waveform of startup response under two controls |
图 6是基于滑模控制下系统稳定时的交流侧电压电流波形,实现单位功率因数.
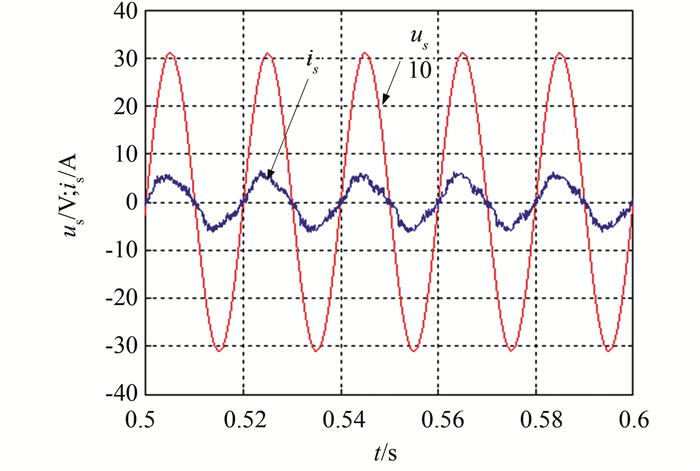
|
| 图 6 滑模控制下整流器交流侧电压电流波形 Figure 6 The AC input current of the rectifier under sliding mode control |
仿真时,用负载变化来模拟整流侧后级电路的扰动,观察两桥的直流侧输出电压的动态过程.图 7为系统两种控制下负载增减时的动态调整波形,为桥1的直流侧负载在1 s时由100 Ω升高到220 Ω,同时在1.5 s时又恢复到100 Ω时直流侧输出电压变化波形.从图 7(a)中看出,采用滑模控制时,桥1和桥2电压几乎无波动.图 7(b)中电压电流双PI控制下的动态调整时间为0.1 s,桥1和桥2电压上下波动量为5 V,占稳定电压的2.5%, 说明在桥1负载突变的动态过程中滑模控制与电压电流双PI控制相比,反应迅速,电压几乎无波动.
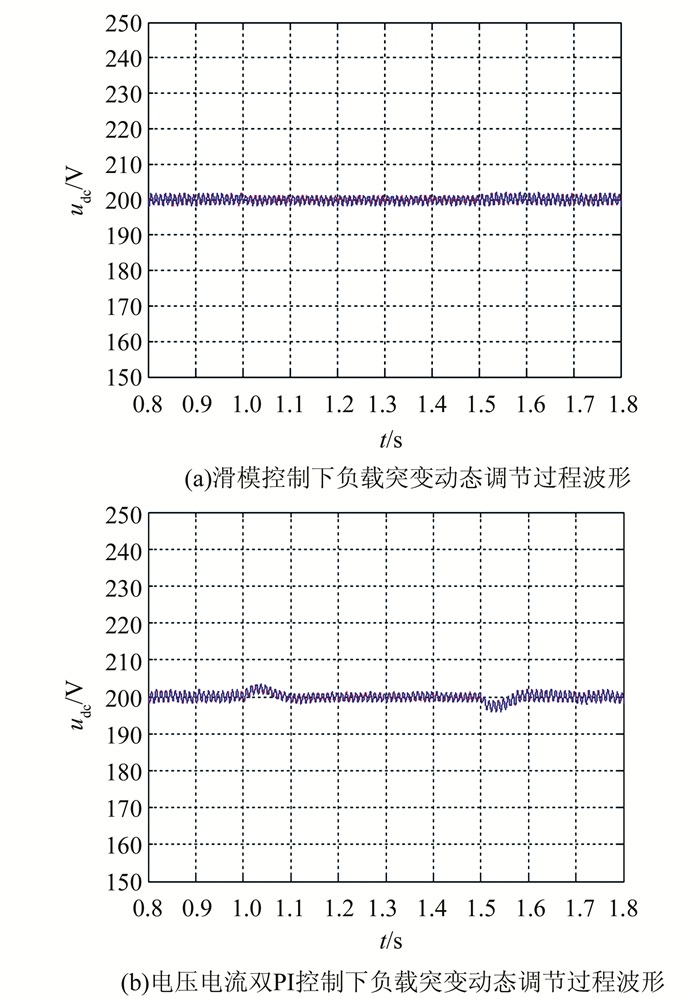
|
| 图 7 两种控制下负载突变动态调节过程波形 Figure 7 Dynamic adjustment process waveform of mutation load under two control |
RT-lab是由加拿大Opal-RT Technologie公司推出的一套工业级的系统实时仿真设备,是一种全新的基于模型的工程设计应用平台.通过RT-lab,工程师可以直接将Matlab-Simulink环境下建立的系统数学模型应用于实时仿真、控制、测试以及其他相关领域,在该平台上实现工程项目的设计、实时仿真、快速原型与硬件在回路测试.
本文搭建了基于RT-lab的半实物实时仿真平台来验证本控制的有效性.控制电路经RT-lab来产生开关控制信号,然后经RT-lab数字量输出板卡输出开关信号,并输入主电路中控制IGBT的动作.主电路采用英飞凌F4-150R12KS4的IGBT模块;型号QP12W05S-37A的金升阳驱动模块;电流检测回路采用型号为SE1T50C50V6SP9的霍尔传感器,其额定输入为50 A,额定输出为50 mA,在其输出端串联一个100 Ω的电阻就可将信号转化为额定输出为5 V的电压信号.控制电路采用滑模控制和二维调制相结合的控制方法产生控制信号.
实验参数设置:交流侧电压有效值Us=220 V,频率50 Hz;交流侧电感L=10 mH;直流侧电容C1=C2=C=2 200 μF;直流侧输出参考电压为200 V;开关频率5 kHz.开始时负载R1=R2=100 Ω,到系统稳定运行的某一时刻使桥1的负载突变至220 Ω,桥2负载不变.
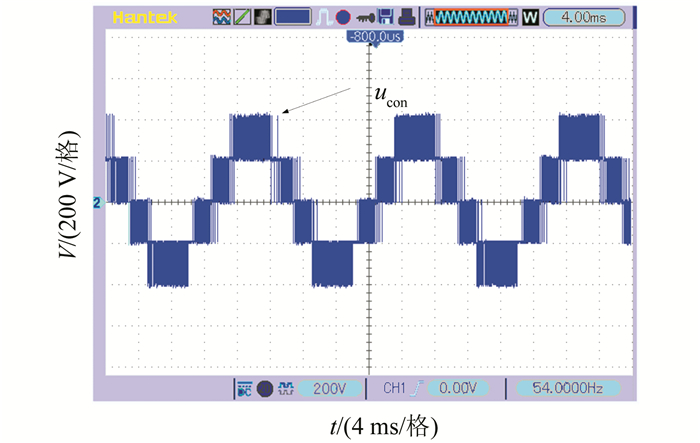
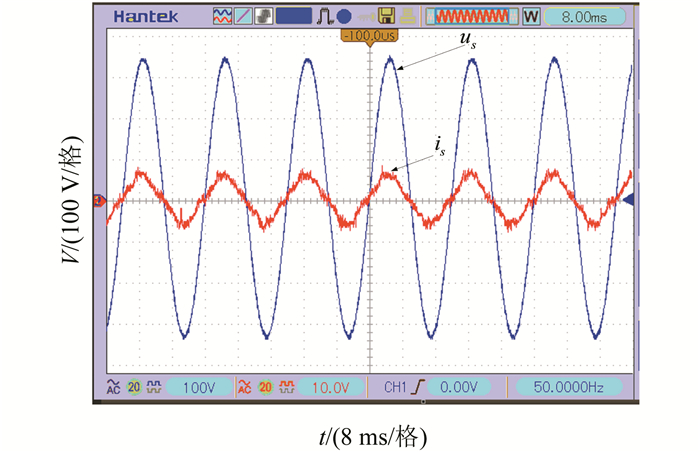
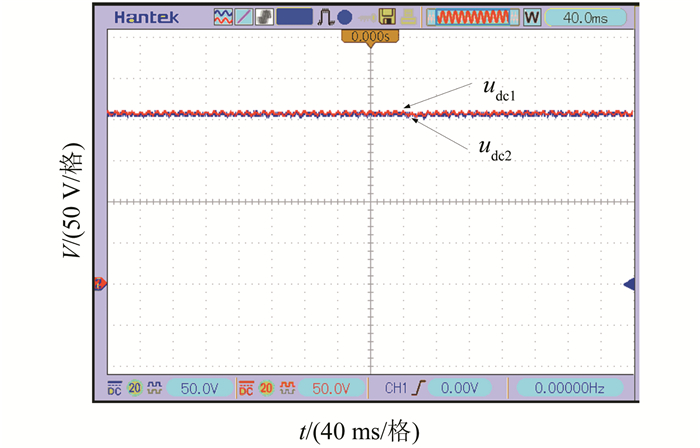
系统稳定运行时,交流侧电压、电流和直流侧电压波形如图 8、9、10所示:系统实现了交流侧五电平阶梯波与单位功率因数;两桥直流侧母线电压在0.03 s时均达到稳定状态.
|
| 图 8 级联整流器交流侧电压 Figure 8 AC input voltage of rectifier |
|
| 图 9 级联整流器交流侧输入电流 Figure 9 AC input current of rectifier |
|
| 图 10 级联整流器直流侧输出电压 Figure 10 DC output voltages of rectifier |
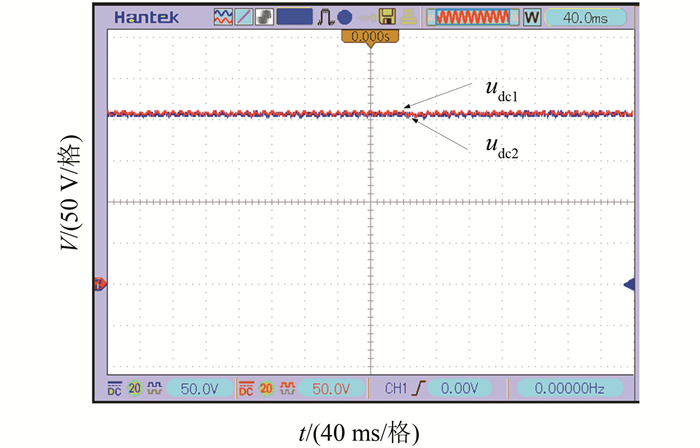
图 11所示为基于滑模控制的系统负载突变时的动态调节过程,图中显示了滑模控制下桥1负载由100 Ω突变为220 Ω时的各桥直流侧电容电压的动态变化过程,基本无波动,与仿真一致.
|
| 图 11 滑模控制下桥1负载突变时系统动态过程 Figure 11 System dynamic process of the bridge 1 load mutation under sliding mode control |
本文通过对级联H桥整流器的拓扑结构分析,建立了单相两桥级联整流器同步坐标系下的数学模型,采用滑模控制策略和二维调制策略,实现各桥直流侧母线电压平衡控制.仿真和实验验证了所提出的控制策略在系统启动和直流侧负载突变时具有更好的动静态性能,实现了网侧功率因数为1以及高性能的输出电压.本文研究结论同样适用于多级联H桥整流电路的控制,为无工频变压器级联式功率变换器和双H桥级联式变频器提供了理论基础,具有一定的研究价值和应用前景.
| [1] | Marzoughi A, Iman-Eini H. Indirect control for cascaded H-bridge rectifiers with unequal loads[C]// 2012 3rd Power Electronics and Drive Systems Technology (PEDSTC 2012), 2012: 92-97. |
| [2] |
尹相卿. 新一代电压平衡控制大功率级联H桥整流器[J].
工矿自动化, 2013, 39(11): 23–27.
Yin Xiangqing. A new generation of high-power cascaded H-bridge rectifier for voltage balancing control[J]. Industry and Mine Automation, 2013, 39(11): 23–27. |
| [3] |
郑征, 李斌, 胡丹丹. 基于二维调制的级联型H桥PWM整流器电压平衡控制策略[J].
河南理工大学学报(自然科学版), 2013, 32(2): 199–204.
Zheng Zheng, Li Bin, Hu Dandan. Voltage balancing control strategy for cascaded H-Bridge PWM rectifier based on two dimensional modulation[J]. Journal of Henan Polytechnic University (Natural Science), 2013, 32(2): 199–204. |
| [4] | Zhang Guopeng, Cheng Hong, Cheng Long, et al. A fast voltage balance curve of duty cycle distribution for cascaded rectifier stage based on two dimensional modulation[C]//IEEE Power Engineering & Automation Conference, 2011: 71-74. |
| [5] | Antonio Dell'Aquila, Marco Liserre, Vito G. Monopoli, Paola Rotondo. Overview of PI-based solutions for the control of the dc-buses of a single-phase H-bridge multilevel active rectifier[J]. Applied Power Electronics Conference and Exposition, 2004, 19(2): 836–842. |
| [6] | Kaletsanos A X, Manolas I S, Pavlou K G, et al. Sliding mode control for cascaded H-bridge boost rectifiers[C]//IEEE, 2010: 1070-1075. |
| [7] |
陶兴华, 李永东, 孙敏. 一种H桥级联型PWM整流器的直流母线电压平衡控制新方法[J].
电工技术学报, 2011, 26(8): 85–90.
Tao Xinghua, Li Yongdong, Sun Min. A novel DC-link voltages balancing control method for cascaded H-bridge rectifier[J]. Transactions of China Electrotechnical Society, 2011, 26(8): 85–90. |
| [8] |
杨荣, 王聪, 张国澎. 基于整体能量分配的级联整流级电压平衡控制的研究[J].
电源世界, 2011(11): 31–35.
Yang Rong, Wang Cong, Zhang Guopen. The voltage balance control research for cascaded H-bridge rectifier based on integral power distribution[J]. The World of Power Supply, 2011(11): 31–35. |
| [9] |
郑征, 李绍令. 基于二维调制的级联型整流器控制策略研究[J].
电力电子技术, 2015, 7(49): 92–96.
Zheng Zheng, Li Shaoling. The control strategy research for cascaded H-bridge PWM rectifier based on two dimensional modulation[J]. Power Electronics, 2015, 7(49): 92–96. |
| [10] |
高志刚, 冬雷, 李永东, 等. 基于高频变压器的背靠背级联H桥型变换器[J].
电工技术学报, 2013, 28(6): 133–138.
Gao Zhigang, Dong Lei, LI Yongdong, et al. Research on back to back cascaded H-bridge converter based on high frequency transformer[J]. Transactions of China Electrotechnical Society, 2013, 28(6): 133–138. |
| [11] |
周彬倩, 李文意, 杨民京, 等. 基于单相背靠背H桥级联结构的仿真研究[J].
陕西电力, 2014, 42(4): 41–44.
Zhou Binqian, Li Wenyi, Yang Minjing, et al. Simulation study on single-phase back to back H-bridge cascade structure[J]. Shaanxi Electric Power, 2014, 42(4): 41–44. |
| [12] | Iman-Eini H, Farhangi Sh, Schanen J L. A modular AC/DC rectifier based on cascaded H-bridge rectifier[C]// 13th International Power Electronics and Motion Control Conference (EPE-PEMC 2008), 2008: 173-180. |
| [13] |
田铭兴, 阎宏, 赵雨欣. 级联H桥SVG直流侧电容电压平衡控制方法[J].
电网技术, 2013, 37(9): 2632–2638.
Tian Mingxing, Yan Hong, Zhao Yuxin. A balancing control method of DC capacitor voltage for cascaded H-bridge SVG[J]. Power System Technology, 2013, 37(9): 2632–2638. |
| [14] |
顾春阳, 郑泽东, 李永东. 用于机车牵引的新型级联H桥整流器电压平衡方法[J].
电工技术学报, 2013, 28(12): 168–172.
Gu Chunyang, Zheng Zedong, Li Yongdong. A novel voltage balancing method of cascaded H-bridge rectifiers for locomotive traction applications[J]. Transactions of China Electrotechnical Society, 2013, 28(12): 168–172. |
| [15] | Miranda U A, Aiedes M, Rlim L G B. A DQ synchronous reference frame current control for single-phase converters[C]// Power Electronics Specialists Conference, 2005: 1377-1381. |
 2018, Vol. 51
2018, Vol. 51



