文章信息
- 梁姗姗, 吴军, 刘涤尘, 董飞飞, 胡静竹, 章杨帆, 韩翔宇
- LIANG Shanshan, WU Jun, LIU Dichen, DONG Feifei, HU Jingzhu, ZHANG Yangfan, HAN Xiangyu
- 基于曲面拟合的电力系统节点动态频率响应特性的影响因素
- Analysis of factors influencing nodal dynamic frequency response characteristics based on curved surface fitting
- 武汉大学学报(工学版), 2017, 50(2): 228-232,238
- Engineering Journal of Wuhan University, 2017, 50(2): 228-232,238
- http://dx.doi.org/10.14188/j.1671-8844.2017-02-011
-
文章历史
- 收稿日期: 2016-05-10
电力系统频率是电力系统很重要的一个参数,是衡量电力系统电能质量和安全稳定性的重要指标之一[1].目前国内外电力系统关于节点动态频率响应特性的研究主要集中在系统故障节点的频率变化、系统平均频率变化的识别和静态频率特性的计算, 而对系统节点动态频率特性的研究较少[2-4].
静态频率特性记录的是暂态平息后的准稳态值,实际上在暂态过程中系统各节点的频率变化是非同步的,同时识别出的系统静态频率特性系数只是一个粗糙的数值范围,无法快速反映不同初始运行方式及扰动状态下节点的动态频率响应特性,难以在系统保护及紧急控制等快速过程中得到应用[5-7], 因此有必要对电网适应多变量的节点频率响应特性识别与预测方法及变化趋势进行研究[8].
本文综合考虑初始运行方式、故障形式及地点对观测节点动态频率特性的影响, 基于离线仿真提取的有限采样点,运用改进的拟合方法得到多变量的空间曲面,同时对仿真值和拟合值的误差进行分析,较传统识别与计算方法在计算的快速性、简便性及准确性方面均有本质性的提高,具有十分重要的理论和工程应用价值.
1 节点动态频率响应特性 1.1 定义电力系统节点频率特性指的是对于电力系统中某一观测点,当观测点周围的观测空间发生功率扰动ΔP时,功率扰动ΔP与系统初始功率P0的比值和最大频率偏差Δf与系统初始频率f0比值之比,系统功频特性系数K:
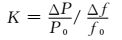 (1)
(1)
式中:P0、f0分别为正常运行时系统的功率和频率.
1.2 主要影响因素影响复杂系统频率动态特性的重要因素主要包括初始平衡功率P0、功率扰动ΔP和电气距离S[9-15].
改变电力系统初始运行状态主要是指改变系统的P0值;系统中扰动形式诸多,本文以发电机扰动为例, 对K与ΔP的变化关系进行分析;功率扰动发生在不同地点,会改变电网的运行方式,这种特性可以由电力系统中电气距离这一重要指标衡量.
选定观测点后,电气距离的改变可以通过切除不同发电机来实现,一般通过2点之间转移电抗的大小来表征.本文通过求取系统的节点阻抗矩阵间接求取2点间的转移阻抗,求取方法:
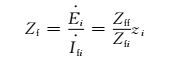 (2)
(2)
式中:Zf为转移阻抗; Zff为观测点的自阻抗; Zfi为观测点与扰动点的互阻抗; Zi为扰动点发电机的次暂态阻抗.
1.3 基于曲面拟合的频率特性系数预测本文提出了一种既不影响电力系统正常运行又能准确地求取K值的方法,即运用PSASP求取不同条件下的K值,然后运用MATLAB拟合出不同平衡功率分别对应的三维坐标系(K、S、ΔP)下的空间曲面,使得节点动态频率响应特性在任意状态下均对应曲面上的一个矢量点,从而预测任意ΔP、S对应的K值.
1.3.1 PSASP的仿真方法基于PSASP的EPRI-36节点模型,通过切除发电机来造成有功扰动,再记录频率变化,取频率变化的最大值作为Δf,代入式(1) 中,计算出不同P0对应的不同扰动点和ΔP下的K值,最后利用计算结果进行曲面拟合.
1.3.2 曲面拟合方法为精确计算不同ΔP和S条件下的K值,运用插值和拟合方法做精确的数据处理,并利用改进的B样条法对由PSASP获得的有限个数据点所拟合出的不光滑曲面进行修正.基于MATLAB 3次样条插值拟合法,对节点动态频率响应特性进行曲面拟合.最后对拟合的频率特性系数曲面进行误差分析,验证方法的有效性.
1.3.3 频率特性系数预测通过MATLAB的程序编写,得到不同P0、ΔP和S条件下K值拟合曲面,从而实现多变量条件下系统频率特性系数的识别与计算.在系统功率扰动导致频率变化时,拟合出的(K、S、ΔP)三维曲面可为调度部门提供处理参考.
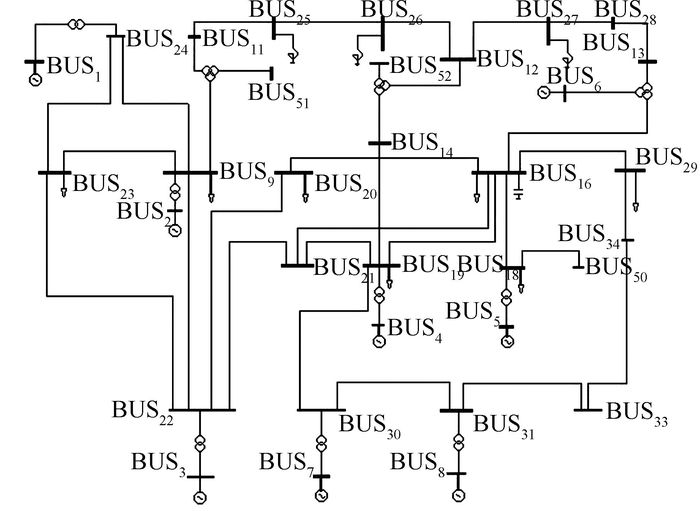
1.4 节点频率特性影响因素仿真分析 1.4.1 仿真计算模型实验所用EPRI-36系统单线图如图 1所示.
|
| 图 1 纯交流系统单线图 Figure 1 Pure AC system single-line diagram |
本次仿真,采用1号潮流作业,本模型的基准值为100 MVA,BUS1可视作平衡机,BUS6作为调相机.通过计算可得,该系统在扰动前的总有功发电P0=26.537 1.
1.4.2 仿真实验变量设定原则在改变系统初始运行状态时需同步按半分比减少发电机出力和负荷.初始运行状态的改变量不宜过大,以不超过系统初始功率的10%为宜;为避免造成频率失稳,电力系统频率变化量不应超过0.5 Hz;由于功率扰动过大会导致系统失稳,ΔP应控制在一定范围内.
1.4.3 仿真方法在潮流计算中始终保持系统和实验监测节点BUS2的有功和无功输出的比例不变.确定初始运行状态、扰动点和扰动量后,由公式ω=2πf可知,ω和f的标幺值变化等值,故BUS2处的f变化可间接由其ω变化得出.
选取BUS3、BUS8和BUS7为切机点;设定切机量为0.1、0.2、0.3和0.4;P0分别设置为初始运行功率的0.95和1.05倍.
确定了观测点与扰动点后,根据本次仿真数学模型以及发电机和线路参数,即可利用式(2) 计算出观测点与扰动点的电气距离S,其计算结果如表 1所示.
| 扰动中心 | 转移阻抗 | 电气距离S/m |
| BUS3 | 0.021 0 + 0.507 6i | 0.507 6 |
| BUS4 | 0.018 3 + 0.568 5i | 0.568 5 |
| BUS5 | 0.028 9 + 0.601 0i | 0.601 0 |
| BUS8 | 0.065 7 + 0.750 3i | 0.750 3 |
| BUS7 | 0.084 9 + 0.969 95i | 0.969 9 |
以初始运行功率下扰动点为BUS3,扰动量为0.1为例,通过暂态稳定计算得到BUS2处发电机角速度ω的变化曲线,通过数据分析得出曲线最低点的角速度ω的标幺值为0.997 3,故Δω为0.002 7,即Δf为0.002 7,故由式(1) 得:K=4.326 6.
依此方法分别将扰动点设定在BUS3、BUS8和BUS7处,且每处的扰动量分别设置为0.1、0.2、0.3和0.4,即可得出电力系统为初始潮流时的结果,如表 2所示.
| 扰动点 | S | ΔP=0.1 | ΔP=0.2 | ΔP=0.3 | ΔP=0.4 | ||||
| ω | K | ω | K | ω | K | ω | K | ||
| BUS3 BUS8 BUS7 | 0.507 6 0.750 3 0.969 9 | 0.997 3 0.997 3 0.997 8 | 4.326 6 4.286 6 3.836 5 | 0.995 5 0.995 6 0.996 5 | 5.169 5.229 5 4.831 2 | 0.993 6 0.993 9 0.995 3 | 5.467 3 5.661 7 5.355 0 | 0.991 7 0.992 1 0.994 | 5.629 8 5.868 2 5.652 5 |
按照以上步骤,将各台发电机的输出功率分别减小5%和增大5%,分别将扰动点设定在BUS3、BUS8和BUS7处,设定扰动量为0.1、0.2、0.3和0.4,即可得出不同初始运行条件下,不同扰动点和不同扰动量对应的K值,结果如表 3、4所示.
| 扰动点 | S | ΔP=0.1 | ΔP=0.2 | ΔP=0.3 | ΔP=0.4 | ||||
| ω | K | ω | K | ω | K | ω | K | ||
| BUS3 BUS8 BUS7 | 0.507 6 0.750 3 0.969 9 | 0.997 9 0.997 9 0.998 2 | 5.552 2 5.586 4 4.723 8 | 0.996 7 0.996 8 0.997 4 | 7.015 0 7.182 6 6.466 1 | 0.995 3 0.995 6 0.996 6 | 7.509 7 7.813 5 7.393 8 | 0.993 7 0.994 1 0.995 7 | 7.473 7 7.813 5 7.818 7 |
| 扰动点 | S | ΔP=0.1 | ΔP=0.2 | ΔP=0.3 | ΔP=0.4 | ||||
| ω | K | ω | K | ω | K | ω | K | ||
| BUS3 BUS8 BUS7 | 0.507 6 0.750 3 0.969 9 | 0.995 3 0.995 3 0.995 8 | 2.461 1 2.455 3 2.011 7 | 0.993 3 0.993 5 0.994 5 | 3.485 3 3.541 1 3.061 3 | 0.991 2 0.991 5 0.993 1 | 3.977 6 4.070 0 3.695 0 | 0.988 6 0.988 6 0.991 7 | 4.084 6 4.209 1 4.062 1 |
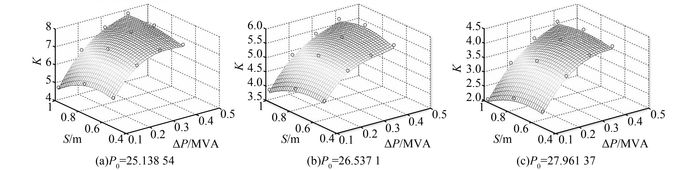
运用处理表 2数据同样的方法分别处理表 3、4中的数据,得到如图 2所示的不同初始平衡功率下的频率特性系数拟合曲面.
|
| 图 2 P0=25.138 54/26.537 1/27.961 37时的3次样条插值曲面 Figure 2 Cubic spline interpolation surfacewhenP0=25.138 54/26.537 1/27.961 37 |
拟合曲面的变化趋势:曲面整体上变化较平滑;沿着表征功率扰动的X轴呈逐渐上升趋势;沿着表征电气距离的Y轴呈先增大后减小的趋势且变化较平缓;纵向对比3个曲面,随着初始平衡功率的不断增大,表征频率特性系数的Z轴不断减小,并且曲面沿着X轴的变化陡度越来越大.
1.5.2 拟合结果精确度的校验根据已有的数据运用Matlab拟合曲面,为了验证实验的精确性,需要对拟合的频率特性系数曲面进行误差分析.误差是指拟合值K1和仿真值K1′之间的误差:
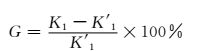 (3)
(3)
电气距离S=0.600 978,P0=26.537 1时,对不同ΔP下的K值进行精度校验.然后设定ΔP=0.25,对不同的电气距离下的K值再次进行精度的校验.
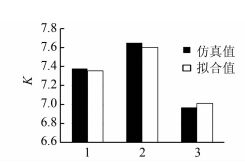
功率基准值皆为100 MW, 由式(3) 得到相对应的误差,对仿真值和拟合值进行误差对比分析,得出图 3~8的分析结果.
|
| 图 3 P0=25.138 54, ΔP=0.25时的K值对比图 Figure 3 K comparison chart when P0=25.138 54, ΔP=0.25 |
|
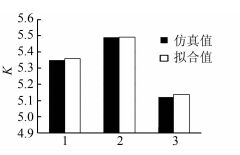
| 图 4 P0=26.537 1, ΔP=0.25时的K值对比图 Figure 4 K comparison chart when P0=26.537 1, ΔP=0.25 |
|
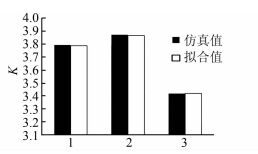
| 图 5 P0=27.961 37, ΔP=0.25时的K值对比图 Figure 5 K comparison chart when P0=27.961 37, ΔP=0.25 |
|
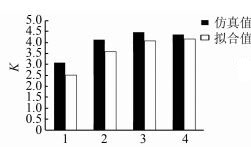
| 图 6 P0=27.96137, S=0.600 978时的K值对比图 Figure 6 K comparison chart when P0=27.96137, S=0.600 978 |
|
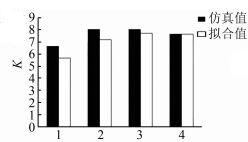
| 图 7 P0=25.138 54, S=0.600 978时的K值对比图 Figure 7 K comparison chart when P0=25.138 54, S=0.600 978 |
|
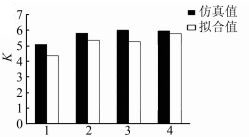
| 图 8 P0=26.537 1, S=0.600 978时的K值对比图 Figure 8 K comparison chart when P0=26.537 1, S=0.600 978 |
1) 在相同的初始平衡功率P0和电气距离S的条件下,功率扰动ΔP越大K值越大.说明扰动越大,最大频率偏移越大,从而表征扰动对系统影响越大.
2) 电气距离对频率特性系数无明显影响,原因是采用的是36节点简单电力系统,电气距离只能在很有限的范围内变动.
3) 在相同的功率扰动ΔP和电气距离S的条件下,初始平衡功率P0越大,频率特性系数越小,说明初始平衡功率越大,系统对扰动的调节作用越强,则相同的扰动对电力系统的影响越小.
4) 观察图 3~5,并对具体数值进行计算可得,在相同的初始平衡功率P0和功率扰动ΔP的条件下,仿真结果和拟合值的误差能够控制在1%以内;观察图 6~8,并对具体数值进行计算可得,在初始平衡功率P0和电气距离S相同的条件下,功率扰动ΔP较大时误差均能控制在10%以内,证明通过曲面拟合确定系统功频特性系数的方法有效可行.
3 结论本文采用曲面拟合的方法对仿真计算得到的频率响应特性系数进行拟合,得到以下结论:
1) 通过曲面拟合确定系统功频特性系数的方法有效可行,拟合计算结果较理想,能较好地反应实际K值,误差在允许范围内.
2) 在实际操作中遇到例如切机的紧急情况时,需要电力系统此时的K值以调整负荷,本文所拟合出的曲面可供参考, 可以得到所需K值,具有较高的参考价值.
3) 曲面拟合能更直观地反映节点频率特性与影响因素之间的关系,并验证了理论分析的正确性.
4) 可以用采样点反求法对节点动态频率响应特性变化、频率偏差和频率稳定性变化及其趋势进行预测.
本文仿真采用的EPRI-36节点模型与真实的电力系统之间存在差距.在条件允许的情况下,为了缩减与真实电力系统的差别,可以采用更复杂的节点模型;本文运用了3种插值拟合方法,若条件允许,可以采用更多种曲面拟合方法对数据进行处理并选取更适合的曲面拟合方法.
| [1] |
韩民晓, 崔军立, 姚蜀军, 等. 大量风电引入电网时的频率控制特性[J].
电力系统自动化, 2008, 32(1): 29–33.
Han Minxiao, Cui Junli, Yao Shujun, et al. Frequency control characteristics for a power system with large amounts of wind power[J]. Automation of Electric Power Systems, 2008, 32(1): 29–33. |
| [2] |
赵强, 王丽敏, 刘肇旭, 等. 全国电网互联系统频率特性及低频减载方案[J].
电网技术, 2009, 33(8): 35–40.
Zhao Qiang, Wang Limin, Liu Zhaoxu, et al. Study on dynamic frequency characteristics and coordinative under-frequency load shedding scheme for nationwide interconnected power grid of china[J]. Power System Technology, 2009, 33(8): 35–40. |
| [3] |
周海锋, 倪腊琴, 徐泰山. 电力系统功率频率动态特性研究[J].
电网技术, 2009, 33(16): 58–62.
Zhou Haifeng, Ni Laqin, Xu Taishan. Study on power-frequency dynamic characteristic of power grid[J]. Power System Technology, 2009, 33(16): 58–62. |
| [4] |
吴军, 刘涤尘. 基于灰色预测的电力系统静态频率特性系数计算[J].
电力系统保护与控制, 2012, 40(6): 97–103.
Wu Jun, Liu Dichen. Calculation of the coefficient of static frequency characteristics of power system based on gray system forecast[J]. Power System Protection and Control, 2012, 40(6): 97–103. DOI:10.7667/j.issn.1674-3415.2012.06.018 |
| [5] |
董飞飞, 刘涤尘, 吴军, 等. 基于系统频率响应特性的"三华"电网交换容量极限计算[J].
电力自动化设备, 2012, 32(7): 104–107.
Dong Feifei, Liu Dichen, Wu Jun, et al. Calculation of exchange capacity limit based on system frequency response characteristics for "San-Hua" power grid[J]. Electric Power Automation Equipment, 2012, 32(7): 104–107. |
| [6] |
李爱民, 蔡泽祥. 基于轨迹分析的互联电网频率动态特性及低频减载的优化[J].
电工技术学报, 2009, 24(9): 171–177.
Li Aimin, Cai Zexiang. Frequency dynamics analysis and load shedding assessment based on the dynamic simulation trajectory of interconnected power system[J]. Transactions of China Electrotechnical Society, 2009, 24(9): 171–177. |
| [7] |
王茂海, 徐正山, 谢开, 等. 基于WAMS的系统自然频率特性系数确定方法[J].
电力系统自动化, 2007, 31(3): 15–18.
Wang Maohai, Xu Zhengshan, Xie Kai, et al. Selection of DC capacitance and schemes of self-excitation startup charge for the H-bridge cascading SSSC[J]. Automation of Electric Power Systems, 2007, 31(3): 15–18. |
| [8] |
张恒旭, 李常刚, 刘玉田, 等. 电力系统动态频率分析与应用研究综述[J].
电工技术学报, 2010, 25(11): 169–176.
Zhang Hengxu, Li Changgang, Liu Yutian, et al. Reviews on power system dynamic frequency analysis and its application[J]. Transactions of China Electrotechnical Society, 2010, 25(11): 169–176. |
| [9] |
张卫华, 苑津莎, 张铁峰, 等. 应用B样条理论改进的变压器三比值故障诊断方法[J].
中国电机工程学报, 2014, 34(24): 4129–4136.
Zhang Weihua, Yuan Jinsha, Zhang Tiefeng, et al. An improved three-ratio method for transformer fault diagnosis using B-spline theory[J]. Proceedings of the CSEE, 2014, 34(24): 4129–4136. |
| [10] |
易俊, 周孝信. 考虑系统频率特性以及保护隐藏故障的电网连锁故障模型[J].
电力系统自动化, 2006, 30(14): 1–5.
YI Jun, Zhou Xiaoxin. Cascading failure model of power grid considering frequency response characteristics and hidden failures[J]. Automation of Electric Power Systems, 2006, 30(14): 1–5. DOI:10.3321/j.issn:1000-1026.2006.14.001 |
| [11] |
雷宇. 现代电力系统中影响动态频率特性的因素分析[D]. 重庆: 重庆大学, 2002.
Lei Yu.Factors affecting the modern power system dynamic frequency characteristics[D]. Chongqing: Chongqing university, 2002. http://cdmd.cnki.com.cn/Article/CDMD-10611-2003031844.htm |
| [12] |
陈文略, 王子羊. 三次样条插值在工程拟合中的应用[J].
华中师范大学学报, 2004, 38(4): 54–58.
Chen Wenlue, Wang Ziyang. The application of cubic splines interpolation in the project fitting[J]. Journal of Central Chna Normal University, 2004, 38(4): 54–58. |
| [13] |
李春意, 崔希民, 何荣, 等. 开采沉陷预计中三维空间曲面拟合参数的研究[J].
采矿与安全工程学报, 2011, 28(3): 420–424.
Li Chunyi, Cui Ximin, He Rong, et al. Research on fitting parameters of 3D surface in mining subsidence prediction[J]. Journal of Mining & Safety Engineering, 2011, 28(3): 420–424. |
| [14] |
罗凯明, 李雪, 孙勇. 互联电网频率响应标准[J].
电力自动化设备, 2008, 28(5): 111–113.
Luo Kaiming, Li Xue, Sun Yong. Frequency response standard of interconnected power network[J]. Electric Power Automation Equipment, 2008, 28(5): 111–113. |
| [15] |
魏晖, 沈善德, 朱守真, 等. 系统自然频率特性系数的实测与计算[J].
电力系统自动化, 2001, 25(5): 49–52.
Wei Hui, Shen Shande, Zhu Shouzhen, et al. Survey and calculation of frequency character quotient of power system[J]. Automation of Electric Power System, 2001, 25(5): 49–52. |
 2017, Vol. 50
2017, Vol. 50




