文章信息
- 汤亮, 王亮, 龚发云, 李倩, 徐显金, 钱坤
- TANG Liang, WANG Liang, GONG Fayun, LI Qian, XU Xianjing, QIAN Kun
- 一种小模数外平动少齿差行星轮减速器的传动特性分析
- Transmission characteristics analysis of outside linkage small modules planetary gear reducer with small tooth difference
- 武汉大学学报(工学版), 2017, 50(5): 778-783
- Engineering Journal of Wuhan University, 2017, 50(5): 778-783
- http://dx.doi.org/10.14188/j.1671-8844.2017-05-023
-
文章历史
- 收稿日期: 2016-10-27
随着我国工业经济的发展和进步,一些特殊行业对减速器的微小型化要求越来越高,小模数少齿差传动也日益受到关注.模数小于或等1的齿轮被称为小模数齿轮.小模数渐开线少齿差行星传动由最原始的K-H-V型行星轮系演变而来,相比传统的圆柱齿轮传动机构和蜗轮蜗杆传动机构而言,其拥有大传动比、效率高、运转平稳、噪音低等优点,同时由于其模数小及独特的齿轮内啮合特性,使其拥有结构紧凑、体积小的特点.因此,小模数少齿差行星轮减速机构目前已广泛应用于国防航空航天、起重运输工程机械、冶金采矿、工业机器人等领域,受到了国内外学者的重视.
1960年,太原工学院朱景梓教授首次提出一种极具创新性的少齿差双曲柄传动结构,引起了极广泛的关注[1].刘丹[2]等人分析了小模数少齿差传动的啮合质量,同时对传动参数进行了优化设计;郑红梅[3]等人对N型少齿差减速器在传动过程中齿轮的啮合过程进行了研究,分析了其啮合力的周期性波动情况;罗庆生[4]等人改进了小模数少齿差齿轮的齿形设计和齿轮加工工艺;杨江兵[5-6]等人通过ABAQUS有限元软件对渐开线少齿差传动进行了动态接触分析,得到了其啮合过程中刚度变化曲线;唐德威[7]等通过多目标优化设计思想对小模数少齿差齿轮传动进行了承载能力分析和体积优化.
由于减速器传动结构形式多样,针对小模数的外平动少齿差行星轮减速器的传动特性进行研究的文献还是少有报道.本研究设计了一款双环板外平动式小模数少齿差行星轮减速器,目前已申请国家发明专利.为揭示其结构与传动特性的关系,并为规模化生产提供科学依据,本文通过ADAMS虚拟样机平台对其进行运动学和动力学仿真,并结合经典理论评估其可靠性和合理性,为少齿差行星轮减速器的设计、分析、制造提供理论依据与实验参考.
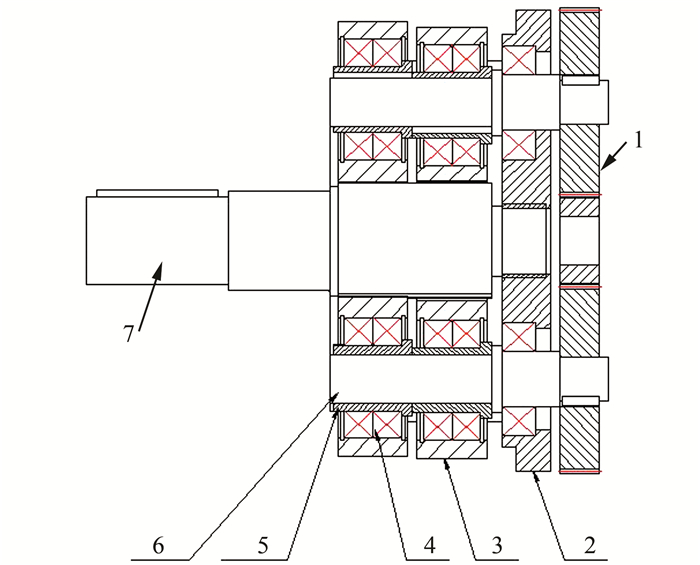
1 新型小模数少齿差行星轮减速器的基本结构及工作原理本研究设计的双环板外平动式小模数少齿差行星轮减速器的特点在于:区别于内平动少齿差传动中将内齿轮不动行星齿轮作为主动件,其由两块内齿板作为主动件啮合搓动外齿轮轴输出运动,提高了传动的平稳性和齿轮的啮合精度.基本结构如图 1所示,组成部件包括输入级行星轮系1,三根与输入轮系连接的恒星轴6,每根恒星轴上串装有两个偏心套5,两个偏心套之间相位角相差180°,使得偏心套和恒星轴连接组成曲柄机构.同时三根恒星轴上相对应位置的偏心套的相位角完全相同,通过偏心套的作用,三根恒星轴上的曲柄做完全同步的偏心旋转,共同驱动2片内齿板做平面运动,内齿板中心的内齿轮与输出外齿轮构成少齿差内啮合齿轮副,最后由与输出外齿轮相连接的齿轮轴输出运动.
|
| 图 1 减速器结构图 Figure 1 Structure of reducer 1.输入行星轮系;2.固定板;3.内齿板;4.轴承;5.偏心套;6.输入恒星轴;7.输出齿轮轴 |
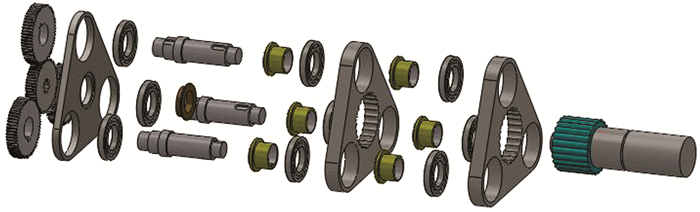
本新型小模数少齿差行星轮减速器采用恒星齿轮族集中驱动、多轴均载分流形式,大大提高了容许载荷.三偏心轴共同驱动内齿板大大提高内齿板的稳定性和少齿差齿轮副的啮合精度.其具体三维结构爆炸图如图 2所示.
|
| 图 2 爆炸图 Figure 2 Exploded view |
本文研究的对象为齿差数为1的少齿差啮合.在少齿差行星轮系传动中,由于齿差数比较小,容易产生齿廓重叠干涉等问题,为消除齿廓重叠干涉,内齿轮采用正变位齿轮,外齿轮采用负变位齿轮,齿轮压力角仍为20°.其内齿轮和外齿轮各参数如表 1所示.
| 内齿轮 | 外齿轮 | |
| 模数 | 1 | 1 |
| 齿数 | 30 | 29 |
| 压力角/(°) | 20 | 20 |
| 齿轮啮合角/(°) | 51.21 | 51.21 |
| 齿顶高系数 | 0.7 | 0.7 |
| 变位系数 | 0.331 3 | -0.127 9 |
| 齿顶圆直径/mm | 27.94 | 30.15 |
| 分度圆直径/mm | 30 | 29 |
根据转臂固定法[8],可求得少齿差传动的传动比为
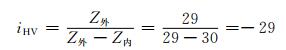 (1)
(1)
从式(1)可看出,输入与输出的运动方向相反.
运用SolidWorks对减速器各零部件按实际尺寸进行三维建模,在SolidWorks中对其进行装配,如图 3所示.

|
| 图 3 三维装配图及实物图 Figure 3 Three-dimensional assemblage diagram and practicality |
在ADAMS中进行运动学分析主要是研究零自由度系统中部件运动的位置、速度、加速度,考虑刚体系统具有确定的运动,使其自由度为零.为系统施加等于自由度的驱动约束,在一般情况下,驱动约束是系统广义坐标和时间的函数.驱动约束在其集合内部及其与运动学约束集合中必须是独立和相容的,在这种条件下,驱动系统运动学上是确定的,将作确定运动.因此只需要求解系统的约束方程:
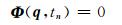 (2)
(2)
任意时刻tn位置,可由约束方程的Newton-Raphson迭代法求得:
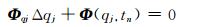 (3)
(3)
其中:Δqj=qj+1-qj,表示第j次迭代,其中q为所有铰链的拉格朗日坐标矩阵.
tn时刻速度、加速度利用线性代数方程的数值方法求解,根据CALAHAN线性代数方程[9]求解方法:
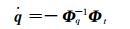 (4)
(4)
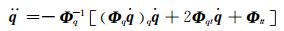 (5)
(5)
ADAMS动力学分析前会自动进行初始条件分析,利用刚体的质心笛卡尔坐标和反映刚体方位的欧拉角作为广义坐标,即:
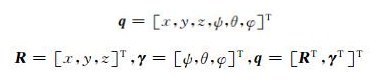 (6)
(6)
根据拉格朗日第一类方程的能量形式,ADAMS可为系统自动建立动力学方程——微分-代数方程:
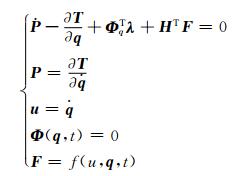 (7)
(7)
式中:P为系统的广义动量;H为外力的主表转换矩阵;T为系统广义坐标表达的动能;Φ为约束方程;F为外力矢量;λ为拉格朗日乘子向量.
对微分-代数方程的求解,ADAMS提供两种求解方式,第一种是直接降阶微分方程求解,第二种是引入约束方程将DAE方程化简为ODE方程求解.
3.2 三维模型导入及约束副的添加 3.2.1 模型导入设置在SolidWorks中建立好装配图之后,保存为*.xt格式导入ADAMS中.此时的模型是没有任何信息的.为了后面模拟仿真的准确性,必须先定义重力、材料的质量信息等,系统会自动计算质量、转动惯量、质心等并建立质心坐标系.重要零部件主要由45钢和40Cr制造,其基本属性如表 2.
| 材料 | 密度/(kg·m-3) | 模量/Pa | 泊松比 |
| 40Cr | 7.82×103 | 2.06×1011 | 0.277 |
| 45钢 | 7.85×103 | 2.11×1011 | 0.310 |
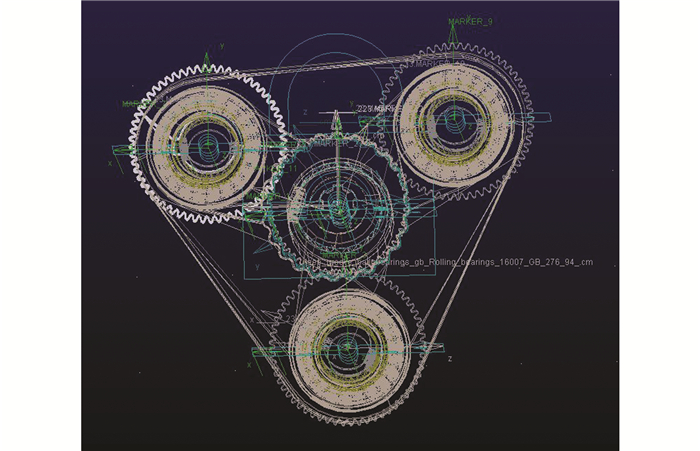
如图 4,根据实际情况,为方便模型的导入和仿真,简化三维模型里面的轴承和套筒模块为一体,分析定义各部件之间的约束关系和运动副.固定板与大地之间为固定副保证整机固定,三根恒星轴相对大地绕自己的中心旋转,设为旋转副,内齿板与外齿轮之间为便于接触力曲线的测量设置为接触副,轴承绕偏心套筒中心旋转为旋转副.输出齿轮轴相对大地有旋转运动,设置为旋转副;内齿板除了与外齿轮啮合外,自身还绕着偏心中心轴有一个公转运动,设置为旋转副.约束副添加完毕后,给三根恒星轴分别添加旋转驱动.
|
| 图 4 约束添加图 Figure 4 Adding constraint |
在ADAMS软件中,计算接触力的方法分为补偿法(Restitution)和冲击函数法(Impact).根据实际情况,本文选择冲击函数来计算齿轮啮合间的接触力,根据Impact函数来计算两个构件之间的接触力.冲击函数的基本模型如下[10]:
当q≤q1时:
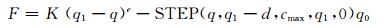
当q≥q1时:
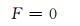
式中:STEP为阶跃函数;K为刚度系数;q1为位移量;q为碰撞过程中的变形量;cmax为接触阻尼,取为1;e为碰撞指数;q0为穿透速度.
根据内齿轮和外齿轮的材料,参考文献[11]计算出刚度系数K,其计算公式如下:
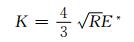 (8)
(8)
根据表 2的材料参数,计算出K=2.1×105 N/mm2/3,碰撞指数e取0.5,动摩擦系数取0.05,静摩擦系数取0.08.
添加完约束后为减速器添加驱动.根据实际情况,防止减速器转速出现突变,利用STEP函数为减速器添加转速[12], 让输入轴转速在0到0.3 s内由0增加到665 r/min,即STEP(time, 0, 0, 0.3, 3 990d·time).同时为了更好地模拟实际情况,输出轴负载也采用STEP函数,添加一个26 N·m的负载扭矩,即STEP(time, 0, 0, 0.3, 26 000).至此减速机的虚拟样机模型建成.
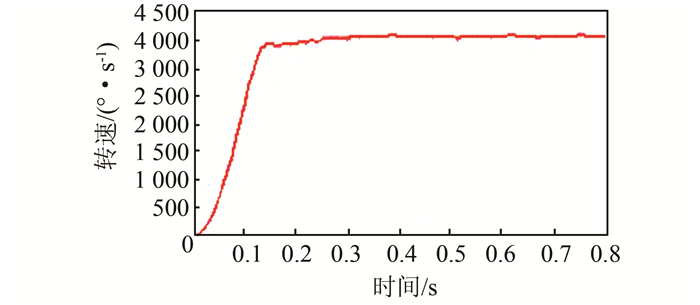
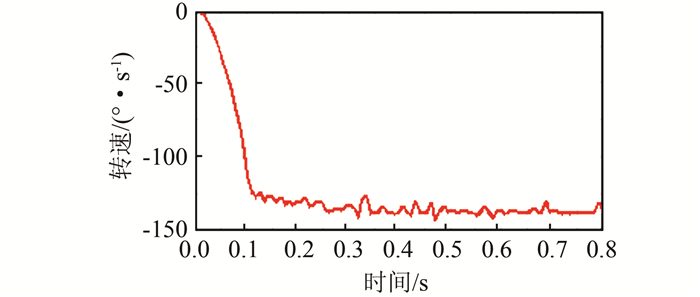
4 ADAMS后处理及仿真结果分析 4.1 仿真结果分析图 5为输入转速图.从图 5可得转速在0到0.3 s之内迅速上升,0.3 s之后达到STEP阶跃函数设定的转速665 r/min(3 990°/s),然后维持在3 990°/s附近上下波动.通过测量可得0.3 s稳定后输入转速最高峰值为4 013°/s,最低峰值为3 980°/s,平均值为3 986.5°/s,基本符合设定的输入值.图 6为输出轴的转速曲线图.把输入转速方向设定为正方向,根据少齿差传动减速比的计算方法发现输出轴的转速方向为负值反向.由图 6可看出,在短暂的响应时间后输出轴转速在0.1 s内迅速上升,在0.3 s后趋于平稳,经测量其平均值为133.68°/s,最低峰值为126.32°/s,最高峰值为141.54°/s.由于其他外力的周期性干扰作用,其输出转速存在一定的波动.可求得实际传动比i=3 986.5/133.68=29.8.其实际传动比与理论传动比基本吻合,说明了虚拟样机仿真的正确性.
|
| 图 5 输入转速曲线图 Figure 5 Input speed curve |
|
| 图 6 输出转速曲线图 Figure 6 Output speed curve |
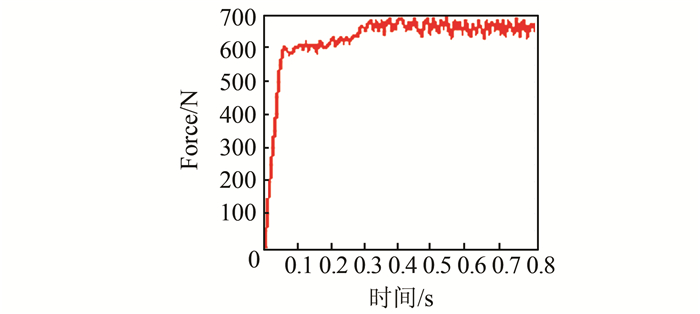
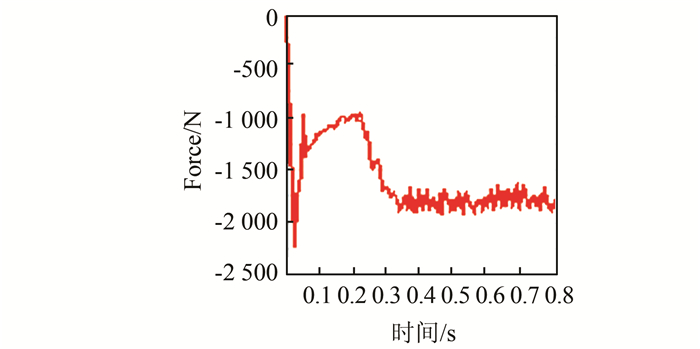
图 7和图 8分别为齿轮对啮合时X方向(径向力方向)和Y方向(圆周力方向)受力随时间变化情况.由图 7可见,随着少齿差减速器的启动,齿轮啮合对的径向力迅速增加,到0.3 s后随着输入转速稳定,其径向力也稳定下来.由于齿轮啮合时,参与啮合轮齿对数的变化,其径向力在稳定后会在一定平均值上下波动.经测量,0.3 s稳定后径向力的均值为671.51 N,最高峰值为682.32 N,最低峰值为640.87 N.因为存在周期性的外力的作用,在0.3 s后,其径向力在均值附近上下波动.如图 8所示,随着少齿差减速器的启动,圆周力方向受到一个启动冲击响应,圆周力迅速增加到2 240.32 N,随后又迅速掉落,然后在0.3 s后随着转速的稳定而趋于稳定.在0.3 s稳定后其在均值1 750.56 N附近上下波动,最高峰值为1 895.24 N,最低峰值为1 650.68 N.
|
| 图 7 X方向(径向力)受力情况 Figure 7 The force of X axis (radial force) |
|
| 图 8 Y方向(圆周力)受力情况 Figure 8 The force of Y axis (peripheral force) |
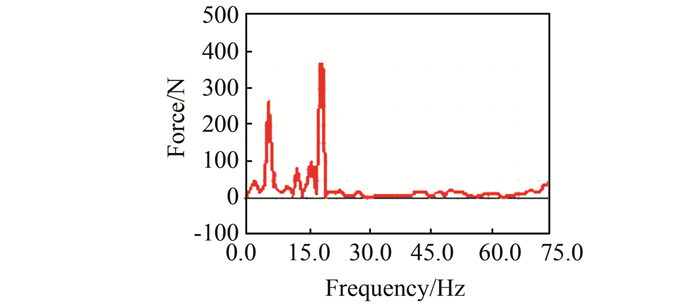
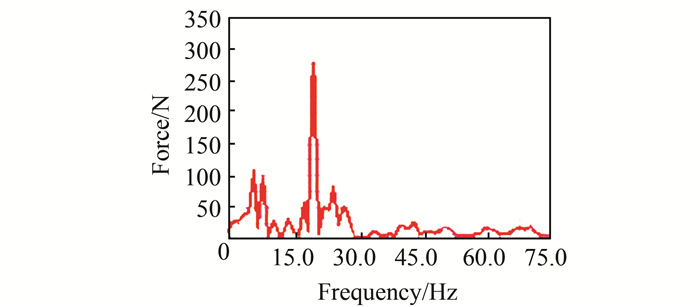
图 9和图 10分别为X和Y方向啮合力频域图.对X和Y方向受力的时域信号进行FFT傅里叶变化得到X和Y方向受力的频域图.由图可得,在频率为19 Hz附近时X和Y方向的啮合力都达到最大幅值.因此少齿差传动的啮合频率为19 Hz.根据齿轮啮合频率计算公式[13],计算得到理论值与仿真值基本吻合,再次验证了仿真的正确性.通过对频域图的分析可得此小模数少齿差减速器的啮合频率,为实际设计生产时需要避开的共振频率范围提供了理论指导.
|
| 图 9 X方向受力频域图 Figure 9 Frequency domain curve of X axis |
|
| 图 10 Y方向受力频域图 Figure 10 Frequency domain curve of Y axis |
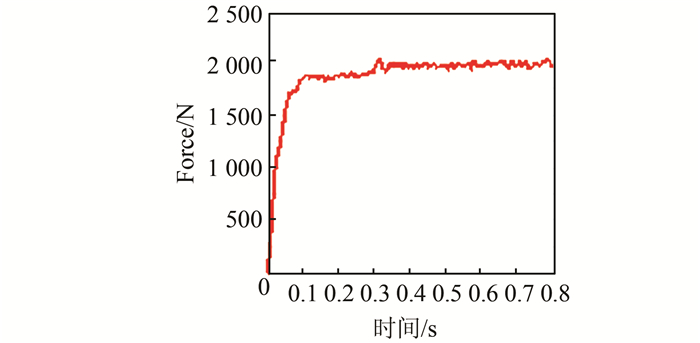
图 11为齿轮接触的法向啮合力曲线图.在ADAMS曲线后处理模块里,选择接触(contact1)的力选项,选择空间Mag曲线得到如图 11所示的曲线.其法向接触力在0.3 s内迅速增加,到0.3 s后稳定在1 950.83 N附近上下波动.其法向接触力趋势符合减速器的基本运行状况.
|
| 图 11 法向啮合力曲线图 Figure 11 The curve of normal meshing force |
由上文可知输入转速为665 r/min(3 990°/s),其减速比i=29,因此输出转速为
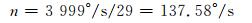 (9)
(9)
由文献[13]可计算齿轮啮合径向力、圆周力及法向力的理论值,理论值与仿真值结果如表 3所示.
| 输出转速/(°·s-1) | 径向力/N | 圆周力/N | 法向力/N | 啮合频率/Hz | |
| 理论值 | 137.58 | 652.60 | 1 793.10 | 1 908.20 | 20.13 |
| 仿真值 | 133.68 | 671.51 | 1 750.56 | 1 950.83 | 19.00 |
从表 3可看出,仿真结果与理论结果基本吻合,验证了仿真的准确性.
5 结论通过分析一种自行研发的新型行星减速器的基本结构和工作原理,将理论与实验相结合对其运动学和动力学特性进行了研究,并得出如下结论.
1) 通过仿真得到减速器的输入与输出转速,发现其与理论设计转速基本符合,能够满足实际生产需求,说明设计的合理性.同时得到齿轮啮合时接触力在X和Y方向上的时域和频域变化曲线,揭示了小模数少齿差行星减速器在工作时少齿差齿轮传动机构的受力特性和运动规律.
2) 通过接触力分析和啮合频率的分析,为以后批量生产此新型少齿差减速器选材提供一定指导,以便材料能够满足一定强度需求,避开啮合频率,防止振动.
3) 通过模拟其实际工作情况,并对其原型机进行实测,比较仿真值和实验值发现仿真结果与理论结果基本吻合.该新型少齿差行星轮减速器能够满足生产需要且具备传动平稳、响应迅速等优点,为以后进一步对小模数少齿差行星减速器的优化设计提供了理论基础.
| [1] |
朱景梓. 齿数差Z=1的渐开线K-H-V型行星齿轮减速器及其设计[J].
太原工学院学报, 1963(4): 13–42.
Zhu Jingzi. Involute K-H-V planetary gear reducer and its design of the differential gear Z=1[J]. Journal of Taiyuan Institute of Technology, 1963(4): 13–42. |
| [2] |
刘丹. 小模数渐开线少齿差减速器的设计及其传动特性研究[D]. 哈尔滨: 哈尔滨工业大学, 2012.
Liu Dan. Design of fine-pitch involute gear reducer with small tooth difference and reseach on its transmission characteristics[D]. Harbin: Harbin Institute of Technology, 2012. |
| [3] |
郑红梅, 付彬, 史越. N型少齿差行星减速器动力学仿真研究[J].
机械传动, 2013, 37(11): 89–93.
Zheng Hongmei, Fu Bin, Shi Yue. Dynamics simulation research of planetary reduction gear with small tooth deference[J]. Journal of Mechanical Transmission, 2013, 37(11): 89–93. |
| [4] |
罗庆生, 韩宝玲, 潘春荣. 精密小模数少齿差齿轮齿形的设计与加工[J].
机械传动, 2000, 24(4): 35–37.
Luo Qingsheng, Han Baoling, Pan Chunrong. The design and manufacture of the precise gear with small module and small tooth number[J]. Journal of Mechanical Transmission, 2000, 24(4): 35–37. |
| [5] |
于波, 王家序, 黄春美, 等. 基于ADAMS的孔销式少齿差行星减速器的设计与仿真分析[J].
机械设计与研究, 2013, 29(3): 23–27.
Yu Bo, Wang Jiaxu, Huang Chunmei, et al. The design and simulation analysis of hole-pin type few teeth difference lanet-gaer speed reducer based on ADAMS[J]. Journal of Machine Design and Research, 2013, 29(3): 23–27. |
| [6] |
刘丹, 唐德威, 邓忠全, 等. 少齿差齿轮传动承载能力分析及体积优化[J].
机械设计与制造, 2012(12): 39–41.
Liu Dan, Tang Dewei, Deng Zhongquan, et al. An analysis of load-bear capacity of gearing with small teeth number difference and volume optimization[J]. Machinery Design and Manufacture, 2012(12): 39–41. DOI:10.3969/j.issn.1001-3997.2012.12.014 |
| [7] |
孙恒.
机械原理[M]. 北京: 高等教育出版社, 2006: 214-299.
Sun Heng. Theory of Machines and Mechanisms[M]. Beijing: Higher Education Press, 2006: 214-299. |
| [8] |
陈华峰.
ADAMS2012虚拟样机技术从入门到精通[M]. 北京: 清华大学出版社, 2013: 14-23.
Cheng Huafeng. ADAMS 2012 Virtual Prototyping Technology from Entry to the Master[M]. Beijing: Tsinghua University Press, 2013: 14-23. |
| [9] |
郭会珍, 谭长均, 陈俊峰. 基于ADAMS的行星轮系动力学仿真[J].
机械传动, 2013, 37(5): 86–89.
Guo Huizhen, Tang Changjun, Chen Junfeng. Dynamics simulation of planetary gear train based on ADAMS[J]. Journal of Mechanical Transmission, 2013, 37(5): 86–89. |
| [10] |
龙凯, 程颖. 齿轮啮合力仿真计算的参数选取研究[J].
计算机仿真, 2002, 19(6): 87–88.
Long Kai, Chen Ying. The research of parameters by the simulation of exciting force in gears[J]. Computer Simulation, 2002, 19(6): 87–88. |
| [11] |
高广娣.
典型机械机构ADAMS仿真应用[M]. 北京: 电子工业出版社, 2013: 102-106.
Gao Guangdi. Simulation Application of ADAMS in Typical Mechanica Mechanism[M]. Beijing: Electronics Industry Press, 2013: 102-106. |
| [12] | Kahraman K. Planetary gear train dynamics[J]. Jourmal of Mechanical Design, 1994, 116(9): 712–720. |
| [13] |
濮良贵, 纪名刚.
机械设计[M]. 北京: 高等教育出版社, 2006: 198-199.
Pu Lianggui, Ji Minggang. Design of Machinery[M]. Beijing: Higher Education Press, 2006: 198-199. |
 2017, Vol. 50
2017, Vol. 50




