文章信息
- 梁佳琦, 方彦军
- LIANG Jiaqi, FANG Yanjun
- 微网下双馈风力发电系统并网运行研究
- Study of grid-connected operation of doubly-fed induction generator system under microgrid
- 武汉大学学报(工学版), 2018, 51(2): 172-177
- Engineering Journal of Wuhan University, 2018, 51(2): 172-177
- http://dx.doi.org/10.14188/j.1671-8844.2018-02-012
-
文章历史
- 收稿日期: 2016-08-15
近年来微电网中双馈风力发电系统并网运行研究普遍受到学术界与电力系统应用的关注.在我国现有的供电模式下,充分利用风能等可再生能源配合公共大电网的运行模式将促进电力系统的节能减排、加快两型社会的建设.相对传统电力系统而言,以双馈风力发电系统并入交流微电网运行具有优越性与复杂性:整个交流微电网系统不设调度,实现自身匹配,微电网中分布式电源种类繁多,运行状态多样,输出特性及控制方法各异,不确定性因素作用显著[1].因此,基于双馈风力发电系统并入交流微电网运行特点与可靠性评估分析理论,提出运行与控制策略统一、高效的并网优化算法策略对微电网系统的经济、可持续发展具有重要意义.
文献[2]针对电网电压不平衡提出双PI电流调节器控制方式,以实现在电网电压稳定不平衡的条件下双馈风力发电机运行的有效控制,计算正、负序电量分离所需时延是新问题,严重影响动态特性.文献[3-8]针对电网电压不平衡条件下采用改进的矢量控制策略时,能有选择地消除DFIG输出有功、无功功率,实现多种优化控制目标,但实施过程比较复杂,随机条件下运行对DFIG参数依赖性较大,较差的鲁棒性是新问题.文献[2-8]未对随机条件下的并网控制策略及可靠性分析做出研究.
本文提出一种新的定子磁链定向方式,基于旋转坐标系双馈异步发电机(DFIG)数学模型,进一步推导出空载、负载并网控制与DFIG矢量控制策略,并通过可行性分析来验证该方案的可靠性,以Matlab/Simulink为仿真平台,分析风力发电机在负载、空载及随机条件下对分布式电源电压、线路电压、电流、有功功率、随机风速下的风能利用系数,并通过算例进行比较,证明该方法具有可行性,为今后的风力发电并网提供了很好的理论基础.
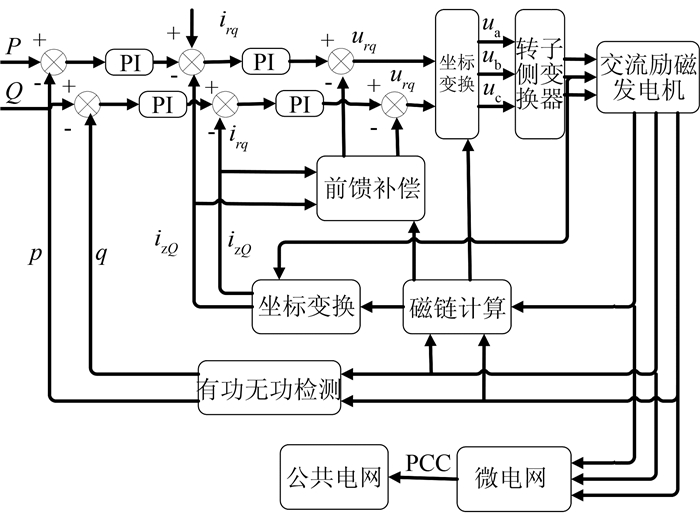
1 双馈风力发电机模型的建立与推导通过建立定子有功分量及无功分量等众多物理量之间的相互联系,可以推导出系列的矢量控制方程进行建模,更好地完善微双馈风力发电系统并入交流微电网矢量控制框图.如图 1所示[9].
|
| 图 1 双馈风力发电系统并入交流微电网矢量控制框图 Figure 1 Vector control block diagram of doubly fed wind power generation system incorporated into AC microgrid |
三相坐标系下的交流励磁发电机的数学模型是一个非线性、时变、多变量、强耦合的系统集.坐标变化法可以优化模型、降低耦合;交流励磁发电机的数学模型为
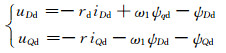 (1)
(1)
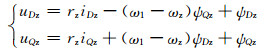 (2)
(2)
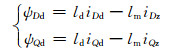 (3)
(3)
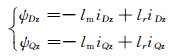 (4)
(4)
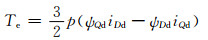 (5)
(5)
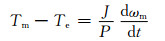 (6)
(6)
式(1)~(6)中:u、i、ψ、Tm、Te分别为电压、电流、磁链、机械转矩、电磁转矩;r、l分别为电阻、电感;ωd为定子同步电角速度;ωz为转子电角速度;ωm为发电机机械角速度;p为电机的极对数;下标D、Q分别表示d、q轴分量;下标d、z分别表示的是定子、转子分量;下标m表示定转子之间的相互作用.
将同步旋转坐标系的d轴定向在定子磁链可实现较好的控制性能,因此令rd=0可使得定子电压与定子磁链相位差相差,可求得下列关系式:
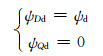 (7)
(7)
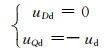 (8)
(8)
式(7)、(8)及式(2)中令rd=0,可求得下列关系式:
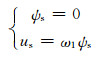 (9)
(9)
以所得电压、电流、磁链、机械转矩、电磁转矩方程式为基础进一步推出定子磁链定向空载并网控制策略.
2 定子磁链定向空载并网控制策略并网控制是对并网之前的交流励磁发电机的输出电压进行调制,使其与电网电压在幅值、频率和相位上一致,以抑制并网时的冲击电流.空载并网时,发电机空载运行,定子电流为零(没有功率输出),即iDd=iQd=0,代入方程(3)中可得:
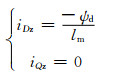 (10)
(10)
将方程式(10)分别代入(4)、(2)得:
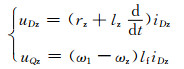 (11)
(11)
上式可作为定子磁链方向的双馈变速恒频风力发电空载并网时DFIG转子电流内环控制器的设计依据.
将式(8)代入式(4)得:
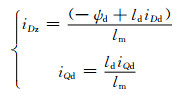 (13)
(13)
将式(13)代入式(5)得:
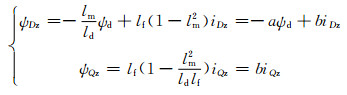 (14)
(14)
再由转子电压方程式(3)得:
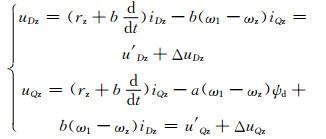 (15)
(15)
式中:u′ Dz、u′ Qz为转子电压、电流解耦控制的解耦项;ΔuDz、ΔuQz为消除转子电压、电流交叉耦合的补偿项.将转子电压分解为解耦项和补偿项后,既简化了控制,又保证了控制精度和动态响应的快速性.
其中D-Q-0同步旋转坐标下定子瞬时有功、无功功率的表达式为
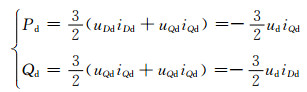 (16)
(16)
可以看出:式(16)中的发电机定子有功功率P、无功功率Q分别与定子电流的有功分量iQd、无功分量iDd成正比,通过调节iQd和iDd可以独立调节有功功率、无功功率,实现两者的独立解耦控制.
通过式(13)~(16)可以建立定子电流有功分量iQd、无功分量iDd与其他物理量之间的关系,从而实现对交流励磁发电系统的控制.
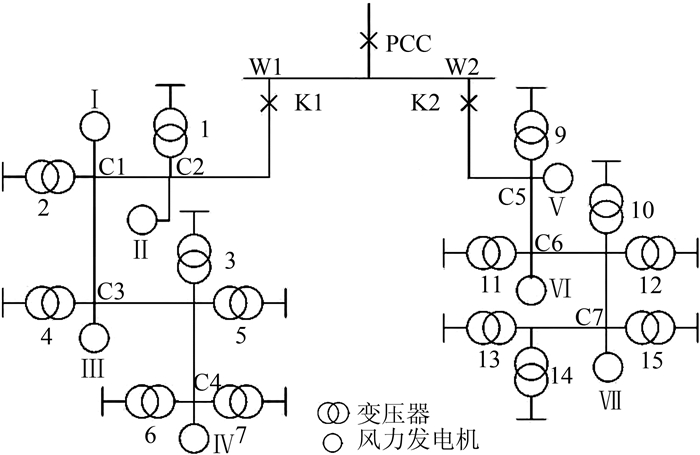
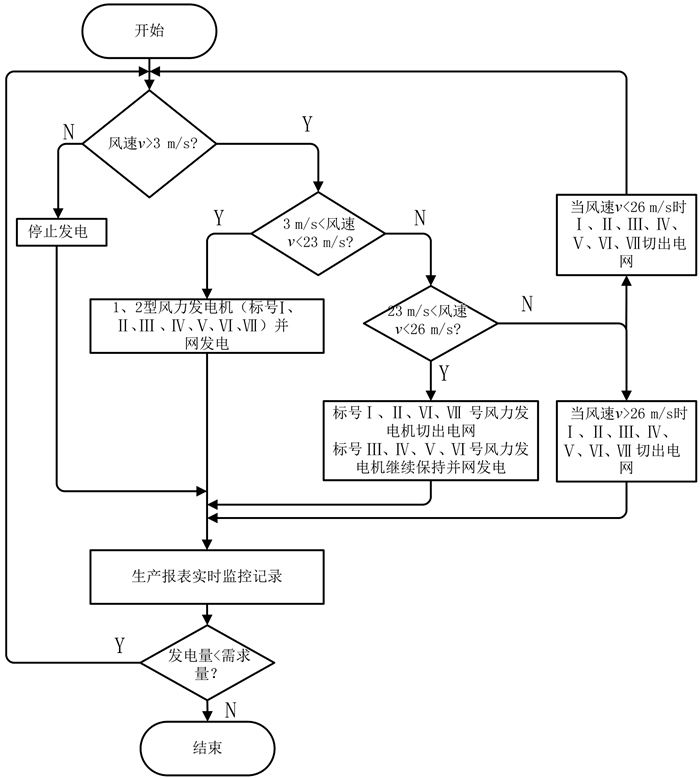
3 风力机与发电机整体框架与参数设定本文以RBTS Bus4系统为基础进行修改,馈线为以W1、W2组成的配电系统,在此基础上进一步对系统内部风力发电机进行具体仿真分析,其系统结构图如图 2所示[10-13].风速的大小是风能转化为电能的一项重要检测指标,当现场风速与风力机自身性能相比较后作出正确的发电行为可以调高发电质量,将现场风速与切入、切出风速不断比较,以调控发电机的运作可实现最大化利用,其流程图如图 3所示.
|
| 图 2 基于风力发电机的微电网并网接线 Figure 2 Based on wind turbine generator microgrid connection |
|
| 图 3 系统整体运行流程框图 Figure 3 Flowchart of whole operation |
小型微电网是由2种型号(共7台风力发电机)组成,因此有3种双馈风力发电机系统并入微网组网形式,通过开闭每条馈线首端开关K1、K2来组合并网方式.风力发电机及PCC可靠性参数如表 1~3所示.
| 参数名 | 额定功率/kW | 额定频率/Hz | 额定线电压/V | 定子绕组漏感/mH | 定子绕组电阻/Ω | 互感/mH | 转动惯量 /(kg·m2) |
极对数 | 转子绕组电阻/Ω | 转子绕组漏感/mH |
| 参数值 | 10 | 50 | 380 | 1.0 | 0.369 | 41.9 | 0.37 | 3 | 0.308 | 2.1 |
| 电源类型 | 停运率/% | 恢复时间/h |
| PCC | 11.06 | 8 |
| 风力发电机1~3 | 9.636 | 48 |
| 风力发电机类型 | 接入发电机标号 | 额定功率/MW | 切入风速/(m·s-1) | 额定风速/(m·s-1) | 切出风速/(m·s-1) |
| 1 | Ⅰ、Ⅱ、Ⅵ、Ⅶ | 1.5 | 3 | 12 | 23 |
| 2 | Ⅲ、Ⅳ、Ⅴ、Ⅵ | 1.2 | 3 | 14.3 | 26 |
如图 2所示,将开关K1、K2闭合,模拟一天当中发电量达到最大值时,双馈风力发电系统并入交流微电网运行仿真监测,分析如下所述.
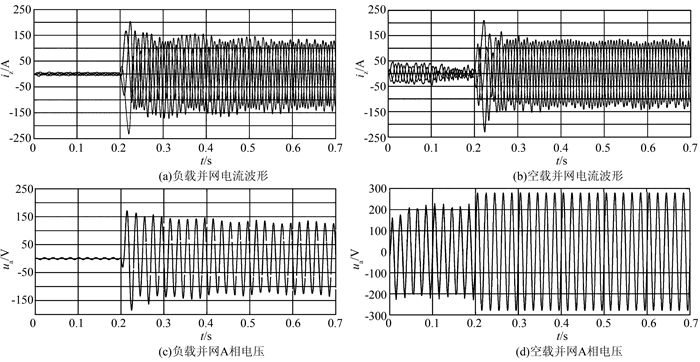
4.1 负载、空载并网运行条件下转子电流、电压波形图 4(a)、(c)与(b)、(d)分别表示负载并网运行下转子三相电流波形图、A相电压波形图与空载并网运行下转子三相电流波形图与A相电压波形图.在负载并网与空载并网下转子电流、电压在0~0.2 s时间内做并网调节,0.2 s后达到稳定状态.表明在发电初始阶段, DFIG对末端电能质量不断进行反馈检测, 符合前述并网控制策略.由此可见,负载、空载并网过程中转子电流无较大冲击,过渡平稳,响应时间快,满足并网条件.
|
| 图 4 并网运行下转子电流波形 Figure 4 Rotor current waveform under grid connected operation |
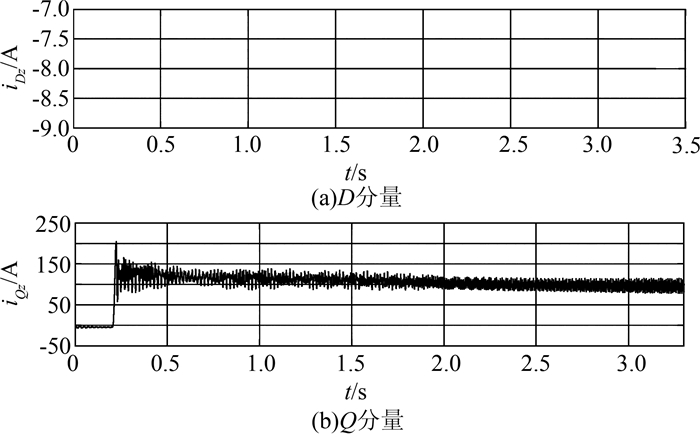
由图 5可知,有功分量iQz发生变化,但iDz未发生变化,说明有功功率可以独立调节,从而得到最优化并网控制.
|
| 图 5 转子侧电流在DQ分量上的变化仿真波形 Figure 5 Simulation waveforms of rotor side current variation on DQ component |
图 6为定侧A相电压图ua和电流图ia,将电压放大20倍,电压、电流频率恒定,相位相反,表明定子侧正在工作并向电网发出电功率.
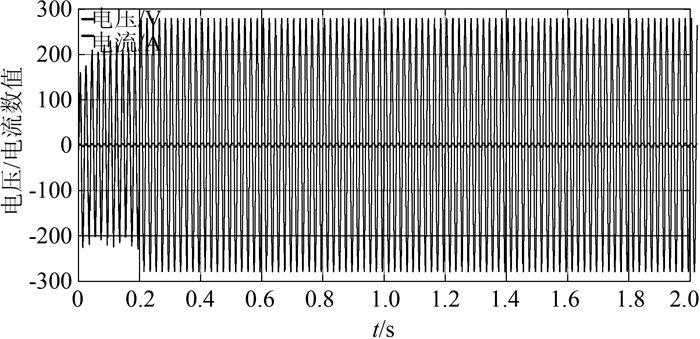
|
| 图 6 定子侧A相电压波形图与电流仿真波形图 Figure 6 Simulation of stator side A-phase current and voltage waveform |
图 7表示并网后风速在2 s时刻由6 m/s变为10 m/s,在4 s时刻由10 m/s变为15 m/s,初始仿真无功功率恒为20 Var.由仿真得出随机风速下随着风速的变化有功功率P相应改变,无功功率Q保持不变,充分表明发电效率高,损耗低.
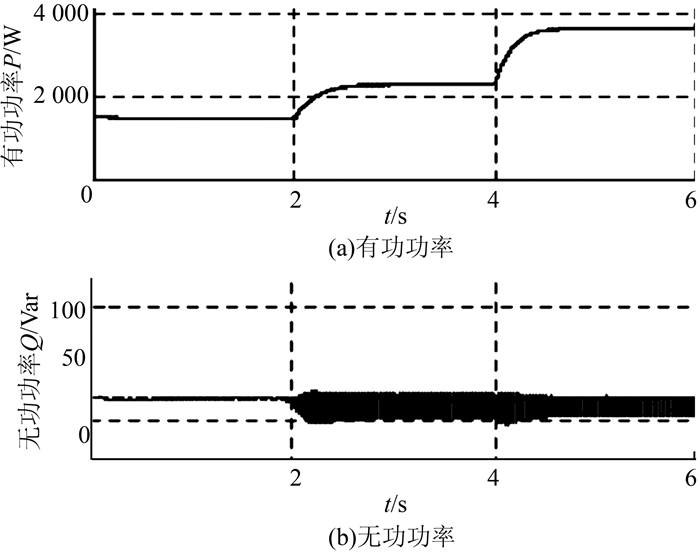
|
| 图 7 功率调节仿真 Figure 7 The simulation curves of adjusting power |
图 8为风能利用系数变化曲线,风能利用系数保持在较高的数值0.480附近,说明在随机风速的变化过程中,机组能够按最大风能捕获的机理运行.
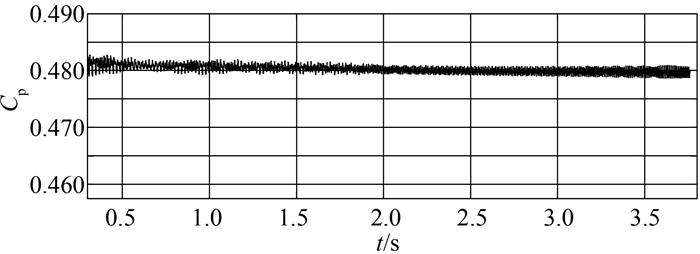
|
| 图 8 随机风速仿真 Figure 8 The stochastic wind speed simulation |
以本文第2部分的模型作为参考,利用蒙特卡洛算法对微电网的3种组合方式的运行模式、负荷等进行可靠性评估,结果显示该方案可行性较高,可根据负荷用电量自行决定微网组成,其并网电能质量较高.可行性评估报告如表 4所示.
| 微电网组成 | 微网总负荷/MW | 总容量 /负荷 |
可靠性 | |||||
| 非微网模式 | 含风力发电机并网运行模式 | 含风力发电机孤岛运行模式 | ||||||
| 解析算法 | 蒙特卡洛算法 | 解析算法 | 蒙特卡洛算法 | |||||
| W1 | 3.61 | 1.538 | 0.99 | 0.995 8 | 0.995 3 | 0.576 | 0.538 | |
| W2 | 3.58 | 1.032 | 0.99 | 0.991 9 | 0.991 6 | 0.199 | 0.156 | |
| W1+W2 | 7.19 | 1.206 | 0.99 | 0.993 3 | 0.993 8 | 0.352 4 | 0.324 | |
本文针对交流励磁风力发电机并入微电网冲击较大及功率控制不佳的现状分别建立了定子磁链定向模型,推导出空载、负载并网控制与DFIG矢量控制策略,结合可靠性评估验证了该方案的有效性.该方案具有以下优点:
1) 针对现场的不同风速,微电网可根据负荷需要及风力发电机自身性能采取不同组合并网,具有能源最大化利用及设备最大化保护优势.
2) 在随机风速(介于切入、切出风速之间)、负载变化环境下可实现自我快速、优质调节,满足恒频、恒压等众多高性能指标需要.
3) 本模型的应用具有不设调度、自身匹配、自动调节及主动配电等优势,高质量满足微电网并网条件,为以后微电网大规模并网及小区域高质量自配供电奠定了一定的理论基础.
| [1] | Ma Yiwei, Yang Ping, Wang Yuewu, et al. Typical characteristics and key technologies of microgrid[J]. Automation of Electric Power Systems, 2015, 39(8): 168–175. |
| [2] | Xu L, Wang Y. Dynamic modeling and control of DFIG-based wind turbines under unbalanced network conditions[J]. IEEE Transactions on Power Systems, 2007, 22(1): 314–323. DOI:10.1109/TPWRS.2006.889113 |
| [3] | Banakar H, Luo C, Ooi B T. Steady-state stability analysis of doubly-fed induction generators under decoupled P-Q control[C]// IEEE Proceedings online no. 20050388, 300-306. |
| [4] | Lopez J, Gubia E, Sanchis P, et al. Wind turbines based on doubly fed induction generator under asymmetrical voltage dips[J]. IEEE Transactions on Energy Conversion, 2008, 23(1): 321–330. DOI:10.1109/TEC.2007.914317 |
| [5] | Xu L, Wang Y. Dynamic modeling and control of DFIG-based wind turbines under unbalanced network conditions[J]. IEEE Transactions on Power Systems, 2007, 22(1): 314–323. DOI:10.1109/TPWRS.2006.889113 |
| [6] | Hu J, He Y, Wang H. Adaptive rotor current control for wind-turbine driven DFIG using resonant controllers in a rotor rotating reference frame[J]. Journal of Zhejiang University-Science A, 2008, 9(2): 149–155. DOI:10.1631/jzus.A073026 |
| [7] | Hu J, He Y. Modeling and enhanced control of DFIG under unbalanced grid voltage conditions[J]. Electric Power Systems Research(EPSR), 2009, 79(2): 273–281. DOI:10.1016/j.epsr.2008.06.017 |
| [8] | Xu L. Coordinated control of DFIG's rotor and grid side converters during network unbalance[J]. IEEE Transactions on Power Electronics, 2008, 23(3): 1041–1049. DOI:10.1109/TPEL.2008.921157 |
| [9] | Tong Dawei. Research on the switching control strategy of microgrid islanded and grid-connected modes[D]. Harbin: Harbin Institute of Technology, 2014. |
| [10] | Allan R N, Billinton R, Sjarief I, et al. A reliability test system for educational purposes-basic distribution system data and results[J]. IEEE Transactions on Power Systems, 1991, 6(2): 813–820. DOI:10.1109/59.76730 |
| [11] | Jaehong Kim, Josep M. Guerrero, Pedro Rodriguez. Mode adaptive droop control with virtual output impedances for an inverter-based flexible AC microgrid[J]. IEEE Power Electronics Society, 2011, 26(3): 689–701. DOI:10.1109/TPEL.2010.2091685 |
| [12] | Joan Rocabert, Alvaro Luna, Frede Blaabjerg. Control of power converters in AC microgrids[J]. IEEE Transactions on Power Electronics, 2012, 27(11): 4734–4749. DOI:10.1109/TPEL.2012.2199334 |
| [13] | Navid Eghtedarpour, Ebrahim Farjah. Power control and management in a hybrid AC/DC microgrid[J]. IEEE Transactions on Smart Grid, 2014, 5(3): 1494–1505. DOI:10.1109/TSG.2013.2294275 |
 2018, Vol. 51
2018, Vol. 51




