文章信息
- 李志伟, 叶曦, 乐健, 刘开培
- LI Zhiwei, YE Xi, LE Jian, LIU Kaipei
- 基于混合整数规划的虚拟发电厂经济最优化出力研究
- Optimal dispatch strategy of virtual power plant based on mixed-integer programming
- 武汉大学学报(工学版), 2018, 51(12): 1093-1097
- Engineering Journal of Wuhan University, 2018, 51(12): 1093-1097
- http://dx.doi.org/10.14188/j.1671-8844.2018-12-008
-
文章历史
- 收稿日期: 2017-11-12
近年来,随着风电、太阳能发电和储能设备等大规模新能源在电力系统中的大量渗透,传统的电力系统结构、形态与运行控制方式随之产生根本性变革,加之智能电网技术的快速发展与成熟,虚拟发电厂的概念与相关研究逐渐为国内外学术界重视与关注.
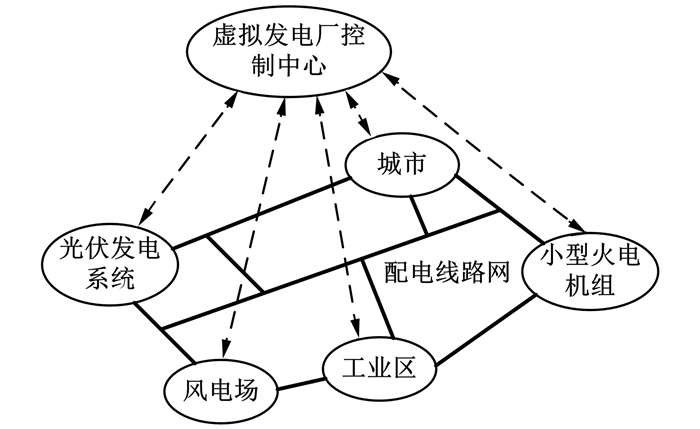
虚拟发电厂是将一定区域内的传统发电厂、分布式电源、可控负荷和储能系统有机结合,通过一个控制中心的管理和调控,合并为一个整体参与电网的运行[1],其典型结构如图 1所示.
|
| 图 1 虚拟发电厂的一种典型结构图 Fig. 1 A typical structure of VPP |
虚拟发电厂作为一个整体参与电网调控,因此其作为一个整体有必要考虑自身的经济效益,从分布式电源持有方和未来电力市场改革角度考虑经济效益最大化才是虚拟发电厂的主要目标.考虑到风能、太阳能出力不确定性等因素,有些文献也提到微电网动态经济调度问题[2],同时为了协调用户、虚拟发电厂和输配电网管理调度中心之间的经济技术问题,有学者对三方的竞价策略进行了相关研究[3, 4].
对于虚拟发电厂接入下的可控机组如小型火电机组或者燃气轮机等,可以通过控制其启停状态使得在满足一定条件时虚拟发电厂经济效益最大,这就不可避免地使得虚拟发电厂的经济优化调度模型中有很多整数决策变量,因此虚拟发电厂的最优经济调度问题实则是:在满足一定的约束条件下,以经济效益最大为目标函数的混合整数规划问题[5, 6].
论文基于LINGO优化仿真软件,结合MATLAB平台对此混合整数规划问题进行求解,以IEEE-33节点10 kV配电网系统(不考虑配电网的闭环运行)为例,建立含有风电、光电、储能设备以及传统火电机组的虚拟发电厂架构模型,基于风电光伏功率预测曲线、电力市场实时电价以及各分布式电源的一系列自身约束条件等,以虚拟发电厂经济效益最大为目标函数进行数值分析求解,得到各分布式电源的最优有功出力情况.
1 虚拟发电厂经济优化调度模型虚拟发电厂的最优化经济调度问题实则就是混合整数规划问题:以虚拟发电厂利润最大化为目标函数,一些经济和技术限制条件为约束,得到虚拟发电厂不同机组的最优调度策略.下面以IEEE-33节点10 kV配电网系统(不考虑配电网的闭环运行)为例,进行虚拟发电厂的经济优化调度算例建模.
1.1 目标函数虚拟发电厂经济优化调度模型,以虚拟发电厂的最大利润为目标函数,即虚拟发电厂下的各分布式电源在满足一定约束条件下最优有功出力所得的总收益,去掉各分布式电源本身燃料成本和运行维护成本等成本后,余下净收益的最大值,各表达式为
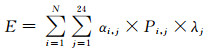 (1)
(1)
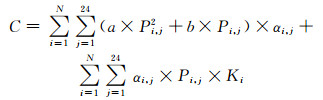 (2)
(2)
式中:E为收益;C为成本;N为分布式电源的数目;i为分布式电源的编号;j为一天的时刻;αi, j为第i个DG在j时刻的启停状态,取0或1;Pi, j为第i个DG在j时刻的有功出力;λj为j时刻的电力市场电价;Ki为第i个DG的运行维护成本系数;a为火电机组燃料成本2次项系数;b为火电机组燃料成本1次项系数.
其中,由于风能、太阳能是清洁能源,不考虑燃料成本,只考虑运行维护成本(与其有功出力成正比);本文暂不考虑储能系统的运行维护成本,且储能设备的有功出力可正可负,正代表储能设备作为电源向电网供电,负代表其将电能储存起来[7];火电机组既有燃料成本也有运行维护成本.
1.2 约束条件虚拟发电厂经济优化调度模型需要考虑的约束条件有:各分布式电源的功率上下限、功率平衡约束、爬坡功率约束、蓄电池容量约束等.
1) 各分布式电源功率上下限约束
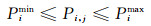 (3)
(3)
2) 功率平衡约束
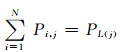 (4)
(4)
3) 爬坡功率约束
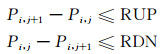 (5)
(5)
4) 蓄电池容量约束
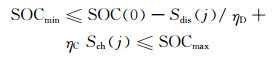 (6)
(6)
式中:Pimin为第i个DG的功率下限;Pimax为第i个DG的功率上限;PL(j)为j时刻的网络有功负荷;RUP为增负荷时的出力增加限值;RDN为减负荷时的出力减少限值;SOCmin为蓄电池的最小剩余容量;SOCmax为蓄电池的最大剩余容量;ηC为蓄电池的充电效率;ηD为蓄电池的放电效率;SOC(0)为蓄电池的初始容量;Sdis(j)为从初始时刻到t时刻的放电量;Sch(j)为从初始时刻到t时刻的放电量.
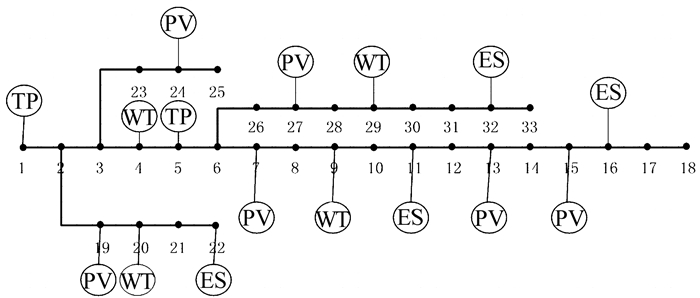
2 算例分析论文以IEEE-33节点10 kV配电网系统为例,建立含有4组风电(Wind Turbine, WT)、6组光电(Photovoltaic, PV)、4组储能设备(Energy Storage, ES)以及2组小容量火电机组(Thermal Power, TP)的虚拟发电厂架构模型进行仿真计算,网络拓扑图[8]如图 2所示.
|
| 图 2 DG接入电网的网络拓扑示意图 Fig. 2 IEEE topology diagram connected to DGs |
由优化算例的目标函数和约束条件可知,需要给出模型所需要的参数,如各DG基本参数、火电机组爬坡功率约束、电力市场实时电价、实时负荷变化等信息[9, 10],下面依次给出模型所需要的各种参数,如表 1~3所示.
| DG种类 | DG数目 | DG额定功率/kW | 出力限值/kW | 运行维护成本系数 | |
| RUP | RDN | ||||
| 风电机组 | 4 | 30 | 0.08 | ||
| 光电机组 | 6 | 15 | 0.08 | ||
| 储能设备 | 4 | 40 | 0.03 | ||
| 火电机组 | 2 | 100 | 10 | 10 | 0.05 |
| 时刻 | 电价/(元·(kW·h)-1) | 时刻 | 电价/(元·(kW·h)-1) | |
| 1 | 0.52 | 13 | 097 | |
| 2 | 0.43 | 14 | 0.82 | |
| 3 | 0.45 | 15 | 0.71 | |
| 4 | 0.48 | 16 | 0.59 | |
| 5 | 0.52 | 17 | 0.63 | |
| 6 | 0.59 | 18 | 0.61 | |
| 7 | 0.67 | 19 | 0.78 | |
| 8 | 0.76 | 20 | 0.81 | |
| 9 | 0.85 | 21 | 0.88 | |
| 10 | 0.88 | 22 | 0.77 | |
| 11 | 0.71 | 23 | 0.65 | |
| 12 | 0.92 | 24 | 0.58 |
| 时刻 | 负荷/kW | 时刻 | 负荷/kW | |
| 1 | 168 | 13 | 386 | |
| 2 | 115 | 14 | 348 | |
| 3 | 81 | 15 | 287 | |
| 4 | 60 | 16 | 230 | |
| 5 | 30 | 17 | 211 | |
| 6 | 30 | 18 | 224 | |
| 7 | 89 | 19 | 247 | |
| 8 | 121 | 20 | 265 | |
| 9 | 176 | 21 | 248 | |
| 10 | 208 | 22 | 199 | |
| 11 | 258 | 23 | 183 | |
| 12 | 321 | 24 | 174 |
表 1给出了各个分布式电源的基本参数和运行参数,其中火电机组的发电成本系数未列出,分别为:a=0.008, b=0.01.
表 2、3分别给出了日前电力市场的实时电价变化情况和配电网负荷的实时需求量,以便优化模型中目标函数最大利润的计算和约束条件中功率平衡条件的实现.
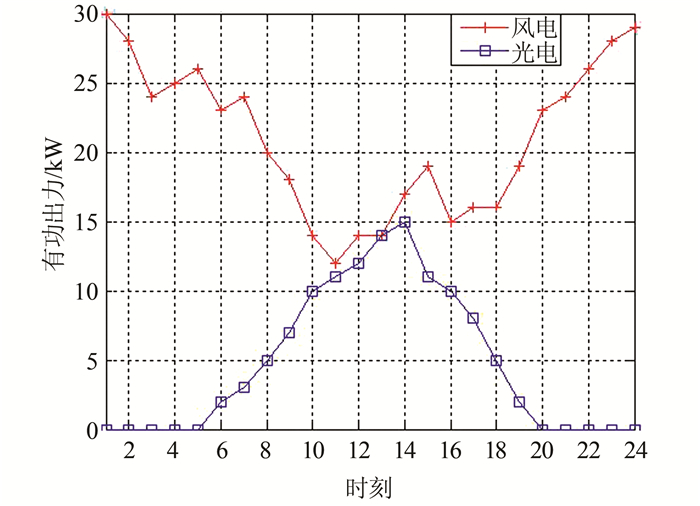
2.2 风电、光伏功率预测由于风电机组和光伏机组的出力情况受自然环境的影响,有很多干扰因素和随机情况发生,存在很多不确定性,因此在对分布式电源进行经济最优化调度时,应该考虑这种不确定性才能使得仿真结果更加准确可靠,因此需要对光伏和风电机组的出力进行相关预测,论文假设所有的风电机组和光伏机组的出力预测曲线一致.根据历史经验数据,光伏机组和风电机组的功率预测曲线如图 3所示.
|
| 图 3 风电、光伏的功率预测曲线 Fig. 3 Power prediction curve of wind turbines (WTs) and photovoltaics (PVs) |
论文基于LINGO11优化仿真软件,结合MATLAB对此混合整数规划问题进行求解,以IEEE-33节点10 kV配电网系统(不考虑配电网的闭环运行)为例,建立含有风电、光电、储能设备以及小容量火电机组的虚拟发电厂架构模型[11],基于分布式电源功率预测、电力市场实时电价和各分布式电源的一系列自身约束条件,以虚拟发电厂经济效益最大为目标函数进行数值分析求解,可以得到各分布式电源24 h的最优经济调度情况,也验证了LINGO较为完善地解决了虚拟发电厂最优化经济调度的混合整数规划问题.
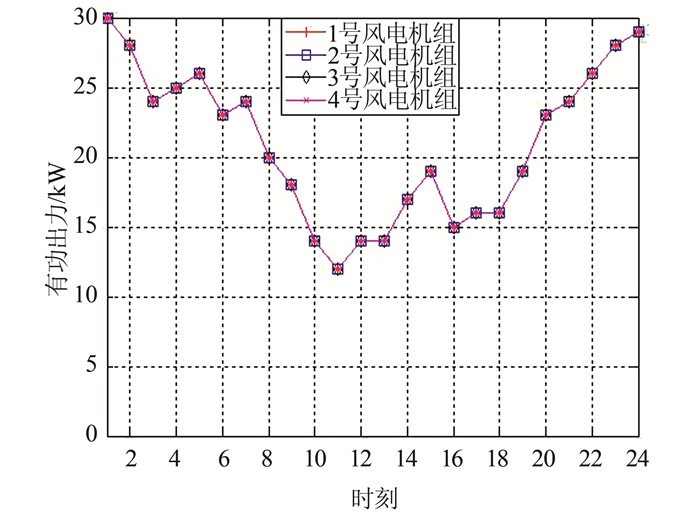
基于LINGO11优化软件对上述模型进行分析求解,经过数值仿真可以得到在虚拟发电厂经济效益最大的情况下各分布式电源的功率出力情况,如图 4~7所示.
|
| 图 4 风电机组的经济最优出力情况 Fig. 4 Optimal outputs of WTs |
|
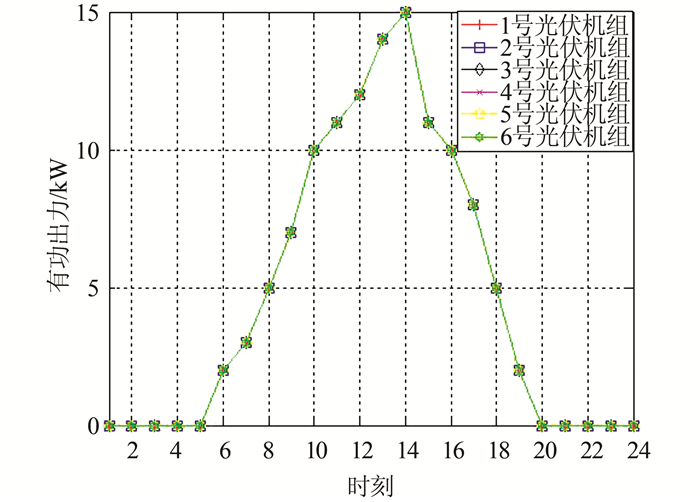
| 图 5 光伏机组的经济最优出力情况 Fig. 5 Optimal outputs of PVs |

|
| 图 6 小容量火电机组的经济最优出力情况 Fig. 6 Optimal outputs of TPs |
|
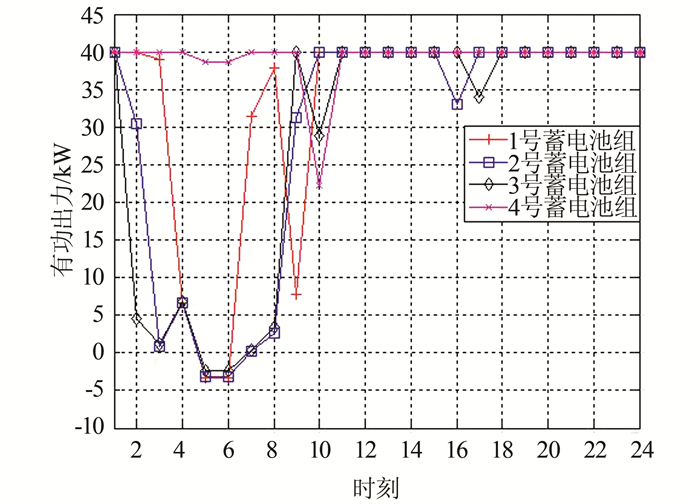
| 图 7 蓄电池组的经济最优出力情况 Fig. 7 Optimal outputs of ESs |
图 4~7中各DG出力为0代表其对应的控制决策变量为0(关停状态).
由图 4、5可知,风电机组和光伏机组大致都是按照功率预测曲线,以最大功率输出参与VPP的经济优化调度,最大限度地提高清洁能源的利用程度.
由图 6的小容量火电机组的经济最优出力情况可知,虚拟发电厂中接入的小容量火电机组在7~19时刻处于工作状态,开始向电网输送电能;实际上从表 3的负荷实时需求量可知,在7~19时刻是用电高峰期,因此需要投入火电机组进行补偿高峰期的负荷使用,火电机组处于工作状态,而当在用电低谷时需要关停一部分或全部火电机组.
由于在1~8时刻的负荷需求量偏低,储能设备只需要向电网供给很少一部分电能就可以满足功率平衡条件,同时在4~7时刻负荷需求极低,储能设备就可将电网中微量的剩余电能储存起来,这和仿真结果图 7的蓄电池组的经济最优出力情况一致.
3 结语本文以最大化商业型虚拟发电厂的利润为目标函数,考虑分布式电源自身限制条件和网络运行条件等作为约束条件,计及小型可控机组启停状态,建立了商业型虚拟发电厂经济优化调度的混合整数规划优化数学模型,基于LINGO优化仿真软件对该混合整数规划优化问题进行分析求解.给出了含风力发电、光伏发电、储能单元以及小型可控机组的虚拟发电厂仿真算例,通过仿真验证了所提出最优经济调度方法的正确性和有效性.
电力市场电价的精确分析和预测,对虚拟发电厂的实时最优经济调度起到关键作用;虚拟发电厂有时还要协调辅助输配电网进行安全运行与调度,同时要完善虚拟发电厂、用户和输配电网管理中心的三方竞价协调机制,在此基础上的虚拟发电厂经济最优调度计划将是急需解决的问题,也是笔者下一步的研究重点.
| [1] |
刘吉臻, 李明扬, 房方, 等. 虚拟发电厂研究综述[J]. 中国电机工程学报, 2014, 34(29): 5103-5111. Liu Jizhen, Li Mingyang, Fang Fang, et al. Review on virtual power plants[J]. Proceedings of the CSEE, 2014, 34(29): 5103-5111. |
| [2] |
肖青, 陈洁, 杨秀, 等. 含多种分布式电源的微网动态经济调度[J]. 电力系统及其自动化学报, 2013, 25(4): 22-28. Xiao Qing, Chen Jie, Yang Xiu, et al. Dynamic economic dispatch of microgrid with different types of distributed generations[J]. Proceedings of the CSU-EPSA, 2013, 25(4): 22-28. DOI:10.3969/j.issn.1003-8930.2013.04.005 |
| [3] |
Elaheh Mashhour, Seyed Masoud Moghaddas-Tafreshi. Bidding strategy of virtual power plant for participating in energy and spinning reserve markets-partⅠ:numerical problem formulation[J]. IEEE Transactions on Power Systems, 2011, 26(2): 949-956. DOI:10.1109/TPWRS.2010.2070884 |
| [4] |
Elaheh Mashhour, Seyed Masoud Moghaddas-Tafreshi. Bidding strategy of virtual power plant for participating in energy and spinning reserve markets-partⅡ:numerical analysis[J]. IEEE Transactions on Power Systems, 2011, 26(2): 957-964. DOI:10.1109/TPWRS.2010.2070883 |
| [5] |
Arthur Richards, Jonathan How. Mixed-integer programming for control[C]//AACC, 2005: 2676-2683.
|
| [6] |
Marko Zdrilic, Hrvoje Pandzic, Igor Kuzle. The mixed-integer linear optimization model of virtual power plant operation[C]//IEEE, 2011: 467-471.
|
| [7] |
Zheng Yu, Dong Zhaoyang, Huang Shilin. Optimal integration of mobile battery energy storage in distribution system with renewable[J]. Clean Energy, 2015, 3(4): 589-596. |
| [8] |
Neeraj Kanwar, Nikhil Gupta, Niazi K R, et al. Optimal distributed generation allocation in radical distribution systems considering customer-wise dedicated feeders and load patterns[J]. Clean Energy, 2015, 3(4): 475-484. |
| [9] |
Peikherfeh M, Seifi H, Sheikh-EI-Eslami M K. Optimal dispatch of distributed energy resources included in a virtual power plant for participating in a day-ahead market[C]//IEEE, 2011: 204-210.
|
| [10] |
Mohamad Amin Salmani, Arash Anzalchi, Soudeh Salmani. Virtual power plant: new solution for managing distributed generations in decentralized power systems[C]//IEEE, 2010: 126-131.
|
| [11] |
周晓燕, 刘天琪, 沈浩东, 等. 含多种分布式电源的微电网经济调度研究[J]. 电工电能新技术, 2013, 32(1): 5-8. Zhou Xiaoyan, Liu Tianqi, Shen Haodong, et al. Research on economic dispatch of microgrid with multi-distributed generation[J]. Advanced Technology of Electrical Engineering and Energy, 2013, 32(1): 5-8. DOI:10.3969/j.issn.1003-3076.2013.01.002 |
 2018, Vol. 51
2018, Vol. 51




