文章信息
- 赵福云, 任秀宏, 胡江涛, 张纪豪
- ZHAO Fuyun, REN Xiuhong, HU Jiangtao, ZHANG Jihao
- 太阳能烟囱通风特性及其强化
- Ventilation performance of solar chimney and its reinforcement
- 武汉大学学报(工学版), 2017, 50(5): 714-719
- Engineering Journal of Wuhan University, 2017, 50(5): 714-719
- http://dx.doi.org/10.14188/j.1671-8844.2017-05-012
-
文章历史
- 收稿日期: 2016-12-27
2. 河南科技大学土木工程学院,河南 洛阳 471023
2. School of Civil Engineering, Henan University of Science and Technology, Luoyang 471023, China
随着可持续发展战略的提出,建筑自然通风技术越来越受到人们的重视.合理利用自然通风可改善建筑热湿环境、减少空调能耗.太阳能烟囱是热压作用下强化自然通风压头和风量的一种设备,它吸收太阳辐射热并将热能转化为动能,从而为空气流动提供浮升力.至今,人们对太阳能通风系统在理论、实验和数值模拟方面进行了大量的研究工作[1-9].
流量是评价太阳能烟囱性能的一个非常重要的指标,当出口出现回流时会导致流量减小.Gan和Riffat(1998)[10]使用CFD技术研究了太阳能烟囱的性能,在非对称加热的条件下,2.8 m高吸热墙的太阳能烟囱当烟囱宽度超过0.2 m,出口处出现回流,导致流量减小,当宽度继续增大,回流深度会到达烟囱的中心处.Chen et al(2003)、Jing和Li (2012)[11, 12]通过实验验证了在烟囱出口的回流现象.Gan(2006)[13]数值模拟了6 m高的太阳能烟囱,当宽度大于0.55 m,在非对称加热的情况下该烟囱会出现回流.Khanal和Lei(2012,2014)[14, 15]提到回流是由于热边界层对下游空气的卷吸,渗透深度随着Ra的增大而增大,为了避免回流,提出一种一侧倾斜式太阳能烟囱,通过数值模拟和实验验证了新型太阳能烟囱可以有效避免回流,从而提高烟囱性能.尽管许多学者对太阳能烟囱中的回流现象通过数值模拟和实验进行了研究,但如何在不改变结构尺寸情况下有效减少回流,增大烟囱通风量还鲜有报道.
本文将离散热源置于玻璃侧内表面,并探讨其位置和高度对太阳能烟囱热表面换热强度和烟囱通风量的影响[16, 17],使其可以避免回流,提高烟囱流量.通过数值方法模拟空气在烟囱内流动过程,利用流线和热线实现流体和热量传递的可视化[18, 19],深入探讨其流动和热量传递机理,为太阳能烟囱在被动式建筑通风系统中更有效应用提供有力的理论支持.
1 物理问题描述图 1描述了太阳能烟囱的简化二维物理模型,吸热墙高度为Ha, 吸热墙和玻璃之间的宽度为Wg, 其高宽比Ar=Ha/Wg=5.图 1(a)为普通太阳能烟囱,图 1(b)为离散热源式(Discrete Heat Sources, NHS)太阳能烟囱.离散热源高度及间距用如图 1(b)所示字母表示.本文对模型做了如下假设:
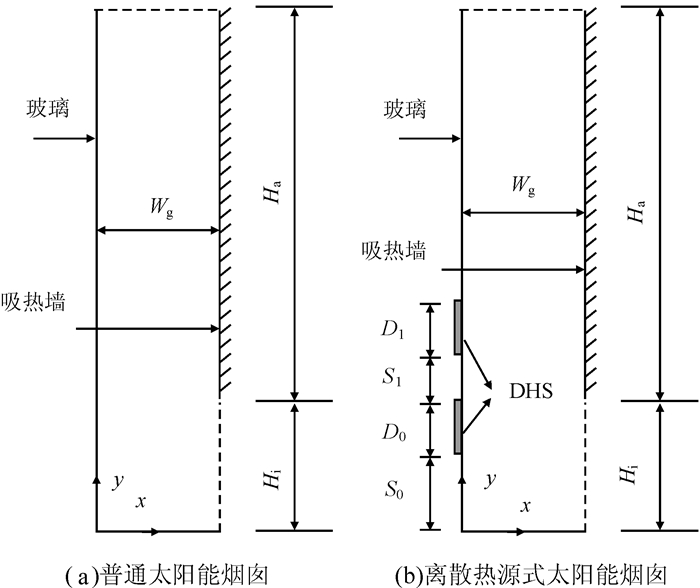
|
| 图 1 太阳能烟囱物理模型 Figure 1 Illustration of physical model for solar chimney |
1) 烟囱内空气流动为稳态、层流流动;
2) 烟囱内空气为不可压缩的牛顿流体;
3) 空气的所有物性参数均视为常数,但密度随温度的变化遵循Boussinesq假设;
4) 不考虑壁面的辐射;
5) 不考虑烟囱吸热壁面的蓄热.
1.1 控制方程空间长度尺度为Wg, 速度尺度为U0=(α/Wg)1/2, 温度尺度为Δt=(q″Wg/λ),基于上述假设和特征尺度,无因次质量、动量和能量守恒方程如下:
 (1)
(1)
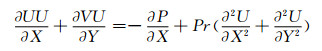 (2)
(2)
 (3)
(3)
 (4)
(4)
上述方程中无因次量与有因次量之间的关系为
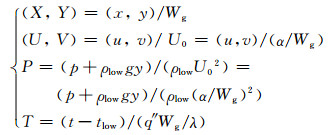 (5)
(5)
同时引入的无因次控制参数为
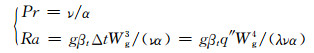 (6)
(6)
空气的Pr=0.71.
1.2 边界条件太阳能烟囱内除进、出口和吸热壁面均采用绝热绝质的速度无滑移边界条件:
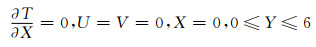 (7)
(7)
 (8)
(8)
进、出口处边界条件:
 (9)
(9)
 (10)
(10)
吸热壁面的边界条件:
 (11)
(11)
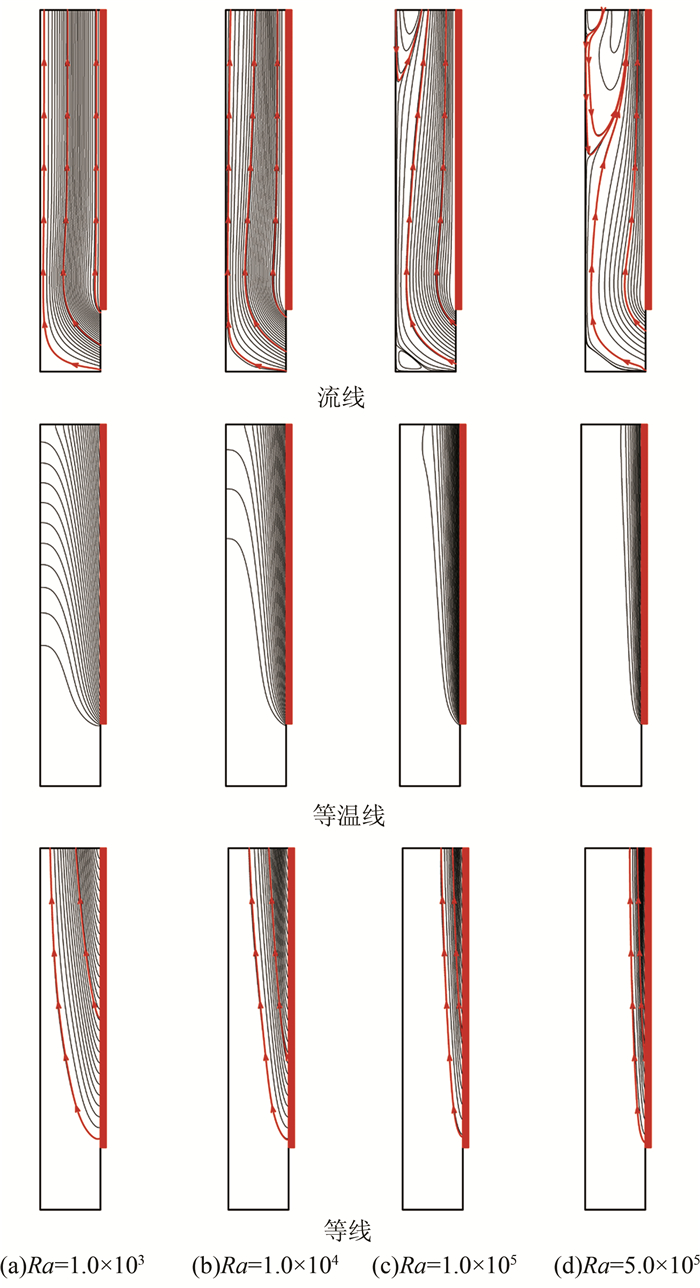
图 2描述了在不同Ra下烟囱内的流线、等温线和热线.从流线图中可以看出,当Ra=1.0×103和Ra=1.0×104时,空气沿水平进口进入后折转向上,其后流线与烟囱垂直壁面平行.当Ra=1.0×105和Ra=5.0×105,空气沿水平进口进入后,折转向上被卷吸进热边界层,沿着吸热壁面向上流动.随着Ra增大,热边界层从上游和下游卷吸空气的能力增强,在下游卷吸空气就导致了在烟囱出口处回流的出现,并且回流穿透深度随着Ra增大逐渐增大.等温线表明,当Ra=1.0×103和Ra=1.0×104时,对流换热强度较弱,热边界层厚度拓展到整个烟囱宽度,在烟囱内没有明显的热边界层,因此烟囱内的换热以导热为主导.随着Ra增大,热壁面附近出现明显的热边界层,并且厚度逐渐变薄.此时烟囱内的换热以对流换热为主导.热线图表明,热量沿着热壁面向出口处传递.随着Ra增大,热壁面热量向上传输路径逐渐变短,热量传输通道变窄.
|
| 图 2 不同Ra下烟囱内的流线、等温线和热线 Figure 2 Contour maps of streamlines, isotherms, and heatlines at different values of Ra number |
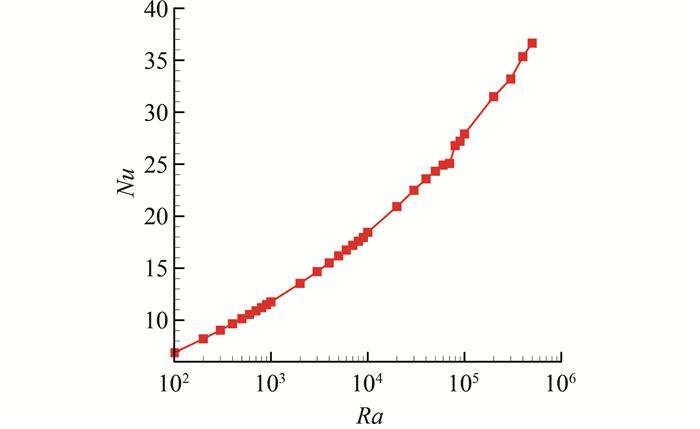
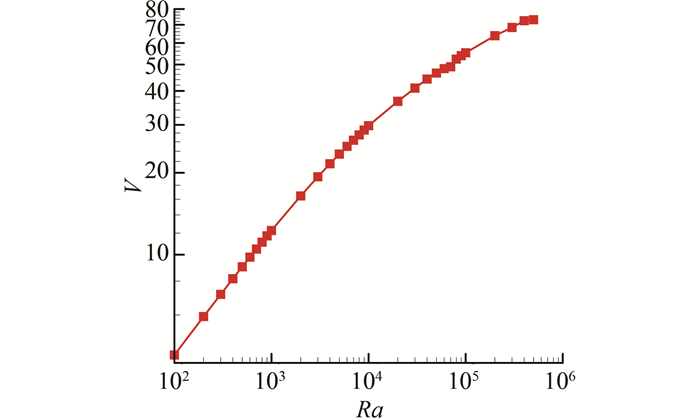
图 3描述了在不同Ra下烟囱内对流换热强度变化.从图中可以看出随着Ra增大,Nu数逐渐增大,烟囱内热壁面对流换热强度逐渐增强,图 2中等温线所示温度边界层越来越薄也说明对流强度随着Ra的增大而增强.图 4描述了不同Ra下烟囱内空气的无因次体积流量变化.从图 4可以看出,无因次体积流量随着Ra增加而增加,然而,当Ra大于某一定值时,体积流量增加率却下降.其原因是在高Ra情况下在烟囱出口处出现了回流.
|
| 图 3 不同Ra下烟囱内对流换热强度 Figure 3 Overall heat transfer rate as functions of Ra number |
|
| 图 4 不同Ra下烟囱内无因次体积流量 Figure 4 Dimensionless volume flow rate as functions of Ra number |
图 5描述了不同Ra下烟囱出口处无因次空气速度分布.从图中可以看出,出口处速度分布不均匀.当Ra < 104, 从左至右速度逐渐增大,到接近热壁面某一位置后速度逐渐减小.由于温度边界层厚度拓展至烟囱宽度,热壁面的传热在烟囱内部以导热为主,因此流体在热浮升力作用下在出口处速度从左至右逐渐增大,由于壁面的摩擦阻力到某一位置后速度逐渐减小,至壁面处为零.当Ra=105和Ra=5.0×105,出口处出现回流,因此速度在左侧呈现负值.随着Ra增大,向下的速度逐渐增大,至最大后逐渐减小至0.其后向上流动的空气速度从零增至最大后由于壁面的摩擦阻力减小至零.随着Ra增大,最大速度值也逐渐增大,并且出现位置逐渐向右移动,这是由于热边界层逐渐变薄,使得流线不断向右倾斜导致出口处最大速度值也随之向右移动.
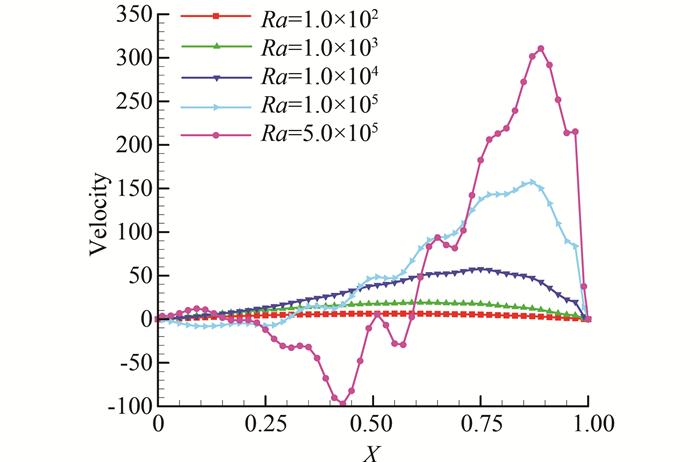
|
| 图 5 不同Ra下烟囱出口处无因次空气速度分布 Figure 5 Dimensionless velocity distributions across the chimney gap at outlet at different values of Ra number |
图 6描述了Ra=5.0×105,左侧热源高度D0分别从上至下和从下至上逐渐增加对吸热壁面Nu数和左侧热源表面Nu数的影响.实线和虚线分别表示吸热壁面和左侧热源表面的Nu数随D0的变化.从图中可以看出,相同D0,当其小于4时,从下至上增加比从上至下增加左侧热源高度D0吸热壁面Nu数大.当其大于4时,两种不同左侧热源高度增加方式吸热壁面的Nu近似相等;对于左侧热源表面的Nu数,从上至下增加热源高度D0比从下至上增加高度其表面的Nu大,表明热源从上部置于玻璃内表面更有利于其散热,由于在热浮升力作用下,上部的对流换热强度增强.

|
| 图 6 左侧热源高度D0从上至下和从下至上逐渐增加对吸热壁面和左侧热源表面Nu数的影响 Figure 6 Nu numbers of absorber and left heat source as functions of the left heat source height D0 |
图 7描述了左侧热源高度D0从上至下和从下至上增加对烟囱内诱导无因次体积流量的影响.图中曲线表明,相同的热源高度D0,不同的放置位置诱导的体积流量不同,从下至上比从上至下逐渐增大其高度,诱导的体积流量大.另外当D0 > 1,体积流量的增加率降低.鉴于此,本文将利用此结果将D0=1热源从下至上放置试图寻找其较优的位置,有效避免回流,实现流量的最大化.
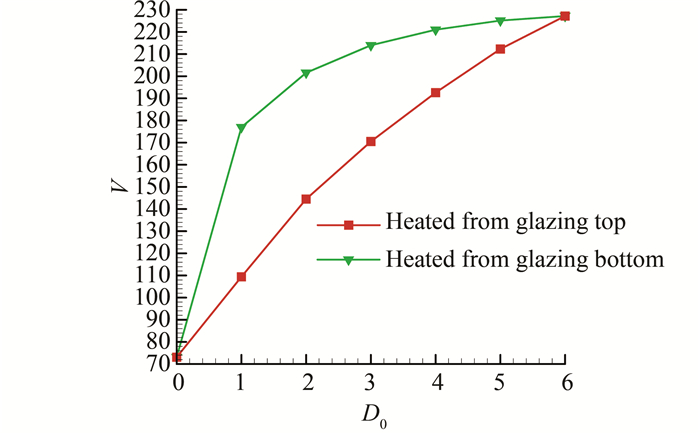
|
| 图 7 左侧热源高度D0从上至下和从下至上增加对烟囱内诱导无因次体积流量的影响 Figure 7 Dimensionless volume flow rates as functions of the left heat source height D0 |
图 8为D0=1的热源,在Ra=5.0×105时,流线、等温线和热线随S0的变化图.从流线图中可以看出,随着S0增大,流线逐渐发生扭曲,出口处均未出现回流.等温线表明吸热壁面和左侧热源表面均形成明显的温度边界层,随着S0增大,左侧热源表面等温线向上移动,而吸热壁面的等温线变化很小.热线呈现和等温线类似的变化趋势,热量从热源表面向上往出口处传输.

|
| 图 8 D0=1的热源,在Ra=5.0×105时,流线、等温线和热线随着S0的变化 Figure 8 Contour maps of streamlines, isotherms, and heatlines as functions of S0 at D0=1 and Ra=5.0×105 |
图 9为N=2、D0=D1=0.5的离散热源,当S0=0、Ra=5.0×105保持不变时,流线、等温线和热线随着S1的变化图.从流线图中可以看出,随着S1增大,流线发生轻微扭曲,程度较N=1时弱,出口处均未出现回流.等温线表明吸热壁面等温线在不同S1时变化很小,离散热源表面的等温线也在各自表面形成明显的温度边界层.热线表明热量从各个热表面向上向出口方向传输.

|
| 图 9 N=2, D0=D1=0.5的离散热源,在Ra=5.0×105时,流线、等温线和热线随着S1的变化 Figure 9 Contour maps of streamlines, isotherms, and heatlines as functions of S1 at N=2, D0=D1=0.5 and Ra=5.0×105 |
图 10为离散热源数目和位置变化对烟囱内诱导空气无因次体积流量的影响.从图中可以看出,Ra=5.0×105,N=1,D0=1,随着S0的增大,烟囱内诱导的空气量减少;N=2,D0=0.5,S0=0,随着S1的增大,烟囱内诱导的空气量也减少.但在N×D0值相同的情况下,N=2,S0=0时,在S1与N=1中S0(S0 > 0)的值相等时,N=2诱导的空气量大于N=1时诱导的空气量.
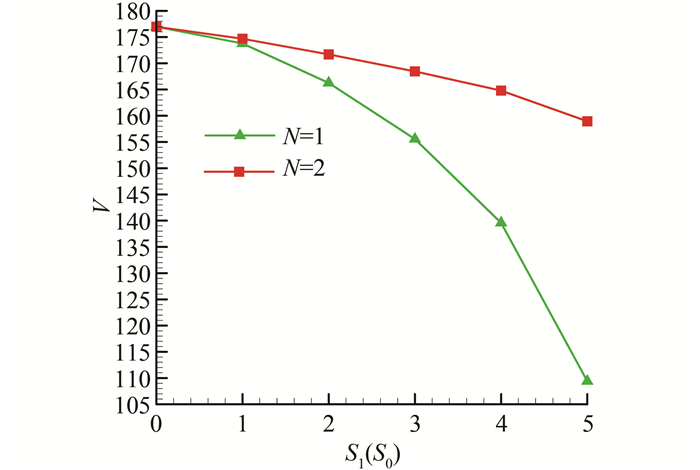
|
| 图 10 离散热源数目和位置变化对烟囱内诱导空气无因次体积流量的影响 Figure 10 Dimensionless volume flow rates at different values of N, S0 and S1 |
本文数值分析了不同Ra下太阳能烟囱通风性能,通过探讨玻璃侧离散热源位置和高度,有效解决了其内部回流并大大提高了烟囱通风量,主要结论如下:
1) 当Ra > 105,温度边界层厚度小于太阳能烟囱宽度,在其出口处出现回流,导致流量增加率降低.
2) 流线和热线实现了烟囱内空气流动和热量传递的可视化,描述了出口处回流的穿透深度和热量传递路径,更直观地解释了边界层理论,为提高烟囱性能提供了有力的理论依据.
3) 在Ra=5.0×105的情况下,N=1,从下至上逐渐增加D0与从上向下逐渐增加其值相比,所诱导的体积流量更大.因此减少烟囱回流,提高烟囱流量,优化左侧热源位置应从玻璃下部开始寻找.
4) D0=1的热源,在Ra=5.0×105时,太阳能烟囱诱导的无因次体积流量随着S0的增大而减小;D0=0.5,N=2的热源,在S0=0,Ra=5.0×105时,太阳能烟囱诱导的无因次体积流量随着S1的增大而减小.因此D0=1,S0=0,在Ra=5.0×105时,太阳能烟囱诱导的无因次体积流量最大.而在N×D0值相同的情况下,N=2时,在S1与N=1中S0(S0 > 0)的值相等时,N=2诱导的空气量大于N=1时诱导的空气量.
| [1] | Barozzi C S, Imbabi M S E, Nobile E, Sousa A C M. Physical and numerical modeling of a solar chimney-based ventilation system for buildings[J]. Building and Environment, 1992, 27: 433–445. DOI:10.1016/0360-1323(92)90042-N |
| [2] | Bansal N K, Mathur R, Bhandari M S. Solar chimney for enhanced stack ventilation[J]. Building and Environment, 1993, 28: 373–377. DOI:10.1016/0360-1323(93)90042-2 |
| [3] | Khedari J, Hirunlabh J, Bunnag T. Experimental study of a roof solar collector towards the natural ventilation of new houses[J]. Energy and Buildings, 1997, 26: 159–164. DOI:10.1016/S0378-7788(96)01030-4 |
| [4] | Ong K S, Chow C C. Performance of a solar chimney[J]. Solar Energy, 2003, 74: 1–17. DOI:10.1016/S0038-092X(03)00114-2 |
| [5] | Chantawong P, Hirunlabh J, Zeghmati B, et al. Investigation on thermal performance of glazed solar chimney walls[J]. Solar Energy, 2006(80): 288–297. |
| [6] | Khanal R, Lei C W. Solar chimney—A passive strategy for natural ventilation[J]. Energy and Buildings, 2011(43): 1811–1819. |
| [7] | Zhai X Q, Song Z P, Wang R Z. A review for the application of solar chimneys in buildings[J]. Renewable and Sustainable Energy Reviews, 2011(15): 3757–3767. |
| [8] | Liu B, Ma X Y, Wang X L, et al. Experimental study of the chimney effect in a solar hybrid double wall[J]. Solar Energy, 2015(115): 1–9. |
| [9] | JingH W, Chen Z D, Li A G. Experimental study of the prediction of the ventilation flow rate through solar chimney with large gap-to-height ratios[J]. Building and Environment, 2015(89): 150–159. |
| [10] | Gan G, Riffat S B. A numerical study of solar chimney for natural ventilation of building with heat recovery[J]. Applied Thermal Engineering, 1998(18): 1171–1187. |
| [11] | Chen Z D, Bandopadhayay P, Halldorsson J, et al. An experimental investigation of solar chimney model with uniform wall heat flux[J]. Building and Environment, 2003(38): 893–906. |
| [12] | Jing H W, Li A G. Experimental study of vertical channel solar chimney with uniform heat flux for natural ventilation in building[J]. Advanced Materials Research, 2012, 374-377: 585–589. |
| [13] | Gan G. Simulation of buoyancy-induced flow in open cavities for natural ventilation[J]. Energy and Building, 2006(38): 410–420. |
| [14] | Khanal R, Lei C W. Flow reversal effects on buoyancy induced air flow in a solar chimney[J]. Solar Energy, 2012(86): 2783–2794. |
| [15] | Khanal R, Lei C W. An experimental investigation of an inclined passive wall solar chimney for natural ventilation[J]. Solar Energy, 2014(107): 461–474. |
| [16] | Silva A K da, Lorenzini G, Bejan A. Distribution of heat sources in vertical open channels with natural convection[J]. International Journal of Heat and Mass Transfer, 2005(48): 1462–1469. |
| [17] | Silva A K da, Lorente S, Bejan A. Constructal multi-scale structures for maximal heat transfer density[J]. Energy, 2006(31): 620–635. |
| [18] | Zhao F Y, Liu D, Tang G F. Application issues of the streamline, heatline and massline for conjugate heat and mass transfer[J]. International Journal of Heat and Mass Transfer, 2007(50): 320–334. |
| [19] | Ren X H, Hu J T, Liu D, et al. Vented enclosure under different flow schemes: Parametric investigations and non unique flow solutions[J]. Applied Thermal Engineering, 2016(94): 159–169. |
 2017, Vol. 50
2017, Vol. 50




