文章信息
- 徐青, 黄少奇, 李馨馨
- XU Qing, HUANG Shaoqi, LI Xinxin
- 水泥基材料含水量评价方法研究
- Study of water content evaluation method for cement-based materials
- 武汉大学学报(工学版), 2019, 52(2): 125-130
- Engineering Journal of Wuhan University, 2019, 52(2): 125-130
- http://dx.doi.org/10.14188/j.1671-8844.2019-02-004
-
文章历史
- 收稿日期: 2018-06-11
水泥基材料如混凝土或水泥砂浆,其含水量与水化作用密切相关,是影响混凝土强度、力学特性及耐久性的重要因素之一[1, 2].混凝土在浇筑过程及浇筑完成后,由于表面水分蒸发和水泥水化消耗,自由水含量减少,因此在标准湿度温度条件下的养护是保证混凝土质量的关键.水工混凝土结构通常在水下服役,结构中的水既能引起混凝土耐久性降低,同时它又是侵蚀性介质传输的载体[3, 4].因此,测定混凝土结构内部含水量及水分分布、水分动态迁移过程等,对混凝土结构质量评价具有重要意义.
国内外学者已采用多种方法检测水泥基材料的内部含水量.1979年,Gummerson等[5]采用核磁共振技术(NMR)检测混凝土非饱和吸水过程内部水分分布,得到试件不同时刻含水量分布曲线. 1981年,Rucker[6]认为,采用核磁共振技术检测混凝土内部含水量,测试结果易受顺磁性离子的干扰.1989年,Quenard等[7]采用射线透射法测量混凝土含水量时发现,当含水量较高时,结果的可靠性降低.2007年,沈春华[8]采用交流电测试技术判断水分传输前锋.2011年,张鹏等[9]采用中子成像技术对水泥基材料毛细吸水过程进行可视化定量检测.2015年,黄义建[10]利用压电传感器检测混凝土含水量,具有较好的抗电磁干扰效果,但检测信号受压电片距离等因素影响.2017年,李馨馨等[11]对混凝土中水分传输特性开展了细观理论模型、试验研究及数值模拟等一系列有意义的探索.
利用超声波检测技术测定脆性模型材料的力学性能,是原武汉水利电力学院在20世纪80年代首先提出并采用的方法.研究人员通过调整材料组分,做了大量的材料试验,得到超声波纵波波速、横波波速与脆性模型材料变形模量、凝聚力、内摩擦角以及动弹模、动泊松比等之间的相关关系,并提出了一些经验公式,为随后开展的水电工程试验研究提供了基础依据[12].
近年来,一些学者开展了超声波检测混凝土含水量的试验研究.例如,商涛平等[13]、申鲁[14]通过试验发现超声波速随着含水率的增大而增大;闫国亮等[15]研究了含水率与受损伤混凝土超声波速的关系;郑丹等[16]研究了检测频率与含水量对超声波速测量的影响.
1 技术路线及试件制备 1.1 技术路线本文结合物理模型试验和数值模拟分析两种研究手段,提出含水量与超声波速之间的经验公式,并以吸水试验为依据,获得材料的湿润前锋和非饱和渗透参数,如吸水率、水分扩散系数函数等.基于描述非饱和渗流运动的Richard方程,开展水泥基材料湿润前锋及含水量研究.模型试验与数值分析互为基础并相互验证,技术路线如图 1所示.
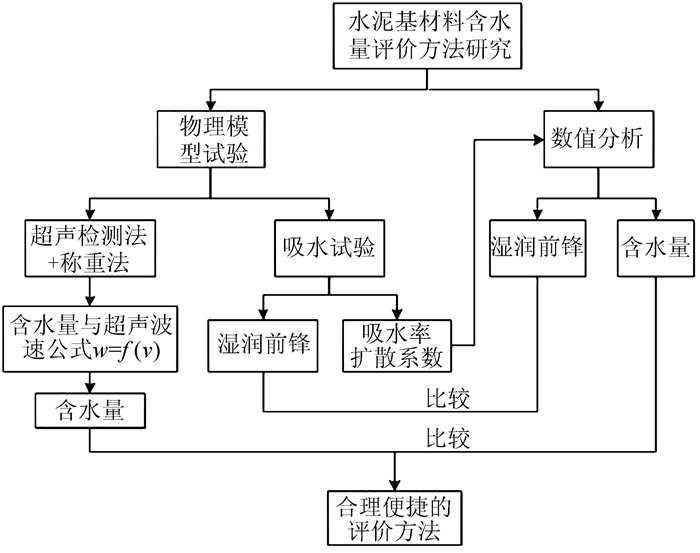
|
| 图 1 水泥基材料含水量评价方法研究技术路线 Fig. 1 Research procedure of water content of cement-based materials |
模型试验采用亚东牌P.O42.5普通硅酸盐水泥、标准砂和自来水,配合比采用C:W:S=1:0.45:2.依据SL352-2006《水工混凝土试验规程》制备试件,养护箱中标准养护28 d.
本文以2组试件为例,每组6个,尺寸均为150 mm×150 mm×150 mm,编号分别为A1~A6和B1~B6.
2 超声检测法研究混凝土含水量 2.1 超声检测原理超声脉冲波在混凝土中传播时,其传播速度与混凝土的密实程度有直接关系.对于原材料、配合比、龄期及测试距离等一定的混凝土,声速高则混凝土密实,声速低则混凝土相对不密实.不同成分的声阻抗率不同,如空气的声阻抗率远小于混凝土的声阻抗率.因此,脉冲波在混凝土中传播时,遇着孔隙或裂缝,将在其界面发生反射和散射,声能衰减.频率越高的成分衰减越快.随着混凝土中含水量增大,水分逐步填充内部孔隙或裂缝,超声波速随之增大.
2.2 试验步骤1) 将标准养护28 d的试件放置在烘箱中,恒温105 ℃,烘干至24 h内水分含量变化小于0.1%[17],认为此时混凝土内部含水量为0,相应试件质量为m0.
2) 取出烘干试件A1~A6,以浇筑试件的侧面作为测试面.在一对测试面上标示出9个测试点,测点编号如图 2所示.
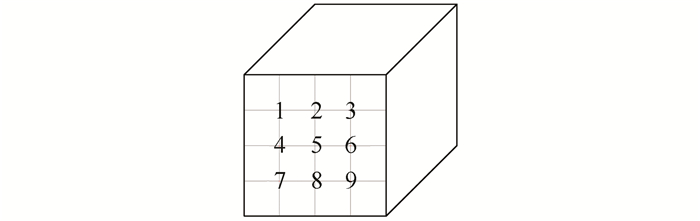
|
| 图 2 试件测点编号示意图 Fig. 2 Schematic illustration of samples numbering |
3) 待试件自然冷却至20 ℃,利用非金属超声波检测仪对试件进行超声检测并记录.
4) 将试件完全浸没在水中,经历0.5、1、2、4、6.5、9、12.5和48 h, 分别对各试件称重,并测定相应时刻各试件的超声波速.
2.3 试验结果分析称重法得到的不同时刻含水量(占试件质量的比值)如表 1所示.
| 时间/h | 含水量 | 平均含水量 | |||||
| A1 | A2 | A3 | A4 | A5 | A6 | ||
| 0.0 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.5 | 0.032 | 0.034 | 0.031 | 0.034 | 0.035 | 0.039 | 0.034 |
| 1.0 | 0.047 | 0.049 | 0.045 | 0.050 | 0.049 | 0.055 | 0.049 |
| 2.0 | 0.068 | 0.068 | 0.062 | 0.070 | 0.068 | 0.074 | 0.068 |
| 4.0 | 0.097 | 0.095 | 0.088 | 0.097 | 0.093 | 0.101 | 0.095 |
| 6.5 | 0.121 | 0.118 | 0.110 | 0.120 | 0.115 | 0.124 | 0.118 |
| 9.0 | 0.139 | 0.135 | 0.127 | 0.136 | 0.132 | 0.143 | 0.135 |
| 12.5 | 0.154 | 0.150 | 0.142 | 0.150 | 0.148 | 0.152 | 0.149 |
| 48.0 | 0.173 | 0.169 | 0.166 | 0.167 | 0.171 | 0.166 | 0.169 |
试件A1~A6在不同平均含水量时对应的超声波速如表 2所示,图 3为超声波速与平均含水量关系曲线.可以看出,超声波速随含水量增大而增大.
| 平均含水量 | 波速/(km·s-1) | 均方差 | 离差系数 | ||||||
| A1 | A2 | A3 | A4 | A5 | A6 | 均值 | |||
| 0.000 | 3.761 | 3.744 | 3.765 | 3.768 | 3.751 | 3.765 | 3.759 | 0.009 | 0.002 |
| 0.034 | 3.772 | 3.760 | 3.772 | 3.772 | 3.797 | 3.768 | 3.744 | 0.011 | 0.003 |
| 0.049 | 3.796 | 3.801 | 3.782 | 3.796 | 3.800 | 3.807 | 3.797 | 0.008 | 0.002 |
| 0.068 | 3.807 | 3.794 | 3.782 | 3.807 | 3.794 | 3.803 | 3.798 | 0.009 | 0.002 |
| 0.095 | 3.803 | 3.803 | 3.796 | 3.800 | 3.826 | 3.807 | 3.806 | 0.010 | 0.003 |
| 0.118 | 3.814 | 3.814 | 3.804 | 3.818 | 3.825 | 3.821 | 3.816 | 0.007 | 0.002 |
| 0.135 | 3.818 | 3.821 | 3.818 | 3.825 | 3.843 | 3.832 | 3.826 | 0.009 | 0.002 |
| 0.149 | 3.850 | 3.851 | 3.846 | 3.839 | 3.862 | 3.839 | 3.848 | 0.008 | 0.002 |
| 0.169 | 3.857 | 3.870 | 3.880 | 3.865 | 3.880 | 3.865 | 3.870 | 0.008 | 0.002 |
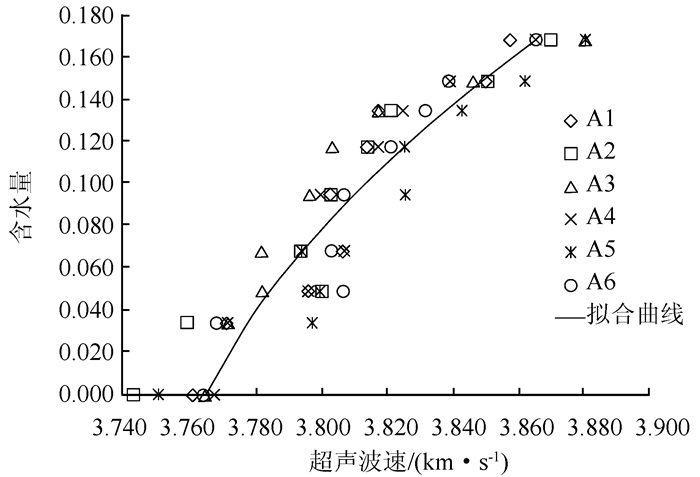
|
| 图 3 含水量与超声波速关系曲线 Fig. 3 Relationship between water content and ultrasonic wave velocity |
拟合含水量与超声波速之间的关系曲线,得到该配合比下砂浆试件超声波速与含水量的经验公式如下:
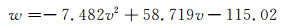 (1)
(1)
式中:w为试件的含水量;v为超声波速.
公式(1)的决定系数r2=0.998,且由表 2显示的均方差和离差系数可知,公式(1)未出现高度异常值,说明拟合程度较好.
3 应用吸水理论研究混凝土含水量为了实现采用数值方法研究混凝土内部含水量,以及验证本文提出的含水量与超声波速拟合公式的合理性,下面基于非饱和吸水理论开展进一步研究.
3.1 非饱和吸水理论对于完全干燥的水泥基材料,毛细管吸力是水分传输的主要因素.描述水泥基材料吸水特性的一个重要参数是吸水率,在实验室可通过称重法得到:
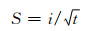 (2)
(2)
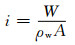 (3)
(3)
式中:S为水泥基材料的吸水率;i为材料单位面积上的累积吸水体积,即累积吸水深度;t为吸水时间;W为吸水质量;ρw为水的密度;A为试件吸水面的面积.
多孔介质中的饱和-非饱和渗流状态可采用扩展Darcy定律描述:
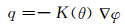 (4)
(4)
式中:q为渗透流速,m/s;K(θ)为非饱和渗透系数,m/s;θ为相对含水量,也称为有效饱和度;φ为总水头势,m.
相对含水量θ表示材料的饱和程度,θ=0~1,设材料初始为完全干燥状态,此时θ=0,至完全饱和状态时θ=1.θ计算式为
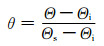 (5)
(5)
式中:Θ为体积含水量,是孔隙中水的体积与试件体积的比值;Θi和Θs分别为初始体积含水量和饱和体积含水量.
假定混凝土骨架不发生变形,并且水是不可压缩的,则连续性方程为
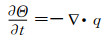 (6)
(6)
将扩展Darcy定律式(4)代入连续性方程式(6)中,可以得到以相对含水量为变量的混凝土饱和-非饱和Richard方程:
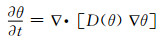 (7)
(7)
式中:D(θ)为非饱和水分扩散系数,m2/s.
当材料初始为完全干燥状态,将试件的一个面与水面完全接触,此时控制方程为
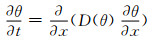 (8)
(8)
Parlange等[18]给出了式(8)非线性扩散方程的近似解析解:
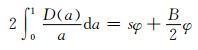 (9)
(9)
其中:
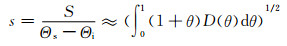 (10)
(10)
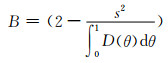 (11)
(11)
式中:s为相对吸水率;B为系数.
大量试验资料拟合结果表明,对于各种建筑材料如混凝土、砖、石等,水分扩散系数与相对含水量近似服从指数函数关系[19, 20]:
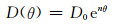 (12)
(12)
式中:D0为扩散系数的量值参数;n为扩散系数曲线的形状参数[19].
形状参数n值一般为6~8,与材料性能关系不大,不同配合比的混凝土试件n可以取相同值[20],本研究取n=6,将式(12)代入式(10),得到
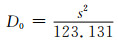 (13)
(13)
由称重法得到吸水率S后,根据式(10)、(12)和式(13),得到水分扩散系数函数D(θ)的表达式,代入控制方程(8),即可得到一定吸水时间t时试件不同部位的相对含水量θ.
3.2 吸水物理模型试验为了得到材料的吸水率S,在开展数值研究之前,先进行吸水物理模型试验.
3.2.1 试验步骤参考ASTM C 1585-04[21]标准进行毛细吸水试验.
1) 将完全烘干的试件B1~B6冷却至室温20 ℃,取出试件,迅速用保鲜膜密封除底面以外的其他5个面,底面浸水3~5 mm,进行吸水试验.试验装置如图 4所示.

|
| 图 4 毛细吸水试验装置 Fig. 4 Experimental setup of absorption test |
2) 每隔一段时间称重.
3) 48 h后利用压力试验机劈裂试件,测量吸水48 h时的水分渗透深度,图 5展示了试件B1的吸水深度.

|
| 图 5 试件B1吸水深度 Fig. 5 Penetration depths of wetting front within sample B1 |
试验得到累积吸水量i随时间t的变化曲线,如图 6所示.
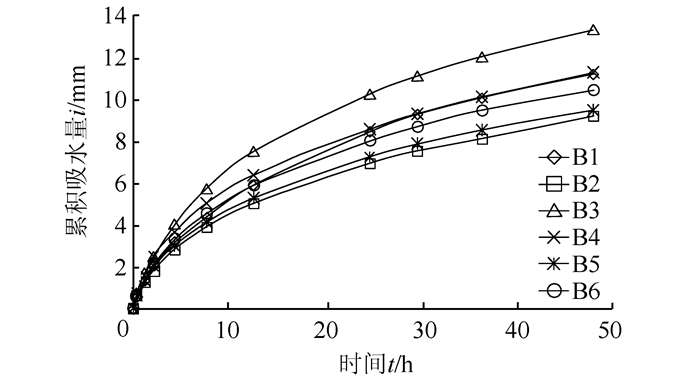
|
| 图 6 累计吸水量i与时间t关系曲线 Fig. 6 Relationships between cumulative water absorption and time |
从图 6可以看出,当砂浆试件底部与水面接触发生毛细吸水时,水分在短时间内即渗入试件内部.初期吸水量增加迅速,随着时间的推移,累积吸水量曲线斜率逐渐变缓.去掉一个最大值(B3)和一个最小值(B2),由式(2)、式(10)和式(13)可得到平均吸水率S=1.58 mm/h0.5、相对吸水率s=9.05 mm/h0.5和量值参数D0=0.70 mm2/h.
3.3 数值试验及分析基于上述非饱和吸水理论,对COMSOL软件进行二次开发,研究水泥砂浆试件毛细吸水过程及内部含水量.
数值模拟试件尺寸为150 mm×150 mm×150 mm,初始状态为完全干燥.
3.3.1 数值试验研究毛细吸水过程以试件B1为例,对底面吸水数值模拟进行分析.
1) 定解条件
初始条件: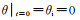
第一类边界条件: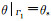
第二类边界条件: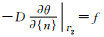
边界条件中:{n}={lx, ly, lz}T,是边界的外法向;f是第二类边界Γ2上的渗入流速,Γ2包括无流动边界和蒸发边界两种边界.
2) 数值试验结果及分析.不同吸水历时1、3、5、10、24、48 h,试件不同高度处水分含量分布曲线如图 7所示.
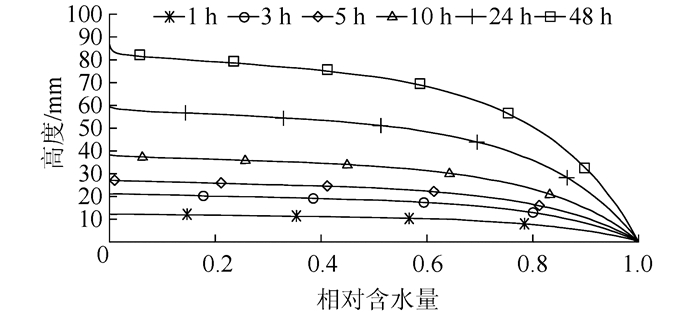
|
| 图 7 试件B1内部相对含水量分布曲线 Fig. 7 Water content distribution curve within the sample B1 |
随着吸水过程的进行,在毛细吸力作用下,水分逐渐侵入试件内部,越靠近水和试件的接触面,水分含量越高;随着时间的增加,试件含水量增加.48 h时物理模型试验和数值试验得到的吸水深度对比如表 3所示.
| mm | |||||||
| 试件编号 | B1 | B2 | B3 | B4 | B5 | B6 | |
| 吸水深度 | 数值试验 | 86 | 74 | 101 | 90 | 73 | 83 |
| 物理试验 | 87.2 | 78.3 | 96.5 | 83.8 | 78.8 | 84.3 | |
由表 3可以看出,数值试验和物理模型试验得到的吸水深度非常接近,数值方法可以合理便捷地分析水泥基材料的单面吸水过程,了解水分湿润前锋的位置,判断材料内部饱和、非饱和以及干燥区域的分布情况,该成果对判断混凝土坝体内部渗流场有很好的帮助.
3.3.2 数值试验研究含水量基于吸水试件平均参数,将数值试验得到的不同历时试件含水量与超声检测法得到的含水量进行对比,如图 8所示.
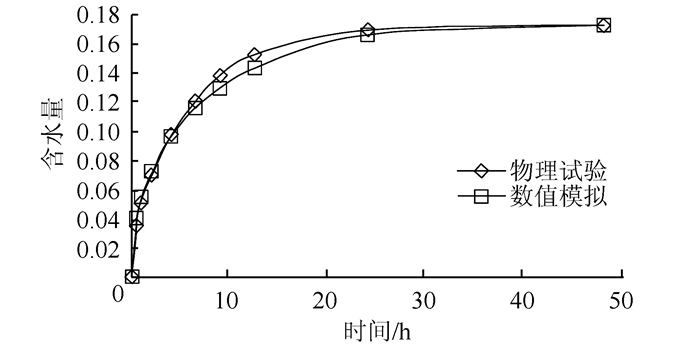
|
| 图 8 含水量变化曲线 Fig. 8 Water content variation curve |
由图 8可以看出,数值试验与物理模型试验吻合很好,说明数值试验可以方便地评估水泥基材料内部含水量的分布情况.
4 结论本文基于超声检测原理和非饱和吸水理论,采用物理模型试验和数值模拟分析两种途径研究水泥基材料内部含水量,以及在毛细吸力作用下,材料湿润前锋的渗透深度,定量研究了超声波速与含水量之间的关系,得到以下结论:
1) 随着水泥基材料含水量的增大,其孔隙内空气逐渐被排出,试件的超声波速逐渐增大,含水量与超声波速之间存在二次非线性关系.本研究基于超声检测试验,提出了含水量与超声波速之间的经验公式,并通过数值模拟分析验证了该经验公式的合理性.
2) 基于吸水试验获得的非饱和渗透参数,采用数值分析方法可以较好地评价水泥基材料内部吸水高度,以及试件内部不同部位含水量的分布.
3) 对于不同配合比、不同骨料级配及含量的混凝土,其内部含水量与超声波速之间的关系会有一些出入.本文研究成果旨在为评价实际混凝土结构工程,尤其是判断混凝土坝体内部渗流场提供一种便捷高效的方法,对实际混凝土结构工程具有一定的借鉴意义.
| [1] |
杨华全, 李文伟. 水工混凝土研究与应用[M]. 北京: 中国水利水电出版社, 2005. Yang Huaquan, Li Wenwei. Research and Application for Hydraulic Concrete[M]. Beijing: China WaterPower Press, 2005. |
| [2] |
陈胜宏, 何真. 混凝土坝服役寿命仿真分析的研究现状与展望[J]. 武汉大学学报(工学版), 2011, 44(3): 273-280. Chen Shenghong, He Zhen. Status quo and prospects for simulation analysis of service life for concrete dam[J]. Engineering Journal of Wuhan University, 2011, 44(3): 273-280. |
| [3] |
王立成. 建筑材料吸水过程中毛细管系数与吸水率关系的理论分析[J]. 水利学报, 2009, 40(9): 1085-1090. Wang Licheng. Analytical relationship between capillarity coefficient and sorptivity of building material[J]. Journal of Hydraulic Engineering, 2009, 40(9): 1085-1090. DOI:10.3321/j.issn:0559-9350.2009.09.009 |
| [4] |
王新友, 蒋正武, 高相东, 等. 混凝土中水分迁移机理与模型研究评述[J]. 建筑材料学报, 2002, 5(1): 66-71. Wang Xinyou, Jiang Zhengwu, Gao Xiangdong, et al. Review on the mechanism and model of moisture transfer in concrete[J]. Journal of Building Materials, 2002, 5(1): 66-71. DOI:10.3969/j.issn.1007-9629.2002.01.013 |
| [5] |
Gummerson R J, Hall C, Hoff W, et al. Unsaturated water flow within porous materials observed by NMR imaging[J]. Nature, 1979, 281(5726): 56-57. DOI:10.1038/281056a0 |
| [6] |
Rucker P. Redistribution of pore water in the cement gel of concrete[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 1981, 85(13): 2757-2764. |
| [7] |
Quenard D, Sallee H. A gamma-ray spectrometer for measurement of the water diffusivity of cementitious material[C]// Materials Research Society Symposium Proceedings, 1989, 137: 165-169.
|
| [8] |
沈春华.水泥基材料水分传输的研究[D].武汉: 武汉理工大学, 2007. Shen Chunhua. Researches on the moisture transport of cement-based materials[D].Wuhan: Wuhan University of Technology, 2007. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1365823 |
| [9] |
张鹏, 赵铁军, Wittmann F H, 等. 基于中子成像的水泥基材料毛细吸水动力学研究[J]. 水利学报, 2011, 42(1): 81-87. Zhang Peng, Zhao Tiejun, Wittmann F H, et al. Water capillary suction dynamics of cement-based materials based on neutron radiography method[J]. Journal of Hydraulic Engineering, 2011, 42(1): 81-87. |
| [10] |
黄义建.混凝土内部水分迁移过程监测与收缩变形机理研究[D].哈尔滨: 哈尔滨工业大学, 2015. Huang Yijian. Research on monitoring of water transportation in concrete and mechanism of shrinkage deformation[D]. Harbin: Harbin Institute of Technology, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10213-1015981958.htm |
| [11] |
Li Xinxin, Chen Shenghong, Xu Qing, et al. Modeling the three-dimensional unsaturated water transport in concrete at the mesoscale[J]. Construction and Building Materials, 2017, 190: 61-74. |
| [12] |
徐青, 李桂荣. 水工结构模型实验[M]. 武汉: 武汉大学出版社, 2015. Xu Qing, Li Guirong. Model Test for Hydraulic Structures[M]. Wuhan: Wuhan University Press, 2015. |
| [13] |
商涛平, 童寿兴. 混凝土超声检测中含水率对声速影响的研究[J]. 无损检测, 2003, 25(4): 189-191. Shang Taoping, Tong Shouxing. Study on the effect of the water content of concrete on the velocity of ultrasonic waves[J]. Nondestructive Testing, 2003, 25(4): 189-191. DOI:10.3969/j.issn.1000-6656.2003.04.006 |
| [14] |
申鲁.非破损法检测潮湿混凝土抗压强度试验研究[D].郑州: 郑州大学, 2005. Shen Lu. Experimental research on compressive strength test of humid concrete with nondestructive methods[D]. Zhengzhou: Zhengzhou University, 2005. http://cdmd.cnki.com.cn/Article/CDMD-10459-2005138980.htm |
| [15] |
闫国亮, 赵庆新. 含水率对受损混凝土超声波波速的影响[J]. 无损检测, 2009, 31(1): 48-49. Yan Guoliang, Zhao Qingxin. The effect of water content on the damage concrete ultrasonic detection[J]. Nondestructive Testing, 2009, 31(1): 48-49. |
| [16] |
郑丹, 任涛. 频率及含水量对混凝土损伤超声检测的影响[J]. 水利学报, 2014(S1): 90-94. Zheng Dan, Ren Tao. Influence of frequency and water content on ultrasonic damage testing in concrete[J]. Journal of Hydraulic Engineering, 2014(S1): 90-94. |
| [17] |
Belleghem B V, Montoya R, Dewanckele J, et al. Capillary water absorption in cracked and uncracked mortar-A comparison between experimental study and finite element analysis[J]. Construction & Building Materials, 2016, 110: 154-162. |
| [18] |
Parlange J Y, Lisle I G, Prasad S N, et al. Wetting front analysis of the nonlinear diffusion equation[J]. Water Resources Research, 1984, 20(5): 636-638. DOI:10.1029/WR020i005p00636 |
| [19] |
Leech C, Lockington D, Dux P. Unsaturated diffusivity functions for concrete derived from NMR images[J]. Materials and Structures, 2003, 36(6): 413-418. DOI:10.1007/BF02481067 |
| [20] |
Hall C. Water sorptivity of mortars and concretes: a review[J]. Magazine of Concrete Research, 1989, 41(147): 51-61. DOI:10.1680/macr.1989.41.147.51 |
| [21] |
ASTM C 1585-2004 Standard Test Method for Measurement of Rate of Absorption of Water by Hydraulic Cement Concretes[S], 2002.
|
 2019, Vol. 52
2019, Vol. 52



