文章信息
- 李欣, 刘美秀, 刘迪
- LI Xin, LIU Meixiu, LIU Di
- 复杂背景下高层建筑钢结构板孔心影像坐标量测
- Measurement of image coordinates of hole center in steel structure plate under complex background
- 武汉大学学报(工学版), 2016, 49(1): 143-147
- Engineering Journal of Wuhan University, 2016, 49(1): 143-147
- http://dx.doi.org/10.14188/j.1671-8844.2016-01-025
-
文章历史
- 收稿日期: 2015-07-05
近年来,基于图像的测量技术(如近景摄影测量、视觉测量、视觉检测等)已经广泛应用于许多领域中[1, 2],这主要是由于图像测量技术具有非接触、速度快、精度合适、现场抗干扰能力强等优点.针对钢结构板圆孔检测,确定圆孔中心在图像中的精确位置是采用上述方法的必要步骤.根据透视投影的固有特性,圆形目标经过透镜成像后变为椭圆.关于椭圆构像中心的研究方法有很多:灰度平方法、周长平均法[3]、Hough变换[4]等,这些方法通常对图像灰度的均匀分布有要求,在圆孔背景噪声比较大、测量环境复杂的情况下不宜采取.为了获得椭圆中心的精确坐标,不少研究学者也做了很多相关研究:文献[5]基于回光反射材料制作圆形标志,对标志的椭圆影像运用经典算法和梯度幅值均值法相结合进行边缘的亚像素提取,从而得到椭圆中心的子像素位置;基于Zernike矩的边缘亚像素定位方法[6]也取得了很高的精度.上述两种方法在测量环境较好的前提下可以获得很好的测量精度,比如文献[5]中的影像就是被测物影像清淡、标志点影像密度大而清晰的“准二值影像”,一旦变换成比较复杂的测量环境,并不能很好地发挥其精度优势.
本文研究对象是圆孔背景复杂的测量环境中使用数码相机拍摄的钢结构板图像,该图像的特点是图像范围大、背景杂乱;目标圆孔影像区域噪声大、圆孔边缘模糊.为达到即使在这样复杂的测量环境中也能获得圆孔中心在图像上的精确坐标的目的,采取了以下的方法:在钢结构板待测圆孔区域放置活动控制架,根据二维直接线性变换算法确定影像中圆孔中心的粗略位置,从而确定每个圆孔所属的ROI区域,在各ROI区域内进行图像二值化及形态学处理后,采用Canny算子检测椭圆的像素级边缘,对像素级边缘点用Zernike矩算子进行亚像素边缘检测;最后,对提取的亚像素级边缘点进行最小二乘椭圆拟合,确定圆孔中心的精确位置.该方法不仅保证了圆孔中心的测量精度,也适用于一些较复杂的环境中,做到了确保精度的同时扩大了适用范围.
1 图像预处理人类视觉系统在处理较为复杂的场景时,会将其视觉注意力集中于该场景的少数几个对象,并将这些对象优先处理,力求在最短时间获取场景中的主要信息,此过程称为视觉注意过程,这些对象在场景中构成的区域即为感兴趣区域(Region of interest,ROI).提取图像的ROI可大大降低图像处理时的计算量,也可以减少复杂背景对感兴趣区域的影响,因此对于处于复杂背景下的圆孔测量来说,ROI起着极其重要的作用.为了更有效地处理圆孔区域,对图像中每个圆孔设置其感兴趣区域,依次处理每个感兴趣区域,达到提取圆孔中心的目的.
1) 圆孔中心粗略坐标的计算:在钢结构板待测圆孔区域放置活动控制架,建立物方坐标系,如图 1所示,控制点坐标已知,将控制点的物方坐标和量测的像点坐标代入二维直接线性变换公式,计算得到8个二维直接线性变换系数(l1,l2,…,l8):

|
| 图 1 确定ROI图像 Figure 1 Images for ROI |
根据圆孔中心之间的设计距离以及圆孔在活动控制架中的相对位置关系,可确定圆孔中心的物方坐标近似值,再次使用式(1) ,可计算圆孔中心在图像上的近似坐标(x,y),可以作为ROI中心.
2) ROI的确定:图像上圆孔的大小基本一致,可将计算出的影像中的孔心近似坐标作为中心,绘制一包含此圆孔的矩形窗口,即为该圆孔的ROI.选取某一圆孔为样本,由人工确定包含此圆孔的矩形,将此矩形窗口大小作为该张图像所有圆孔感兴趣区域的大小.
3) 由于测量环境的不确定性,导致测量目标经常处于比较复杂的背景中,噪声较大,为了避免其对测量精度产生不必要的影响,必须采取更具适用性的图像处理方法.分析本文的测量环境,由于噪声的影响,圆孔影像区域上整体模糊,局部散布着一些小的噪声物体(如图 2(a) 所示),导致图像二值化后边界不平滑以及圆孔区域出现不规则的细小空洞(见图 2(b)).在ROI内,通过形态学的开闭运算消除其中的噪声,填充物体内的细小空洞,如图 2(c)所示.

|
| 图 2 图像处理过程 Figure 2 Images processing demonstration |
传统的边缘提取算法有Roberts算子、Prewitt算子、LOG算子、Sobel算子等[7-9],这些算子算法简单、易于实现,但是它们或者对图像中的噪声比较敏感,或者定位效果差,实际应用中效果并不明显.相比之下,基于最优化的Canny算子[10]具有信噪比大和检测精度高的优点,应用比较广泛.该方法的主要过程如下:利用高斯函数进行低通滤波,计算梯度的幅值及方向,对梯度幅值进行非极大值抑制,检测和连接边缘等.虽然前面已经对图像进行了预处理,大大减少了噪声对边缘提取的影响,但是仍有可能检测出少许比较小的杂乱边缘,针对此现象,本文对提取边缘的面积进行阈值限制,面积阈值设为感兴趣区域总面积的1/10,将小于该阈值的边缘轮廓过滤掉,从而达到最优的边缘提取效果.如图 3所示,分别为阈值限制前的边缘图像和经过阈值限制后的边缘图像.

|
| 图 3 边缘面积阈值限制前后图像 Figure 3 Images before and after area threshold limits |
Zernike矩源于Teague提出的正交矩思想[11],相比于其他方法的优点是:它是正交矩,能够构造任意的高阶矩;它是一种积分运算,对噪声不太敏感.Teague以复域Zernike多项式为基,得到了具有正交、旋转不变特性的Zernike矩,在离散条件下,图像f(x,y)的二维Zernike矩在x2+y2≤1条件下可以定义为
其中:n≥0且n-|m|为偶数;*表示复共轭.
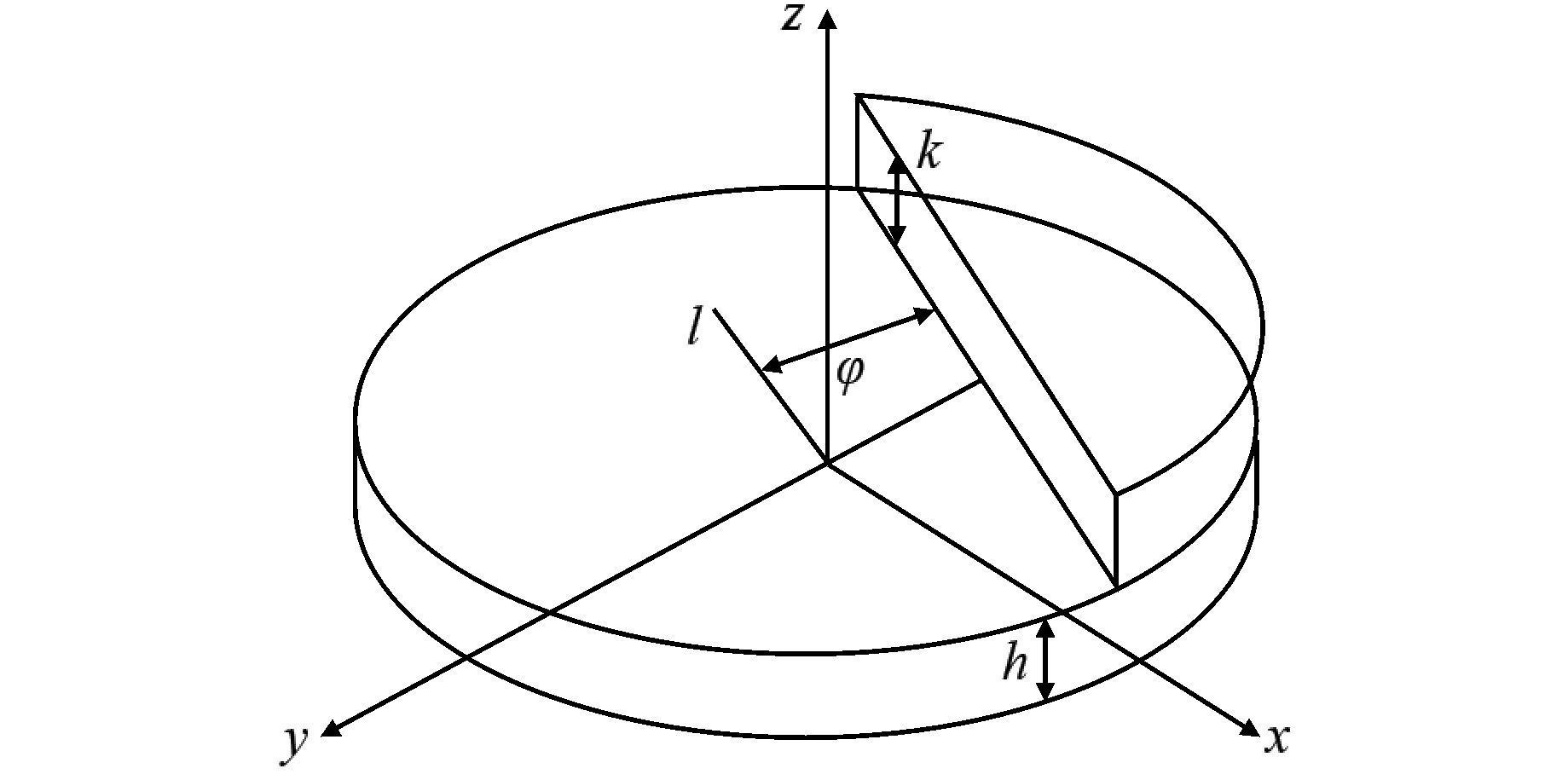
Ghosal和Mehrotal提出了利用Zernike矩检测边缘的算法[12],在该算法中建立了理想的阶跃灰度模型,通过图像的3个不同阶次Zernike矩计算各像素点的4个参数:k为灰度阶跃高度,h为背景灰度,l为中心点到边缘的距离,φ为中心点到边缘的垂线与x轴的夹角,具体物理意义见图 4,计算过程如下,并以这4个参数作为判断依据确定该像素点是否为边缘点.
|
| 图 4 亚像素边缘阶跃模型 Figure 4 Ideal step edge model for subpixel level edge |
如果像素点的图像参数l、k、h、φ满足条件k≥kt∩l2-l1≤lt(kt、lt为判断阈值)后,则该像素点为边缘点,进而可计算出边缘点的亚像素坐标:
其中:xs,ys是边缘的亚像素坐标;x,y表示图 4原点坐标;Zernike模版大小为N×N像素.
3 椭圆拟合及圆心坐标的确定圆形目标被摄影后,在影像上的投影为椭圆.根据确定的亚像素边缘点,进行最小二乘椭圆拟合,可确定圆心的影像坐标.椭圆的一般方程为
根据求得的(B,C,D,E,F)可以确定椭圆的5个参数:椭圆圆心坐标(xc,yc)、长短半轴(a,b)、长半轴与x轴夹角θ.其中圆心坐标的计算公式为
保证圆孔中心的定位精度,进一步剔除噪声对椭圆拟合的影响,采用多次椭圆拟合,逐步剔除非椭圆边界点,直至前后两次拟合椭圆的圆心坐标差值小于设定的阈值为止,取最后一次椭圆拟合计算的圆心坐标为该圆孔中心的影像坐标.
4 试验结果与分析试验目标为放置于室外地面的建筑物钢结构板,拍摄两组影像,一组为圆孔背景简单图像,如图 5所示,在圆孔下衬有黑板;另一组为圆孔背景复杂图像,如图 6所示,圆孔下背景为水泥地面.使用Nikon D90数码相机,镜头焦距18 mm,影像分辨率为4 288像素×2 848像素.对两组实验数据分别采用光束法平差方法计算圆孔物方坐标,因只关心其平面坐标,故以简单背景下计算的圆孔平面坐标为标准值,检验采用本文方法计算的复杂背景下钢板圆孔中心坐标的精度.

|
| 图 5 简单背景下的钢板图像 Figure 5 Images of steel plate under simple background |

|
| 图 6 复杂背景下的钢板图像 Figure 6 Images of steel plate under complex background |
如图 7所示为复杂背景下圆孔中心像点坐标量测效果,其中图 7(a)所示为全部像点量测的整体效果,图 7(b)为其中一个圆孔的椭圆拟合放大效果,可以看出拟合的椭圆与实际边缘很好地重合.

|
| 图 7 拟合效果图 Figure 7 Ellipse fitting image |
表 1所示为本文量测的复杂背景下的像点坐标经光束法平差计算后的各圆孔中心的中误差,其中mx、my分别表示x、y坐标的中误差,mxy表示圆孔中心点的平面中误差.经统计,x、y坐标方向的中误差分别为0.151、0.100 mm,各圆孔中心点位中误差为0.182 mm.
| 编号 | mx | mx | mxy |
| 1 | 0.093 | 0.112 | 0.146 |
| 2 | 0.128 | 0.100 | 0.162 |
| 3 | 0.222 | 0.122 | 0.253 |
| 4 | 0.112 | 0.096 | 0.148 |
| 5 | 0.169 | 0.090 | 0.191 |
| 6 | 0.096 | 0.094 | 0.134 |
| 7 | 0.124 | 0.095 | 0.156 |
| 8 | 0.207 | 0.090 | 0.226 |
根据光束法平差解算得到的两组圆孔中心的物方坐标及坐标差值如表 2所示,经统计,复杂背景下得到的孔心物方坐标与简单背景下得到的孔心物方坐标在x、y方向上的中误差分别为0.056和0.056 mm,dxy的中误差为0.079 mm.试验结果表明,本文方法在钢结构板圆孔背景复杂的情况下也能得到很好的定位精度.
| 编号 | 复杂背景下计算的孔心物方坐标 | 简单背景下计算的孔心物方坐标 | 坐标差 | ||||
| x | y | x | y | dx | dy | dxy | |
| 1 | 4 087.467 | 4 647.620 | 4 087.487 | 4 647.632 | 0.021 | 0.012 | 0.024 |
| 2 | 4 281.784 | 4 648.077 | 4 281.811 | 4 648.094 | 0.027 | 0.016 | 0.031 |
| 3 | 4 477.224 | 4 648.175 | 4 477.332 | 4 648.246 | 0.108 | 0.071 | 0.129 |
| 4 | 4 186.237 | 4 703.075 | 4 186.187 | 4 703.111 | -0.050 | 0.036 | 0.062 |
| 5 | 4 380.863 | 4 703.284 | 4 380.883 | 4 703.346 | 0.020 | 0.062 | 0.065 |
| 6 | 4 089.794 | 4 757.002 | 4 089.725 | 4 757.052 | -0.068 | 0.050 | 0.084 |
| 7 | 4 283.696 | 4 757.718 | 4 283.639 | 4 757.796 | -0.057 | 0.077 | 0.096 |
| 8 | 4 478.662 | 4 758.545 | 4 478.700 | 4 758.624 | 0.038 | 0.079 | 0.088 |
为了避免噪声对圆孔中心定位的影响,本文通过对复杂测量环境下的试验图像数据的分析,进行确定感兴趣区域、形态学、二值化等图像预处理,Canny算子和Zernike矩确定亚像素级边缘,并使用最小二乘拟合椭圆得到圆孔的椭圆构像中心.通过光束法平差计算各圆孔中心的点位误差以及两种环境下圆心物方空间坐标的比较,证实本文方法有着很好的圆心定位精度,可用于建筑钢板摄影测量质量检查中,解决复杂环境下钢板图像椭圆构像中心的定位问题,也可用于其他领域钢结构板孔心定位问题.
| [1] |
冯文灏.
近景摄影测量[M]. 武汉: 武汉大学出版社, 2002.
Feng Wenhao. Close-range Photogrammetry[M]. WuHan: Wuhan University Press, 2002. |
| [2] |
贾云得.
机器视觉[M]. 北京: 科学出版社, 2000.
Jia Yunde. Machine Vision[M]. BeiJing: Science Press, 2000. |
| [3] |
燕必希, 吕乃光, 邓文怡, 等. 数字近景摄影测量中几种靶点中心计算方法的比较[J].
光学精密工程, 2004, 12(4): 171–175.
Yan Bixi, Lü Naiguang, Deng Wenyi, et al. Comparison of several calculating methods of target image center in digital photogrammetry[J]. Optics and Precision Engineering, 2004, 12(4): 171–175. |
| [4] | Chen Yanxin, Qi Feihu. A new ellipse detection method using randomizedHough transform[J]. Journal of Infrared and Millimeter Waves, 2000, 19(1): 43–47. |
| [5] |
黄桂平. 圆形标志中心子像素定位方法的研究与实现[J].
武汉大学学报(信息科学版), 2005, 30(5): 388–391.
Huang Guiping. Center subpixel localization of circular retro-reflective targets[J]. Geomatics and Information Science of Wuhan University, 2005, 30(5): 388–391. |
| [6] | Liang Bo, Dong Mingli, Wang Jun, Yan Bixi. Sub-pixel location of center of target based on Zernike Moment [C]// Sixth International Symposium on Precision Engineering Measurements and Instrumentation, 2010. |
| [7] | Yan G P, Dai R Y, Pan Q, et al. Adaptive approach to image by Laplacian of Gaussian operator[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2008, 36(3): 85–102. |
| [8] | Marr D, Hildreth. Theory of edge detection [C]// Proceedings of the royal society of London. London, 1980: 187-217. |
| [9] | Information on http://en.wikipedia.org/wiki/Sobel_operator [EB/OL]. |
| [10] |
李二森, 张保明, 周晓明, 等. 自适应Canny边缘检测算法研究[J].
测绘科学, 2008, 33(6): 119–211.
Li Ersen, Zhang Baoming, Zhou Xiaoming, et al. Study on the self-adaptive Canny edge detection algorithm[J]. Science of Surveying and Mapping, 2008, 33(6): 119–211. |
| [11] | Teague M R. Image analysis via the general theory of moments[J]. Opt. Soc. Amer., 1980, 70: 920–93. DOI:10.1364/JOSA.70.000920 |
| [12] | Ghosal S, Mehrotra R. Orthogonal moment operators for subpixel edge detection[J]. Pattern Recognition, 1993, 26: 295–306. DOI:10.1016/0031-3203(93)90038-X |
 2016, Vol. 49
2016, Vol. 49



