文章信息
- 许晓勤, 陈淑梅
- XU Xiaoqin, CHEN Shumei
- 基于COMSOL PDE仿真的垂直板驻点混合对流与传热
- Mixed convection stagnation-point flow towards a stretching vertical sheet based on COMSOL
- 武汉大学学报(工学版), 2018, 51(3): 262-267
- Engineering Journal of Wuhan University, 2018, 51(3): 262-267
- http://dx.doi.org/10.14188/j.1671-8844.2018-03-013
-
文章历史
- 收稿日期: 2017-11-10
2. 福州大学机械工程及自动化学院,福建 福州 350116
2. School of Mechanical Engineering and Automation, Fuzhou University, Fuzhou 350116, China
具有延伸表面的边界层流动问题和传热问题常见于科学研究的诸多领域,比如冶金、化工和工业制造工艺中热轧、拔丝, 玻璃纤维和造纸, 塑料薄膜拉伸, 金属聚合物的挤出等[1].Hiemenz[2]首次介绍了二维驻点流,随后Homann[3]又把它扩展成轴对称流动并由Howarth[4]加以完善.Layek[5]等人研究了带有热源的多孔延伸板驻点流传热与传质问题.Bhattacharyya等人做了很多工作,主要研究带抽吸延伸板上驻点流磁流体边界层[6],过可渗透收缩板的MHD驻点流与传质问题[7],非均匀热流边界层驻点流传热问题[8]等.国内对这方面的研究比较少,但队伍在不断壮大,如Fan[9]等研究了收缩板上非定常驻点流与热传递,Xu[10]等研究了非定常延伸板上纳米液膜的流动与传热问题,Si[11]等研究多孔膨胀缸的非定常流动与传热问题.值得一提的是,上述文献所提的延伸板大多是线性延伸板,对垂直指数延伸板引起的驻点混合对流与传热问题的研究还未见报道.该类问题一般采用数值解法,如同伦分析法(HAM)[12]、Keller-box[13]、Crand-Nicolson法(CNM)[14]、打靶法[15]等.本文主要研究垂直指数延伸板驻点附近混合对流与传热问题,借助COMSOL软件自带的PDE模块来求解非线性常微分方程,利用参数扫描研究几个重要参数对驻点混合对流及传热特性的影响.
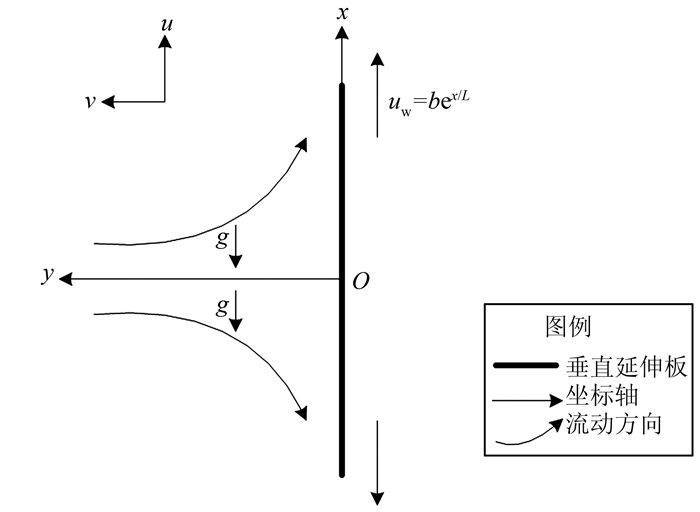
1 控制方程考虑二维不可压缩粘性流体在垂直指数延伸壁面上稳态的边界层流动与传热问题.模型示意图如图 1所示,x轴方向平行于壁面方向,y轴方向为垂直壁面方向, 壁面沿x方向延伸,速度uw=bex/L,u和v分别为沿着x和y方向的速度分量,L为参考长度,b为正的常数.
|
| 图 1 垂直指数延伸板二维驻点流的模型示意图 Figure 1 Schematic of the exponentially stretching vertical sheet system |
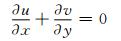 (1)
(1)
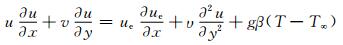 (2)
(2)
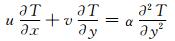 (3)
(3)
式中:g为重力加速度;υ为流体的运动粘度;β为热膨胀系数;T为流体温度;α为热扩散系数;ue=aex/L,为自由流速度;a为正的常数;T∞为外界温度.
边界条件:
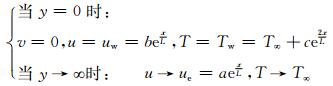 (4)
(4)
引入下列相似变量[18]:
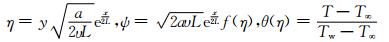 (5)
(5)
其中:ψ是流函数;Tw为壁面温度;c为正的常数.根据定义,可知速度分量为
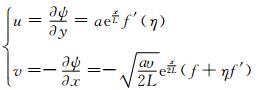 (6)
(6)
将速度分量代入方程(1)、方程(2)和方程(3),可知方程(1)自动满足,方程(2)和方程(3)分别简化如下:
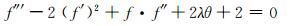 (7)
(7)
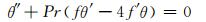 (8)
(8)
式中:Pr=υ/α,是Prandtl数;λ是浮力参数或混合对流参数,λ=GrL/(ReL)2.其中:GrL=gβ(Tw-T∞)L3/υ2,是格拉晓夫数[12, 13];ReL=ueL/υ,是雷诺数.注意λ=gβcL/a2,是常数,顺流时λ>0,逆流时λ < 0.
相应边界条件转化为
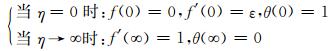 (9)
(9)
其中:ε=b/a,为速度比参数.
假定压缩功和摩擦热忽略不计,流体表面摩擦力系数和Nusselt数(表示对流换热强烈程度的一个准数)分别定义为
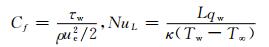 (10)
(10)
此处表面摩擦力τw与热通量qw可以分别写成:
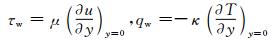 (11)
(11)
这里μ和κ分别表示动力粘度和导热系数.
利用相似变换式(5)可得:
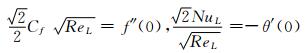 (12)
(12)
本文采用COMSOL软件自带的PED模块来求解非线性常微分方程(7)和(8).通过参数扫描研究几个重要的无量纲参数对流体流动和传热性能的影响.表 1和表 2分别给出当ε=1,λ=±1时不同的Pr对应的f″(0)和-θ′(0)值.图 2~11给出表面摩擦系数、Nusselt数、速度和温度分布曲线.
| Pr | f″(0) | |
| λ=1 | λ=-1 | |
| 0.72 | 0.496 342 041 490 532 20 | -0.524 500 643 108 940 10 |
| 1.00 | 0.455 989 386 505 311 96 | -0.478 232 200 563 322 60 |
| 6.80 | 0.243 651 161 855 769 52 | -0.247 525 927 543 961 20 |
| 10.00 | 0.209 427 965 876 948 00 | -0.211 967 988 813 938 75 |
| 20.00 | 0.156 530 461 635 771 45 | -0.157 664 201 499 041 92 |
| 40.00 | 0.114 214 107 776 266 62 | -0.114 695 293 082 608 17 |
| 60.00 | 0.093 880 538 819 306 03 | -0.094 166 824 617 506 25 |
| 80.00 | 0.081 220 646 773 861 20 | -0.081 417 391 677 167 22 |
| 100.00 | 0.072 328 043 376 757 02 | -0.072 474 683 080 891 11 |
| Pr | -θ′(0) | |
| λ=1 | λ=-1 | |
| 0.72 | 1.852 811 527 612 992 4 | 1.749 015 740 897 622 4 |
| 1.00 | 2.173 721 361 069 812 7 | 2.072 957 386 659 247 4 |
| 6.80 | 5.559 750 883 415 283 0 | 5.491 524 314 408 261 0 |
| 10.00 | 6.719 553 686 865 876 0 | 6.658 678 818 783 944 0 |
| 20.00 | 9.433 271 970 461 764 0 | 9.384 682 367 739 195 0 |
| 40.00 | 13.189 437 130 140 107 0 | 13.151 510 364 003 789 0 |
| 60.00 | 15.990 801 543 334 719 0 | 15.958 354 996 793 794 0 |
| 80.00 | 18.289 790 260 808 886 0 | 18.260 937 135 887 780 0 |
| 100.00 | 20.263 867 513 784 250 0 | 20.237 656 104 016 860 0 |
|
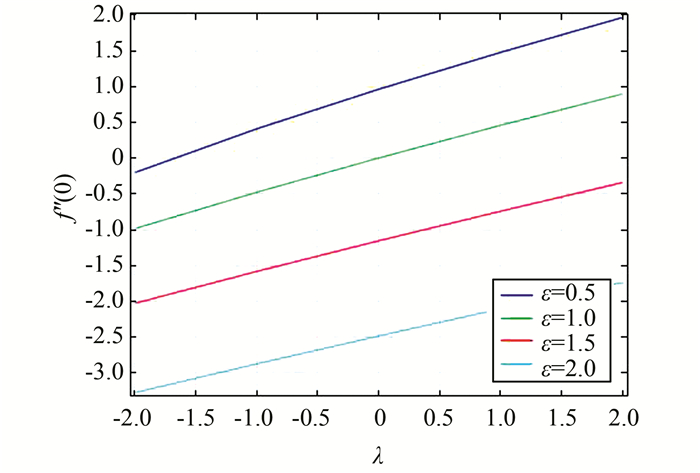
| 图 2 当Pr=1时,对应不同ε的f″(0)关于λ的函数图 Figure 2 Variation with λ of the skin friction coefficient for different values of ε when Pr=1 |
|
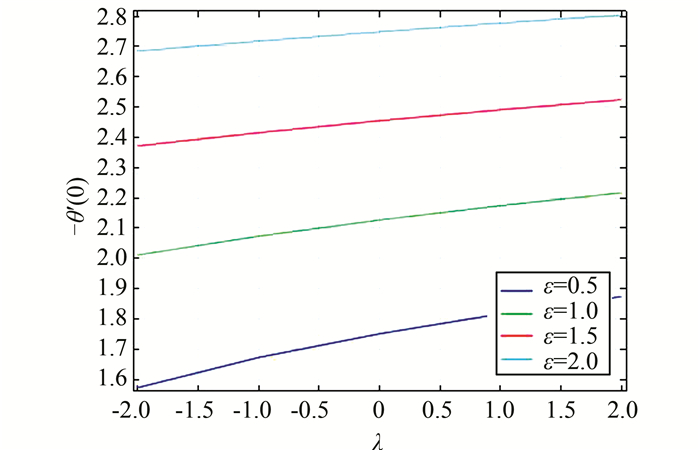
| 图 3 当Pr=1时,对应不同ε的-θ′(0)关于λ的函数图 Figure 3 Variation with λ of the Nusselt number for different values of ε when Pr=1 |
|
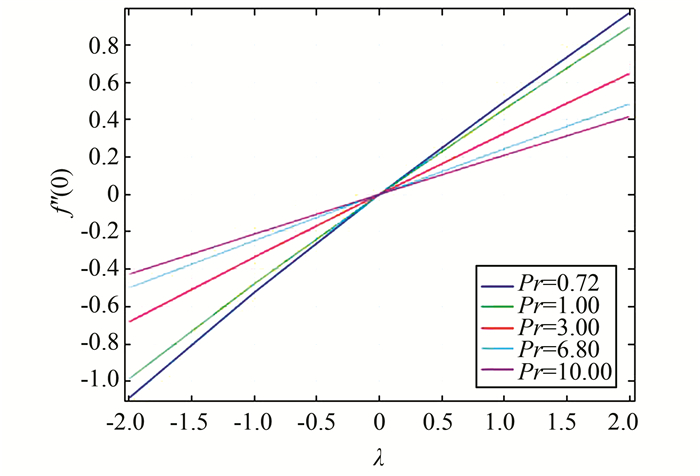
| 图 4 当ε=1时,对应不同Pr的f″(0)关于λ的函数图 Figure 4 Variation with λ of the skin friction coefficient for different values of Pr when ε=1 |
|
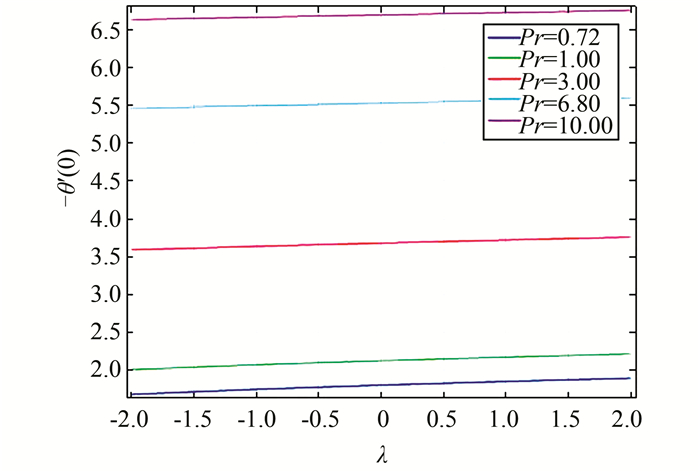
| 图 5 当ε=1时,对应不同Pr的-θ′(0)关于λ的函数图 Figure 5 Variation with λ of the local Nusselt number for different values of Pr when ε=1 |
|
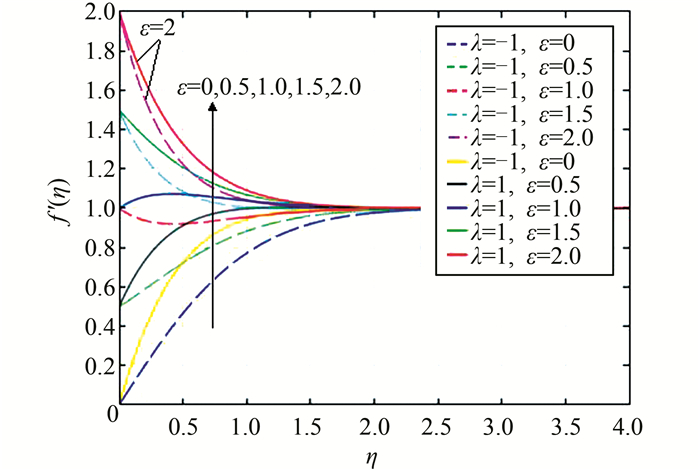
| 图 6 当Pr=1,λ=±1时,对应不同ε的速度分布图 Figure 6 Velocity profiles for different values of ε when Pr=1 and λ=±1 |
|
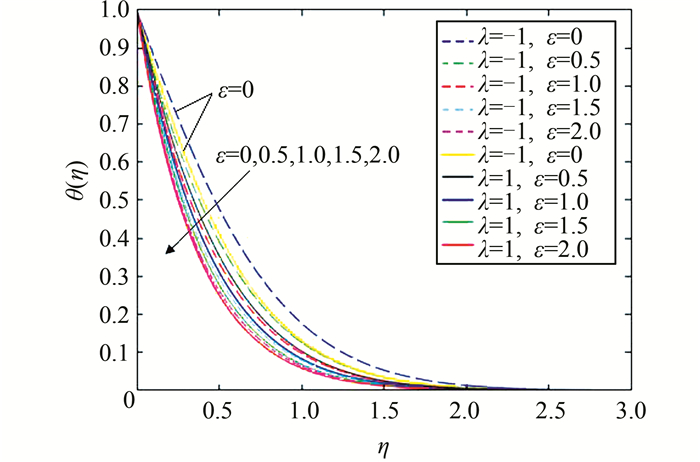
| 图 7 当Pr=1,λ=±1时,对应不同ε的温度分布图 Figure 7 Temperature profiles for different values of ε when Pr=1 and λ=±1 |
|
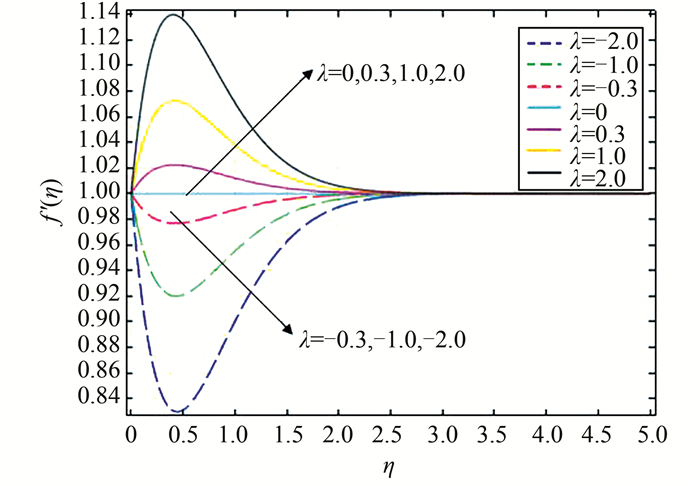
| 图 8 当Pr=1,ε=1时,对应不同λ的速度分布图 Figure 8 Velocity profiles for different values of λ when Pr=1 and ε=1 |
|
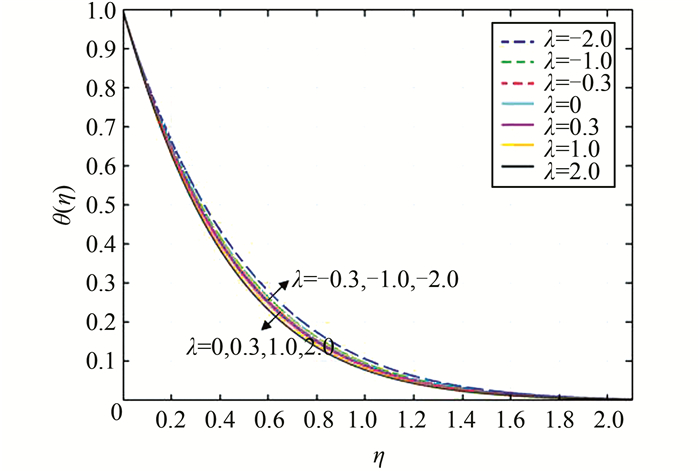
| 图 9 当Pr=1,ε=1时,对应不同λ的温度分布图 Figure 9 Temperature profiles for different values of λ when Pr=1 and ε=1 |
|
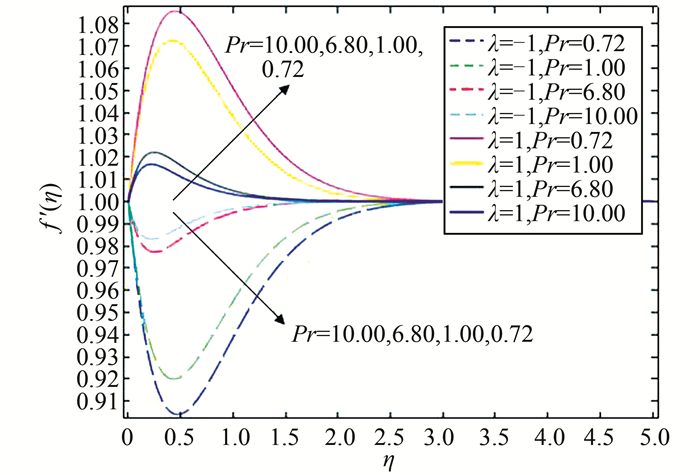
| 图 10 当λ=±1,ε=1时,对应不同Pr的速度分布图 Figure 10 Velocity profiles for different values of Pr when λ=±1 and ε=1 |
|
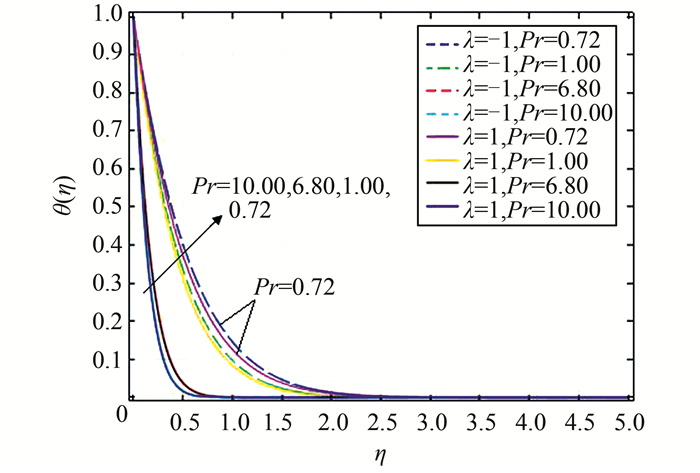
| 图 11 当λ=±1,ε=1时,对应不同Pr的温度分布图 Figure 11 Temperature profiles for different values of Pr when λ=±1 and ε=1 |
从表 1可看出,对于顺流(λ=1)和逆流(λ=-1),f″(0)几乎大小相等、方向相反,∣f″(0)∣都随Pr增大而减小.从表 2可得出,对于顺流和逆流,-θ′(0)都是正数,且值均随Pr增大而增大.
从图 2和图 4可得出,顺流时浮力参数越大,表面摩擦系数越大,而逆流时浮力参数越大,表面摩擦系数越小.这是因为顺流时浮力参数越大,速度越大,壁面剪切应力相应增大,从而使表面摩擦系数增大,而逆流正好相反.从图 4还可以看出,所有的曲线都在λ=0处相交,且f″(0)=0,这是因为此时方程(7)与温度无关,流场不受温度场影响;顺流时f″(0)随Pr数增大而减小(这与表 1的数据相符合),这是因为Pr数越大,粘度越大,流动速度越慢,表面剪切应力越小,从而使表面摩擦系数减小,逆流时正好相反.图 3显示-θ′(0)与浮力参数λ的关系与f″(0)类似,但对于给定的浮力参数,f″(0)与-θ′(0)随ε的变化方向相反.
图 5显示顺流时当Pr不变时,Nusselt数随λ缓慢增加,逆流时情况相反,因为顺流时浮力产生的压力梯度会使流动变快,从而加快表面热传递,而逆流会产生相反的压力梯度,使流动变慢,Nusselt数减小.从图 5还可以看出Nusselt数随Pr的增大而增大,因为Pr越大,粘度越大,导热系数越小,从而使-θ′(0)增大.
图 6~11给出ε、λ和Pr取不同值时的速度与温度分布图.从图 6可以看出,流体速度随ε的增大而增大,且ε越大,在壁面处速度梯度越小,与图 2相吻合;ε < 1与ε>1边界层方向相反;对于同样的ε,当ε < 1时顺流的边界层较薄,当ε>1时逆流的边界层较薄.
从图 8和图 10可以看出,对于顺流,速度先是增加,达到一定值后开始减小,最后达到稳定值,即跟外界速度趋于一致;浮力参数λ值越大,速度变化越明显.这是因为λ值越大,浮力越大,动能越大;流体流动时要克服阻力,因此速度降低,在无穷远处达到一个稳定值.逆流时速度变化趋势正好相反.
从图 7、图 9和图 11可以看出,不管是顺流还是逆流,对所有的ε、λ和Pr值,离壁面越远,温度越小,最后达到稳定值0.这是因为流体从壁面吸热,热能转化为其他形式的能,包括动能.从图 11可以看出,Pr越大,热边界层越薄,同时壁面温度梯度值越大(这与表 2数据一致),这是因为Pr大表示热扩散速率会比速度(动量)扩散速率要慢,热边界层厚度就会减小;Pr较小时,浮力对速度和温度分布的影响较明显.
3 结论本文从理论上研究不可压缩流体在垂直指数延伸壁面的驻点流和传热的相似解问题.借助于相似变换将偏微分方程组转换成非线性的常微分方程,然后利用COMSOL软件自带的PDE模块对模型进行仿真,详细分析了浮力参数λ和Prandtl数Pr对流体流动和传热特性的影响.
结果显示:顺流时,表面摩擦系数和Nusselt数均随浮力参数λ的增大而增大;随着Pr数增大,Nusselt数增大而表面摩擦系数减小.逆流时,表面摩擦系数和Nusselt数均随浮力参数λ的增大而减小,随Pr增大而增大.
本文所得结论便于深入了解该类问题的流动变化规律,在工程实际应用中可起到指导作用.
| [1] |
朱婧, 郑连存, 张欣欣. 具有延伸表面的驻点流动和传热问题的级数解[J].
应用数学和力学, 2009, 30(4): 432–442.
Zhu Jing, Zheng Liancun, Zhang Xinxin. Analytic solution of stagnation-point flow and heat transfer over a stretching sheet by means of homotopy analysis method[J]. Applied Mathematics and Mechanics, 2009, 30(4): 432–442. |
| [2] | Hiemenz K. Die grenzschicht in einem in dem gleichformingen flussigkeitsstrom eingetauchten gerade kreiszlinder[J]. Dingler's Polytechnic Journal, 1911, 326: 321–410. |
| [3] | Homann F. Die Einfluss grosse Zhigkeit bei der Strmung um der Zylinder und um die Kugel[J]. Zeitschrift für Angewandte Mathematik und Mechanik, 1936, 16(3): 153–164. DOI:10.1002/(ISSN)1521-4001 |
| [4] | Howarth L. On the solution of the laminar boundary layer equations[J]. Proceedings of the Royal Society of London, 1938, 164(919): 547–579. DOI:10.1098/rspa.1938.0037 |
| [5] | Layek G C, Mukhopadhyay S, Samad S A. Heat and mass transfer analysis for boundary layer stagnation-point flow towards a heated porous stretching sheet with heat absorption/generation and suction/blowing[J]. International Communications in Heat and Mass Transfer, 2007, 34(3): 347–356. DOI:10.1016/j.icheatmasstransfer.2006.11.011 |
| [6] | Bhattacharyya, Mukhopadhyay K S, Layek G C. Reactive solute transfer in magnetohydrodynamic boundary layer stagnation-point flow over a stretching sheet with suction/blowing[J]. Chemical Engineering Communications, 2012, 199(3): 368–383. DOI:10.1080/00986445.2011.592444 |
| [7] | Bhattacharyya K, Arif M G, Pramanik W A. MHD boundary layer stagnation-point flow and mass transfer over a permeable shrinking sheet with suction/blowing and chemical reaction[J]. Acta Technica, 2012, 57(1): 1–15. |
| [8] | Bhattacharyya K. Heat transfer in unsteady boundary layer stagnation-point flow towards a shrinking sheet[J]. Ain Shams Engineering Journal, 2013, 44(2): 259–264. |
| [9] | Fan Tao, Xu Hang, Pop I. Unsteady stagnation flow and heat transfer towards a shrinking sheet[J]. International Communications in Heat and Mass Transfer, 2010, 37: 1440–1446. DOI:10.1016/j.icheatmasstransfer.2010.08.002 |
| [10] | Xu Hang, Pop I, You Xiangcheng. Flow and heat transfer in a nano-liquid film over an unsteady stretching surface[J]. International Journal of Heat Transfer, 2013, 60: 646–652. DOI:10.1016/j.ijheatmasstransfer.2013.01.046 |
| [11] | Si Xinhui, Lin Lin, Zheng Liancun, et al. The exterior unsteady viscous flow and heat transfer due to porous expanding stretching cylinder[J]. Computers & Fluids, 2014, 105: 280–284. |
| [12] | Mustafa M, Hayat T, Pop I, Hendi A. Stagnation-point flow and heat transfer of a Casson fluid towards a stretching sheet[J]. Zeitschrift für Naturforschung A, 2012, 67(1-2): 70–76. |
| [13] | Prasad V R, Rao A S, Reddy N B, et al. Modelling laminar transport phenomena in a Casson rheological fluid from a horizontal circular cylinder with partial slip[J]. Archive Proceedings of the Institution of Mechanical Engineers. Part E: Journal of Process Mechanical Engineering, 2012, 227(4): 309–326. |
| [14] | Prasad V R, Vasu B, Bég O A, et al. Unsteady free convection heat and mass transfer in a Walters-B visco elastic flow past a semi-infinite vertical plate: a numerical study[J]. Thermal Sciences, 2011, 15(2): 291–305. |
| [15] | Makinde O D, Khan W A, Khan Z H. Buoyancy effects on MHD stagnation point flow and heat transfer of a nanofluid past a convectively heated stretching/shrinking sheet[J]. International Journal of Heat and Mass Transfer, 2013, 62(1): 526–533. |
| [16] | ISHAK. Mixed convection boundary layers in the stagnation-point flow toward a stretching vertical sheet[J]. Meccanica, 2006, 41: 509–518. DOI:10.1007/s11012-006-0009-4 |
| [17] | Chen Hui. Mixed convection unsteady stagnation-point flow towards a stretching sheet with slip effects[J]. Mathematical Problems in Engineering, 2014(1): 1–7. |
| [18] | Rahman M M, Roşca A V, Pop I. Boundary layer flow of a nanofluid past a permeable exponentially shrinking/stretching surface with second order slip using Buongiorno's model[J]. International Journal of Heat & Mass Transfer, 2014, 77: 1133–1143. |
 2018, Vol. 51
2018, Vol. 51




