文章信息
- 汪旭东, 孙伟翔, 许孝卓, 封海潮
- WANG Xudong, SUN Weixiang, XU Xiaozhuo, FENG Haichao
- 直驱多轿厢电梯系统的调度控制策略
- Research on scheduling control strategy of direct drive multi-car elevator system
- 武汉大学学报(工学版), 2019, 52(8): 716-721,728
- Engineering Journal of Wuhan University, 2019, 52(8): 716-721,728
- http://dx.doi.org/10.14188/j.1671-8844.2019-08-009
-
文章历史
- 收稿日期: 2018-11-12
随着经济的发展,高层建筑逐渐成为了现代化都市的标志.传统曳引式单井道电梯在服务于高层建筑时,由于电梯结构的限制,已经无法满足人们的需求.多轿厢电梯系统理论自从被提出以来,便受到了诸多学者的关注[1, 2].随着直线电机技术的不断发展,其应用在垂直提升系统结构上具有无配重、无牵引绳、无提升高度限制、可以实现多个轿厢运输等优点,所以将直线电机应用于高层建筑的垂直运输系统已然成为了一种新的趋势[3, 4].现阶段对多轿厢电梯系统的研究已经取得了不错的成果,文献[5]建立了一种多轿厢电梯的数学建模,文献[6]中提出了一种多轿厢电梯的结构,而对于多轿厢电梯系统的控制,诸多学者采用了如专家算法、动态分区算法、遗传编程算法等智能控制算法[7-12],且都取得了比较满意的效果.本文在直驱多轿厢电梯系统中引入了目的层预约的思想,并对轿厢间的碰撞进行了预防,通过利用电梯的服务完成时间评估控制系统的呼叫分配,最后,在不同的客流交通模式下对直驱多轿厢系统与传统单轿厢系统进行对比仿真,仿真结果表明,直驱多轿厢电梯群控系统相对于传统单轿厢系统具有更好的服务性能.
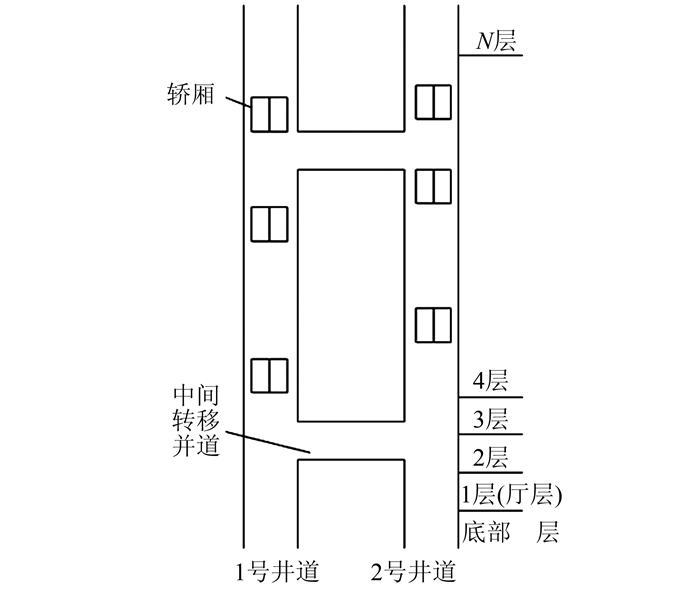
1 直驱多轿厢电梯群控系统的结构与传统单轿厢系统的结构不同,直驱多轿厢电梯系统摆脱了传统电机曳引绳的控制,是采用直线电机直接驱动的新型的电梯系统[13, 14],其在结构上提高了轿厢运行的自由度,为多轿厢的实现提供了可能.其中直驱多轿厢电梯系统的模型结构如图 1所示.
|
| 图 1 直驱多轿厢电梯系统的模型结构 Fig. 1 Structure of direct drive multi-car elevator system model |
通常乘客的客流交通模式有上、下行高峰交通模式、层间交通模式及空闲交通模式4类[15, 16].为了提高电梯群控系统的性能指标,在对乘客的客流交通模式识别后,系统通过不同的客流交通模式执行不同的运行策略.上、下行高峰交通模式时采用转移循环运行,为了提高系统的运行效率,设置成对运行井道及井道内相同的轿厢数目.轿厢实现转移必须是以避免碰撞干扰为前提,否则不转移.
在层间交通模式或空闲交通模式时,系统执行非转移运行,即在一个井道内多个轿厢可以独立上下运行.
2 多轿厢电梯群控系统的目的层预约传统电梯的呼梯结构由外召板及轿厢内部通讯板两部分组成,乘客完成呼梯需要输入2次信号.采用传统呼梯方式时,乘客的候梯时间、乘梯时间、轿厢分配等都是未知[17],针对传统呼梯方式的不足,在直驱多轿厢电梯群控系统中引入目的层预约的思想.其中,目的层预约的直驱多轿厢电梯群控系统的控制结构如图 2所示.

|
| 图 2 多轿厢电梯群控系统的控制结构 Fig. 2 Control structure of multi-car elevator group control system |
直驱多轿厢电梯群控系统目的层预约的特点是把传统单梯的上下行方向按钮改换成一个数字化的登记面板,如图 3所示,乘客呼梯只需要在门厅位置的登记面板上输入所要到达楼层的信息,然后系统会将乘客的交通信息通过群控制模块、轿厢控制模块之间的信息交流合作对门厅的呼叫登记进行应答并做出最优的呼叫分配, 对于系统所分配的结果将会直接通过指引部分显示在登记面板上.
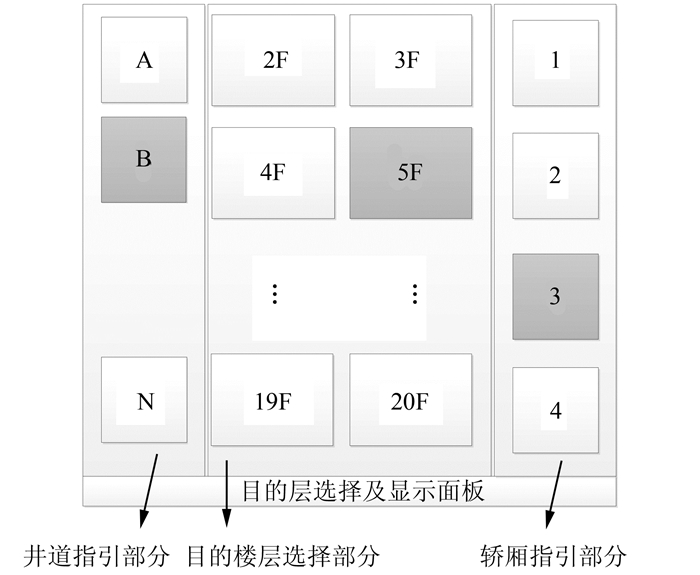
|
| 图 3 数字化的登记面板 Fig. 3 Digital registration panel |
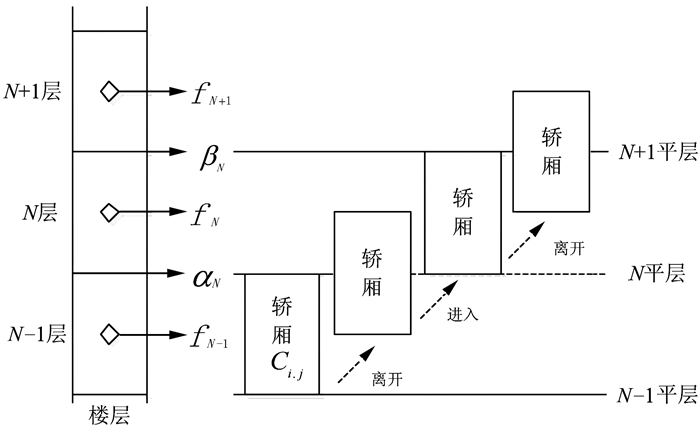
直驱多轿厢电梯的群控系统在执行呼叫分配期间,由于乘客的目的层已经预约登记,系统对乘客所要去的楼层已经做到提前识别,所以在一定程度上系统的派梯已经减少了部分碰撞干扰.为了更好地防止轿厢在运行过程的碰撞发生可能,对系统中轿厢的检测约束必不可少.其中,如果相邻2个轿厢的位置处在了同一个楼层,则默认此时必然会发生碰撞,即防止碰撞发生的其中一种有效的方法就是在同一时刻避免相邻轿厢处于同一楼层.具体的检测预防过程是:将井道所处的每个楼层都分为2个半层状态,设轿厢高度与一个楼层高度一致,其中举例轿厢在井道中的上行运行状态,如图 4所示.
|
| 图 4 轿厢上行运行状态 Fig. 4 Car running state |
图 4中所描述的过程是轿厢从建筑N-1层离开进入N层(N表示楼层数),接着从N层离开即将进入N+1层.其中,αN为建筑第N层的下底边,βN为建筑第N层的上顶部边;fN为建筑第N层的中心高度,fN-1、fN+1分别为建筑第N-1、N+1层的中心高度.设λi, j为轿厢Ci, j(i表示轿厢号,j表示井道号)的形心高度,则对于轿厢Ci, j自N-1层离开进入N层的过程用建筑楼层及轿厢形心高度的物理量可以表示为:fN-1<λi, j<fN;当λi, j=fN时,表示轿厢Ci, j完全处于第N层;当fN<λi, j<fN+1时,则表示为轿厢Ci, j离开N层即将进入N+1层的过程.
所以在某一个时间步长τ,如果一个竖直井道中的2个轿厢所处的楼层位置相同,则两轿厢必然会发生碰撞.根据轿厢的运行状态轨迹对所有轿厢的行驶位置进行实时监测,为保证相邻2个轿厢之间不发生碰撞,需要确保相邻轿厢间的距离至少保持一个楼层的长度,即|βN-αN|.定义λi, jτ为轿厢Ci, j在时间步长τ时所对应的形心高度,则预防相邻2个轿厢发生碰撞需要满足下式约束:
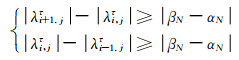 (1)
(1)
对直驱多轿厢电梯系统进行群控设计,首先需要满足之前叙述的避免碰撞发生条件.在直驱多轿厢电梯群控系统中,系统从满足防止碰撞发生条件的候选轿厢集合中选择并分配1台最为合适的轿厢去响应乘客呼叫,为了使乘客在登记过目的楼层系统产生呼叫后的候梯时间最小,群控系统需要计算所有候选电梯轿厢去响应呼叫所需要的时间,并从中选择1台使乘客候梯时间最短的轿厢去执行呼叫.群控系统的选择基于第k号轿厢Ck.j的评估值evlk,可以根据以下表达式计算具有最小评估值的轿厢Ck.j的门厅呼叫:
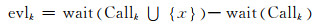 (2)
(2)
式中:Callk是1组已经分配给轿厢Ck.j但尚未提供服务的厅层呼叫;wait(Callk)是轿厢Ck.j的总的估计候梯时间;x是即将准备分配给Ck.j的门厅呼叫.当呼叫x被分配给Ck.j时,评估值evlk会显示Ck.j的总的估计等待时间将延迟,当然,如果evlk足够的小,那么x到Ck.j的分配对Ck.j的等待时间将几乎没有影响.
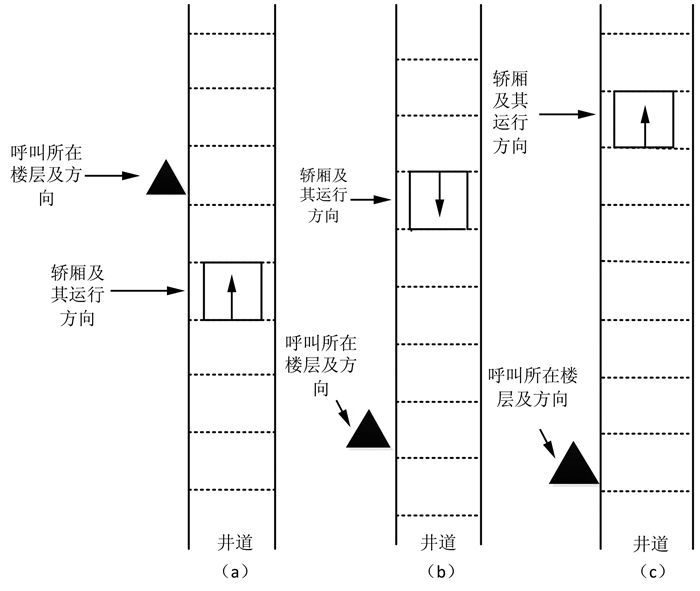
对于轿厢总的估计等待时间wait(Callk)将会因为乘客呼叫申请的方向与电梯轿厢当前运行方向的不同而存在3种可能发生的类型,如图 5所示.
|
| 图 5 3种不同类型的呼叫运行方向 Fig. 5 Three different types of call directions |
1) 乘客的呼叫申请方向与轿厢当前运行方向一致,具体运行如图 5(a)所示,则有
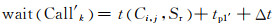 (3)
(3)
式中:t(Ci, j, Sr)为轿厢Ci, j在当前状态到达乘客呼叫层Sr所用运行时间;tp1′为轿厢Ci, j在当前状态到达乘客呼叫层Sr期间为躲避碰撞进行延迟或者停靠所消耗的时间;Δt为轿厢Ci, j从当前运行1号井道的转移楼层处转移到成对存在的2号井道的转移楼层所需要的时间(如果客流交通为非高峰交通模式时或者轿厢并不满足转移条件,则该时间不存在),其中Δt又可以表示为
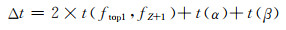 (4)
(4)
式中:t(ftop1, fZ+1)表示轿厢Ci, j从1号井道的转移楼层到完全进入转移机构所用的时间,此处设定轿厢进入转移机构与离开转移机构所用时间相同;t(α)表示轿厢Ci, j转移机构实现转移过程的总耗时间;t(β)表示轿厢Ci, j在转移楼层处等待进入转移机构所耗的时间(由于转移机构在运送一个轿厢后会立刻恢复原有状态,所以一般情况下,转移机构恢复时间可以忽略不计).
2) 乘客的呼叫申请方向与轿厢当前运行方向相反,如图 5(b)所示,则有
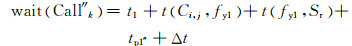 (5)
(5)
式中:t(Ci, j, fy1)为轿厢Ci, j从当前状态运行到该方向下的最远楼层fy1所用时间;t(fy1, Sr)为轿厢从最远楼层fy1到呼叫层Sr所用时间;t1为状态1下,乘客的呼叫申请时间(时间过小时可以忽略不计);tp1″为该状况下,轿厢运行期间转向以及为躲避碰撞进行延迟或者停靠所消耗的时间.
3) 乘客的呼叫申请方向与轿厢当前运行方向一致,但是呼叫楼层位于轿厢运行的后侧,具体运行如图 5(c)所示,则有
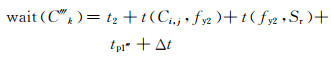 (6)
(6)
式中:t2 为状态2下,乘客的呼叫申请时间;fy2为轿 厢Ci,j当前运行方向所达的最远楼层;tp1″为该状况下,轿厢运行期间转向以及为躲避碰撞进行延迟或 者停靠所消耗的时间.
根据直驱多轿厢电梯系统的调度策略可知,轿厢一旦到达呼叫层乘客进入轿厢开始响应服务召唤,之后轿厢的运行便不存在转移,即服务是在一个竖直井道中完成的,则一个轿厢Ci, j从乘客起始呼叫层Sr到服务目的楼层dr所用的平均乘梯时间可以表示为
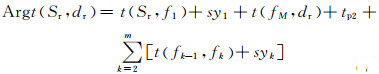 (7)
(7)
式中:fk∈Fi, j,Fi, j为轿厢Ci, j到达所需服务的目的楼层dr中间所有会停靠楼层的集合(不含目的楼层dr); m为集合的元素个数;t(Sr, f1)为轿厢Ci, j从乘客呼叫层Sr到达第1个停靠处f1所运行的时间;syk为轿厢Ci, j在到达目的层dr中途所经过的停靠层所停留的时间(不包括轿厢可能在运行期间为避免碰撞发生而延迟或者停靠的时间),syk即包括乘客进入及离开轿厢所需的时间tb、轿厢Ci, j开、关门所需时间tc,可表示syk=tb+tc;t(fk-1, fk)为轿厢Ci, j从停靠层fk-1去往下一处停靠层fk所需运行的时间;t(fM, dr)为轿厢Ci, j自第M个停靠楼层fM到达目的楼层dr所需运行时间;tp2为轿厢Ci, j运行期间避免碰撞延迟或停靠所耗费的时间.
综上,轿厢Ci, j的平均服务完成时间可以表示为
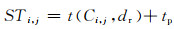 (8)
(8)
式中:t(Ci, j, dr)为轿厢Ci, j从当前状态位置运行到目的层dr的所用时间;tp为轿厢运行期间躲避碰撞而延迟或停靠的时间,此时tp只考虑了在乘客呼叫层Sr和乘客所要到达的目的层dr处的避碰延迟或者停靠时间:
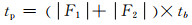 (9)
(9)
式中:|F1|={fk∈F′i+1.j, k < dr}为轿厢Ci+1.j在超过目的层之前所有需要停靠的楼层集合;F′i, j⊂Fi, j为到达目的层前计划停靠的总的楼层集合;|F2|={fk∈F′i-1.j, k>dr}表示轿厢Ci-1.j在超过目的层之前所有需要停靠的楼层集合;tb为在一个楼层轿厢停靠或者延迟所需要的时间.
进而,对于最优轿厢的选择有
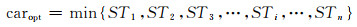 (10)
(10)
依据上式选择平均服务完成时间最小的那个轿厢去执行呼叫,其中n表示为候选轿厢的个数,STn表示为第n个轿厢的平均服务完成时间.
5 系统仿真分析对直驱多轿厢电梯群控系统进行计算机仿真,其中系统的仿真参数设置如表 1所示.
| 物理量 | 参数 |
| 楼层数/层 | 20 |
| 每层楼高/m | 4 |
| 轿厢最大承载量/人 | 20 |
| 轿厢高度/m | 4 |
| 轿厢运行加速度/(m·s-2) | 2 |
| 轿厢运行最大速度/(m·s-1) | 6 |
| 轿厢开门时间/s | 1.8 |
| 轿厢关门时间/s | 2.4 |
| 上、下乘客时间/s | 1.8 |
| 井道数目 | 2 |
| 仿真时间/min | 5 |
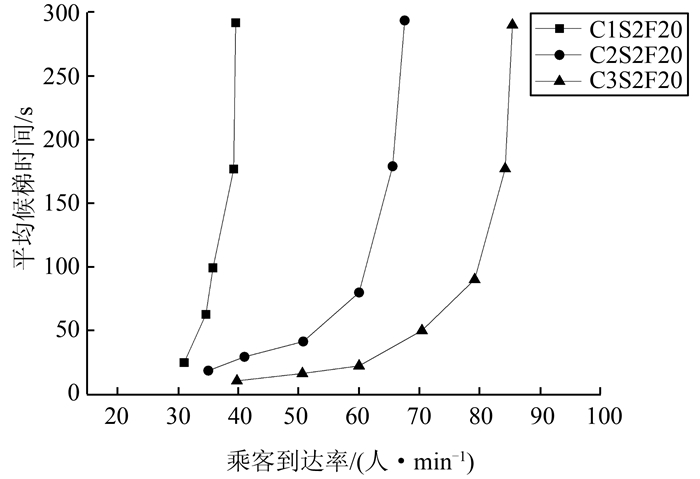
本文使用Java语言在集成开发环境Eclipse中编制仿真程序,构建直驱多轿厢电梯系统的仿真环境,在仿真环境中,分别在上、下行高峰交通模式、空闲交通模式及层间交通模式这4种交通情况下选择不同的轿厢数(CxSyFz表示x个轿厢y个井道z层楼),对直驱多轿厢电梯群控系统与传统单轿厢系统在乘客到达率0~100人/min情况下进行对比仿真,为了获得准确的结果,以多次运行的评价指标求取的平均值作为最终的评价指标数据.其中乘客的评价候梯时间结果如图 6~9所示.
|
| 图 6 上行高峰交通模式 Fig. 6 Upstream peak traffic patternc |
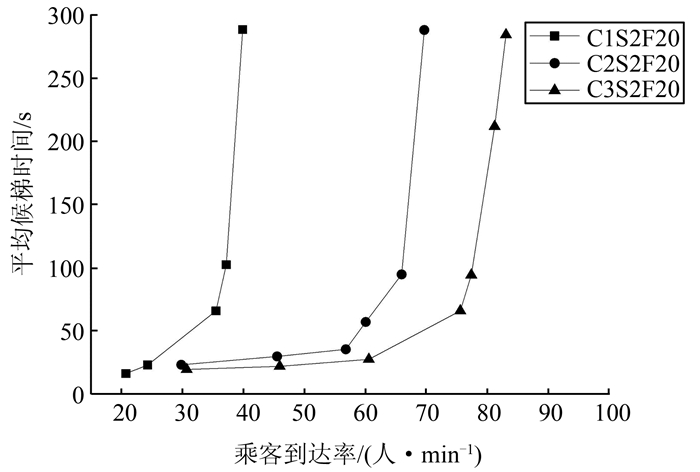
|
| 图 7 下行高峰交通模式 Fig. 7 Downstream peak traffic pattern |
|
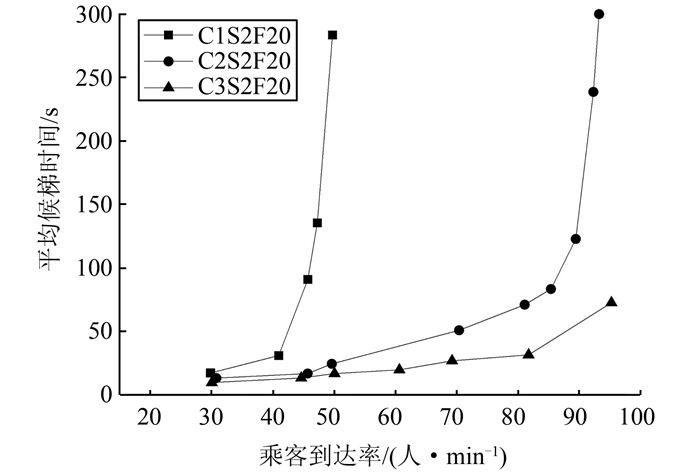
| 图 8 层间交通模式 Fig. 8 Interlayer traffic pattern |
|
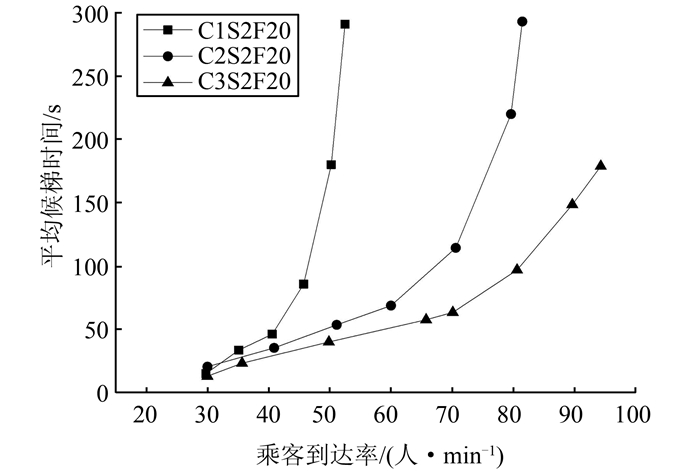
| 图 9 空闲交通模式 Fig. 9 Idle traffic pattern |
从4种不同的客流交通模式的对比仿真结果可以看出,在相同的仿真环境中,随着系统投入的轿厢数目的增加,在相同乘客的平均候梯时间条件下乘客的到达人数就越多.并且可以清晰地看出乘客到达率在30~70人/min时系统的性能相对平稳.与传统单轿厢系统相比,直驱多轿厢电梯群控系统在减小乘客候梯时间的性能方面具有绝对的优势.
6 结论本文针对传统单轿厢系统在服务高层建筑中的不足,提出了直驱多轿厢电梯群控系统并进行研究,为了获得优良的电梯系统性能,在多轿厢电梯系统中引入了目的层预约的思想,并对在运行过程中轿厢间可能发生的碰撞进行了预防,通过采用服务完成时间的评估方法对电梯群控系统进行控制,最后对直驱多轿厢电梯群控系统与传统单轿厢系统进行对比仿真,结果分析表明,在电梯系统的服务性能方面,目的层预约的直驱多轿厢电梯系统在4种不同的客流交通模式下相比于传统单轿厢系统具有更小的乘客候梯时间, 该研究结果证明了直驱多轿厢电梯系统的综合运行性能的可行性,具有很强的实际研究价值.
| [1] |
Sandor Markon, Yasuhiro Komatsu, Akitomo Yamanaka, et al. Linear motor coils as brake actuators for multi-car elevators[C]//Proceedings of International Conference on Electrical Machines and Systems. Seoul, Korea, 2007: 1492-1495.
|
| [2] |
Shunya Ishimaru, Shingo Yamaguhi. A simplified mathematical modeling and zone scheduling for multi-directional multi-car elevators[C]// IEEE 4th Global Conference on Consumer Electronics (GCCE), 2015: 61-64.
|
| [3] |
袁世鹰, 焦留成, 朱建铭. 直线同步电动机提升系统的研究现状及展望[J]. 焦作工学院学报, 1998(2): 45-49. Yuan Shiying, Jiao Liucheng, Zhu Jianming. Research status and prospect of linear synchronous motor lifting system[J]. Journal of Jiaozuo Institute of Technology, 1998(2): 45-49. |
| [4] |
汪旭东, 袁世鹰, 焦留成, 等. 永磁直线同步电动机垂直运输系统的研究现状[J]. 微电机, 2000(5): 35-38. Wang Xudong, Yuan Shiying, Jiao Liucheng, et al. Principle and present study situation of permanent magnet linear synchronous motor for vertical transportation system[J]. Micro-motor, 2000(5): 35-38. DOI:10.3969/j.issn.1001-6848.2000.05.012 |
| [5] |
Ishimaru S, Yamaguchi S. Proposal and evaluation of a state transition model of multi-car single-shaft elevators[C]// IEEE 3rd Global Conference on Consumer Electronics (GCCE), 2014: 584-587.
|
| [6] |
钟武杰.一种多轿厢循环电梯[P]. 200920225007.8. 2010-05-19. Zhong Wujie. A Multi-car Circulation Elevator[P]. 200920225007.8. 2010-05-19. |
| [7] |
Lu Yu, Shingo Mabu, Zhang Tiantian, et al. Multi-car elevator group supervisory control system using genetic network programming[C]// IEEE Congress on Evolutionary Computation (CEC), 2009: 2188-2193.
|
| [8] |
Hiroki Ishihara, Shohei Kato. The effectiveness of dynamic zoning in multi-car elevator control[C]// IEEE 3rd Global Conference on Consumer Electronics (GCCE), 2014: 601-604.
|
| [9] |
Satoshi Takhashi, Hajime Kita, Hiromichi Suzuki, et al. Simulation-based optimization of a controller for multi-car elevators using a genetic algorithm for noisy fitness function[C]// IEEE Congress on Evolutionary Computation (CEC), 2003: 1582-1587.
|
| [10] |
Hiroki Ishihara, Shohei Kato. Multi-car elevator control using dynamic zoning[C]// IEEE 2nd Global Conference on Consumer Electronics (GCCE), 2013: 546-549.
|
| [11] |
Takeshi F, Shohei U, Ayaka K, et al. Algorithm for controlling multi-car elevator systems based on procedures estimating efficiency of passenger transport and call assign ability[J]. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 2009, E92-A(11): 2790-2793. DOI:10.1587/transfun.E92.A.2790 |
| [12] |
Miyamoto T, Yamaguchi S. MCESIM: A multi-car elevator simulator[J]. IECIE Trans.Fundam, 2008, E91-A(11): 3207-3214. DOI:10.1093/ietfec/e91-a.11.3207 |
| [13] |
汪旭东, 许孝卓, 封海潮, 等.一种直驱循环多轿厢电梯及其循环系统[P].ZL200910064738.3.2011-12-25. Wang Xudong, Xu Xiaozhuo, Feng Haichao, et al. A Cordless Recycling Multi-Car Elevator and its Circulation System[P]. ZL200910064738.3.2011-12-25. |
| [14] |
马海霞, 李中兴, 刘英杰, 等. 曳引式电梯节能检测方法及装置研究[J]. 科学技术与工程, 2016, 32(16): 247-250. Ma Haixia, Li Zhongxing, Liu Yingjie, et al. Study on energy testing method and device of traction elevator[J]. Science Technology and Engineering, 2016, 32(16): 247-250. |
| [15] |
秦臻, 赵建勇, 严义. 基于多值分类SVM的电梯交通模式识[J]. 计算机工程, 2011, 37(9): 201-206. Qin Zhen, Zhao Jianyong, Yan Yi. Pattern recognition of elevator traffic mode based on multi-value classification support vector machine[J]. Computer Engineering, 2011, 37(9): 201-206. DOI:10.3969/j.issn.1000-3428.2011.09.070 |
| [16] |
熊新国, 田红彬. 电梯群控系统交通模式识别[J]. 制造业自动化, 2010, 32(11): 49-51. Xiong Xinguo, Tian Hongbin. Traffic pattern recognition of elevator group control system[J]. Manufacturing Automation, 2010, 32(11): 49-51. DOI:10.3969/j.issn.1009-0134.2010.11.16 |
| [17] |
付丽君, 周崇. 电梯群控系统的最优调度仿真[J]. 计算机仿真, 2012, 29(4): 262-267. Fu Lijun, Zhou Chong. Optimal dispatch control simulation of elevator group control system[J]. Computer Simulation, 2012, 29(4): 262-267. |
 2019, Vol. 52
2019, Vol. 52



