文章信息
- 万宇豪, 何蕴龙
- WAN Yuhao, HE Yunlong
- 黄金坪坝基防渗墙地震反应规律
- Seismic response law of cutoff wall of Huangjinping rockfill dam
- 武汉大学学报(工学版), 2016, 49(3): 378-383
- Engineering Journal of Wuhan University, 2016, 49(3): 378-383
- http://dx.doi.org/10.14188/j.1671-8844.2016-03-010
-
文章历史
- 收稿日期: 2015-10-15
混凝土防渗墙常用作深厚覆盖层上土石坝坝基的垂直防渗设施[1].由于夹持在较柔性的砂砾石地基中,深而薄的刚性防渗墙主要受到上覆坝体压力、水压力以及覆盖层与防渗墙之间的不均匀沉降引起的负摩擦阻力等作用[1],一旦遭遇地震作用,应力变形状况将更加复杂.目前国内外对防渗墙的研究主要集中在静力工况,且大部分防渗墙的深度都不超过100 m,对建在深厚覆盖层上的土石坝坝基防渗墙的应力变形状态研究较少,对地震作用下防渗墙的应力变形分析及其抗震安全性等问题认识程度有限[2].本文以黄金坪沥青混凝土心墙坝坝基防渗墙为工程背景,采用时程法对坝基防渗墙进行了动力分析,并且对地震过程中防渗墙的应力分布机制进行了研究.
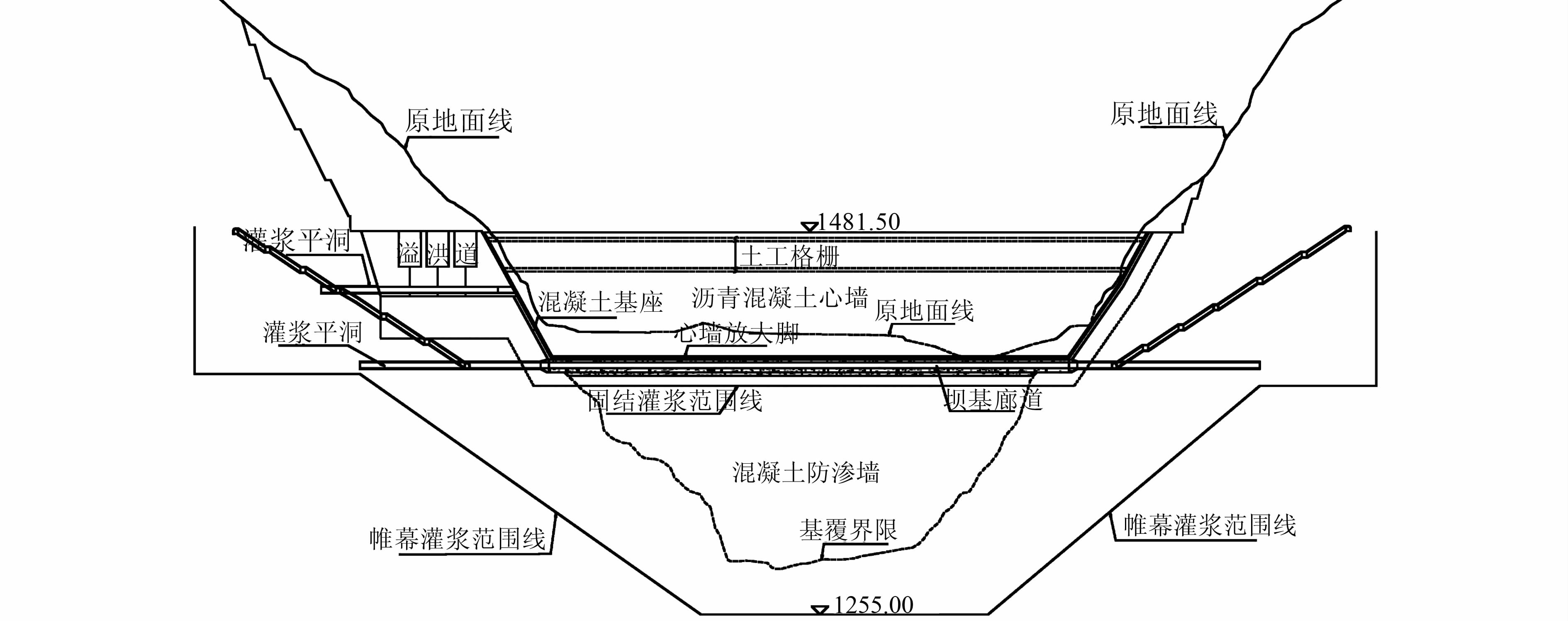
1 工程概况黄金坪沥青混凝土心墙堆石坝最大坝高85.5 m,图 1为大坝典型纵剖面图,图 2为大坝典型横剖面图.坝址区河床覆盖层深厚,最大厚度达133.92 m[2].坝基覆盖层采用厚度为1.2 m的混凝土防渗墙全封闭防渗,防渗墙最大深度为113.8 m,沿纵向最大宽度达280 m[2].地震动峰值加速度为2.2 m/s2,设计地震烈度为8度[2].
|
| 图 1 大坝典型纵剖面图(单位:m) Figure 1 Typical longitudinal profile of dam(unit:m) |
|
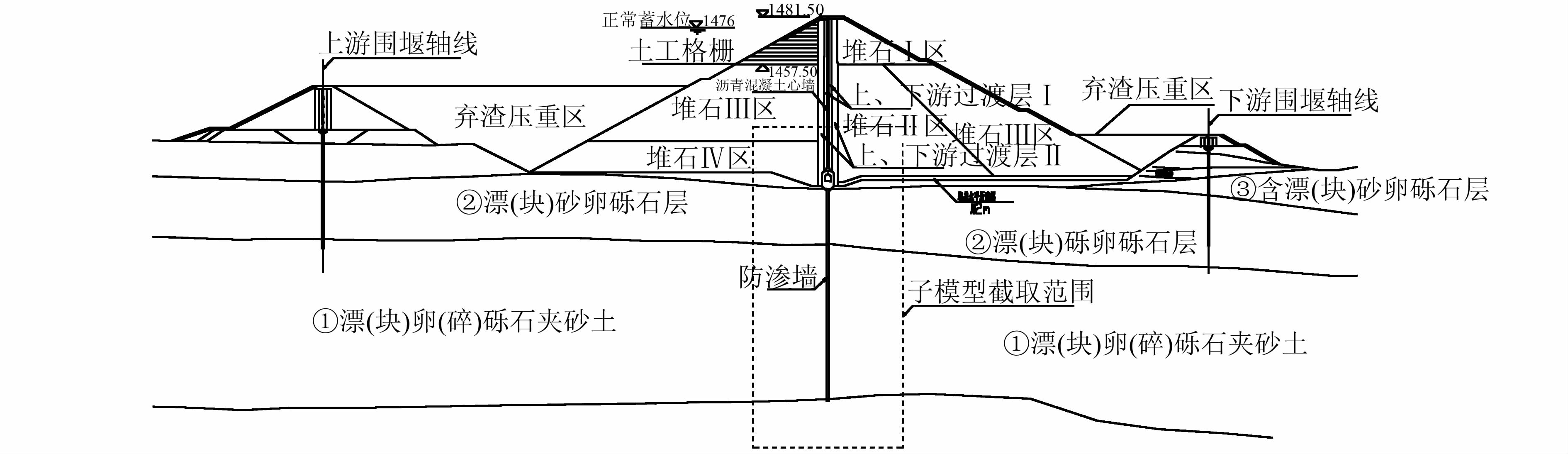
| 图 2 大坝典型横剖面图(单位:m) Figure 2 Typical transverse profile of dam(unit:m) |
防渗墙在施工过程中形成的泥皮、残渣等对防渗墙的受力特性有较大影响,在计算过程中需进行较为精细的模拟,因此,本文在坝基防渗系统部位采用子模型技术[3~7],对所关心的一些细部结构划分较为细致的网格,在整体模型计算的基础上进行二次分析,获得更加准确的结果.
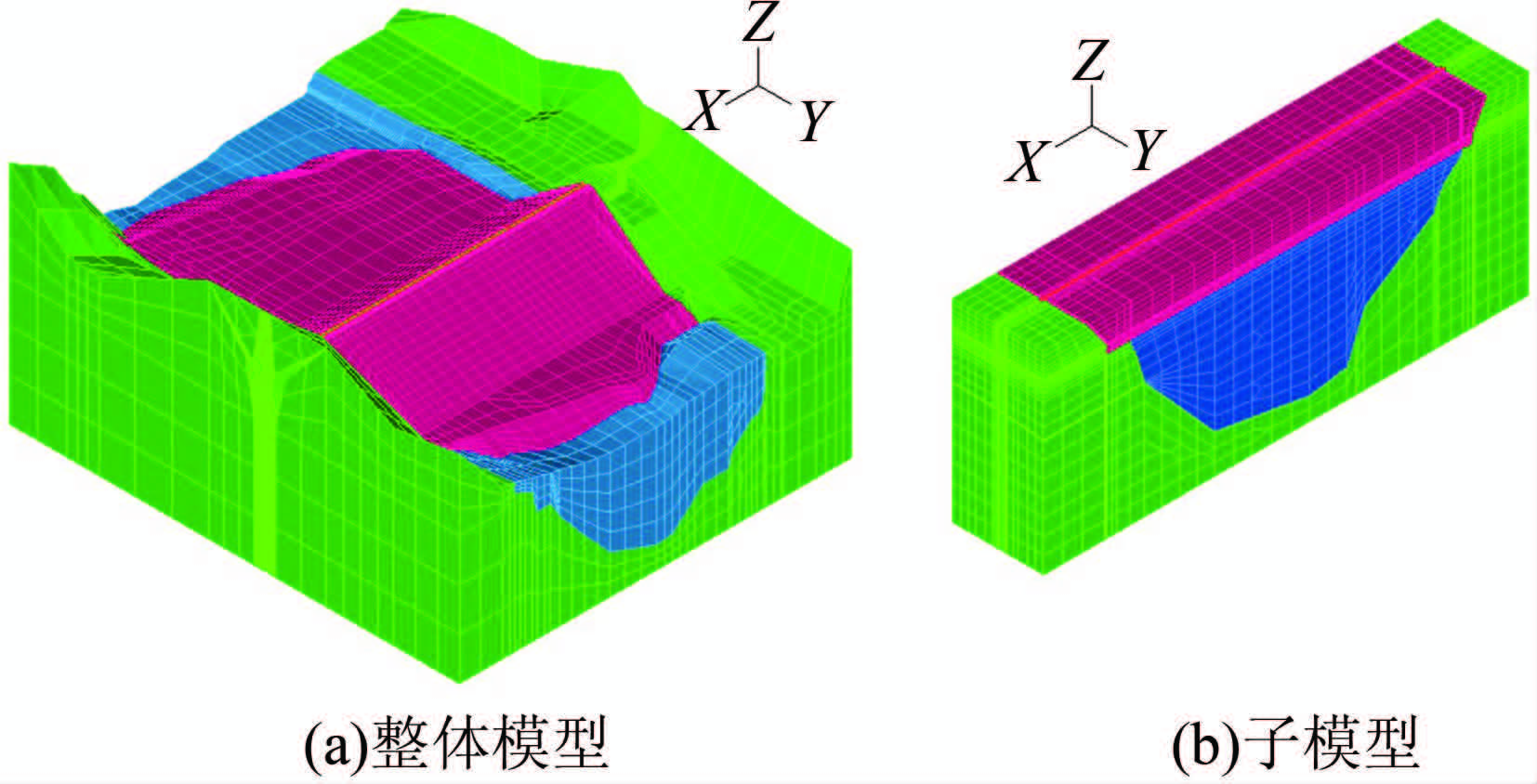
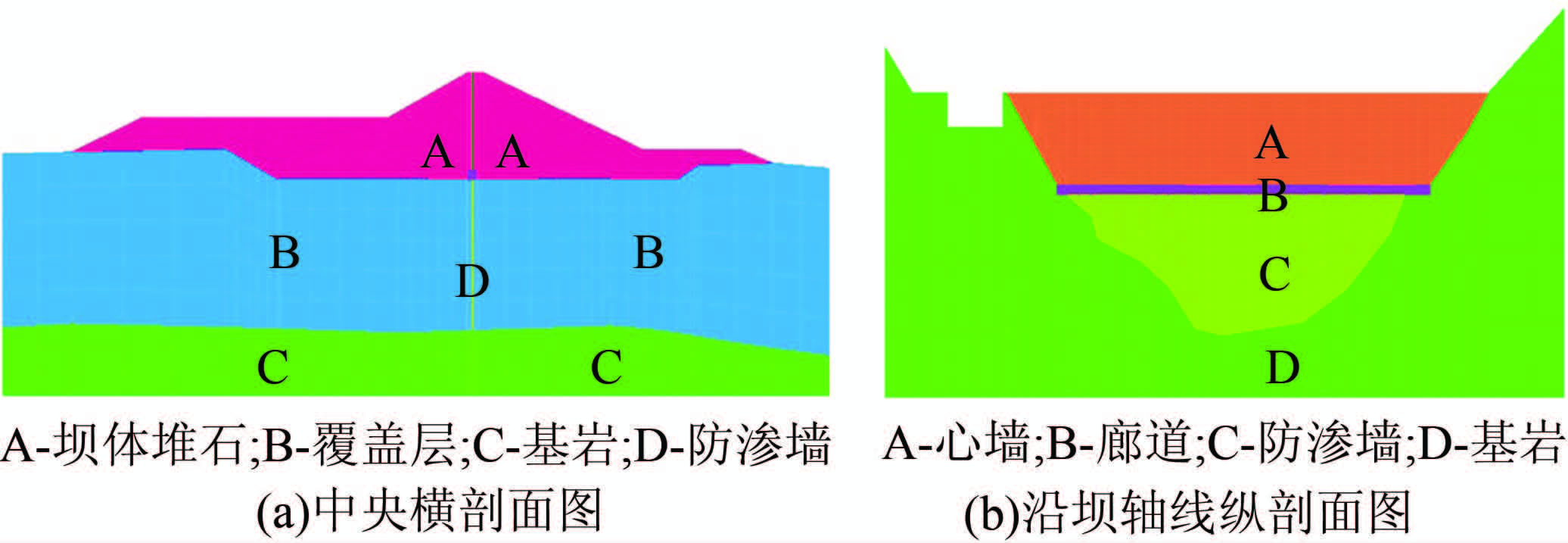
图 3为黄金坪大坝有限元整体模型和子模型.有限元整体模型规模为36 899个结点、35 183个单元.子模型共有45 854个结点、44 974个单元.根据圣维南原理,实际荷载被等效荷载替代后,应力和应变只是在荷载施加的位置附近有所改变,这说明只有在荷载集中的位置才有应力集中效应,如果子模型的位置远离应力集中的位置,则子模型内部就能得到较精确的结果[2].子模型的切割边界范围见图 2.在计算模型中,防渗墙上下游侧泥皮以及墙底残渣等各类接触面采用有厚度节理单元[8~11]进行模拟.图 4为整体模型剖面图.
|
| 图 3 有限元模型 Figure 3 FEM mesh model |
|
| 图 4 整体模型剖面图 Figure 4 Profile of complete model |
动力计算采用人工生成的规范波,人工波生成时,迭代误差取为5%,其中特征周期Tg按照场地类别取0.3 s,反应谱最大值的代表值βmax取为1.6,设计加速度代表值为0.22g[2].通过SHAKE91程序反演后,坝基水平向基岩地震波峰值为0.120g,竖直向基岩地震波峰值为0.098g,横河向、顺河向和竖直向输入加速度之比为3∶3∶2,计算地震时长20 s,时间步长为0.02 s,各方向地震波时程如图 5所示[2].

|
| 图 5 坝址区基岩地震加速度时程曲线 Figure 5 Acceleration time history curves of earthquake |
在计算中,混凝土和基岩采用线弹性本构模型,其材料参数见表 1.动力计算中的弹性模量在静力弹性模量的基础上提高30%.坝体材料及覆盖层的静力本构为Duncan-Chang E-μ模型[12~13],其材料参数见表 2;动力本构关系采用Hardin-Drnevich模型[14~16],其材料参数见表 3;有厚度节理单元参数见表 4.
| 材料类型 | ρd/(t·m-3) | E/GPa | μ |
| 防渗墙混凝土 | 2.40 | 32.5 | 0.167 |
| 廊道混凝土 | 2.40 | 30.0 | 0.167 |
| 基岩 | - | 10 | 0.25 |
| 材料类型 | 干密度ρd/(g·cm-3) | 非线性强度 | φ0/(°) | C/kPa | K | n | Rf | D | G | F | |
| φ0/(°) | Δφ/(°) | ||||||||||
| 沥青混凝土 | 2.425 | — | — | 34.8 | 320 | 290 | 0.02 | 0.66 | 0 | 0.47 | 0 |
| 过渡层Ⅰ | 2.300 | 51.6 | 8.4 | 39.2 | 172 | 1115 | 0.35 | 0.66 | 7.8 | 0.30 | 0.083 |
| 过渡层Ⅱ | 2.320 | 49.2 | 6.5 | 38.2 | 185 | 1208 | 0.37 | 0.77 | 8.9 | 0.29 | 0.113 |
| 堆石Ⅳ | 2.190 | 51.9 | 8.9 | 38.3 | 217 | 1003 | 0.37 | 0.78 | 6.3 | 0.31 | 0.137 |
| 堆石Ⅰ、Ⅱ | 2.200 | 49.7 | 5.8 | 40.4 | 158 | 1037 | 0.31 | 0.76 | 5.9 | 0.30 | 0.114 |
| 堆石Ⅲ | 2.190 | 48.8 | 5.9 | 39.5 | 170 | 976 | 0.34 | 0.80 | 6.2 | 0.28 | 0.121 |
| 覆盖层① | 2.210 | — | — | 32.0 | 10 | 1200 | 0.25 | 0.80 | 5.0 | 0.35 | 0.160 |
| 覆盖层② | 2.230 | — | — | 30.0 | 10 | 1100 | 0.23 | 0.81 | 5.7 | 0.38 | 0.163 |
| 覆盖层③ | 2.260 | — | — | 30.0 | 10 | 1150 | 0.24 | 0.83 | 6.2 | 0.37 | 0.151 |
| 围堰堆石 | 2.210 | 48.5 | 6.2 | 38.7 | 164 | 948 | 0.37 | 0.76 | 7.7 | 0.28 | 0.128 |
| 材料类型 | K | n | λmax | μ | γr |
| 沥青混凝土 | 2 000 | 0.200 | 0.28 | 0.3 | 0.000 8 |
| 过渡料 | 2 920 | 0.452 | 0.26 | 0.3 | 0.000 3 |
| 堆石料 | 3 100 | 0.468 | 0.24 | 0.3 | 0.000 1 |
| 覆盖层 | 2 260 | 0.504 | 0.24 | 0.3 | 0.000 1 |
| 围堰堆石 | 3 100 | 0.468 | 0.24 | 0.3 | 0.000 1 |
| 项 目 | φ/(°) | C/kPa | Rf | Ksi | n | Kni /(MPa·m-1) |
| 泥皮 | 11 | 10.5 | 0.89 | 757 | 0.80 | 300 |
| 残渣单元 | 41 | 0 | 0.84 | 2 500 | 0.76 | 400 |
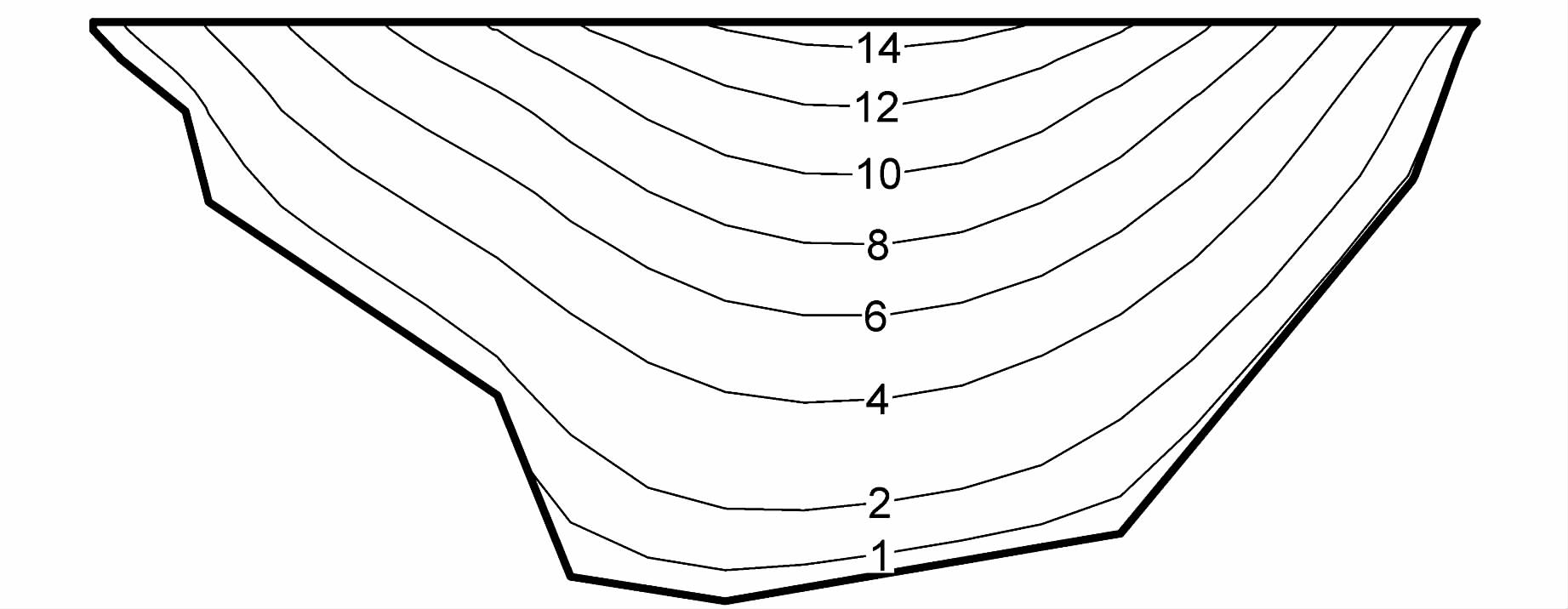
图 6为防渗墙中央纵剖面顺河向加速度包络图.从图中可以看出:顺河向加速度在河床中央明显大于两岸侧,且随着高程的增加而增大,最大值出现在墙顶中部,为3.05 m/s2.图 7为防渗墙中央纵剖面顺河向动位移包络图.从图中可以看出:顺河向动位移的分布规律表现为由两岸向河床中央逐渐增大,且随着高程的增加而增大,最大值出现在墙顶中部,为15.1 mm.地震作用下的防渗墙顺河向动位移分布规律与静力工况下的顺河向位移相似,但远小于静位移,静力工况下的最值为32.6 cm(顺河向),在地震过程中,总位移为34.11 cm,相对于静力工况增加了4.6%.
|
| 图 6 防渗墙顺河向加速度包络图 (左侧为左岸,单位:m/s2) Figure 6 Horizontal acceleration envelope diagram of cutoff wall (left side is left bank,unit:m/s2) |
|
| 图 7 防渗墙顺河向动位移包络图 (左侧为左岸,单位:mm) Figure 7 Horizontal dynamic displacement envelope diagram of cutoff wall(left side is left bank,unit:mm) |
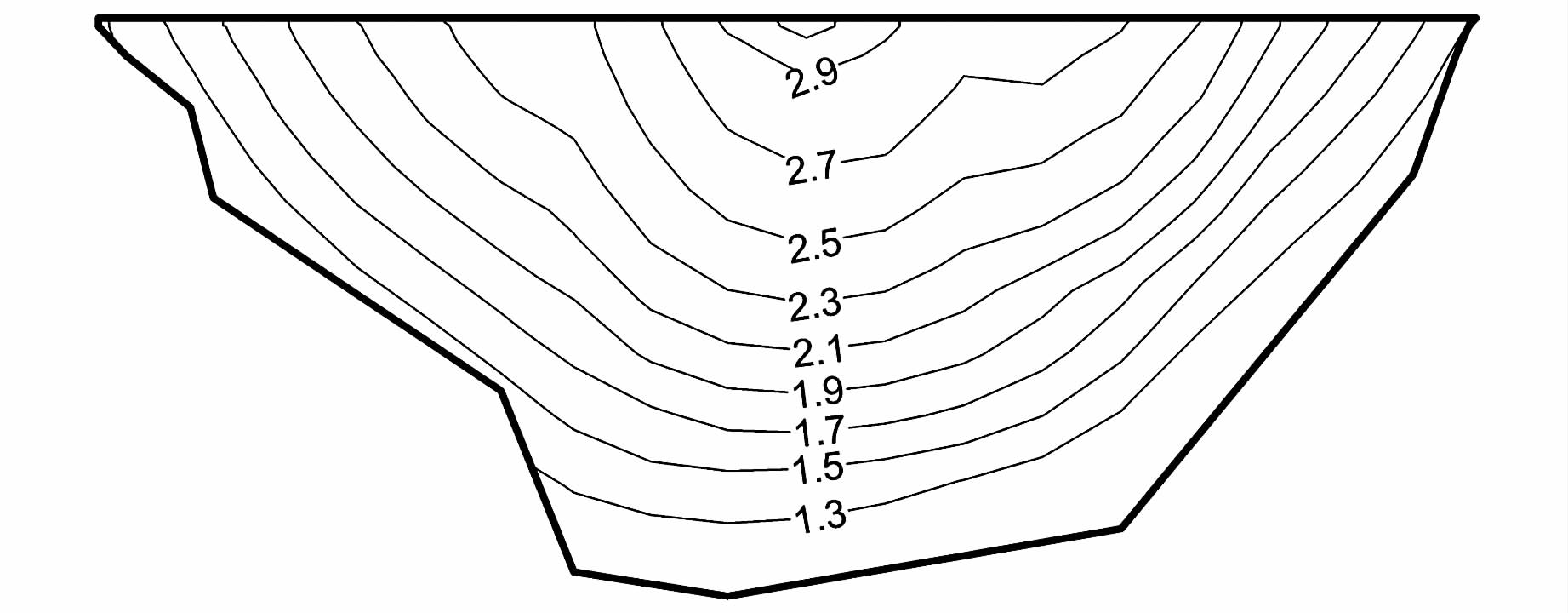
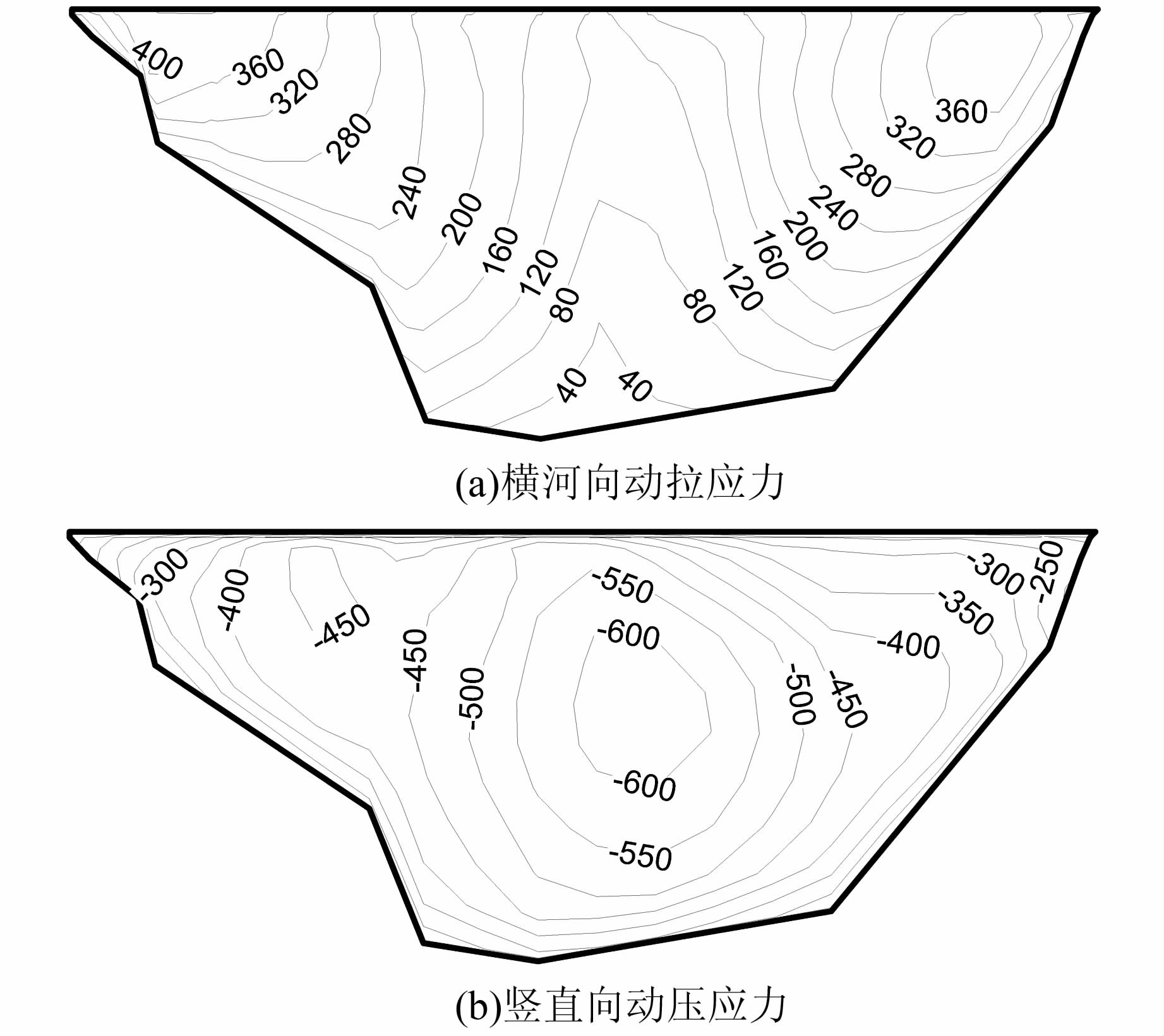
图 8为防渗墙中央纵剖面横河向和竖直向动应力包络图.在本文中,应力以受拉为正,受压为负.从图中可以看出:在地震作用下,防渗墙中央纵剖面横河向动拉应力由河床中央向两岸侧逐渐增大,并基本沿河床中央呈对称分布,最大值出现在左岸靠近墙顶的折坡附近,为405 kPa;在竖直向,墙身中部动压应力较大,并由河床中央向两岸侧逐渐减小,最大动压应力为-630 kPa,出现在防渗墙中部约1/2高程处.
|
| 图 8 防渗墙中央纵剖面动应力包络图 (左侧为左岸,单位:kPa) Figure 8 Dynamic stress envelope diagram of the central longitudinal profile of cutoff wall (left side is left bank,unit:kPa) |
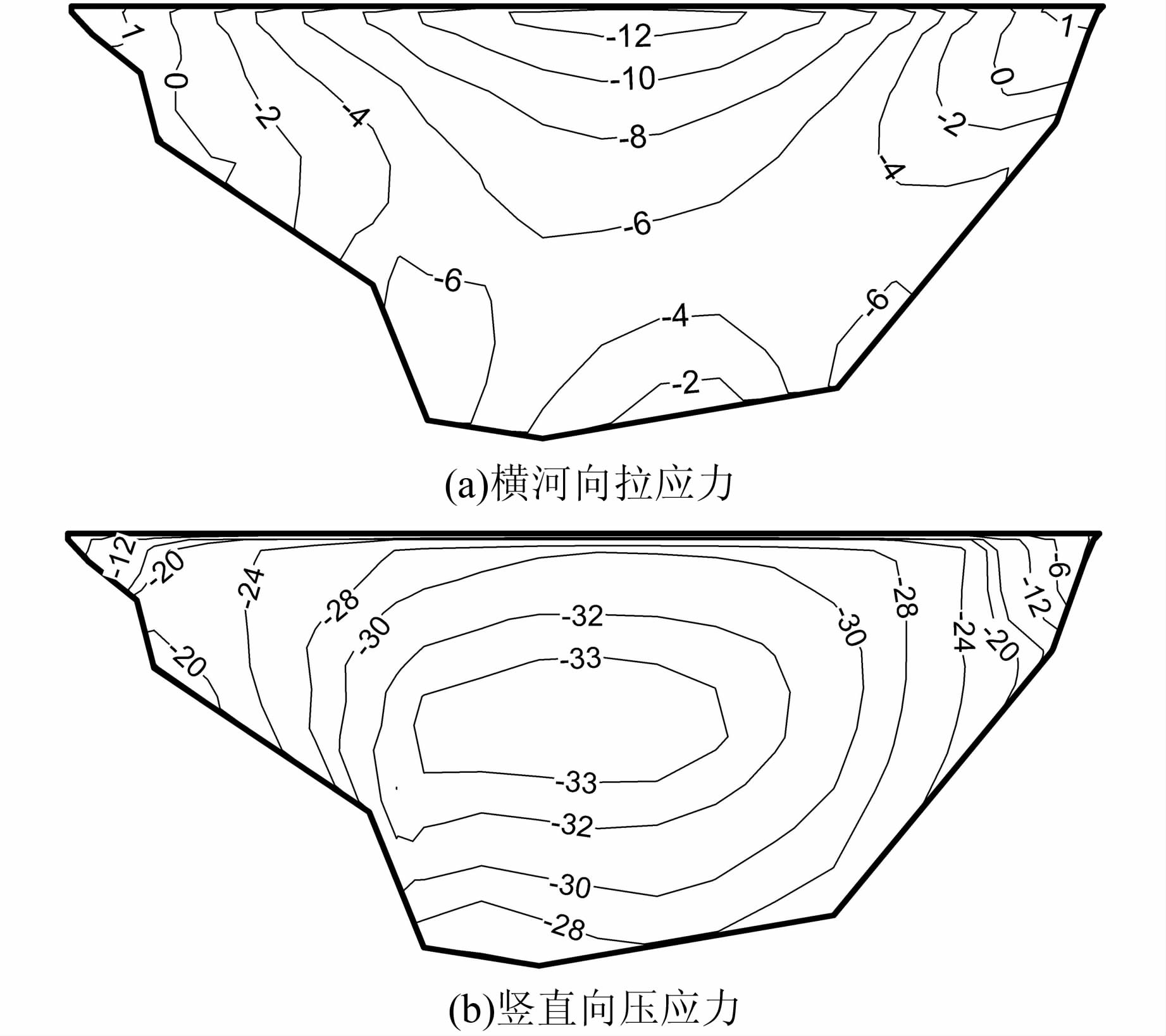
图 9为动静叠加后防渗墙中央纵剖面横河向和竖直向应力包络图.动静叠加后,防渗墙横河向应力分布规律与静力工况相比变化较小,仍基本处于全墙受压状态,但在左右岸墙顶局部区域存在拉应力,横河向最大拉应力为2.44 MPa,相比于静力工况下的2.20 MPa,增幅为10.9%,出现在防渗墙右岸侧顶部;动静叠加后,防渗墙竖直向应力分布规律变化也较小,仍基本处于全墙受压状态,仅在防渗墙两岸侧顶部出现小范围的拉应力区,墙身中部压应力值较大,并由河床中央向两岸侧逐渐减小,竖直向最大压应力由静力工况下的-33.32 MPa增加为-33.62 MPa,增幅为0.9%,出现在防渗墙中部约1/2高程处.
|
| 图 9 地震过程中防渗墙中央纵剖面应力包络图(左侧为左岸,单位:MPa) Figure 9 Stress envelope diagram of central longitudinal profile of cutoff wall during earthquake (left side is left bank,unit:MPa) |
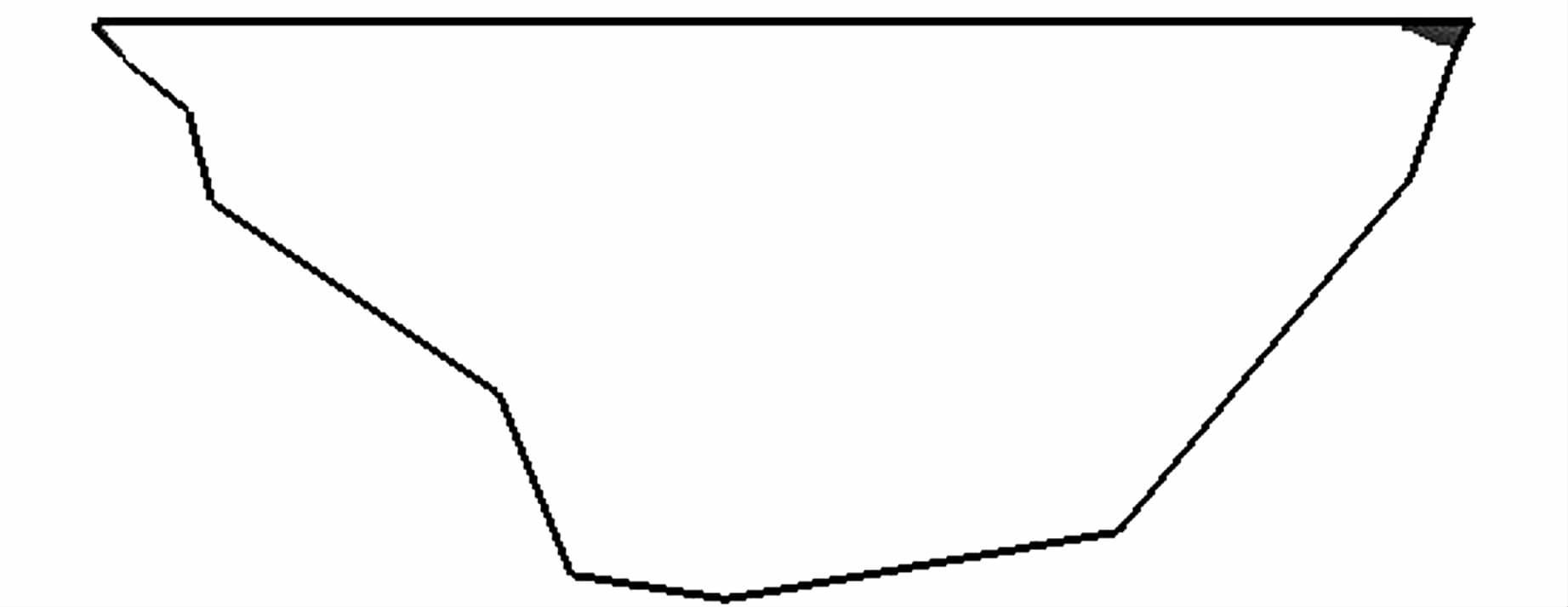
防渗墙混凝土强度等级为C40,C40混凝土的动态抗拉强度在静态抗拉强度上提高30%,为2.223 MPa[3].从以上分析可以看出,在地震作用下,防渗墙的横河向拉应力有一定程度的提高,但混凝土动态抗拉强度也相应地有所提高,因此防渗墙横河向拉应力超过抗拉强度的区域与静力状态相比基本不变.图 10为地震作用下防渗墙中央纵剖面横河向拉应力超过混凝土抗拉强度的区域.从图中可以看出,仅在防渗墙右岸顶部出现了小范围的超过混凝土抗拉强度的区域.竖直向压应力在地震波的作用下虽然有所增加,但增幅很小,仅为0.9%,说明8度地震对防渗墙的抗压安全性影响不大.
|
| 图 10 地震过程中防渗墙中央纵剖面 Figure 10 Area of transverse tensile stress exceeds concrete’s tensile strength during earthquake |
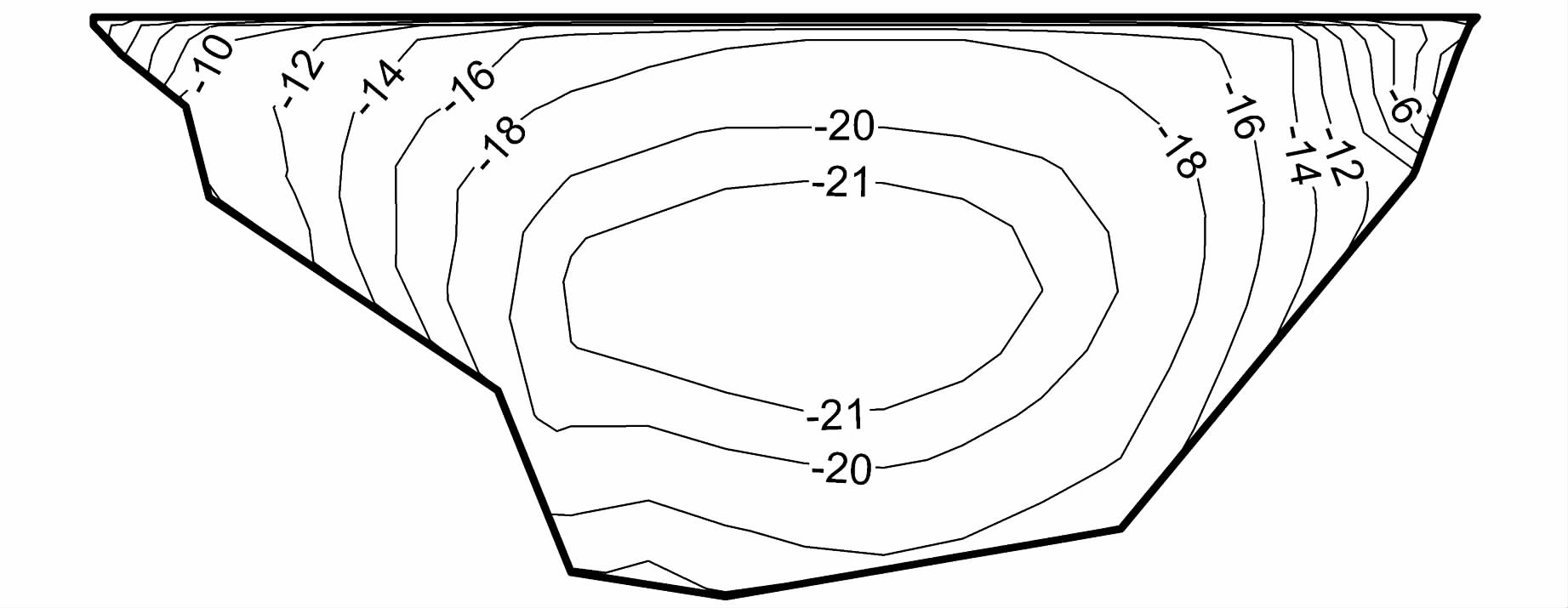
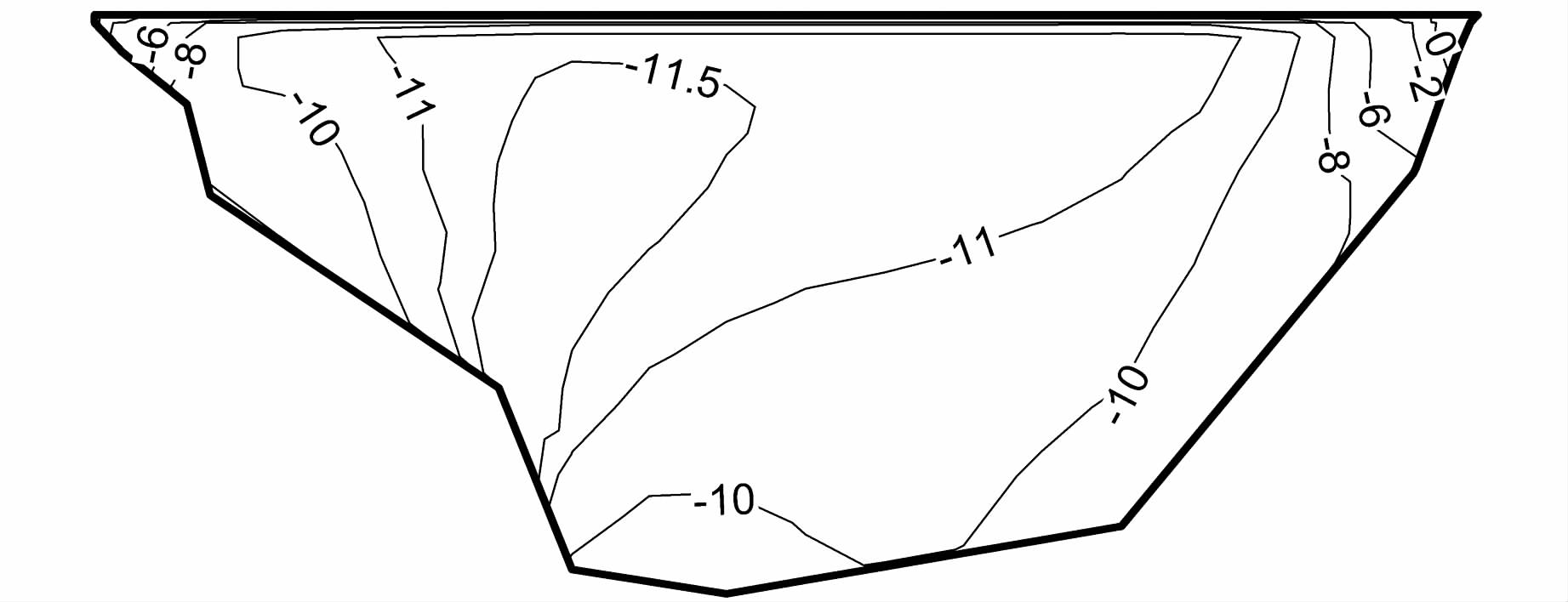
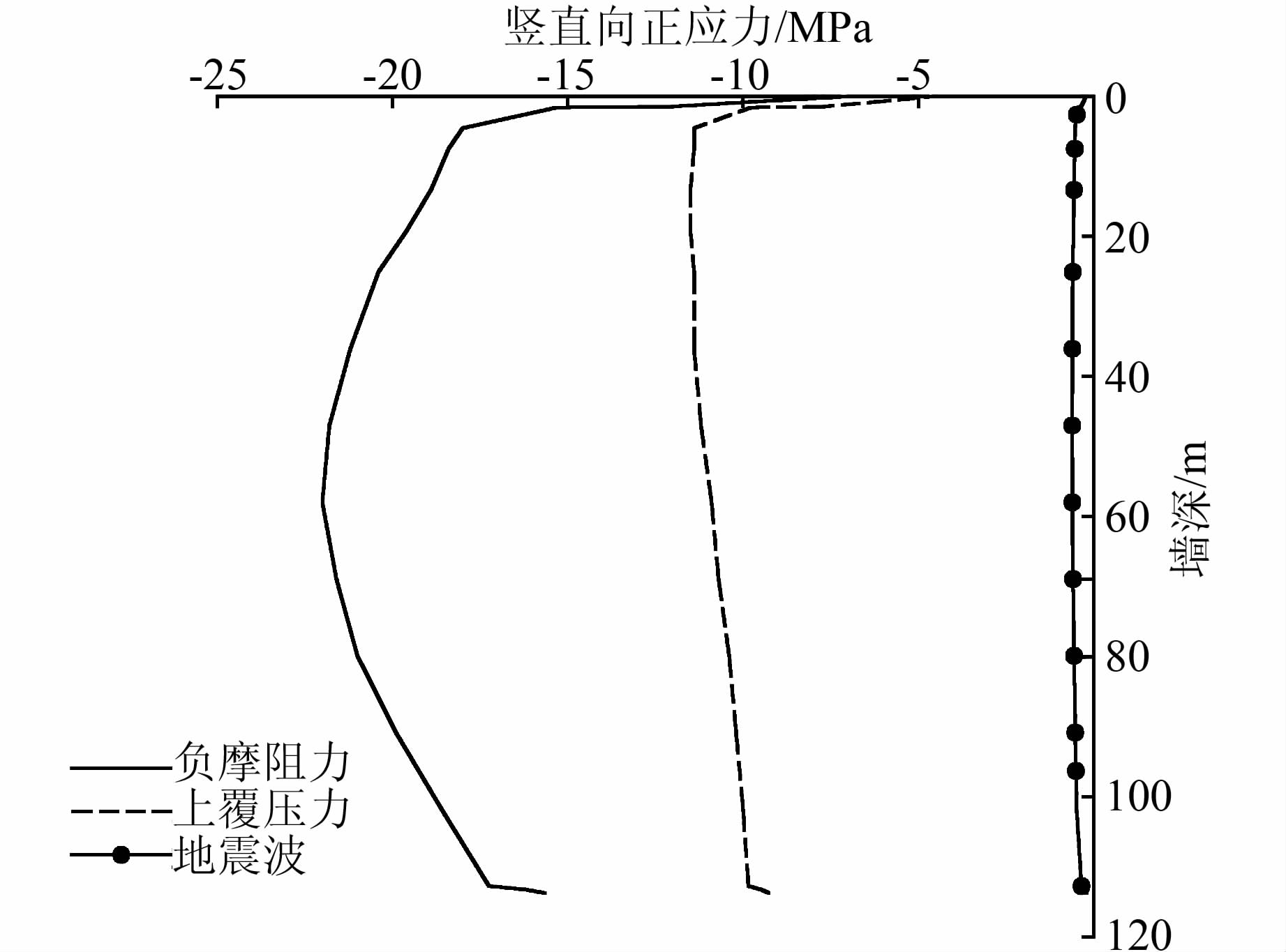
在地震工况,防渗墙竖直向应力除了受到上覆坝体压力及上、下游侧负摩擦阻力的影响之外,还要受到地震波的影响,分析它们各自对于防渗墙竖直向应力的影响,有利于更清楚地理解在地震作用下防渗墙竖直向应力的分布机制.图 11、图 12分别为墙体上、下游侧负摩擦阻力以及上覆坝体压力引起的防渗墙中央纵剖面的竖直向应力,地震波所引起的竖直向压应力见图 8(b),图 13为以上3种作用分别引起的防渗墙中央横断面竖直向应力分布.
|
| 图 11 负摩擦阻力引起的竖直向应力(左侧为左岸,单位:MPa) Figure 11 Contour map of vertical stress caused by frictional resistance(left side is left bank,unit:MPa) |
|
| 图 12 上覆坝体压力引起的竖直向应力(左侧为左岸,单位:MPa) Figure 12 Contour map of vertical stress caused by force acting on top of cutoff wall (left side is left bank,unit:MPa) |
|
| 图 13 3种作用分别引起的防渗墙中央横断面竖直向应力分布 Figure 13 Vertical stress distributions of central section caused by three kinds of effects |
从图 11、12中可以看出:由负摩擦阻力引起的竖直向应力分布规律与动静叠加后的分布规律(图 9(b))相似,最大压应力出现在防渗墙中部约1/2高程处,为-22.01 MPa;由上覆坝体压力引起的竖直向压应力最大值出现在左岸侧靠下部折坡附近,为-11.95 MPa,在中央横断面,由上覆坝体压力引起的竖直向压应力沿高度变化幅度较小;由地震波引起的竖直向压应力分布规律与负摩擦阻力类似,墙身中部压应力较大,并由河床中央向两岸侧逐渐减小,最大压应力为-630 kPa,出现在防渗墙中部约1/2高程处,在中央横断面,与上覆坝体压力引起的竖直向应力类似,竖直向动压应力沿高度变化幅度较小.
从图 13可以看出,在设计地震波的作用下,负摩擦阻力对防渗墙竖直向压应力的贡献最大,其次是上覆坝体压力,由地震波引起的压应力所占比例最小.统计应力分布结果可知,在竖直向总压应力最大值中,约65%来自于负摩擦阻力,约33.2%来自于上覆坝体压力,仅1.8%来自于地震波作用,说明设计地震波对防渗墙竖直向应力影响不大.
5 结论本文在防渗墙静力分析的基础上,采用时程法对其进行了动力反应分析,主要结论如下:
1) 在地震作用下,防渗墙的加速度和动位移反应较小,三个方向中顺河向的动力反应最为明显,动静叠加后,顺河向位移相对静力工况增加了4.6%.
2) 在地震过程中,防渗墙的应力分布规律与静力工况下基本一致.横河向应力仍表现为在左右岸墙顶存在局部拉应力区域,最大拉应力相比于静力工况增幅为10.9%,出现在墙体右岸侧顶部;在地震作用下,防渗墙横河向拉应力超过混凝土抗拉强度的区域相对静力状态而言变化很小.在竖直向,防渗墙仍基本处于全墙受压状态,最大压应力出现在防渗墙中部约1/2高程处,为-33.62 MPa,相比于静力工况下增加了0.9%,说明设计地震对防渗墙抗压安全性影响不大.
3) 在设计地震波的作用下,防渗墙竖直向压应力的最大值,约65%来自于负摩擦阻力,约33.2%来自于上覆坝体压力,仅1.8%来自于地震波作用,说明设计地震波对防渗墙竖直向应力影响不大.
| [1] |
吕洪旭, 陈科文, 邓建辉, 等. 瀑布沟大坝防渗墙应力分布特性及机理探讨[J].
人民长江, 2011, 42(10): 39–43.
Lü Hongxu, Chen Kewen, Deng Jianhui, et al. Discussion on mechanism and stress distribution features of diaphragm walls of Pubugou hydropower station during construction period[J]. Yangtze River, 2011, 42(10): 39–43. |
| [2] |
万宇豪, 何蕴龙, 潘迎. 黄金坪坝基廊道的抗震安全性[J].
武汉大学学报(工学版), 2015, 48(6): 751–757.
Wan Yuhao, He Yunlong, Pan Ying. Seismic safety of foundation gallery of Huangjinping rockfill dam[J]. Engineering Journal of Wuhan University, 2015, 48(6): 751–757. |
| [3] |
吴秋军, 傅少君. 子模型方法研究瀑布沟土石坝防渗结构[J].
武汉大学学报(工学版), 2006, 39(3): 55–59.
Wu Qiujun, Fu Shaojun. Study on seepage prevention structure for Pubugou earth-rock dam by sub-model method[J]. Engineering Journal of Wuhan University, 2006, 39(3): 55–59. |
| [4] |
赵吉坤, 朱小春, 石端学, 等. 子模型法在小湾拱坝结构诱导缝及检查廊道中的应用[J].
河海大学学报(自然科学版), 2007, 35(3): 298–301.
Zhao Jikun, Zhu Xiaochun, Dan Duanxue, et al. Application of sub-model method to inducement slot and check-up porch of Xiaowan arch dam[J]. Journal of Hohai University(Natural Sciences), 2007, 35(3): 298–301. |
| [5] |
刘晓青, 李同春, 闫园园, 等. 地震作用下混凝土坝孔口应力分析的动力子模型法[J].
水力发电学报, 2009(5): 88–91.
Liu Xiaoqing, Li Tongchun, Yan Yuanyuan, et al. Dynamic sub-model method for stress analysis of orifice in concrete dam under action of earthquake[J]. Journal of Hydroelectric Engineering, 2009(5): 88–91. |
| [6] |
朱伯芳.
有限单元法原理与应用[M]. 第2版.北京: 中国水利水电出版社, 1998.
Zhu Bofang. Theory and Application of the Finite Element Method[M]. The Second Edition.Beijing: China WaterPower Press, 1998. |
| [7] | Kullhaway F H. Geomechanical model for rock foun-dation settlement[J]. Geotech. Div,Proc.Am. Soc. Civ. Engrs, 1978: 211–227. |
| [8] |
万彪, 何蕴龙, 熊堃. 有厚度节理单元的开发与应用[J].
水电能源科学, 2008, 26(4): 63–66.
Wan Biao, He Yunlong, Xiong Kun. Development of joint element with thickness and its application[J]. Water Resources and Power, 2008, 26(4): 63–66. |
| [9] | Bandis S C, Lumsden A C, Barton N R. Fundamen-tals of rock joint deformation[J]. International Journal of Rock Mechanics and Mining Sciences, 1983, 20(6): 249–268. DOI:10.1016/0148-9062(83)90595-8 |
| [10] | Clough G W, Duncan J M. Finite element analysis of retaining wall behavior[J]. Journal of Soil Mechanics and Foundation Engineering Division, ASCE, 1971, 97(12): 1657–1673. |
| [11] |
熊堃, 何蕴龙, 曹学兴. 观音岩水电站混合坝插入式接头的抗震性能[J].
天津大学学报, 2010(7): 583–592.
Xiong Kun, He Yunlong, Cao Xuexing. Earthquake-resistant characteristics of inserted junction in composite dam of Guanyinyan Hydropower Station[J]. Journal of Tianjin University, 2010(7): 583–592. |
| [12] | Duncan J M, Byrne P, Wong K S, et al. Strength, stress strain and bulk modulus parameters for finite element analysis of stresses and movements in soil masses[R].Univ. of California, Barkeley, 1978. |
| [13] | Duncan M J, Chang Y C. Nonlinear analysis of stress and strain in soils[J]. Journal of the Soil Mechanics and Foundations Divi, 1970, 96(5): 1629–1653. |
| [14] | Iwan W D. On a class of models for the yielding behavior of continuous and composite systems[J]. Journal of Applied Mechanics, 1967, 34(3): 612. DOI:10.1115/1.3607751 |
| [15] | Martin G R, Seed H B, Finn W D. Effects of system compliance on liquefaction tests[J]. Journal of the Geotechnical Engineering Division, 1978, 104(4): 463–479. |
| [16] |
顾淦臣.
土石坝地震工程学[M]. 北京: 中国水利水电出版社, 2009.
Gu Ganchen. Earthquake Engineering of Earth and Rockfill Dams[M]. Beijing: China WaterPower Press, 2009. |
 2016, Vol. 49
2016, Vol. 49




