文章信息
- 陈柯兵, 郭生练, 何绍坤, 尹家波, 杨光
- CHEN Kebing, GUO Shenglian, HE Shaokun, YIN Jiabo, YANG Guang
- 基于月径流预报的三峡水库优化蓄水方案
- Optimal impounding operation of Three Gorges Reservoir based on monthly runoff forecasting
- 武汉大学学报(工学版), 2018, 51(2): 112-117
- Engineering Journal of Wuhan University, 2018, 51(2): 112-117
- http://dx.doi.org/10.14188/j.1671-8844.2018-02-003
-
文章历史
- 收稿日期: 2017-06-15
长江三峡水利枢纽工程的主要功能是防洪、发电、航运、供水和生态等.与初设阶段相比,三峡水库运用的外部条件发生了很大的变化.若仍按初设方案,每年汛末10月1日开始蓄水,库水位从汛限水位145 m逐步上升至175 m水位,则水库的蓄满率较低,三峡工程综合利用效益较差.
开展三峡水库提前蓄水优化调度方案研究,选择合理的起蓄时间和蓄水方式,对充分发挥水库的综合利用效益具有重要的理论价值和现实意义.李义天等[1]在分析三峡水库洪水规律的基础上,提出了在9月份分旬控制蓄水的方案,针对不同频率的洪水组合进行了调洪演算,得到了9月各旬相应的防洪限制水位,并对其发电效益进行了比较.刘心愿等[2]考虑了三峡水库防洪、发电、航运、生态和抗旱等综合利用要求,建立了多目标蓄水优化调度模型,对汛末防洪库容和蓄水调度图进行了优化研究.李雨等[3]建立了三峡水库提前蓄水的防洪风险与效益分析模型,从防洪风险和蓄水效益两个方面对多组蓄水方案进行了优选.上述研究均采用长系列资料作为模型的输入,以多年平均发电量、蓄满率等指标最大化为目标函数,其内涵是得到多年蓄水过程平均效益最大的调度规则.而实际上水库的优化调度显然与当月来水情况有关,不同情形的来水,其优化调度结果势必差异较大.
为了解决单一优化调度规则对不同来水情况适应性不佳的问题,可采用不同方法将历史来水系列分成若干类型,如系统聚类[4]、归纳演绎[5]、集对分析[6]、频率分析[7]等,针对不同类型来水情况进行分类优化,得到多种优化调度规则.但这些研究实际指导意义不强,未给出可操作性的预报方案,难以用于调度实践.
本文以三峡水库提前蓄水调度方案为研究对象,提出聚类—预报—优化的预报调度模式,其核心思想为:从历史资料中找到与预报结果接近的情景集,从中挖掘出的调度规则指导水库汛末蓄水调度.建立三峡水库月径流预报模型和蓄水期多目标优化调度模型,分析比较基于月径流预报模式与传统长系列优化、法定规则调度方案的优劣.
1 月径流预报模型 1.1 奇异谱分析奇异谱分析(Singular Spectrum Analysis, SSA)是一种广义功率谱,可将所观测到的一维时间序列转化为轨迹矩阵,并对轨迹矩阵进行分解、重构处理,从而提取出能代表原时间序列不同成分的各种信号,如周期信号、趋势信号、噪声信号等[8].奇异谱分析方法详见文献[9].
1.2 确定性预报模型人工神经网络(Artificial Neural Network, ANN)广泛运用于科学、工程等诸多领域,其具有并行性、非线性映射能力、鲁棒性和容错性、自学习和自适应等特点[10].通常,一个神经网络模型具有3层结构,即输入层、隐含层和输出层,层与层之间通过权重连接.其中,输入层作为数据输入层,隐含层作为数据处理层,输出层给出数据处理后的结果.本研究利用Matlab神经网络工具箱,构建3层BP神经网络,其中输入层分别为1、2、3、4、5、6、9、12个节点,隐含层7个节点,输出层1个节点,利用动态自适应性学习率的梯度下降算法训练得到ANN确定性预报模型.
支持向量机(Support Vector Machines,SVM)是基于结构风险最小化原则,将最优分类问题转化为求解凸二次规划问题,得到全局最优解,较好地解决了局部极小值的问题,同时在一定程度上克服了"维数灾"和"过学习"等传统困难,因此在文本过滤、数据挖掘、非线性系统控制等领域广泛应用[11].本研究利用SVM工具箱,选用σ为参数的Gauss径向基函数,分别采用前1、2、3、4、5、6、9、12月的径流数据作为自变量,当前月份月径流为因变量,利用遗传算法进行参数率定,得到SVM确定性预报模型.
1.3 模拟预报结果分析为预测三峡9月来水情况,实现月径流分类优化,运用奇异谱分析(SSA)方法对三峡水库历史月径流资料进行降噪处理,建立ANN、SVM月径流预报模型.利用ANN和SVM模型预测三峡水库的月径流前,需进行预报因子的选取,即确定ANN和SVM模型的输入变量.本研究分别选取当前月份前1、2、3、4、5、6、9、12个月的径流数据作为预报因子,利用1882~1988年实测月径流建立ANN、SVM确定性预报模型(预报全部月份).采用1989~2016年数据进行预报检验,为评判模型的模拟预测能力,采用《水文情报预报规范》推荐的两个指标,即纳什效率系数(NSE)、水量平衡系数(WB)进行分析,模拟预测结果见表 1.
| 模型 | 率定期(1882.1-1988.12) | 检验期(1989.1-2016.12) | |||
| NSE | WB | NSE | WB | ||
| ANN-1 | 0.665 | 1.006 | 0.633 | 1.025 | |
| ANN-2 | 0.920 | 1.010 | 0.885 | 1.041 | |
| ANN-3 | 0.939 | 1.001 | 0.904 | 1.016 | |
| ANN-4 | 0.947 | 1.000 | 0.930 | 1.014 | |
| ANN-5 | 0.946 | 1.000 | 0.929 | 1.011 | |
| ANN-6 | 0.948 | 1.000 | 0.926 | 1.021 | |
| ANN-9 | 0.948 | 0.999 | 0.929 | 1.003 | |
| ANN-12 | 0.949 | 1.005 | 0.927 | 0.999 | |
| SVM-1 | 0.651 | 0.970 | 0.618 | 0.984 | |
| SVM-2 | 0.925 | 0.993 | 0.915 | 1.008 | |
| SVM-3 | 0.936 | 0.996 | 0.928 | 1.006 | |
| SVM-4 | 0.946 | 0.997 | 0.942 | 1.015 | |
| SVM-5 | 0.949 | 0.998 | 0.941 | 1.018 | |
| SVM-6 | 0.949 | 0.999 | 0.941 | 1.022 | |
| SVM-9 | 0.945 | 0.998 | 0.937 | 1.015 | |
| SVM-12 | 0.946 | 0.999 | 0.936 | 1.016 | |
由表 1得出,SVM模型稍优于ANN模型,当采用前2个月及以上的径流数据作为预报因子,月径流ANN、SVM预报模型率定期和检验期纳什效率系数均接近或超过0.9,水量平衡系数均接近于1,预报结果良好.利用前4个月的径流数据作为预报因子,纳什效率系数即可达到最高,更多预报因子对指标提升不明显,即4个月以上数据对预报模型影响较弱,该结果可反映出三峡月径流与前4个月存在较强的关系.
2 蓄水模型和优化算法本研究利用蓄水调度线[2-3]作为调度规则,指导三峡水库蓄水调度.蓄水调度线能明确起蓄时间和蓄水进程,通过设置汛末控制水位满足防洪的要求,对充分发挥水库枯水期的综合利用效益具有重要的理论价值和现实意义.蓄水调度线如图 1所示,蓄水模型优化对象为蓄水调度线各时间点水位.从调度线光滑性、耗时及优化效果上考虑,设置蓄水调度线的时间步长为5 d,与现有三峡蓄水调度研究[2-3, 12]中5~10 d的时间步长保持一致.
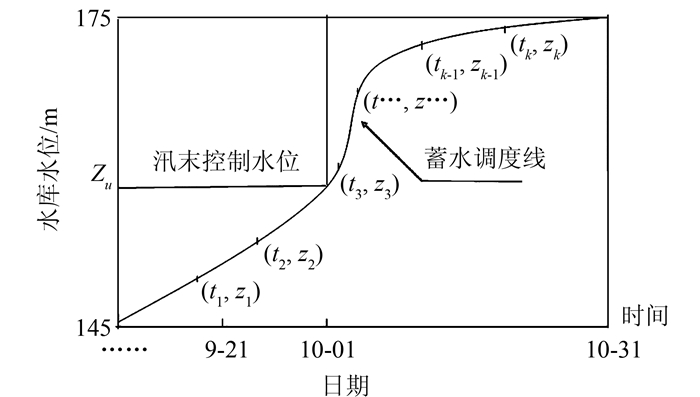
|
| 图 1 三峡水库蓄水调度线 Figure 1 Three Gorges Reservoir impounding operation curve |
以年均发电量最大和年均蓄水位最高为目标进行调度,目标函数如下所示:
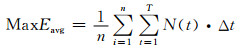 (1)
(1)
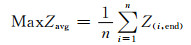 (2)
(2)
式中:n为模拟的年数;E为计划期T内发电量, kW·h;N(t)为第t时段的平均出力, kW;Z(i, end)为第i年蓄水期最后一天(10月31日)水库的水位.
年均蓄满率计算表达式如下:
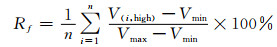 (3)
(3)
式中:V(i, high)为Z(i, end)对应的库容;Vmax为正常蓄水位对应的库容;Vmin为死库容.
2.2 约束条件1) 水量平衡约束:
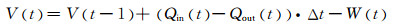 (4)
(4)
式中:V(t)为水库第t时段的库容, m3;Qin(t)和Qout(t)分别为水库第t时段的入库和出库平均流量, m3/s;Δt为计算时间步长;W(t)为水库第t时段的水分损失量, m3,如蒸散发、渗漏等.
2) 水库水位约束:
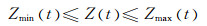 (5)
(5)
式中:Zmax(t)和Zmin(t)分别为水库第t时段的允许最大和最小水位, m.
3) 水库下泄流量约束:
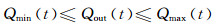 (6)
(6)
式中:Qmax(t)和Qmin(t)分别为水库第t时段的允许最大和最小下泄流量, m3/s,一般由下游生态、航运要求和水库下游的防洪任务确定.
4) 电站出力约束:
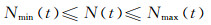 (7)
(7)
式中:Nmax(t)和Nmin(t)分别为水库第t时段的允许最大和最小出力, kW.
5) 边界约束:
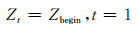 (8)
(8)
式中:Zbegin为水库起蓄时水位, m, 其值取汛限水位值.
2.3 NSGA-Ⅱ优化算法NSGA-Ⅱ算法由Deb[13]于2000年提出,以其快速的运行效果和良好的收敛性目前被广泛应用于多目标优化计算.近年来该算法已被我国学者广泛应用于水库多目标调度的研究中,并取得了良好的效果[14-16],算法的具体计算流程参阅文献[17].
本研究利用NSGA-Ⅱ优化算法将前述蓄水调度线中各时间点水位编码为染色体,利用蓄水调度线作为调度规则进行模拟调度,计算年均发电量及蓄水位,其中种群个数为30,进化代数为200,交叉和变异概率分别取0.9和0.1.
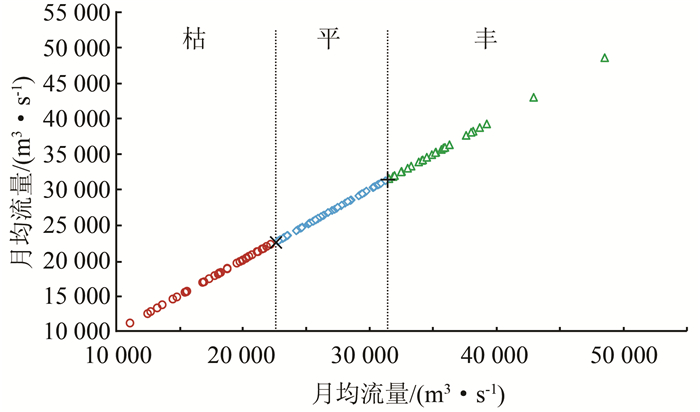
3 结果分析 3.1 聚类分析为实现对9月不同来水情况下三峡水库蓄水方案的优化选择,采用K-means聚类算法将三峡1882-2016年9月的历史径流进行分类处理.该算法是聚类分析中使用最为广泛的算法之一,它把n个对象根据他们的属性分为k个聚类,使所获得的聚类满足同一聚类中对象的相似度较高,而不同聚类中对象的相似度较小.聚类的种类k需事先给出,本研究中k值定为3,将三峡月均径流分为丰、平、枯3类,见图 2,月均流量超过31 365 m3/s为丰水月(25 a),小于22 562 m3/s为枯水月(40 a),两者之间为平水月(70 a).
|
| 图 2 9月份月均流量聚类结果 Figure 2 Monthly mean runoff clustering results in September |
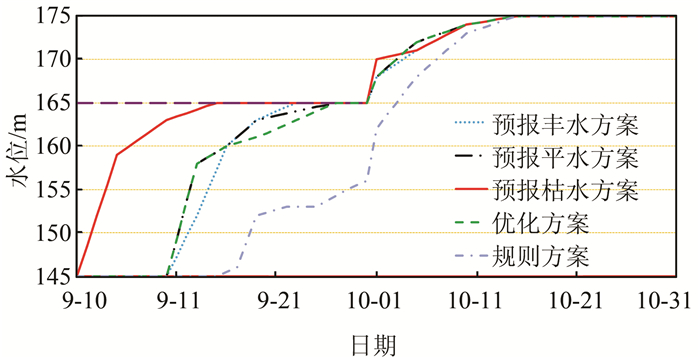
按照《三峡优化调度方案》[18](以下简称规则方案),水库可以自9月15日开始蓄水,9月25日蓄至153 m(不超过153 m),9月30日不超过156 m,10月底蓄满.按照近年来水库实际的蓄水实施计划[19-20] (以下简称优化方案),水库可以自9月10日开始蓄水,9月份控制水位不超过165 m,10月底蓄满.本研究中分别以上述两种方案作为优化边界调节,将三峡1882-2016年历史长系列径流资料作为模型的输入,采用NSGA-Ⅱ优化算法得到优化后的蓄水调度线,如图 3所示.
|
| 图 3 不同优化蓄水调度线对比 Figure 3 Comparison of different optimized refill operation curves |
为分析规则方案与优化方案对9月不同来水情况下三峡水库蓄水的应用效果,分别将9月来水丰、平、枯的年份,利用上述优化调度线模拟调度,结果如表 2所示.从表中可以看出,优化方案平均效益高于规则方案.当9月为丰、平水时,采用规则方案与优化方案均能取得较好的效益.但当9月为枯水时,采用规则方案与优化方案,蓄水效果均不佳,9月底平均水位分别为154.94 m、162.31 m,均未达到方案所规定的9月底限制水位,从而影响了水库10月的蓄水.上述分析说明,当三峡水库9月来水为枯,即月平均流量小于22 562 m3/s时,需考虑在现有规则方案与优化方案上进一步提前蓄水.
| 调度方案 | 1882-2016年 | 模拟调度平均效益 | |||
| 蓄水期发电/(亿kW·h) | 9月底水位/m | 10月底蓄水位/m | |||
| 规则方案 | 9月15日起蓄 | 25年丰 | 297.61 | 157.43 | 175.00 |
| 70年平 | 251.98 | 156.18 | 174.75 | ||
| 40年枯 | 193.30 | 154.94 | 171.78 | ||
| 平均 | 243.04 | 156.04 | 173.92 | ||
| 优化方案 | 9月10日起蓄 | 25年丰 | 316.07 | 165.00 | 175.00 |
| 70年平 | 266.12 | 165.00 | 175.00 | ||
| 40年枯 | 198.89 | 162.31 | 173.10 | ||
| 平均 | 255.45 | 164.20 | 174.44 | ||
| 预报方案 | 9月10日起蓄 | 25年丰 | 316.77 | 165.00 | 175.00 |
| (增量/增幅) | (0.70/0.22%) | (0) | (0) | ||
| 70年平 | 266.30 | 165.00 | 175.00 | ||
| (增量/增幅) | (0.18/0.07%) | (0) | (0) | ||
| 9月1日起蓄 | 40年枯 | 205.72 | 164.17 | 173.80 | |
| (增量/增幅) | (6.83/3.43%) | (1.86/1.15%) | (0.70/0.40%) | ||
| 平均 | 257.70 | 164.75 | 174.64 | ||
| (增量/增幅) | (2.25/0.88%) | (0.55/0.33%) | (0.20/0.11%) | ||
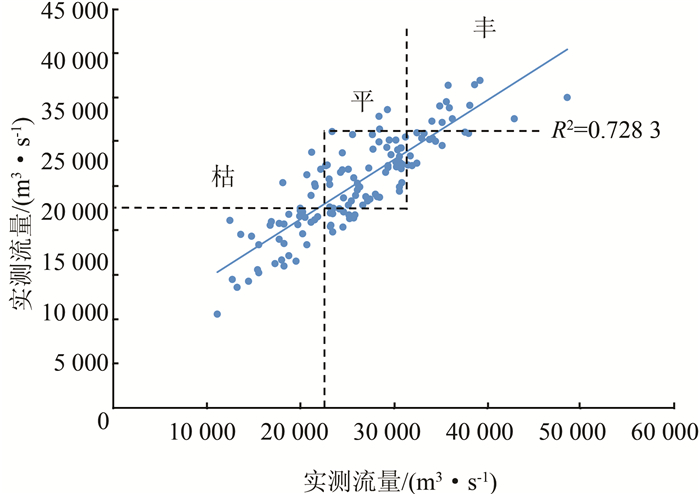
为检验上述预报模型对三峡水库月径流分类优化的适用性,直观表现出9月径流与前4个月存在的关系,将SVM-4模型1882-2016年9月预报值与实测值建立散点图,见图 4.从图中可以看出,预报值与实测值的关系比较密切,相关系数达到0.728 3. 3个矩形区域即预报模型可准确将9月来水进行丰、平、枯分类,可以看出SVM-4模型绝大部分预报值均位于区域内或分界线相邻处.故该预报模型可在一定程度上应用于三峡水库9月的径流预报,即认为8月末可较为准确预测9月份的来水情况,为三峡水库蓄水调度提供科学依据.在实际工作中,还可根据9月份的定量降雨预报信息,一并估计判断9月来水的丰、平、枯情况.显然,9月来水为枯不利于蓄水,来水为丰则可考虑加大出力,提前知晓可为调度决策人员提供更加灵活的操作空间.
|
| 图 4 SVM-4模型9月预报值与实测值 Figure 4 Observed and SVM-4 forecasted runoff in September |
若使用预报模型提前知晓9月来水为枯,由于9月10日起蓄,蓄水效果不佳.故考虑进一步提前起蓄时间为9月1日,将1882-2016年中共计40年9月为枯水的资料作为蓄水优化模型的输入,得到9月为枯水情况下,起蓄时间为9月1日的优化蓄水调度线(预报枯水方案),如图 3所示.该优化调度线利用9月初的来水,较快提升蓄水位,与优化方案相比,其9月10日水位大幅提升.同理可得到9月10日起蓄的预报丰、平水方案.
对于9月不同来水情况的年份,采用相应预报方案与优化方案模拟调度,结果如表 2所示.从表中可以看出,当9月为丰、平水时,预报方案稍稍好于前述较优的优化方案,提升幅度不大.平均而言,采用预报方案可比优化方案提高发电效益0.88%,9月底水位提高0.33%,10月底蓄水位提高0.11%.当9月为枯水时,预报方案提升效益尤为显著,采用预报枯水方案比优化方案可大幅提高发电效益3.43%,9月底水位提高1.15%.10月底蓄水位提升幅度不大,为0.70 m(0.40%),但由于水库的水面面积随着水位增高而增大,计算年均蓄满率,可增加3.44%.上述结果说明,若9月来水为丰、平,9月10日起蓄方案效益良好,考虑预报提升不大.若8月末通过预报模型提前知晓9月来水为枯,将起蓄时间提前至9月1日,采用预报枯水方案调度可大幅提高三峡水库蓄水期发电量及蓄满率.但蓄水时间的提前,不可避免地带来一定的防洪风险,在实际蓄水调度中需得到重视.
4 结论针对三峡水库现有优化蓄水研究所得到的长系列平均效益最大的调度规则未结合预报信息、难以应用于实际调度的问题,提出聚类—预报—优化的预报调度模式,建立了预报模型与三峡水库优化蓄水模型,采用NSGA-Ⅱ算法优化蓄水调度线.主要结论如下:
1) 利用前4个月的径流数据作为预报因子,可获得最优的预报模型.SVM-4模型预测三峡水库月径流效果良好,可较为准确地判断9月的月均来水情况,其结果可为三峡水库蓄水调度提供依据.
2) 若9月来水为丰、平,9月10日起蓄方案效益良好,考虑预报提升不大.若9月来水为枯,推荐将起蓄时间进一步提前至9月1日,该方案可提高三峡水库发电效益3.43%,蓄满率3.44%.
该预报调度模式可为中长期预报结果运用于水库调度提供参考,此外结合短期、实时预报进一步修正蓄水调度线,确保防洪风险可控,值得深入研究.
| [1] |
李义天, 甘富万, 邓金运. 三峡水库9月分旬控制蓄水初步研究[J].
水力发电学报, 2006, 25(1): 61–66.
Li Yitian, Gan Fuwan, Deng Jinyun. Three Gorges Reservoir in September to control the water storage of a preliminary study[J]. Journal of Hydroelectric Engineering, 2006, 25(1): 61–66. |
| [2] |
刘心愿, 郭生练, 刘攀, 等. 考虑综合利用要求的三峡水库提前蓄水方案研究[J].
水科学进展, 2009, 20(6): 851–856.
Liu Xinyuan, Guo Shenglian, Liu Pan, et al. Study on advanced water storage scheme of Three Gorges Reservoir considering comprehensive utilization[J]. Advances in Water Science, 2009, 20(6): 851–856. |
| [3] |
李雨, 郭生练, 刘攀, 等. 三峡水库提前蓄水的防洪风险与效益分析[J].
长江科学院院报, 2013, 30(1): 8–14.
Li Yu, Guo Shenglian, Liu Pan, et al. Analysis of flood risk and benefit of the Three Gorges Reservoir in advance refill operation[J]. Journal of Yangtze River Scientific Research Institute, 2013, 30(1): 8–14. |
| [4] |
周晓阳, 张勇传. 洪水的分类预测及优化调度[J].
水科学进展, 1997, 8(2): 123–129.
Zhou Xiaoyang, Zhang Yongchuan. Classification and optimization of flooding[J]. Advances in Water Science, 1997, 8(2): 123–129. |
| [5] |
马寅午, 顾宁昌. 防洪系统洪水分类预测优化调度方法[J].
水利学报, 1997(4): 1–8.
Ma Yinwu, Gu Ningchang. Purpose scheduling method for flood forecasting of flood control system[J]. Journal of Hydraulic Engineering, 1997(4): 1–8. |
| [6] |
陈柯兵, 郭生练, 杨光, 等. 基于年径流分类的水库优化调度函数研究[J].
水资源研究, 2016, 5(6): 573–582.
Chen Kebing, Guo Shenglian, Yang Guang, et al. Reservoir optimal operation function based on annual runoff classification[J]. Journal of Water Resources Research, 2016, 5(6): 573–582. |
| [7] |
刘强, 钟平安, 徐斌, 等. 三峡及金沙江下游梯级水库群蓄水期联合调度策略[J].
南水北调与水利科技, 2016, 14(5): 62–70.
Liu Qiang, Zhong Pingan, Xu Bin, et al. Cooperation strategy of cascade reservoirs in the lower reaches of the Three Gorges and Jinsha River[J]. South-to-North Water Transfers and Water Science & Technology, 2016, 14(5): 62–70. |
| [8] |
汪芸, 郭生练, 李响. 奇异谱分析在中长期径流预测中的应用研究[J].
人民长江, 2011, 42(9): 4–7.
Wang Yun, Guo Shenglian, Li Xiang. Singular spectrum analysis in the application of medium and long-term runoff forecast[J]. Yangtze River, 2011, 42(9): 4–7. |
| [9] |
何绍坤, 郭生练, 刘章君, 等. 水库月径流概率预报研究[J].
水资源研究, 2017, 6(1): 1–8.
He Shaokun, Guo Shenglian, Liu Zhangjun, et al. Probability forecast of monthly reservoir inflow[J]. Journal of Water Resources Research, 2017, 6(1): 1–8. |
| [10] | Chau K W, Cheng C T. Real-time prediction of water stage with artificial neural network approach[C]// AI 2002: Advances in Artificial Intelligence. Springer Berlin Heidelberg, 2002: 715. |
| [11] |
周惠成, 王福兴, 梁国华. 碧流河水库后汛期汛限水位及控制运用方式[J].
水科学进展, 2009, 20(6): 857–862.
Zhou Huicheng, Wang Fuxing, Liang Guohua. Decision-making on reservoir flood control level and its control manner in post-flooding seasons for Biliuhe Reservoir[J]. Advances in Water Science, 2009, 20(6): 857–862. |
| [12] |
闵要武, 张俊, 邹红梅. 基于来水保证率的三峡水库蓄水调度图研究[J].
水文, 2011, 31(3): 27–30.
Min Yaowu, Zhang Jun, Zou Hongmei. Research on impounding schemes for the Three Gorges Reservoir based on inflow guaranteed frequency[J]. Hydrology, 2011, 31(3): 27–30. |
| [13] | Deb K, Agrawal S, Pratap A, et al. A fast elitist nondominated sorting genetic algorithm for multi-objective optimization: NSGA-Ⅱ[J]. Lecture Notes in Computer Science, 2000, 1917: 849–858. DOI:10.1007/3-540-45356-3 |
| [14] |
杨光, 郭生练, 李立平, 等. 考虑未来径流变化的丹江口水库多目标调度规则研究[J].
水力发电学报, 2015, 34(12): 54–63.
Yang Guang, Guo Shenglian, Li Liping, et al. Study on multi-objective scheduling rules of Danjiangkou reservoir considering future runoff variation[J]. Journal of Hydroelectric Engineering, 2015, 34(12): 54–63. DOI:10.11660/slfdxb.20151206 |
| [15] |
贠汝安, 董增川, 王好芳. 基于NSGA2的水库多目标优化[J].
山东大学学报:工学版, 2010, 40(6): 124–128.
Yun Ru'an, Dong Zengchuan, Wang Haofang. NASGA2-based reservoir multi-objective optimization[J]. Journal of Shandong University: Engineering Science, 2010, 40(6): 124–128. |
| [16] |
肖刚, 解建仓, 罗军刚. 基于改进NSGA-Ⅱ的水库多目标防洪调度算法研究[J].
水力发电学报, 2012, 31(5): 77–83.
Xiao Gang, Xie Jiancang, Luo Jungang. Study on reservoir multi-objective flood control scheduling algorithm based on improved NSGA-Ⅱ[J]. Journal of Hydroelectric Engineering, 2012, 31(5): 77–83. |
| [17] | Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182–197. DOI:10.1109/4235.996017 |
| [18] |
中华人民共和国水利部. 三峡水库优化调度方案[S], 2009.
The People's Republic of China Ministry of Water Resources. Three Gorges Reservoir Optimal Scheduling Program[S], 2009. |
| [19] |
国家防汛抗旱总指挥部. 关于三峡工程2015年试验性蓄水实施计划的批复[R], 2015.
National Flood Control and Drought Relief Headquarters. Reply on the Implementation of the Pilot Refill Project of the Three Gorges Reservoir in 2015[R], 2015. |
| [20] |
国家防汛抗旱总指挥部. 关于三峡工程2016年试验性蓄水实施计划的批复[R], 2016.
National Flood Control and Drought Relief Headquarters. Reply on the Implementation of the Pilot Refill Project of the Three Gorges Reservoir in 2016[R], 2016. |
 2018, Vol. 51
2018, Vol. 51




