文章信息
- 赵国, 郭江
- ZHAO Guo, GUO Jiang
- 微电网中电动汽车无线充电优化的调度策略
- Research on optimal scheduling strategy of electric vehicles wireless charging in microgrid
- 武汉大学学报(工学版), 2018, 51(8): 745-752
- Engineering Journal of Wuhan University, 2018, 51(8): 745-752
- http://dx.doi.org/10.14188/j.1671-8844.2018-08-013
-
文章历史
- 收稿日期: 2018-01-12
2. 武汉大学动力与机械学院,湖北 武汉 430072
2. School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China
以风电、光伏发电为代表的可再生能源的开发利用日益得到关注和重视,然而其发电出力的随机性、波动性则是电力系统运行面临的巨大挑战,传统的以发电跟踪负荷波动实现系统平衡、以发电控制调整系统运行状态的运行策略和控制手段将难以为继.利用可控负荷的调度来追踪可再生能源的出力变化,促进可再生能源的就地消纳,从而调整系统运行状态,将在未来的电力系统运行中发挥重要的作用[1-4].
另外,以低碳排放和减少环境污染为目标的电动汽车技术也得到了快速的发展,目前已成为各国政府、汽车制造商和能源企业关注的焦点[5-7].电动汽车充电负荷具有一定的可控性,恰当的充电控制不仅能够抑制、消除电动汽车对电网的不利影响,而且能够支撑电网运行.研究表明,电动汽车低排放的优势只有在以低碳电力为主的区域才比较显著,而在以燃煤发电为主的区域则不太明显.这意味着只有尽可能多地采用风电、光伏等可再生能源为电动汽车充电,才能充分发挥电动汽车的减排效益.因此,电动汽车充电与风电、光伏发电协调互补成为国内外学者研究的热点[8-15].
与有线接触式充电相比,以无线充电方式给电动汽车提供能源供给具有使用方便、安全、无火花及触电危险,无积尘和接触损耗,无机械磨损和相应的维护问题,可适应多重恶劣环境和天气[16-22].因此,电动汽车无线充电方式更具灵活性,便于对其进行调度,从而更有利于促进光伏发电的就地消纳,提高光伏发电的利用率.
在此背景下,本文以无线充电方式的电动汽车充电作为可控负荷,提出一种将充电站内电动汽车起始充电时间作为控制对象的有序充电优化调度策略.一方面,以光伏发电利用率最大化为目标,实现对光伏发电的就地消纳;另一方面,考虑充电站内电动汽车充电成本,引入分时电价,建立了光伏发电与电动汽车无线充电的双目标优化模型.采用差分元胞遗传算法[23]对所建模型进行求解,由此得到的非支配解集收敛性较好,Pareto前沿分布均匀,算法有效可行.通过对Pareto解集中的各非支配解进行规范化排序后可以选择电动汽车充电最佳方案.
仿真结果表明,本文提出的优化调度策略可以实现电动汽车充电成本最小化与光伏发电利用率最大化的有效统一.
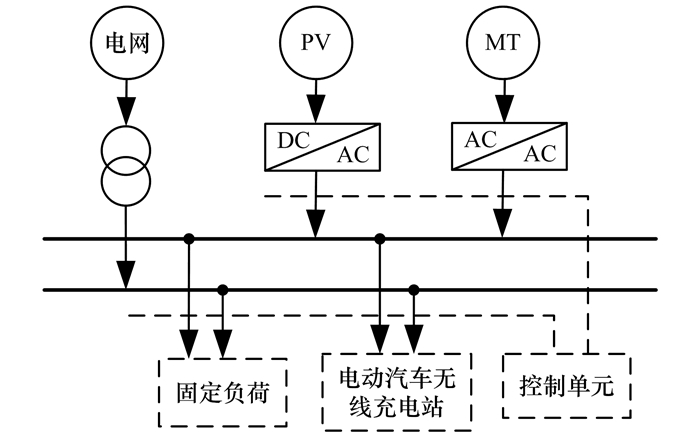
1 电动汽车无线充电优化调度模型 1.1 含电动汽车无线充电站微网本文构建如图 1所示的含电动汽车无线充电站的微网结构.分布式电源选择微型燃气轮机(Micro Turbine,MT)和光伏发电(PV).
|
| 图 1 含电动汽车无线充电站和光伏发电的微电网 Figure 1 Structure of microgrid system including EVs wireless charging station and PV generation |
当微电网系统稳定运行时,系统满足功率平衡:
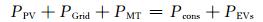 (1)
(1)
式中:PPV为光伏发电输出功率;PGrid为系统从电网吸收的功率;PMT为燃气轮机发电功率;Pcons为系统固定负荷;PEVs为微电网中电动汽车充电总功率.在优化周期内,MT一直处于额定功率输出状态,固定负荷减去MT供电部分称为基本净负荷,基本净负荷及可控负荷由光伏发电和配电网共同供电,并且优先使用光伏发电.由此可得
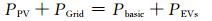 (2)
(2)
由式(2)可以知道,当光伏发电最大输出功率小于基本负荷及可控负荷之和时,则光伏发电功率将全部被利用,而当光伏发电输出功率大于基本负荷及可控负荷之和时,则光伏发电系统降低功率运行,即会出现弃光现象.
因此,本文将电动汽车充电负荷作为可控负荷,通过微电网中电动汽车无线充电进行优化调度,对光伏发电的输出功率进行跟踪,从而提高光伏发电的利用率.
1.2 电动汽车动力电池充电功率模型目前,电动汽车车用电池主要有铅酸电池、镍氢电池和锂电池,其中锂电池最具商业化运行的趋势.对电池寿命较好的一种充电方法是恒流-恒压的2段式充电法,即在充电的前期采用恒流充电方式,当电池电压上升至电池的最大允许充电电压后改为恒压充电方式,以此来避免充电初期的充电电流过大和恒流充电后期过充电的现象.充电功率可表示为
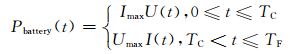 (3)
(3)
式中,Imax和Umax分别表示电池充电的最大电流和最大电压,TC和TF分别表示电池恒流充电时间和总充电时间,这些参数是由电池种类及充电特性所确定的常数.
当采用恒流-恒压充电方式时,整个充电过程中,90%以上的时间是进行恒流充电,因此,可忽略恒压充电过程以简化模型.为了便于建模分析,在恒流限压阶段,其充电电压用最大充电电压线性表示,则式(3)可表示为
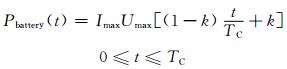 (4)
(4)
式中:k同样是由电池种类及充电特性所确定的常数.
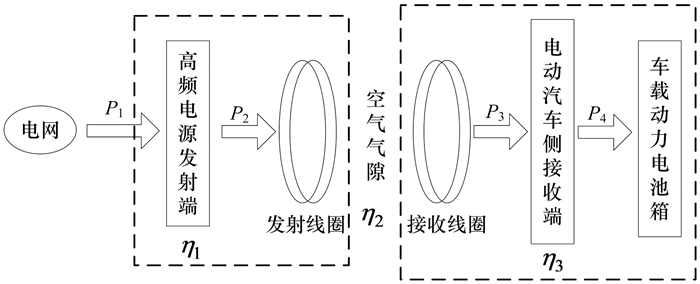
1.3 电动汽车无线充电功率模型电动汽车无线充电技术,是通过埋设于地表的1次线圈(发射线圈)与固定于车辆底盘的2次线圈(接收线圈)之间的电磁耦合来传输电能对车载动力电池进行充电.通过电磁共振的无线传输方式可以实现传输距离0.5 m以上千瓦级的电能传输,可以满足电动汽车无线充电要求.电动汽车无线充电系统结构如图 2所示.
|
| 图 2 电动汽车无线充电系统结构图 Figure 2 Structure of EV wireless charging system |
图 2中,P1为系统从电网吸收的功率,P2为电源发射功率,P3为接收功率,P4为电池充电功率,它们之间满足如下关系:
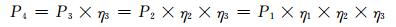 (5)
(5)
式中:η1和η3为开关电源效率;η2为无线电能传输效率.由式(4)、(5)可得电动汽车无线充电负荷率为
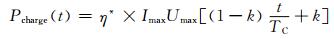 (6)
(6)
式中:η*为无线充电综合效率.
为了优化分析,将充电总时长均分为M个阶段,则每个阶段时长为TM=TC/M,利用等面积法则,每个阶段的充电可以用平均功率P表示.对于阶段m有
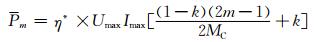 (7)
(7)
式(7)即为电动汽车无线充电分阶段功率模型,其精度与M的取值相关,M越大,模型的精度越高,计算量也越大,反之亦然.
将优化周期T均分为N个时段,且每个时段时长和TM相同,即TN=T/N=TC/M.则第n个时段的电动汽车充电总功率为
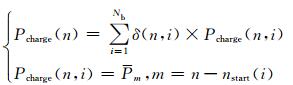 (8)
(8)
式中:Nb为电动汽车总数; nstart(i)为第i辆电动汽车开始充电的时段数; δ(n, i)为第i辆电动汽车的充电状态,1表示充电,0表示不充电.
因为电池是电动汽车的核心且成本相当昂贵,考虑短时间内多次充电启停会大大降低电池的寿命,因此引入电池充电连续性约束条件,所有电池连续充电直至充满,即δ(n, i)在开始充电后的连续M个时段均为1,如下式所示:
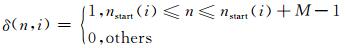 (9)
(9)
定义光伏发电利用率(PV Power Utilization Ratio,PPUR)为电动汽车充电优化调度周期中被利用的光伏发电功率占光伏发电可输出最大功率的比例:
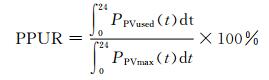 (10)
(10)
式中,PPVused(t)和PPVmax(t)分别为t时刻被利用的光伏发电功率及光伏电站可输出的最大功率.
以光伏发电利用率最大化为优化目标,离散化的目标函数可表示为
 (11)
(11)
式中,第n个时段被利用的光伏发电功率可由下式计算得到:
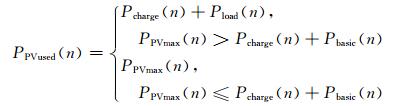 (12)
(12)
根据我国工业用电分时电价,考虑电动汽车充电成本,将充电站充电总费用最小作为优化目标.电动汽车充电费用可表示为
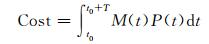 (13)
(13)
式中:t0为充电起始时间;t0+T为充电结束时间;T为充电周期;M(t)和P(t)分别为充电时刻t对应的实时电价和充电功率.对式(13)进行离散化后可得目标函数:
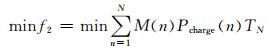 (14)
(14)
式中,M(n)为第n个时段的实时电价.
从式(11)、(12)、(14)可以看出,2个优化目标都取决于各个时段的电动汽车充电总功率Pchagre(n).若已知每台电动汽车的起始充电时段nstart(i),则可以得到每台电动汽车在优化周期内各个时段的充电状态δ(n, i)和充电功率Pcharge(n, i),从而可以计算出各个时段电动汽车充电的总功率Pchagre(n).
因此,可以将电动汽车起始充电时段作为优化对象,综合式(7)~(14),可以得到电动汽车无线充电双目标优化调度模型:
 (15)
(15)
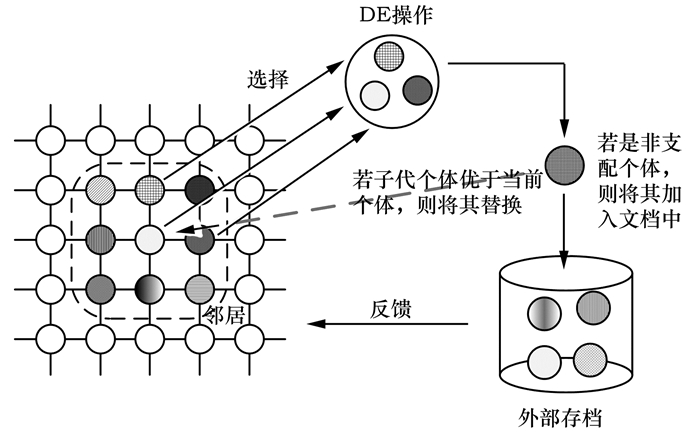
多目标元胞遗传(MOCell)算法是在经典元胞遗传算法的基础上引入反馈机制,并且采用基于距离的拥挤机制,得到的一种基于元胞自动机理论的多目标遗传算法.DECell算法则是在MOCell的基础上改进的一种算法,其基本思想是用MOCell作为搜索引擎,采用差分演化(Differential Evolution,DE)中的繁殖机制来替代遗传算法中的交叉、变异等传统的操作算子产生新个体,通过反馈机制从外部文档中选取若干个体来替换当前种群中随机选取的相同数量的个体,使种群不断进行更新操作,从而使获得的Pareto前沿的解集能在保持良好的均匀性和分布广度的同时,朝着最优前端不断逼近,其算法原理图如图 3所示.
|
| 图 3 DECell基本原理图 Figure 3 Basic principle chart of DECell algorithm |
采用DECell算法对前文建立的电动汽车无线充电优化调度模型进行计算,基本步骤如下.
1) 初始化算法参数:设置种群规模P,外部文档大小D,缩放因子F,交叉因子CR,反馈个体数C以及进化代数G.
2) 随机生成初始种群:采用实数制编码,随机生成初始种群[X1,X2,…,XP],并且生成一个外部空文档:
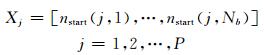 (16)
(16)
3) 获取邻居:将种群个体放置在二维的环形网络中,定义邻居结构类型.
4) DE操作产生子代个体:对当前种群中的每个个体,从当前个体Xr1, G邻居中选取2个个体Xr2, G和Xr3, G,r1、r2和r3分别为它们的索引位置,按下式进行交叉操作得到Vi, G= (vi, 1, G, vi, 2, G, …, vi, j, G, …, vi, N, G):
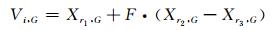 (17)
(17)
对其父本个体Xi, G= (xi, 1, G, xi, 2, G, …, xi, j, G, …, xi, N, G), 按下式进行变异操作得到新的子代个体Ui, G+1 = [ui, 1, G+1, ui, 2, G+1, …, ui, j, G+1, …, ui, N, G+1]:
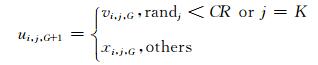 (18)
(18)
式中:K为[0, N-1]之间的整数.
5) 适应度评估:根据式(11)和式(14)计算个体适应度值,如果子代个体支配当前个体,则用子代个体替换当前个体,并将该个体存放到外部文档中.
6) 反馈:对外部文档中的非支配个体进行拥挤距离计算与排序,删除拥挤距离小的多余个体,然后通过反馈机制选取若干个体替换当前种群中相同数量的个体.
7) 终止条件判断:采用最大迭代次数作为算法终止条件,如果达到规定的迭代次数则停止运行,输出非支配解集,否则转向步骤(4).
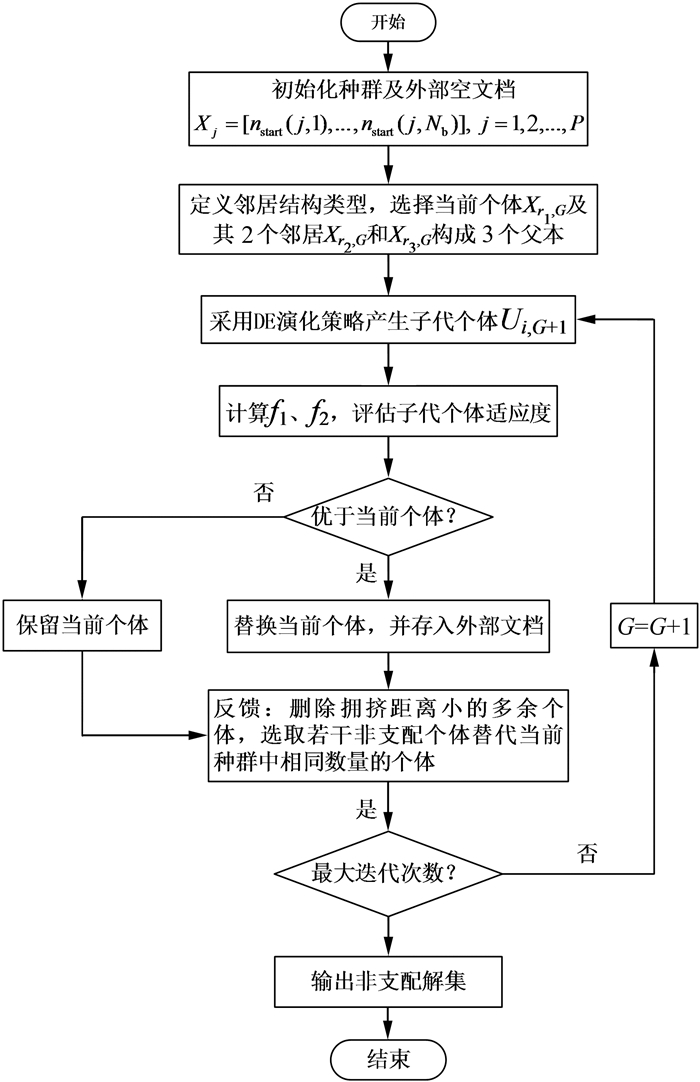
基于DECell算法的双目标优化调度模型求解流程如图 4所示.
|
| 图 4 DECell算法流程图 Figure 4 Flowchart of DECell algorithm |
本文以某单位停车场及其所在的区域作为前文所构建的微网系统,对该单位停车场内100辆电动汽车进行无线充电优化调度.优化周期为上班时间8:00~19:00,将优化周期分为12个时段,即每个时段TN为1 h.
3.1 基础数据及仿真参数 3.1.1 电动汽车无线充电参数为了便于计算,假设所有电动汽车电池规格统一,充电特性一致,电池箱的标称容量为60 kW·h,且起始电量SOC0均为20%,充电时长TC为4 h,无线充电综合效率η*为65%.可以计算获得电动汽车无线充电4个时段的平均充电功率Pm,如表 1所示.
| 时段/h | 1 | 2 | 3 | 4 |
| 功率/kW | 29.76 | 28.5 | 11.61 | 3.96 |
根据私家车上下班时间的出行规律,用正态分布函数N(9,0.52)和N(18,0.52)来描述各电动汽车到达工作区充电及离开的时间分布情况.
3.1.2 微电网负荷参数假定微网中的MT以额定功率200 kW提供电能.该微电网的固定负荷可以在日前预测,优化周期各时段负荷如表 2所示.
| 时段/h | 固定负荷/kW |
| 8 | 503.6 |
| 9 | 624.2 |
| 10 | 864.5 |
| 11 | 851.3 |
| 12 | 576.1 |
| 13 | 384.5 |
| 14 | 359.6 |
| 15 | 372.2 |
| 16 | 395.4 |
| 17 | 623.8 |
| 18 | 864.5 |
| 19 | 851.7 |
以某地区分布式光伏发电站实际发电数据为参考,假设光伏最大输出功率可以在日前预测获得,预测结果如表 3所示.
| 时段/h | 最大出力/kW |
| 8 | 479 |
| 9 | 763.68 |
| 10 | 627.32 |
| 11 | 850.04 |
| 12 | 998.68 |
| 13 | 1 533.32 |
| 14 | 1 446.72 |
| 15 | 1 008.32 |
| 16 | 1 459 |
| 17 | 1 530.32 |
| 18 | 1 040.68 |
| 19 | 456.48 |
参考江苏省分时电价,负荷谷时段为0:00~8:00, 共8 h,对应的电价为0.365元/kW·h时;负荷峰时段为9:00~12:00及18:00~21:00,共8 h,对应的电价为0.869元/kW·h;其余时间段为负荷平时段,对应的电价为0.687元/kW·h.
3.1.5 算法参数设置DECell算法基本参数如表 4所示.
| 参数 | 种群规模P | 缩放因子F | 交叉因子CR | 外部种群D | 迭代次数G | 反馈个体数C |
| 大小 | 200 | 0.8 | 0.2 | 10 | 1 000 | 20 |
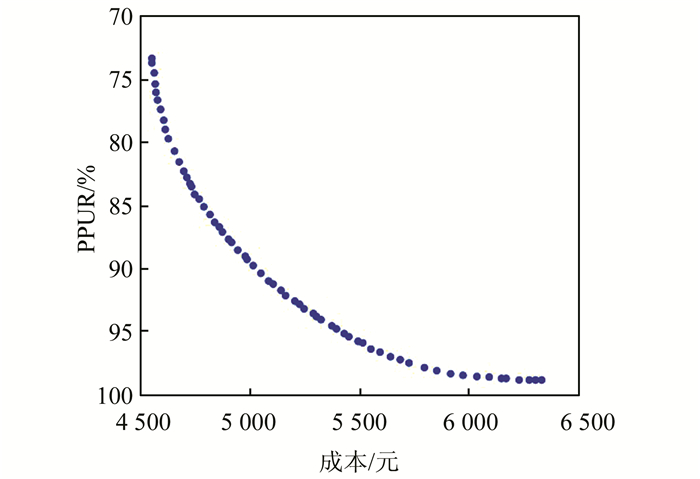
采用DECell算法对建立的双目标优化调度模型进行求解,得到的相应的Pareto前沿如图 5所示.
|
| 图 5 DECell算法获得的Pareto前沿 Figure 5 Pareto front gained by DECell algorithms |
从图 5可以看出,DECell算法由于结合了DE策略和MOCell两者的优点,得到的Pareto前沿分布较为均匀,收敛性也很好,可以验证该算法在求解本文所提出的双目标优化问题的有效性.
对得到的Pareto解集中的各非支配解进行规范化排序,各个非支配解的规范值为
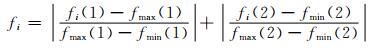 (19)
(19)
式中:fi为Pareto解集中第i个解的规范值;fi(1)和fi(2)分别为第i个解对目标1和目标2的适应度值;fmax(1)和fmin(1)分别为所有解中对目标1适应度的最大值和最小值;fmax(2)和fmin(2)分别为所有解中对目标2适应度的最大值和最小值.
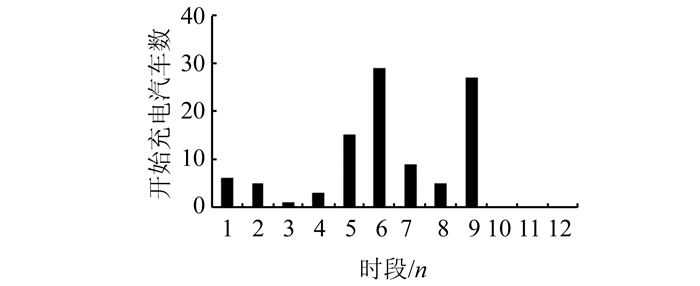
选择Pareto解集中规范值最小的解作为最优解,该最优解对应的即为优化调度控制策略.根据优化得到的每台电动汽车的起始充电时段,可以计算得到优化周期内各时段开始充电的电动汽车数量,如图 6所示.
|
| 图 6 各时段开始充电电动汽车数 Figure 6 Distribution of EVs starting charging |
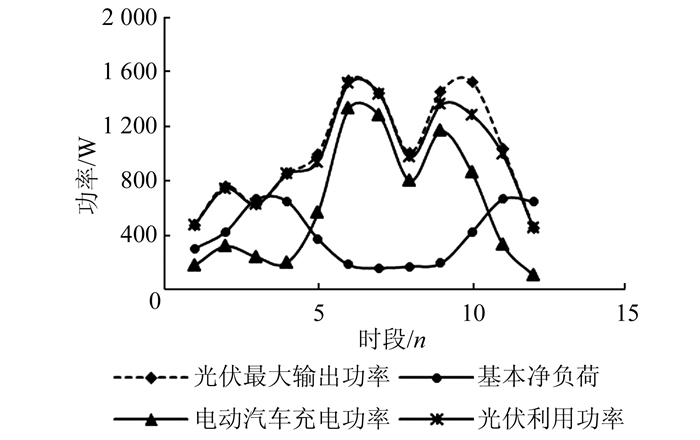
由各个时段内电动汽车的充电状况,可以计算出各时段电动汽车充电的总功率,从而可得到优化调度下微电网系统的功率平衡分析情况,如图 7所示.
|
| 图 7 微电网功率平衡图 Figure 7 Power balance of microgrid |
从图 7中可以看出,优化调度下的充电控制策略可以将电动汽车充电时段进行时移,使得电动汽车充电负荷与基本净负荷的和值在优化周期内的各个时段尽可能都大于对应时段的光伏发电最大输出功率,从而可以使光伏发电功率尽可能多地被负荷消耗,避免光伏发电功率弃用现象的发生.与随到随充的充电方式相比,优化调度控制下的充电策略可以明显提高微电网中光伏发电的利用率,如表 5所示.
| % | ||
| 充电策略 | PPUR | 提高 |
| 未优化充电方式 | 73.4 | |
| 优化充电方式 | 93.2 | 19.8 |
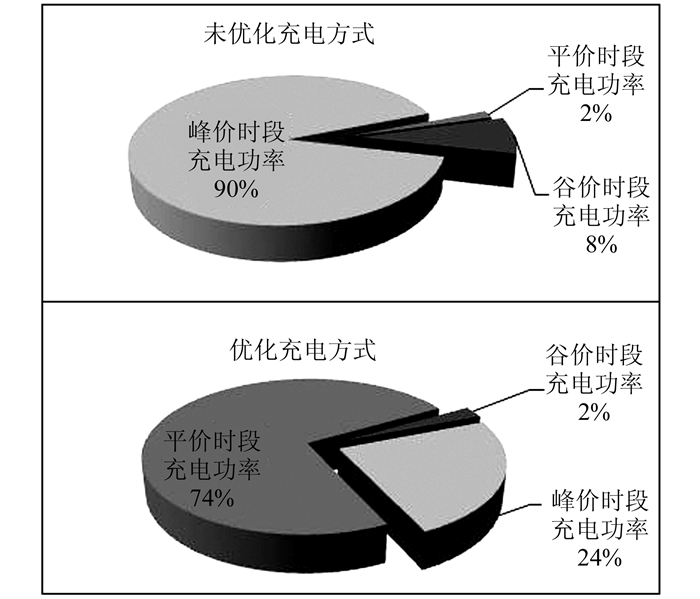
由于所建立的优化模型,在考虑最大化光伏发电利用率的同时,也将用户充电成本最小化作为优化目标.因此,得到的优化调度策略可以兼顾光伏发电利用率和电动汽车充电总成本.2种充电方式下电动汽车充电功率在不同电价时段的分布情况及充电成本分别如图 8和表 6所示.
|
| 图 8 2种方式的充电功率时段分布 Figure 8 Power distribution under different charging patterns |
| 充电策略 | 成本/元 | 降低/% |
| 未优化充电方式 | 6 094.2 | |
| 优化充电方式 | 5 335.8 | 12.44 |
从图 8可以看出,优化调度充电方式可以将大量的电动汽车充电功率需求从电价峰值时段转移到平价时段,从而降低充电成本.
从表 6可以看出,优化调度充电方式下电动汽车的总充电成本与未优化的充电方式相比有明显的降低.
综合以上分析结果可以看出,所提出的优化调度策略通过电动汽车充电负荷来跟踪光伏发电输出功率的变化,对提高光伏发电利用率具有较好的效果.但是,本文在优化时,为了便于计算,将电动汽车电池参数及微电网相关参数作了简化,同时电动汽车充电方式都是设定为无线充电方式,在以后的研究中还需要进一步考虑参数变化以及电动汽车无线充电的渗透率对优化调度结果的影响.
4 结论本文首先构建了含光伏发电及电动汽车无线充电站的微电网系统,建立了电动汽车无线充电功率模型,然后以光伏发电利用率最大化及充电成本最小化为目标建立了电动汽车无线充电双目标优化调度模型.采用DECell算法对模型进行求解,得到的非支配解集具有较好的收敛性,Pareto前沿分布均匀,算法有效可行.通过对非支配解集的规范化排序可以得到最优解,从而得到了一种以电动汽车起始充电时间为控制对象的电动汽车无线充电优化控制策略.通过仿真结果分析,可得到如下结论:
1) 采用的电动汽车无线充电优化控制策略,一方面可以提高光伏发电功率的利用率,促进光伏发电的就地消纳;另一方面通过引入分时电价,可以降低电动汽车的总充电成本,同时也间接起到了对区域电网负荷削峰填谷的作用,提高了系统的综合经济效益和环境效益.
2) 为进一步研究光伏发电和其他可再生能源的就地消纳以及电动汽车充电的能源供给方式,提供了一定的基础.
| [1] |
江岳春, 王志刚, 杨春月, 等. 微网中可控负荷的多目标优化策略[J].
电网技术, 2013, 37(10): 2875–2880.
Jiang Yuechun, Wang Zhigang, Yang Chunyue, et al. Multi-objective optimization strategy of controllable load in microgrid[J]. Power System Technology, 2013, 37(10): 2875–2880. |
| [2] |
陈征, 刘念, 路欣怡, 等. 考虑换电储备的电动汽车光伏换电站动态功率分配方法[J].
电工技术学报, 2014, 29(4): 306–315.
Chen Zheng, Liu Nian, Lu Xinyi, et al. Dynamic power distribution method of PV-based battery switch stations considering battery reservation[J]. Transactions of China Electrotechnical Society, 2014, 29(4): 306–315. DOI:10.3969/j.issn.1000-6753.2014.04.039 |
| [3] | Wang Zhaojian, Chen Ying, Mei Shengwei, et al. Optimal expansion planning of isolated microgrid with renewable energy resources and controllable loads[J]. IET Renewable Power Generation, 2017, 11(7): 931–940. DOI:10.1049/iet-rpg.2016.0661 |
| [4] | Solanki B V, Raghurajan A, Bhattacharya K. Including smart loads for optimal demand response in integrated energy management systems for isolated microgrids[J]. IEEE Transactions on Smart Grid, 2017, 8(4): 1739–1748. DOI:10.1109/TSG.2015.2506152 |
| [5] |
胡泽春, 宋永华, 徐智威, 等. 电动汽车接入电网的影响与利用[J].
中国电机工程学报, 2012, 32(4): 1–10.
Hu Zechun, Song Yonghua, Xu Zhiwei, et al. Impacts and utilization of electric vehicles integration into po-wer systems[J]. Proceedings of the CSEE, 2012, 32(4): 1–10. |
| [6] |
孙晓明, 王玮, 苏粟, 等. 基于分时电价的电动汽车有序充电控制策略设计[J].
电力系统自动化, 2013, 37(1): 191–195.
Sun Xiaoming, Wang Wei, Su Su, et al. Coordinated charging strategy for electric vehicles based on time-of-use price[J]. Automation of Electric Power System, 2013, 37(1): 191–195. |
| [7] |
王锡凡, 邵成成, 王秀丽, 等. 电动汽车充电负荷与调度控制策略综述[J].
中国电机工程学报, 2013, 33(1): 1–10.
Wang Xifan, Shao Chengcheng, Wang Xiuli, et al. Survey of electric vehicle charging load and dispatch control strategies[J]. Proceedings of the CSEE, 2013, 33(1): 1–10. |
| [8] |
肖湘宁, 陈征, 刘念, 等. 可再生能源与电动汽车充放电设施在微网中的集成模式与关键问题[J].
电工技术学报, 2013, 28(2): 1–14.
Xiao Xiangning, Chen Zheng, Liu Nian, et al. Integrated mode and key issues of renewable energy sources and electric vehicles' charging and discharging facilities in microgrid[J]. Transactions of China Electrotechnical Society, 2013, 28(2): 1–14. DOI:10.3969/j.issn.1000-6753.2013.02.001 |
| [9] |
陈征, 肖湘宁, 路欣怡, 等. 含光伏发电系统的电动汽车充电站多目标容量优化配置方法[J].
电工技术学报, 2013, 28(6): 238–248.
Chen Zheng, Xiao Xiangning, Lu Xinyi, et al. Multi-objective optimization for capacity configuration of PV-based electric vehicle charging stations[J]. Transactions of China Electrotechnical Society, 2013, 28(6): 238–248. DOI:10.3969/j.issn.1000-6753.2013.06.035 |
| [10] |
张学清, 梁军, 张利, 等. 计及风光电源的一种地区电网电动汽车充电调度方法[J].
电工技术学报, 2013, 28(2): 28–35.
Zhang Xueqing, Liang Jun, Zhang Li, et al. Approach for plug-in electric vehicles charging scheduling consi-dering wind and photovoltaic power in Chinese Regional Power Grids[J]. Transactions of China Electrotechnical Society, 2013, 28(2): 28–35. DOI:10.3969/j.issn.1000-6753.2013.02.004 |
| [11] | Haque A N M M, Ibn Saif A U N, Nguyen P H, et al. Exploration of dispatch model integrating wind generators and electric vehicles[J]. Applied Energy, 2016, 183: 1441–1451. DOI:10.1016/j.apenergy.2016.09.078 |
| [12] | Zeng Bo, Feng Jiahuan, Zhang Jianhua, et al. An optimal integrated planning method for supporting gro-wing penetration of electric vehicles in distribution systems[J]. Energy, 2017, 126: 273–284. DOI:10.1016/j.energy.2017.03.014 |
| [13] | Yao L, Damiran Z, Lim W H. Optimal charging and discharging scheduling for electric vehicles in a parking station with photovoltaic system and energy storage system[J]. Energies, 2017, 10(4): 1–20. |
| [14] | Vahedipour-Dahraie M, Rashidizaheh-Kermani H, Najafi H R. Coordination of EVs participation for load frequency control in isolated microgrids[J]. Applied Sciences, 2017, 7(6): 1–16. |
| [15] | Hafez O, Bhattacharya K. Optimal design of electric vehicle charging stations considering various energy resources[J]. Renewable Energy, 2017, 107: 576–589. DOI:10.1016/j.renene.2017.01.066 |
| [16] |
曹玲玲, 陈乾宏, 任小勇, 等. 电动汽车高效率无线充电技术的研究进展[J].
电工技术学报, 2012, 27(8): 1–13.
Cao Lingling, Chen Qianhong, Ren Xiaoyong, et al. Review of the efficient wireless power transmission technique for electric vehicles[J]. Transactions of China Electrotechnical Society, 2012, 27(8): 1–13. |
| [17] |
黄学良, 吉青晶, 谭林林, 等. 磁耦合谐振式无线电能传输系统串并式模型研究[J].
电工技术学报, 2013, 28(3): 171–176.
Huang Xueliang, Ji Qingjing, Tan Linlin, et al. Study on series-parallel model of wireless power transfer via magnetic resonance coupling[J]. Transactions of China Electrotechnical Society, 2013, 28(3): 171–176. DOI:10.3969/j.issn.1000-6753.2013.03.024 |
| [18] |
谭林林, 黄学良, 黄辉, 等. 基于频率控制的磁耦合共振式无线电力传输系统传输效率优化控制[J].
中国科学:技术科学, 2011, 41(7): 913–919.
Tan Linlin, Huang Xueliang, Huang Hui, et al. Transfer efficiency optimal control of magnetic resonance coupled system of wireless power transfer based on frequency control[J]. Science China Technology Science, 2011, 41(7): 913–919. |
| [19] | Knaisch K, Huck T, Gratzfeld P. Analysis and optimization of a solenoid coupler for wireless electric vehicle charging[J]. Wireless Power Transfer, 2017, 4(1): 13–20. DOI:10.1017/wpt.2016.11 |
| [20] | Zeng Hulong, Yang Shuitao, Fang Z P. Design consideration and comparison of wireless power transfer via harmonic current for PHEV and EV wireless charging[J]. IEEE Transactions on Power Electronics, 2017, 32(8): 5943–5952. DOI:10.1109/TPEL.2016.2616111 |
| [21] | Mahmud M H, Elmahmoud W, Barzegaran1 M R, et al. Efficient wireless power charging of electric vehicle by modifying the magnetic characteristics of the transmitting medium[J]. IEEE Transactions on Magnetics, 2017, 53(6): 1–5. |
| [22] | Dai Zhongyu, Wang Junhua, Long Mengjiao, et al. A witricity-based high-power device for wireless charging of electric vehicles[J]. Energies, 2017, 10(3): 1–14. |
| [23] |
刘自发, 庞铖铖, 王泽黎, 等. 基于云理论和元胞自动机理论的城市配电网空间负荷预测[J].
中国电机工程学报, 2013, 33(10): 98–105.
Liu Zifa, Pang Chengcheng, Wang Zeli, et al. Spatial load forecasting for distribution network based on cloud theory and cellular automata[J]. Proceedings of the CSEE, 2013, 33(10): 98–105. |
 2018, Vol. 51
2018, Vol. 51



