文章信息
- 曾希, 董飞飞, 廖恒, 杜国锋
- ZENG Xi, DONG Feifei, LIAO Heng, DU Guofeng
- 跨断层埋管力学行为的多参数模拟分析
- Multiparameter simulation analysis of mechanical behavior of buried pipeline crossing fault
- 武汉大学学报(工学版), 2017, 50(6): 874-880
- Engineering Journal of Wuhan University, 2017, 50(6): 874-880
- http://dx.doi.org/10.14188/j.1671-8844.2017-06-012
-
文章历史
- 收稿日期: 2017-06-12
近年来,埋地管道在断层运动下的反应研究一直备受关注,Newmark等[1]1975年首次提出埋地管道在断层作用下的简化模型,该模型假设断层位移完全由轴向变形吸收,忽略了土横向作用力和管道的抗弯刚度,计算结果偏不安全,后来Kennedy等[2]考虑了横向管土的相互作用,改进了这一方法,接着Wang等[3]做了进一步改进,将变形后的管道简化为单一曲率弯曲大变形梁和弹性地基梁.以上模型均为梁模型,不能很好地分析管道局部屈曲的大变形情况.随着计算机技术的快速发展,有限元软件在埋地管道研究领域得到了很好的应用,Takada等[4]用梁壳混合模型分析了在正、逆断层错动下埋地钢制管道的变形,并首次考虑了管道断面的变形.慕园等[5]利用有限元软件ABAQUS进行了逆断层作用下的管土作用分析.刘铭刚等[6]建立管土耦合模型,进行了基于应变的管道设计.刘啸奔等[7]从解析分析、数值模拟、试验研究3个方面论述了国内外的研究进展,冯启民等[8]分析了管道在大位移断层作用下的屈曲效应.王滨等[9]提出了地震断层作用下埋地管道的等效分析模型.范锋、丰晓红等[10, 11]建立了跨断层埋地输气管道的有限元模型,并提出了管道最大应变值的简化计算公式.尽管众多学者对埋地管道进行了深入的研究,但对场地土体类型等多参数下的埋地管道分析甚少.本文采用有限元软件ABAQUS,研究不同断层位移、管径、壁厚、断层及场地类型等参数下埋地管道的力学行为,并分析了它们对管道受力与变形的影响.
1 有限元模型的建立 1.1 管材及土层模型的建立为对断层错动下埋地管道的反应进行深入研究,本文取管道计算长度为50 m,选用X60管材.土体材料选用砂黏土和石灰岩,土层的计算区域长宽高为5 m×5 m×50 m,跨断层宽度取1 m,穿越角取60°,埋深为1.5 m,管道和土体的其他参数见表 1、2.
| 材料 | 外径/m | 壁厚/m | 弹性模量 /GPa |
密度 /(kg·m-3) |
弹性屈服 强度/MPa |
弹性屈服 应变/m |
塑性屈服 强度/MPa |
塑性屈服 应变/m |
| X60 | 1 | 0.015 | 210 | 7 850 | 458 | 0.002 2 | 517 | 0.040 |
| 材料 | 弹性模 量/GPa |
内聚力 /MPa |
膨胀角 /(°) |
泊松比 | 摩擦角 /(°) |
密度 /(kg·m-3) |
| 砂黏土 | 0.008 | 5.00 | 0 | 0.37 | 20.0 | 1 900 |
| 石灰岩 | 43.96 | 22.79 | 0 | 0.23 | 44.1 | 2 710 |
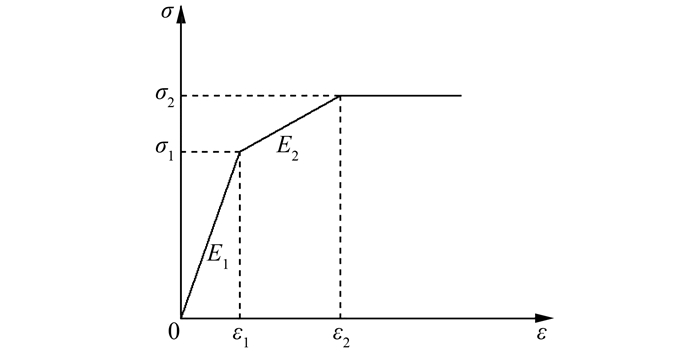
管道的本构关系曲线采用规范[12]中的三折线模型,在ABAQUS中定义X60钢材的弹性和塑性相关参数.如图 1所示,管道的应力应变状态分为弹性、弹塑性和塑性3个阶段,其中,ε1和σ1表示管道的弹性屈服应变和弹性屈服应力;ε2和σ2表示管道的塑性屈服应变和塑性屈服应力;E1和E2分别为管道在弹性区和塑性区的材料模量.土体的本构关系采用ABAQUS软件中自带的M-C模型,不考虑土体的剪胀角.由于M-C模型采用了非关联流动法则,因此,在用有限元进行求解时必须采用非对称求解器.
|
| 图 1 管道钢的三折线模型 Figure 1 Trilinear model sketch for pipeline steel |
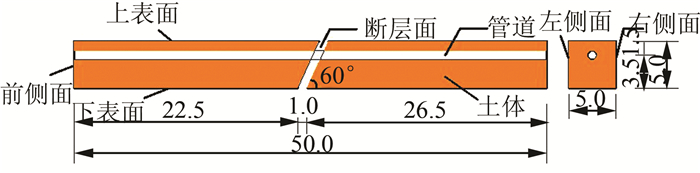
考虑到管道和土层材料的非线性,在断层的运动过程中会存在着位移不协调的情况,本文将管道模拟为4节点减缩积分薄壳单元,土层模拟为8节点三维实体单元,建立起管土之间的非线性接触关系.同时,考虑到管材及土体之间的粘结滑移效应,在相互作用模块采用接触对的方法来进行分析,且采用表面与表面接触.接触面之间的相互作用包含2个部分:法向作用和切向作用.切向作用考虑了管土之间的相对滑移,法向行为将管土表面分开的距离称作间隙,只有在压紧状态时才能传递法向压力,在ABAQUS中将这种法向行为称作硬接触.本文法向作用采用硬接触,切向作用采用库伦摩擦模型来传递管土表面的剪应力.此外,由于管材的刚度较大,在选取主控面和从属面时,将接触单元的目标面选取为管道的主控面,而将管材及土体的交界面作为接触单元的从属面.在约束作用方面,选取管壳及土层的边缘,建立起壳-实体耦合的约束类型.跨断层埋地管道平面示意图如图 2所示,采用结构化网络划分技术对管土模型进行划分,网格划分模型如图 3所示.
|
| 图 2 跨断层埋地管道平面示意图(单位:m) Figure 2 Sketch of buried pipeline crossing fault (unit:m) |

|
| 图 3 有限元模型 Figure 3 Finite element model |
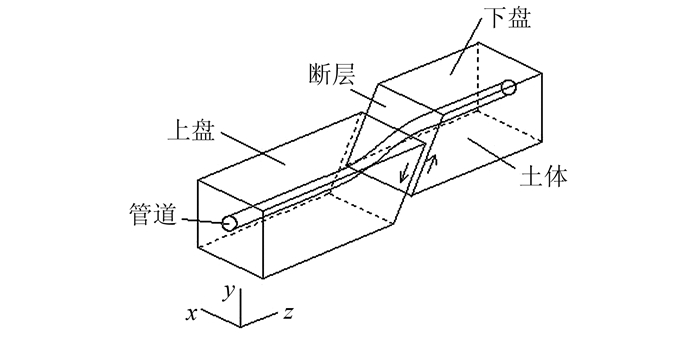
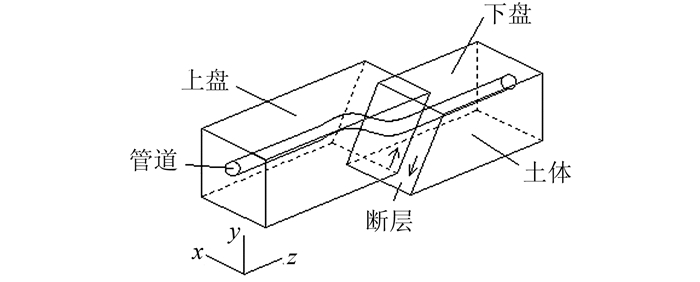
由于本文模拟断层错动的影响是通过在土层边界施加断层位移量来实现的,故边界条件的确定显得尤为重要,确定边界条件首先得了解断层运动的机理,跨断层管道破坏的直接原因是基层上覆土层在断层运动下的变形和破裂上传至地面,从而导致了地面的永久变形.因此,分析跨断层埋地管道,实质上是分析管道在地面永久变形作用下的反应,首先应该确定出模型的边界条件.正、逆断层示意图如图 4、5所示,针对上下、左右及前后6个平面,确定以下边界条件:
|
| 图 4 正断层示意图 Figure 4 Sketch of normal fault |
|
| 图 5 逆断层示意图 Figure 5 Sketch of reverse fault |
1) 由于上表面为地表面,故不施加任何边界条件,使其为自由表面.
2) 对于土体下表面,限制正、逆断层下盘底面3个方向x、y、z的平动,在上盘(断层层面倾斜时,位于断层面上部的土体称为上盘)底面施加相应的位移荷载.
3) 对于正、逆断层,前后及左右边界仅施加x方向的约束.
4) 由于管道与土体建立了表面接触,管道会随着土体运动,同时会发生轴向的滑移,只要管道足够长,管土间的摩擦力足以维持管道的平衡,所以管道可以不设任何约束.
在以上边界条件中,x为管道径向,y为管道的竖直方向,z为管道的轴向.
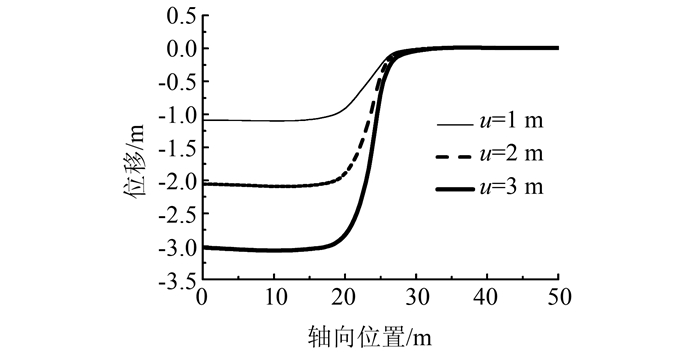
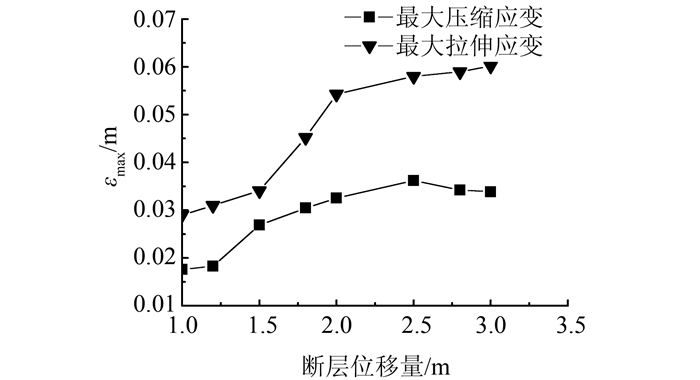
2 数值模拟结果分析 2.1 断层位移的影响图 6表示在砂黏土的均匀场地类型中,选取1.0、1.2、1.5、1.8、2.0、2.5、2.8、3.0 m 8种错层位移,研究不同断层位移对管道形变的影响.在断层位移的作用下,管道沿着断层错动的方向产生变形.随着断层位移的增加,管道的位移和翘曲程度进一步增大,变形曲线的拐点由断层中间向两侧偏移,管道沿着轴向变形的区域不断扩大.图 7表示不同的断层位移对管道最大拉伸应变及最大压缩应变的影响.由图可见,当断层位移量较小时,管道最大拉伸应变曲线比较平缓,应变值相对较小,在断层位移1.5 m处出现应变曲线拐点,此后管道拉伸应变值增长较快,这是由于在断层位移较小时,管道抵抗断层变形及自身塑性变形的能力较强.管道最大压缩应变曲线始终在最大拉伸应变曲线的下方,随着断层位移的增量值先增大后减小,在断层位移为2.5 m时达到峰值,此后应变值逐渐减小.由此可见,在跨断层穿越角为60°时,管道主要的破坏形式为受拉破坏.同时,应当对管道采取适当的构造措施,防止管道的受压破坏.
|
| 图 6 竖直位移沿管轴方向的分布图 Figure 6 Distribution of fault vertical displacement along tube axis |
|
| 图 7 不同断层位移量下的最大应变值 Figure 7 Maximum strain value under different fault displacements |
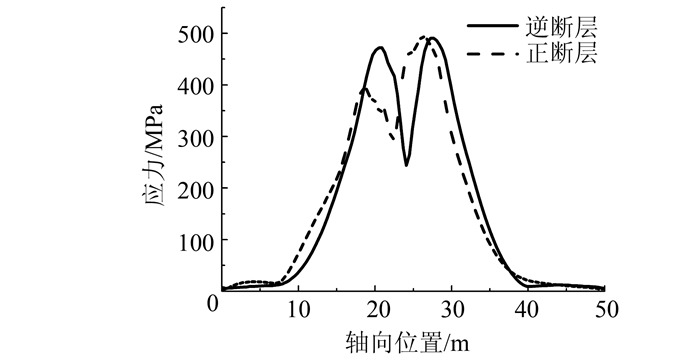
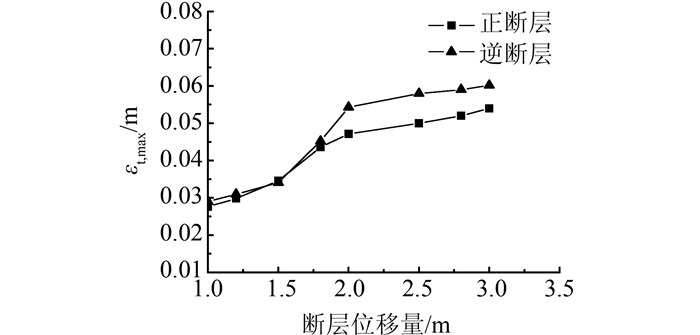
图 8表示在砂黏土的场地类型中,1 m断层位移下,不同正、逆断层对管道应力反应的影响.由图 8可以看到,断层处管道应力(25 m处)较两侧小,主要在断层两侧产生管道应力集中,断层两侧应变值增长较快,埋地管道在正、逆断层中的应力比较接近.管道Mises应力值存在于断层两侧一定范围内,正、逆断层延伸至断层一侧的长度约为20 m,之后管道应力值几乎为0,不再受断层错动影响.图 9表示在砂黏土的均匀场地类型中,选取1.0、1.2、1.5、1.8、2.0、2.5、2.8、3.0 m 8种错层位移,研究在不同的断层类型中,断层位移对管道最大拉伸应变的影响.从图中可以得到,正、逆断层位移作用下的管道,其最大拉伸应变均随着断层位移量的增加而增大,当断层位移小于1.8 m时,埋地管道在正、逆断层中的拉伸应变峰值比较接近,曲线应变增长的比较快.当超过1.8 m后,埋地管道峰值应变在正、逆断层作用下的区别较大,逆断层作用下的应变反应要大于正断层作用下的反应,应变曲线趋于平缓,应变值不断增加,作用位置向断层两侧延伸,断层危险点存在于断层两侧应变较大处.在进行管道研究和设计时,需要考虑不同断层类型对埋地管道受力及变形的影响,特别是在断层位移量相对较大时,不同断层类型对管道的反应不同,断层错动能够引起管段的失效.
|
| 图 8 断层类型对管道Mises应力的影响 Figure 8 Effect of fault type on Mises stress of pipeline |
|
| 图 9 断层类型对管道应变的的影响 Figure 9 Effect of fault type on strain of pipeline |
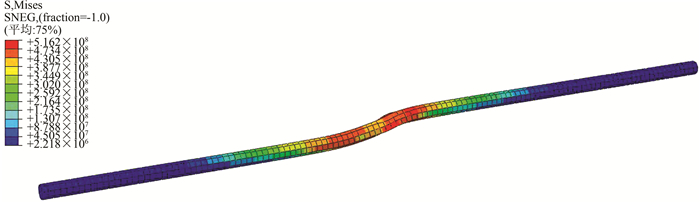
据相关震害资料表明,管道周围的地质条件对管道的受力及变形有较大的影响.由于埋地管道长度较长,在穿越跨断层时难免会穿过不同的场地,管道的受力及变形性能也会随之变化.图 10~13表示在不同场地类型中(非均匀场地为断层左侧砂黏土,右侧石灰岩),正断层1 m错动位移对管道应力应变的影响.从图 10、11中可以看到,管道屈曲破坏主要集中在断层两侧,均匀场地下的管道应力值达到478 MPa,超过X60管道弹性屈服强度.非均匀场地下的管道应力值最大为516 MPa,达到管道塑性屈服强度.图 12、13表示的是不同场地类型对管道应变的影响,非均匀场地的应变值要大于均匀场地的应变值.这是由于管道在穿越跨断层时,断层两侧土层的刚度不同,对管道的约束作用也存在差异.场地的不同致使两侧土层变形不一致,加快了土层塑性变形的进程,管道的变形破坏是最主要的原因.故在研究管道的受力及变形性能时,也应当考虑场地类型这一因素.

|
| 图 10 均匀场地下的管道Mises应力云图 Figure 10 Nephogram of Mises stress of pipeline in uniform field |
|
| 图 11 非均匀场地下的管道Mises应力云图 Figure 11 Nephogram of Mises stress of pipeline in nonuniform field |

|
| 图 12 均匀场地下的管道最大主应变云图 Figure 12 Miximum principal strain of pipeline in uniform field |

|
| 图 13 非均匀场地下的管道最大主应变云图 Figure 13 Maximum principal strain of pipeline in nonuniform field |
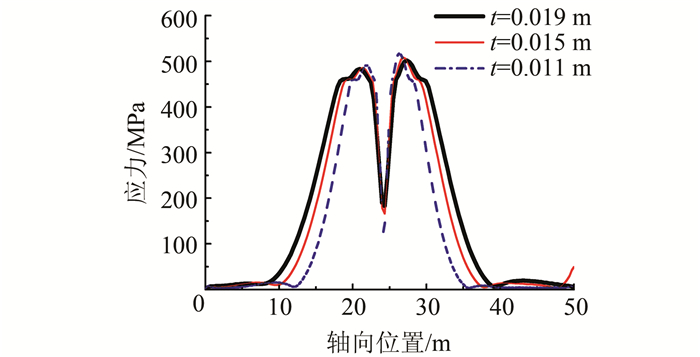
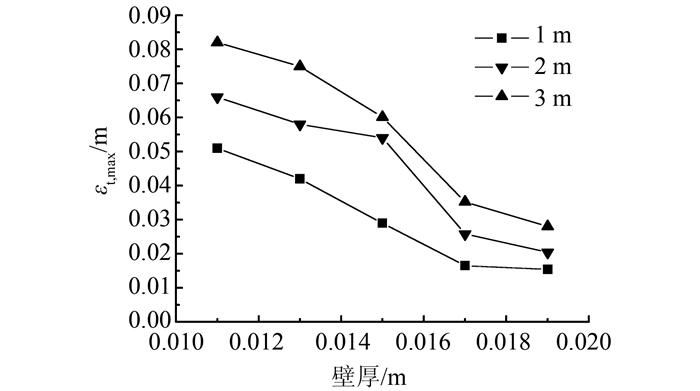
本文选取了0.011、0.013、0.015、0.017、0.019 m共5个管壁厚度进行模拟.图 14表示在1 m断层位移下,选取0.011、0.015、0.019 m的3个管道壁厚,研究管道壁厚对管道Mises应力的影响.从图中可以观察到,随着壁厚的增加,管道的应力反应逐渐减小.图 15表示在不同的断层位移下,管道应变反应随壁厚的变化情况.随着管道壁厚的增加,管道的横截面面积也在逐渐增大,管道的刚度随之增大,抵抗断层错动及管道自身塑性变形能力不断变强,最大拉伸应变值逐渐减小.故在对管道进行抗震设计时,适当增加管道的壁厚,有利于增强管道的抗震性能.
|
| 图 14 壁厚对管道Mises应力的影响 Figure 14 Effect of pipeline thickness on Mises stress |
|
| 图 15 壁厚对管道应变的的影响 Figure 15 Effect of pipeline thickness on strain of pipeline |
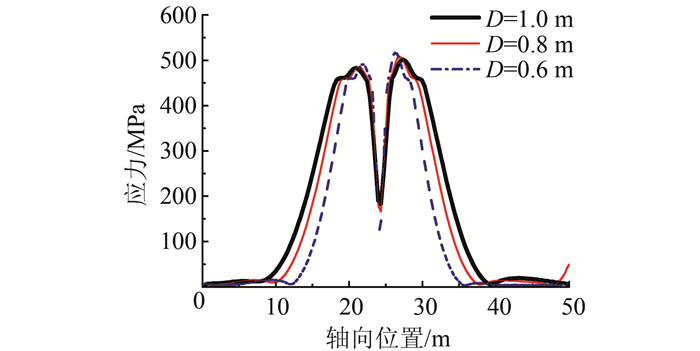
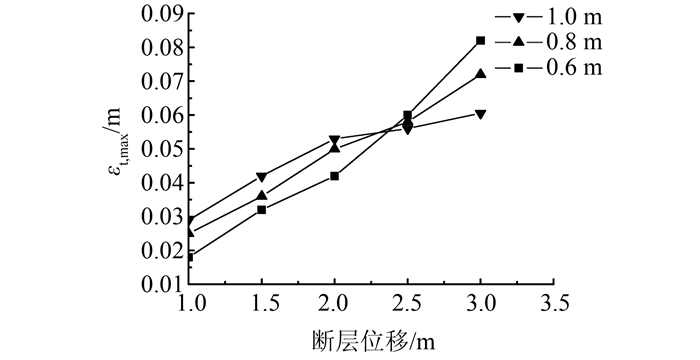
本文选取了0.6、0.8、1.0 m3个管径进行模拟.图 16表示在1 m断层位移下,管径对管道Mises应力的影响.从图中可以得到,随着管径的增加,管道的应力反应逐渐增大.图 17表示在不同的管径下,管道应变反应随管径的变化情况.由图可得,当断层位移在2.2 m左右时,管道最大拉伸应变值随着管径的增加逐渐增大,当断层位移超过2.2 m时,管道应变反应随着管径的增加逐渐减小.这是由于在断层位移较小时,跨断层土体对管道约束刚度增大的影响小于管道刚度增大的影响.当断层位移较大时,外径增加导致土体对管道约束刚度增大的影响大于管道刚度增大的影响.故在管道壁厚一定时,尽量选择管径较小的埋地管道穿越跨断层,防止管道受到破坏.
|
| 图 16 管径对管道Mises应力的的影响 Figure 16 Effect of pipeline diameter on Mises stress |
|
| 图 17 管径对管道应变的的影响 Figure 17 Effect of pipeline diameter on strain of pipeline |
本文采用了管土之间非线性接触的有限元分析模型,通过对断层表面施加位移荷载,采用拟静力的方法对管道受力与变形性能进行了分析,得到以下结论.
1) 随着断层位移的增加,管道在竖直方向的位移加大,管道主要的破坏形态为受拉破坏.
2) 断层位移较大时,埋地管道峰值应变在正逆断层作用下的区别较大,逆断层作用下的应变反应要大于正断层作用下的应变反应.
3) 场地的不同导致两侧土层变形不一致,加快了土层塑性变形的进程,管道的变形破坏是最主要的原因.
4) 随着壁厚的增加,管道的刚度增大,管道的应力应变反应逐渐减小.
5) 断层位移较小时,选取管径较小的埋地管道能够减轻管道的破坏.
| [1] | Newmark N M. Seismic design criteria for structures and facilities of tans-Alaska pipeline system[C]// Proceedings U. S. National Conference on Earthquake Engineering, Ann Arbor, Michigan: EERT, 1975: 94-103. |
| [2] | Kennedy R P, Chow A W, Williamson R A. Fault movement effects on buried oil pipeline[J]. Journal of Transp Engineering, ASCE, 1977, 103: 617–633. |
| [3] | Wang L R L, Yeh Y H. A refined seismic analysis and design of buried pipeline for fault movement[J]. Earthquake Engineering and Structural Dynamics, 1985, 13: 75–96. DOI:10.1002/(ISSN)1096-9845 |
| [4] | Takada S, Hassani N, Fukuda K. Damage directive in buried pipelines at Strike-slip fault crossings[J]. SoilDynamics and Earthquake Engineering, 2006, 27: 200–211. |
| [5] |
慕园, 余志峰, 刘玉卿. 埋地管道通过逆断层的有限元分析[J].
石油机械, 2015, 43(10): 112–115.
Mu Yuan, Yu Zhifeng, Liu Yuqing. Strength analysis of buried gas pipeline in reverse fault[J]. China Petroleum Machinery, 2015, 43(10): 112–115. |
| [6] |
刘铭刚, 杨秀娟, 闫相祯, 等. 基于多重非线性管—土耦合模型的管道应变设计方法[J].
中国测试, 2016, 42(7): 9–14.
Liu Minggang, Yang Xiujuan, Yan Xiangzhen, et al. Strain design analysis method of buried pipeline based on multiple nonlinear pipe-soil coupling model[J]. China Measurement & Test, 2016, 42(7): 9–14. DOI:10.11857/j.issn.1674-5124.2016.07.002 |
| [7] |
刘啸奔, 张宏, 李勐, 等. 断层作用下埋地管道应变分析方法研究进展[J].
油气储运, 2016, 35(8): 799–807.
Liu Xiaoben, Zhang Hong, Li Meng, et al. Research progress of strain analysis methods for buried pipelines under faulting process[J]. Oil & Gas Storage and Transportation, 2016, 35(8): 799–807. |
| [8] |
冯启民, 赵林. 跨越断层埋地管道屈曲分析[J].
地震工程与工程振动, 2001, 21(4): 80–87.
Feng Qimin, Zhao Lin. Buckling analysis of buried pipes subjected to fault movements[J]. Earthquake Engineering and Engineering Vibration, 2001, 21(4): 80–87. |
| [9] |
王滨, 李昕, 周晶. 地震断层作用下的埋地管道等效分析模型[J].
防灾减灾工程学报, 2009, 29(1): 44–49.
Wang Bin, Li Xin, Zhou Jin. Equivalent analysis model of buried pipeline under seismic fault[J]. Journal of Disaster Prevention and Mitigation Engineering, 2009, 29(1): 44–49. |
| [10] |
范锋, 丰晓红. 跨断层埋地输气管道有限元模型建立与分析[J].
油气储运, 2014, 33(1): 11–15.
Fan Feng, Feng Xiaohong. Establishment and analysis of finite element model of buried gas pipeline crossing fault[J]. Oil & Gas Storage and Transportation, 2014, 33(1): 11–15. |
| [11] |
丰晓红, 刘武, 范锋. 跨断层埋地输气管道应变计算方法研究[J].
油气储运, 2014, 32(3): 1–4.
Feng Xiaohong, Liu Wu, Fan Feng. Study on the method of calculating the strain of buried gas pipeline crossing fault[J]. Oil & Gas Storage and Transportation, 2014, 32(3): 1–4. |
| [12] |
马骅, 冯启民, 高泽涛, 等. GB50470-2008油气输送管道线路工程抗震技术规范[S]. 北京: 中国计划出版社, 2008: 49-50.
Ma Hua, Feng Qimin, Gao Zetao, et al. GB50470-2008 Seismic Technical Code for Oil and Gas Transmission Pipeline Engineering[S]. Beijing: China Planning Press, 2008: 49-50. |
 2017, Vol. 50
2017, Vol. 50




