文章信息
- 黄伟军, 余敏, 李易
- HUANG Weijun, YU Min, LI Yi
- 钢筋混凝土梁板结构的抗火性能有限元分析
- Finite element analysis of fire-resistance of reinforced concrete beam and slab structures
- 武汉大学学报(工学版), 2017, 50(6): 867-873
- Engineering Journal of Wuhan University, 2017, 50(6): 867-873
- http://dx.doi.org/10.14188/j.1671-8844.2017-06-011
-
文章历史
- 收稿日期: 2017-06-16
2. 北京工业大学城市与工程安全减灾教育部重点实验室, 北京 100124
2. Key Laboratory of Urban Security and Disaster Reduction Engineering of Ministry of Education, Beijing University of Technology, Beijing 100124, China
建筑火灾的频繁发生给人们的生命财产和资源环境造成严重危害[1].钢筋混凝土结构由于取材广泛、易于施工、造价低等优点,被广泛地应用于各种建筑结构,其遭受火灾的程度也更为严重,是火灾研究的主要对象.
钢筋混凝土梁和板作为混凝土结构最基本的组成单元,其在火灾下的高温力学性能研究具有重要意义.早在20世纪80年代,国外学者Gustaferro等[2]就提出了多种受火工况下钢筋混凝土梁耐火极限确定的方法,计算结果与试验数据吻合较好.Ellingwood等[3]、EI-Hawary等[4]对火灾下钢筋混凝土简支梁的抗弯和抗剪性能开展了试验研究,总结了梁受弯和受剪破坏规律.Kudor等[5]建立了考虑混凝土热爆裂现象的温度场计算、热应力分析的计算模型,并模拟了钢筋混凝土简支/连续梁热-力耦合全过程,与足尺试验结果进行比较,两者吻合较好.时旭东等[6]通过6根钢筋混凝土2跨连续梁的高温试验,考察了不同加载位置、持荷水平及单双跨加温等因素下连续梁变形和内力变化规律.吴波等[7]考察了荷载比、跨高比、配筋率和混凝土保护层厚度对简支梁耐火极限的影响,给出了普通/高强混凝土简支梁耐火极限的简化计算方法;张威振等[8]采用有限元方法分析了高温后足尺钢筋混凝土梁的力学性能和变形反应;丁发兴等[9]对2根钢筋混凝土梁进行高温试验研究及有限元分析,探讨了保护层厚度及荷载水平对钢筋混凝土简支梁抗火性能的影响.Usmani等[10-12]对Cardington试验的组合楼板进行温度场和力学性能分析,温度场分析采用二维平面,力学性能分析采用分层壳单元,较好地模拟了结构的材料非线性和几何非线性.陈礼刚等[13]对足尺钢筋混凝土简支板、3跨连续板进行了恒载下的受火试验,研究了钢筋混凝土连续板在高温下的变形、温度分布规律.王滨等[14]进行了2块四边简支钢筋混凝土双向板足尺试件的火灾试验,研究了沿板厚温度场分布和板的变形规律.唐贵和等[15]采用ABAQUS有限元软件分析了高跨比、保护层、荷载比、钢筋屈服强度、混凝土的抗压强度和抗拉强度等参数对钢筋混凝土双向板耐火性能的影响.整体结构耐火性能的研究相对较少.杨志年等[16, 17]利用自行研制的火灾试验炉,对足尺整体结构中钢筋混凝土双向板的耐火性能进行了试验研究;陈适才等[18]利用分层壳单元和纤维梁单元对混凝土框架的整体耐火行为进行了分析,结果表明楼板对结构整体耐火性能影响较大;李易等[19-21]基于纤维梁模型和分层壳模型开发了混凝土框架火灾倒塌分析程序,采用有限元方法对火灾下整体框架结构倒塌过程和机理进行分析.
在此,采用分层壳建立了钢筋混凝土梁、板及梁板结构的高温热力耦合计算模型,并对梁板结构的耐火性能进行进行了试验验证.在此基础上,分析并比较了钢筋混凝土梁板整体结构与单个梁、板构件的耐火性能.
1 钢筋混凝土梁板耐火有限元模型高温时,钢材和混凝土因其内部物理参数的变化从而表现出不同的力学性能,为进行高温下钢筋混凝土结构的有限元分析,必须确定钢筋和混凝土的结构模型参数.在钢筋混凝土结构的耐火计算中,需要用到高温下钢筋和混凝土的热工参数和高温力学本构.
1.1 材料热工参数温度场的计算是构件抗火计算的第1步,分析时忽略钢筋的影响,温度场分析中混凝土的热工参数主要包括:密度、导热系数和比热.混凝土的密度不随温度变化,保持为2 350 kg/m3.导热系数和比热均采用欧洲规范Eurcode 2[22]提供的数据.
1.2 材料高温本构钢筋采用双折线本构模型,切线模型为弹性模量的0.01倍,屈服准则为Von Mises屈服准则.高温下的弹性模型和屈服强度随温度的升高而减小,各参数随温度的取值均采用EC2[22]建议的数据.
混凝土采用混凝土塑性损伤模型,高温下混凝土应力-应变本构关系及热膨胀系数见文献[22].
1.3 温度场计算模型火灾下钢筋混凝土内部的传热按傅里叶传热理论,混凝土表面与外界通过热对流和热辐射交换能量,即
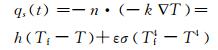 (1)
(1)
式中:h为对流换热系数,受火面h=25 W/(m2·K),背火面h=8 W/(m2·K);ε为辐射换热系数,在受火面和背火面分别取0.7和0;σ为玻尔兹曼常数,σ=5.67×10-8W/(m2·K4);Tf为标准火灾升温曲线.
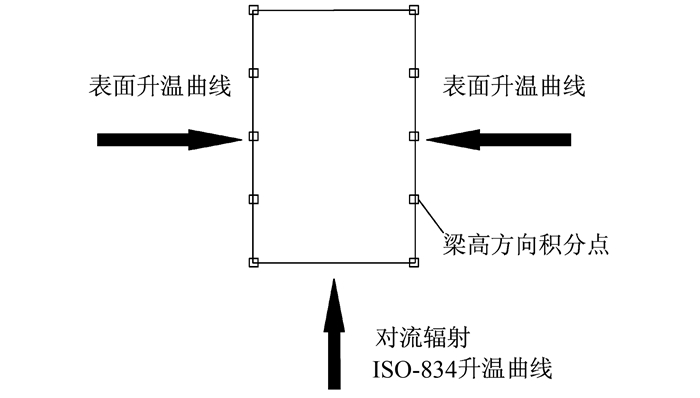
钢筋混凝土楼板底面受火,受火面按照ISO-834标准升温曲线进行升温;钢筋混凝土梁3面均匀受火,火灾环境温度采用ISO834标准升温曲线,背火面采用绝热边界条件,其受火情况如图 1所示.梁采用壳单元建模时,其侧面的温度边界条件通过积分点直接施加升温曲线,该曲线由相应尺寸梁的二维模型温度场分析获得.
|
| 图 1 钢筋混凝土梁受火条件示意图 Figure 1 Fire condition of reinforced concrete beam |
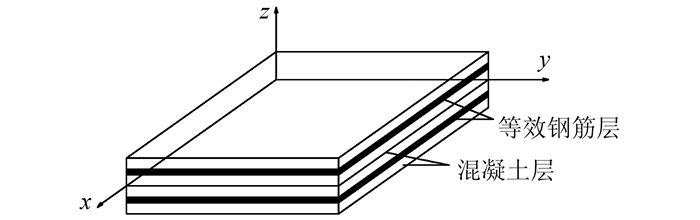
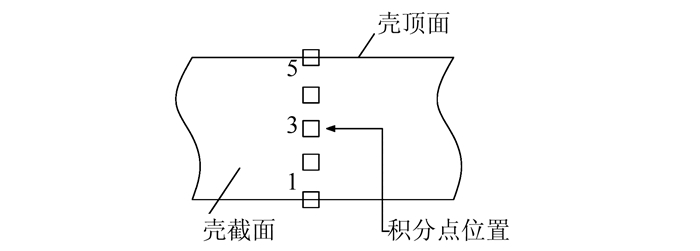
钢筋混凝土楼板有限元模型一般有2种类型:离散式三维实体单元和分层壳单元.其中实体单元精细化建模,尽管具有较高的计算精度,但建模过程复杂,且单元数量多,计算效率低,因此不适于结构整体分析.分层壳单元是将混凝土沿厚度方向分为若干层,同时将钢筋网弥散为钢筋层参加截面的力学性能计算,如图 2所示.这种模型相对简单,并且具有较好的精度,单元数目相对实体单元要少得多,适合于结构整体分析.壳单元的积分点沿厚度方向均匀分布,如图 3所示.
|
| 图 2 分层壳单元示意图 Figure 2 Element of layered shell |
|
| 图 3 壳厚度方向的积分点分布图 Figure 3 Distribution of integral points along thickness of shell |
钢筋混凝土梁也采用上述分层壳单元,其中梁纵向通长钢筋可以按图 4所示的2种方式设置:1)按照刚度和面积的等效方式弥散为钢筋层;2)将梁的横截面沿着梁的宽度方向划分为不同的单元,然后沿壳单元厚度方向分层,在划分出的小截面上将纵向钢筋弥散为钢筋层.方式2将截面进行划分,使混凝土与钢筋分离开,这样的方式虽然更接近于实际状况,但建模时较复杂,不适于大规模结构整体分析.因此本文中,钢筋混凝土梁壳单元中钢筋均按照第1种方式插入.
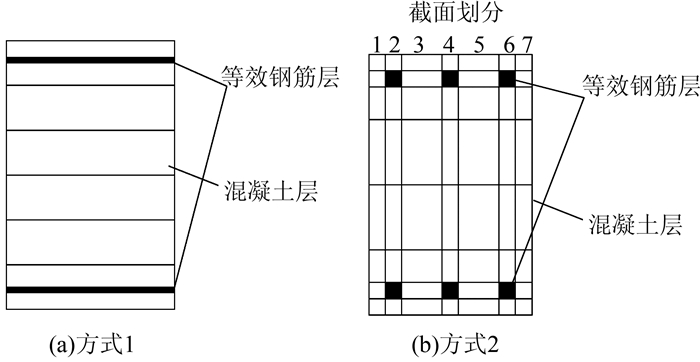
|
| 图 4 壳单元中的钢筋嵌入示意图 Figure 4 Embedding method of steel bar in shell element |
对于高温下的热-力耦合计算,本文中的混凝土采用分层壳单元(S4RT),每层沿截面厚度方向上采用5个积分点的Simpson积分;钢筋采用等效钢筋层的方式嵌入到混凝土单元中.混凝土截面的温度由相应的积分点读取,钢筋的温度通过插值来获得.该单元能够考虑结构几何非线性和材料非线性,更好地模拟轴压-平面内弯曲-平面内剪切-平面外弯曲之间的耦合作用.
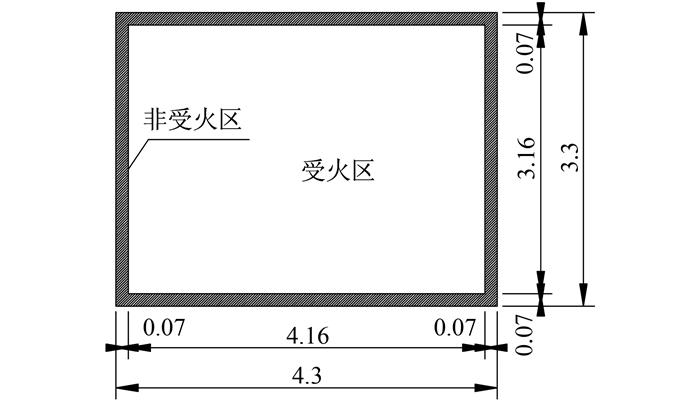
2 有限元模型的试验验证 2.1 钢筋混凝土单块板的耐火试验验证为验证上述有限元模型在钢筋混凝土板耐火性能计算上的适用性,在此选择文献[23, 24]中的HD12板的耐火试验作为验证对象.耐火试验试件HD12的几何尺寸及有限元模型如图 5、6所示.
|
| 图 5 钢筋混凝土板(单位:m) Figure 5 Reinforced concrete slab (unit:m) |

|
| 图 6 钢筋混凝土板耐火模型 Figure 6 Fire resistance model of reinforced concrete slab |
试件HD12板的基本信息如下:尺寸为4.3 m×3.3 m,边界非受火区宽度为0.07 m; 板厚度为100 mm,板底铺设钢筋网,钢筋直径12 mm,间距200 mm;钢筋屈服强度为468 MPa,保护层厚度为25 mm;混凝土的强度为36.7 MPa;板自重荷载2.4 kPa,板上均布荷载为3.0 kPa,总荷载5.4 kPa;边界条件为4边简支;耐火试验时间3 h.
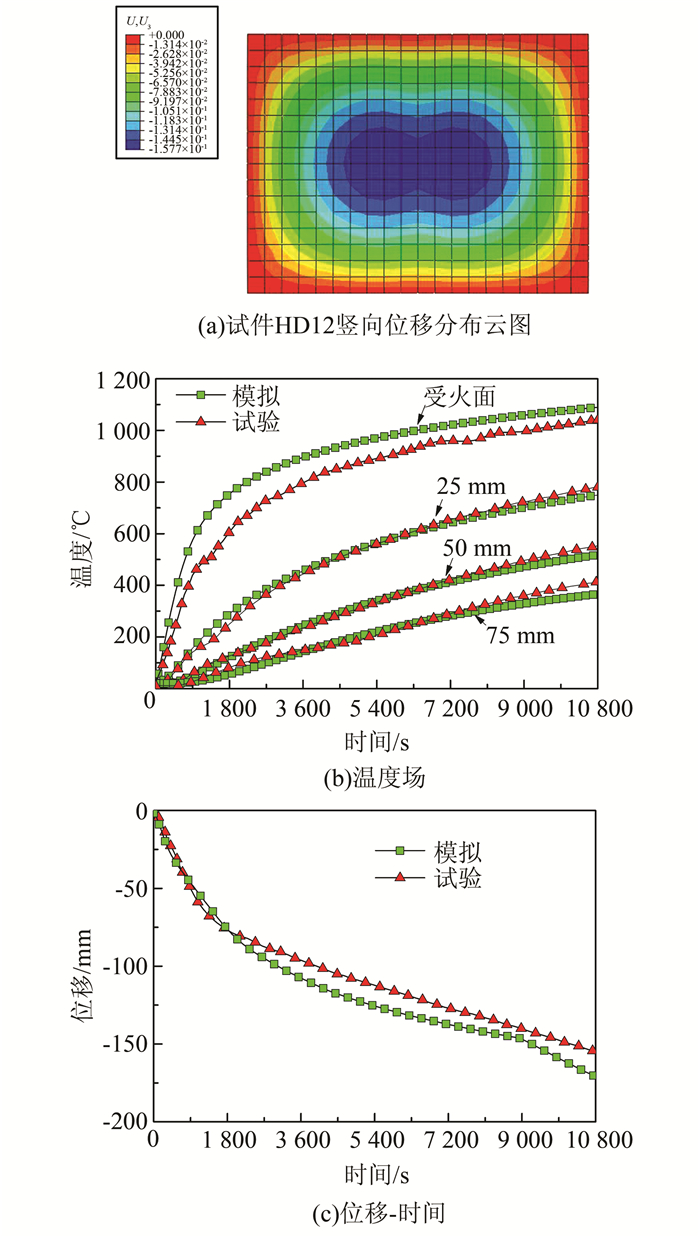
通过上述有限元模型可以计算得到的温度及板跨中位移随耐火时间的变化曲线,有限元计算结果和试验数据对比如图 7所示.从图中可以看出:计算结果与试验结果吻合较好.
|
| 图 7 钢筋混凝土板有限元与试验结果的比较 Figure 7 Comparison of fire resistance of reinforced concrete slab between FEA and experiment |
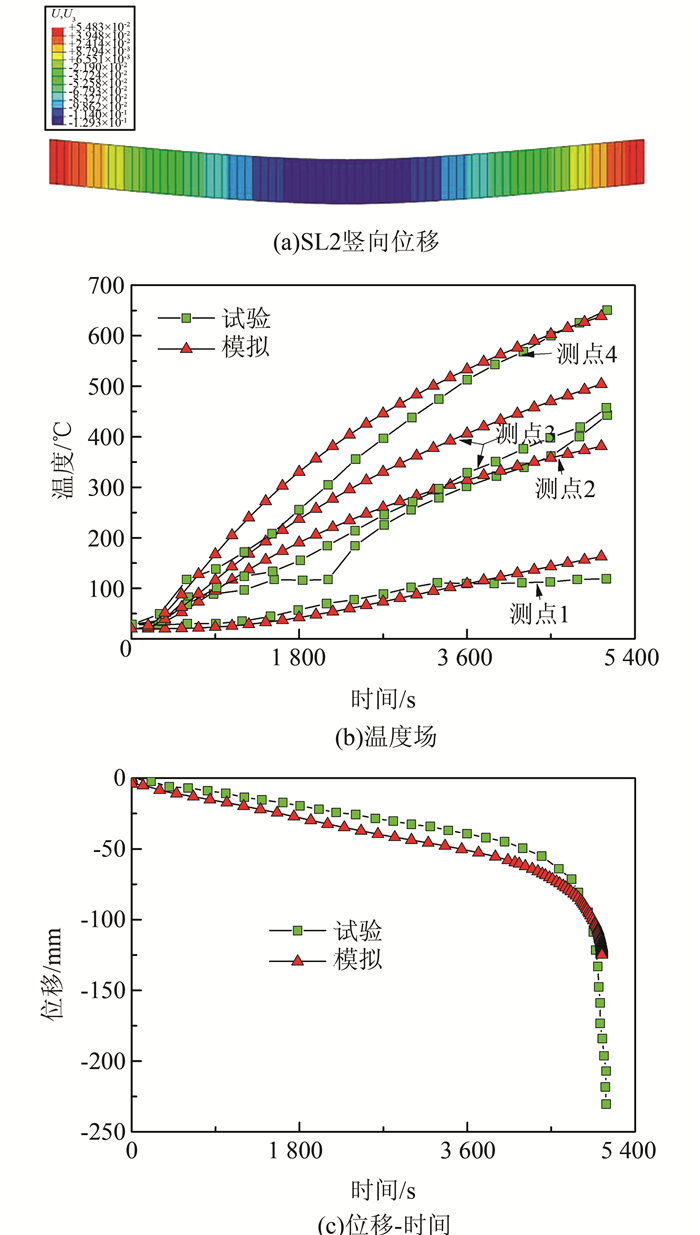
为验证上述有限元模型在钢筋混凝土梁以及钢筋混凝土梁板体系耐火性能计算上的适用性,在此选择文献[25]中的3个耐火试验进行模拟,耐火构件的试验结果和构件详细尺寸及配筋情况见文献[25].3根构件测点温度和跨中位置曲线的对比结果见图 8~10.

|
| 图 8 梁构件SL1有限元和试验结果比较 Figure 8 Comparison of fire resistance of reinforced concrete beam SL1 between FEA and experiment |
|
| 图 9 梁构件SL2有限元和试验结果比较 Figure 9 Comparison of fire resistance of reinforced concrete beam SL2 between FEA and experiment |
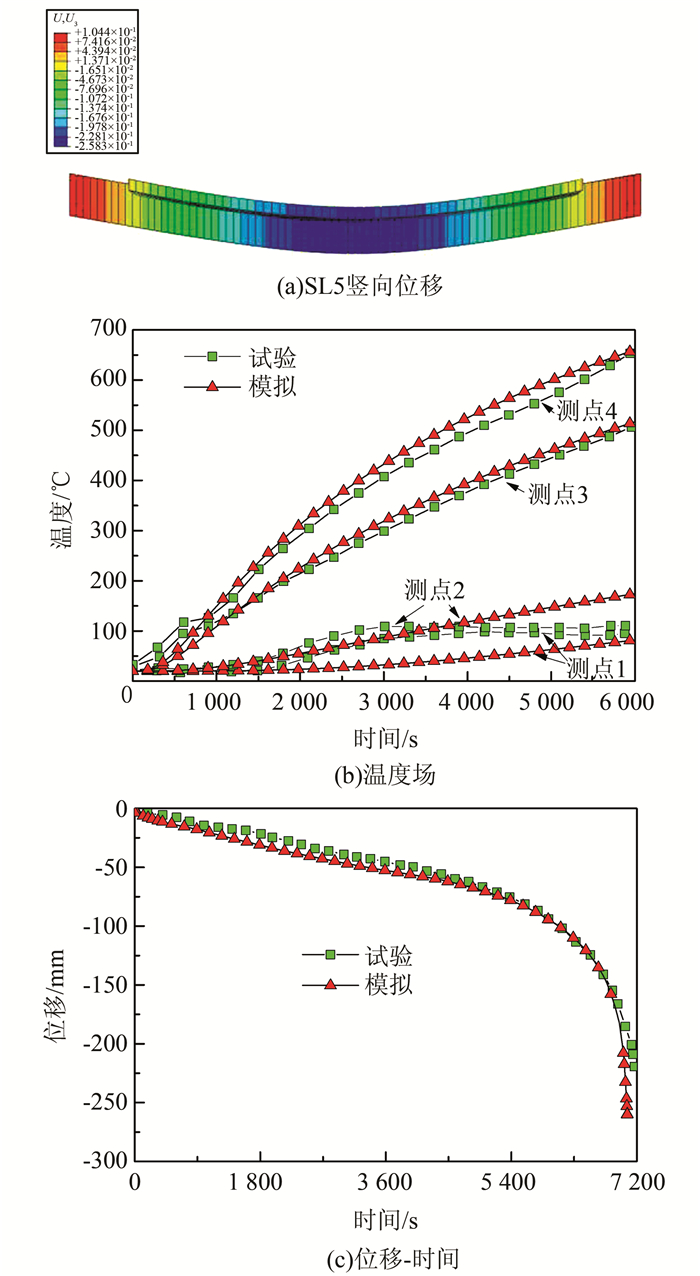
|
| 图 10 梁板构件SL5有限元和试验结果比较 Figure 10 Comparison of fire resistance of reinforced concrete beam SL5 between FEA and experiment |
通过上面的对比,可以看出温度曲线吻合良好,跨中位移对于构件SL1前期吻合良好,后期有一定的差别,但是最终的耐火极限时间非常接近.对于构件SL2,跨中位移曲线和试验结果吻合良好.
对于梁板体系,由上面的对比可知,升温曲线和跨中位移曲线都和试验吻合良好.通过上面的试验验证,证明本文采用的分层壳计算模型可以很好地对单块楼板、单根梁以及板梁体系进行耐火模拟.
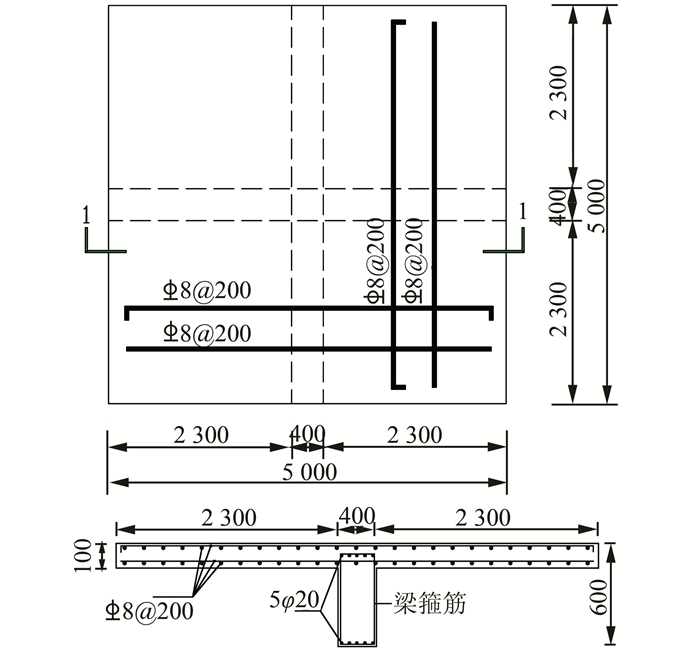
3 钢筋混凝土梁板结构耐火性能分析为分析钢筋混凝土梁板整体结构与单个梁、板构件耐火性能的差异性,以及混凝土的热膨胀和构件端部约束条件对钢筋混凝土结构耐火性能的影响,设计出以下算例:混凝土强度等级取C30,钢筋采用HRB335,钢筋混凝土板配有上下双层双向钢筋

|
| 图 11 钢筋混凝土梁板结构 Figure 11 Reinforced concrete beam and slab structure |
|
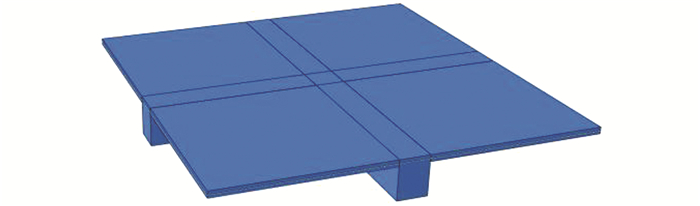
| 图 12 钢筋混凝土梁板体系有限元模型 Figure 12 Finite element model of reinforced concrete beam and slab structure |
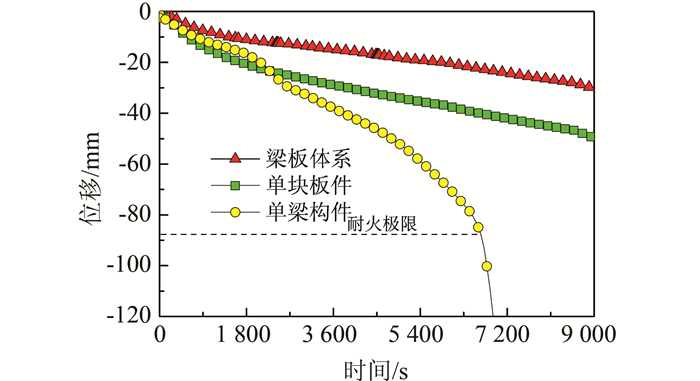
对上述梁板体系及其中对称的单个梁、板构件进行有限元分析,结构或构件均为简支边界条件.图 13所示为梁板体系、单块板件以及单梁构件最大竖向位移随时间的变化图.
|
| 图 13 梁板体系与单个构件的耐火比较 Figure 13 Comparison of the fire resistance between whole structure and single component |
从图上结果可知,梁板体系在耐火计算时间为2.5 h时的极限变形值为30.3 mm,而相同条件下单块板构件的极限变形值为49.6 mm,单梁构件的耐火极限为1.85 h,此时构件的变形速率超过其极限弯曲变形速率[26].由于结构整体性的影响,梁板间的刚度和承载力均互有增强,并且有相邻跨的约束和负弯矩作用,使得整体结构中的受火跨变形减小.
3.2 混凝土热膨胀影响图 14所示为梁板体系和单个构件位移-时间曲线在考虑混凝土膨胀和不考虑膨胀情况下的变化,边界条件均为简支.从图中可以看出:混凝土的热膨胀对结构的耐火性能有不利影响,由于混凝土的热膨胀影响,钢筋混凝土结构在高温条件下的变形会大大增加,而且耐火极限时间缩短.
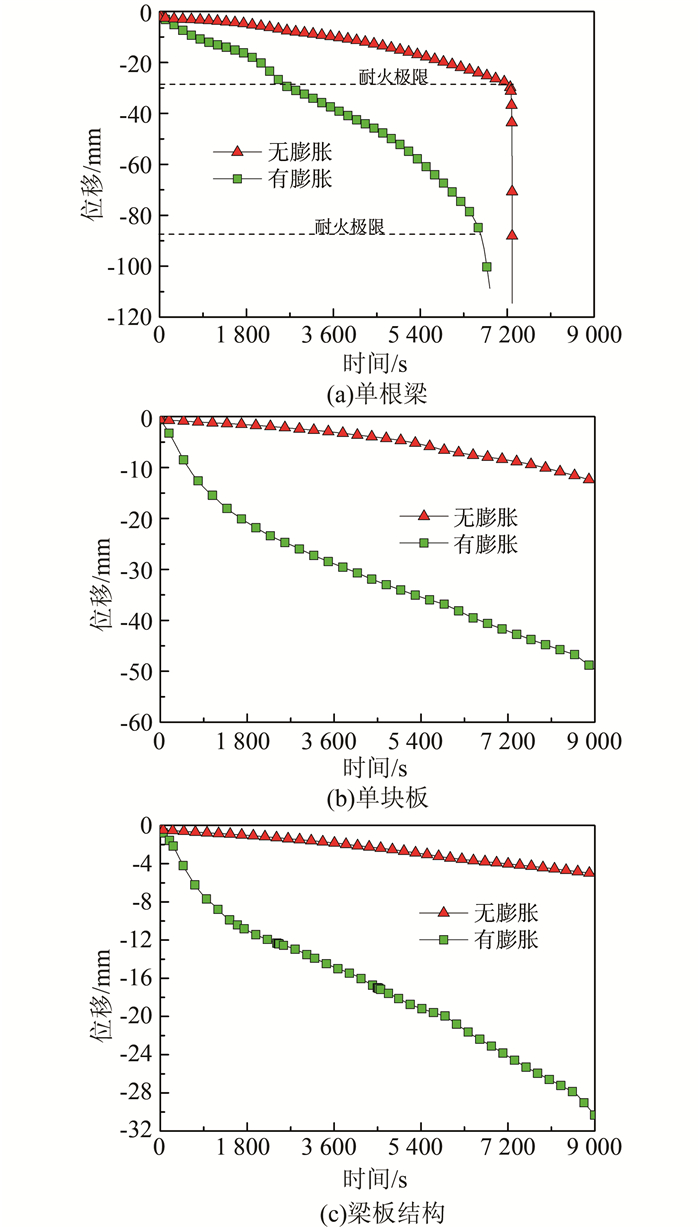
|
| 图 14 混凝土热膨胀对梁、板及梁板耐火性能的影响 Figure 14 Effect of thermal expansion on fire resistance of reinforced concrete structures |
采用有限元软件分析了梁板体系、单个板件和单梁构件在简支和固支等不同约束条件下的耐火性能.从图 15可以看出:固支边界构件的竖向位移比简支边界的小得多,随着约束刚度的增大,竖向挠度明显减小,构件的耐火性能在一定程度上得到提高.
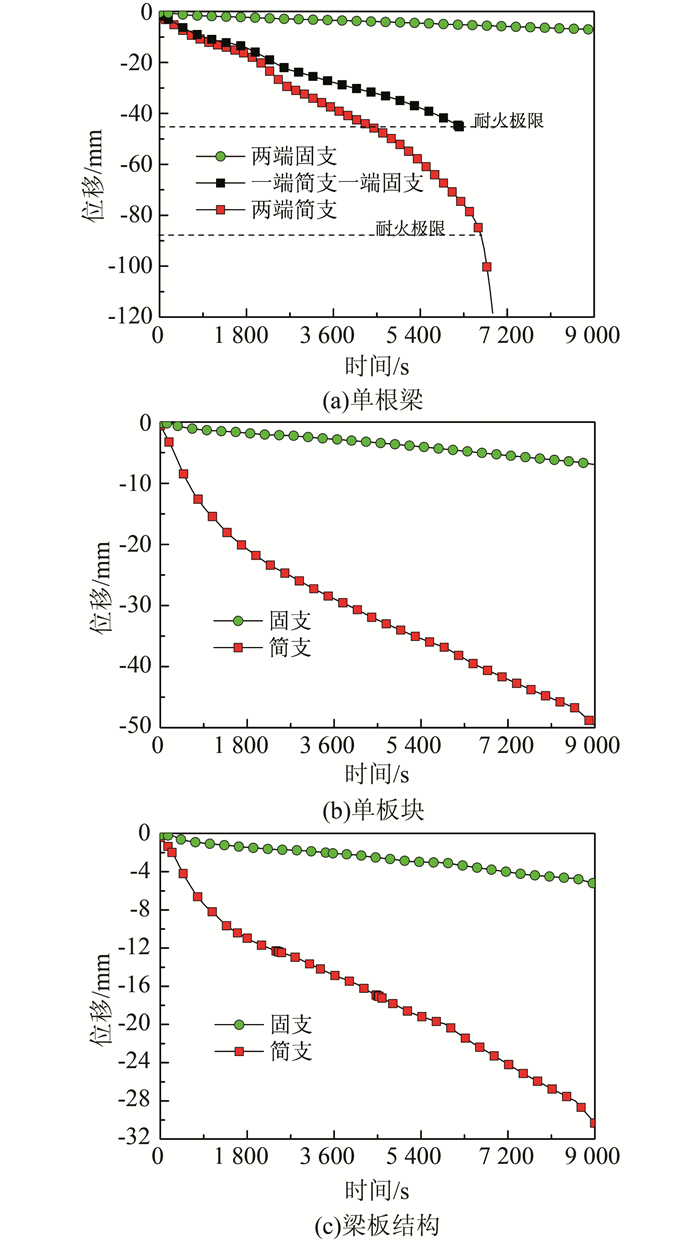
|
| 图 15 不同约束条件对梁、板及梁板耐火性能的影响 Figure 15 Effects of different boundary conditions on fire resistance of reinforced concrete structures |
1) 采用分层壳模型可以很好地分析模拟梁、板及梁板体系结构在火灾高温下的变形特征及耐火极限,计算得到的温度场及变形结果均与试验吻合良好,表明本文建立的完全的热力耦合模型的有效性.
2) 混凝土的热膨胀对火灾下的钢筋混凝土变形有明显影响,但是对简支构件的耐火极限影响较小.
3) 不同的约束条件下结构或构件的耐火性能不同,约束体系的刚度越大,构件的竖向变形越小,使混凝土结构或构件的耐火性能有所提高.
4) 梁板结构体系中,梁板间的连接和约束对构件的耐火性能有所加强,使整体结构的耐火变形减小.
| [1] |
郑文忠, 侯晓萌, 王英. 混凝土及预应力混凝土结构抗火研究现状与展望[J].
哈尔滨工业大学学报, 2016(12): 1–18.
Zheng Wenzhong, Hou Xiaomeng, Wang Ying. Progress and prospect of fire resistance of reinforced concrete and prestressed concrete structures[J]. Journal of Harbin Institute of Technology, 2016(12): 1–18. DOI:10.11918/j.issn.0367-6234.2016.12.001 |
| [2] | Gustaferro A H, Lin T D. Rational design of reinforced concrete members for fire resistance[J]. Fire Safety Journal, 1986, 11(1-2): 85–98. DOI:10.1016/0379-7112(86)90054-8 |
| [3] | Ellingwood B, Lin T D. Flexure and shear behavior of concrete beams during fires[J]. Journal of Structural Engineering, 1991, 117(2): 440–458. DOI:10.1061/(ASCE)0733-9445(1991)117:2(440) |
| [4] | El-Hawary M, Ragab A, Elazim A. Effect of fire on flexural behaviour of RC beams[J]. Construction and Building Materials, 1996, 10(2): 147–150. DOI:10.1016/0950-0618(95)00041-0 |
| [5] | Kodur V K R, Dwaikat M. A numerical model for predicting the fire resistance of reinforced concrete beams[J]. Cement & Concrete Composites, 2008, 30(5): 431–443. |
| [6] |
时旭东, 过镇海. 高温下钢筋混凝土连续梁的受力性能试验研究[J].
土木工程学报, 1997(4): 26–34.
Shi Xudong, Guo Zhenhai. Experimental investigation of behavior of reinforced concrete continuous beams at elevated temperature[J]. China Civil Engineering Journal, 1997(4): 26–34. |
| [7] |
吴波, 洪洲. 钢筋混凝土简支梁的耐火极限[J].
华南理工大学学报(自然科学版), 2006(7): 82–87.
Wu Bo, Hong Zhou. Fire resistance of simply supported reinforced concrete beam[J]. Journal of South China University of Technology(Natural Science Edition), 2006(7): 82–87. |
| [8] |
张威振. 足尺钢筋混凝土简支梁高温力学性能的试验研究[J].
工业建筑, 2007(4): 37–41.
Zhang Weizhen. Experimental investigation on the mechanical performance of full-scale simple reinforced concrete beams under and after elevated temperature[J]. Industrial Construction, 2007(4): 37–41. |
| [9] |
丁发兴, 姚飞, 李喆, 等. 高温下钢筋混凝土简支梁的抗火性能[J].
东北大学学报(自然科学版), 2015(10): 1476–1481.
Ding Faxing, Yao Fei, Li Zhe, et al. Fire resistance of simple supported reinforced concrete beams under high temperature[J]. Journal of Northeastern University (Natural Science), 2015(10): 1476–1481. DOI:10.3969/j.issn.1005-3026.2015.10.024 |
| [10] | Usmani A S, Cameron N. Limit capacity of laterally restrained reinforced concrete floor slabs in fire[J]. Cement & Concrete Composites, 2004, 26(2): 127–140. |
| [11] | Huang Z H, Burgess I W, Plank R J. Effective stiffness modelling of composite concrete slabs in fire[J]. Engineering Structures, 2000, 22(9): 1133–1144. DOI:10.1016/S0141-0296(99)00062-0 |
| [12] | Huang Z H, Burgess I W, Plank R J. Fire resistance of composite floors subject to compartment fires[J]. Journal of Constructional Steel Research, 2004, 60(2): 339–360. DOI:10.1016/j.jcsr.2003.08.012 |
| [13] |
陈礼刚. 钢筋混凝土板受火性能的试验研究[D]. 西安: 西安建筑科技大学, 2004.
Chen Ligang. The experiment research of reinforced concrete slab[D]. Xi'an: Xi'an University of Architecture and Technology, 2004. http://d.wanfangdata.com.cn/Thesis/Y616544 |
| [14] |
王滨, 董毓利. 四边简支钢筋混凝土双向板火灾试验研究[J].
建筑结构学报, 2009, 30(6): 23–33.
Wang Bin, Dong Yuli. Experimental research of four-edge simple support two-way reinforced concrete slab under fire[J]. Journal of Building Structures, 2009, 30(6): 23–33. |
| [15] |
唐贵和, 黄金林. 钢筋混凝土双向板耐火性能研究[J].
中南大学学报(自然科学版), 2012, 43(7): 2827–2832.
Tang Guihe, Huang Jinlin. Fire resistance of two-way reinforced concrete slab[J]. Journal of Central South University, 2012, 43(7): 2827–2832. |
| [16] |
杨志年, 董毓利, 吕俊利, 等. 整体结构中钢筋混凝土双向板火灾试验研究[J].
建筑结构学报, 2012, 33(9): 96–103.
Yang Zhinian, Dong Yuli, Lu Junli, et al. Experimental study of two-way reinforced concrete slab subjected to fire in a whole structure[J]. Journal of Building Structures, 2012, 33(9): 96–103. |
| [17] |
杨志年, 董毓利. 钢框架结构中钢筋混凝土双向板火灾试验研究[J].
工程力学, 2013(4): 337–344.
Yang Zhinian, Dong Yuli. Experimental study of two-way reinforced concrete slab subjected to fire in a steel-framed building[J]. Engineering Mechanics, 2013(4): 337–344. |
| [18] |
陈适才, 任爱珠, 陆新征. 火灾下空间混凝土框架结构的反应分析与模拟[J].
自然灾害学报, 2007(6): 88–92.
Chen Shicai, Ren Aizhu, Lu Xinzheng. Numerical analysis and simulation of space concrete frames under fire[J]. Journal of Natural Disasters, 2007(6): 88–92. |
| [19] |
李易, 陆新征, 任爱珠, 等. 某八层混凝土框架结构火灾连续倒塌模拟[J].
工程力学, 2011(S1): 53–59.
Li Yi, Lu Xinzheng, Ren Aizhu, et al. Simulation for fire-induced progressive collapse of an 8-storey RC frame structure[J]. Engineering Mechanics, 2011(S1): 53–59. |
| [20] |
李易, 陆新征, 叶列平, 等. 混凝土框架结构火灾连续倒塌数值分析模型[J].
工程力学, 2012(4): 96–103.
Li Yi, Lu Xinzheng, Ye Lieping, et al. Numerical models of fire induced progressive collapse analysis for reinforced concrete frame structures[J]. Engineering Mechanics, 2012(4): 96–103. DOI:10.6052/j.issn.1000-4750.2010.06.0397 |
| [21] | Li Y, Lu X, Guan H. A case study on a fire-induced collapse accident of a reinforced concrete frame-supported masonry structure[J]. Fire Technology, 2016, 52(3): 707–729. DOI:10.1007/s10694-015-0491-0 |
| [22] | European Committee for Standardization. BS EN 1992-1-2: 2004. Design of Concrete Structures: Part 1-2: General Rules-Structural Fire Design[S]. Brussels, 2004. |
| [23] | Wade C, Lim L. Experimental fire tests of two-way concrete slabs[R]. Fire Engineering Research Report, New Zealand: University of Canterbury, 2002. |
| [24] | Lim L, Buchanan A, Moss P. Numerical modelling of two-way reinforced concrete slabs in fire[J]. Engineering Structures, 2004, 26(8): 1081–1091. DOI:10.1016/j.engstruct.2004.03.009 |
| [25] |
唐贵和. 钢筋混凝土T形梁及梁-板组合体的耐火性能研究[D]. 广州: 华南理工大学, 2014.
Tang Guihe. Fire performance of reinforced concrete T-beams and beam-slab assemblies[D]. Guangzhou: South China University of Technology, 2014. |
| [26] |
中国国家标准化管理委员会. GB/T9978-2008建筑构件耐火试验方法第一部分: 通用要求[S]. 北京: 中国标准出版社, 2008.
Standardization Administration of the People's Republic of China. GB/T9978-2008 Fire-Resistance Tests-Elements of Building Construction—Part 1: General Requirements [S]. Beijing: Standards Press of China, 2008. |
 2017, Vol. 50
2017, Vol. 50




