文章信息
- 傅佳宏, 田铭兴, 高云波
- FU Jiahong, TIAN Mingxing, GAO Yunbo
- 基于深度优先搜索的混合补偿网络拓扑辨识与分析
- Identification and analysis of hybrid compensation network topology based on depth-first search algorithm
- 武汉大学学报(工学版), 2019, 52(4): 344-350
- Engineering Journal of Wuhan University, 2019, 52(4): 344-350
- http://dx.doi.org/10.14188/j.1671-8844.2019-04-010
-
文章历史
- 收稿日期: 2018-11-12
2. 兰州交通大学甘肃省轨道交通电气自动化工程实验室,甘肃 兰州 730070
2. Rail Transit Electrical Automation Engineering Laboratory of Gansu Province, Lanzhou Jiaotong University, Lanzhou 730070, China
近年来,高速铁路和城市轨道交通的快速发展,越来越多的非线性、大容量负载接入电力系统.谐波污染治理与无功补偿成为电力系统和电力用户亟需解决的问题[1-3].混合补偿系统作为一种谐波、无功和负序综合补偿装置,因其容量大、成本低、补偿效果好等优点受到广泛的关注.混合补偿系统发展呈多样化的趋势,各种不同的混合补偿系统相继被研发出来[4-8].为此研究人员对多种不同拓扑的混合补偿系统进行了归纳和比较分析[9-11].这些研究表明,混合补偿系统补偿网络的拓扑决定着混合补偿系统的有源元件的容量、性能和成本等关键指标,因此对混合补偿系统补偿网络的拓扑进行研究至关重要.
文献[12]以对偶原理为基础,对混合型有源滤波器的补偿网络拓扑进行了辨识,但分析基于已知拓扑,辨识方法不全面.文献[13]将补偿网络看作由端子和补偿元件组成的网络对混合补偿系统拓扑进行了详尽的分析,但未提出严格的辨识方法,且辨识采用手工方式,客观性低、分析范围有限.
针对上述问题,本文基于深度优先搜索算法,提出一种混合补偿系统补偿网络的计算机辨识和分析新方法.该方法首先根据图论建立补偿网络的邻接矩阵模型,并根据节点和支路的连接规则得到所有可能的补偿网络的邻接矩阵的生成方法;之后根据电气连接的有效性给出补偿网络的辨识条件,并基于深度优先搜索算法辨识出电气连接有效的邻接矩阵;改进邻接矩阵,使其能准确地描述混合补偿系统补偿网络的拓扑,同时给出改进的邻接矩阵的生成方法;最后,分析程序辨识出的2元件混合补偿系统补偿网络的拓扑,并与文献[13]的结果相比较,证明本文方法的正确性和有效性,较现有研究在拓扑辨识方面更加全面.
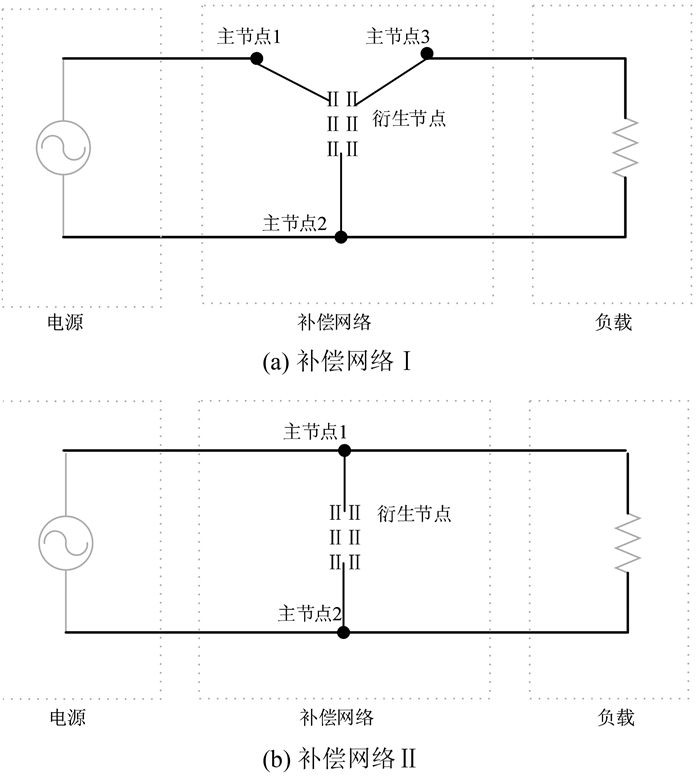
1 混合补偿系统的单相等效电路混合补偿系统的单相等效电路的一般形式如图 1所示,其有2种形式,分别如图 1(a)、(b)所示.
|
| 图 1 混合补偿系统单相等效电路的一般形式 Fig. 1 General forms of equivalent circuit of hybrid compensation system |
图 1中,补偿网络由m个补偿元件连接而成.补偿网络拓扑有n个节点,其中,与电源或者与负载连接的点称为主节点,如图 1(a)中节点1、2和3,以及图 1(b)中节点1和2,其他节点称为衍生节点.
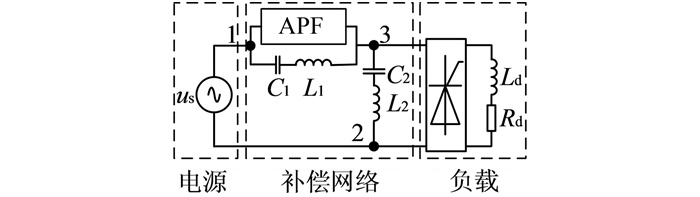
以文献[6]所提的一种串联混合APF为例,其单相等效电路示意图如图 2所示.
|
| 图 2 串联混合APF单相等效电路示意图 Fig. 2 Equivalent circuit of series hybrid active power filter |
假设APF为元件1,C1和L1组成无源滤波器PF1为元件2,C2和L2组成的无源滤波器PF2为元件3.可以得知,补偿网络中的节点1、2和3为主节点.
2 混合补偿网络邻接矩阵及其生成 2.1 补偿网络的邻接矩阵模型具有n个节点的邻接矩阵A是一个n维对称矩阵,用来描述图中支路和节点之间的连接关系.当节点i和j之间存在支路时aij=1,否则aij=0.
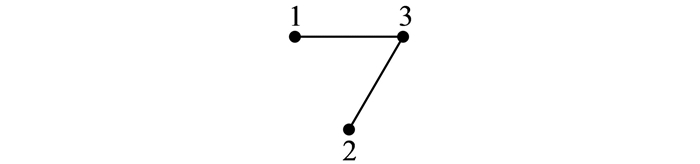
图 2所示的串联混合APF的补偿网络有3个节点和3个元件,将APF和PF2的并联组合看作一条支路, 得到的补偿网络的图如图 3所示.
根据邻接矩阵的定义,其对应邻接矩阵模型如下:
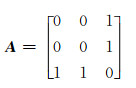 (1)
(1)
若把元件的并联组合看作1条支路,则补偿网络的图中支路数l和元件数m的关系是
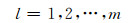 (2)
(2)
当l条支路组成一个完全图时,图的节点最少,此时l=nl(nl-1)/2.所以对于图 1(a),节点数n与支路数l的关系是
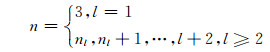 (3)
(3)
对于图 1(b),节点数n与支路数l的关系是
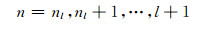 (4)
(4)
式中:
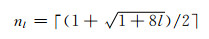
由于图 1(a)、(b)的分析方法相同,本文只针对图 1(a)进行阐述.
2.3 混合补偿网络邻接矩阵的生成对于一个n维邻接矩阵A,由于其主对角线元素为0,且为对称矩阵,所以当确定了元素aij(i=2, 3, …,n;j=1, 2, …, i-1)是等于1还是等于0,就确定了该邻接矩阵.对于n个节点l条支路的图,这样的元素aij的个数为n(n-1)/2,其中有l个元素为1,其余元素为0.因此,本文提出n个节点l条支路所有邻接矩阵的生成方法如下.
从小到大依次取1到2n(n-1)/2-1中的自然数,并将其转换成n(n-1)/2位二进制数,如果该二进制数中1的个数是l个,则把该二进制数看作一个n(n-1)/2维行向量(其元素记作b),那么:
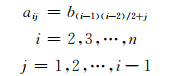 (5)
(5)
例如,当节点数为3、支路数为2时,1到7的7个自然数对应的3位二进制数依次是:001、010、011、100、101、110、111,其中,1的个数是2的二进制数是:011、101和110.把这3个二进制数分别看作3个3维行向量,则根据式(5)可得到如下3个邻接矩阵:
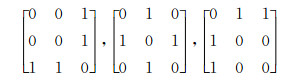
所以,根据式(2)、(3)以及上述n个节点l条支路所有邻接矩阵的生成方法,生成m个元件的所有邻接矩阵的流程图如图 4所示.
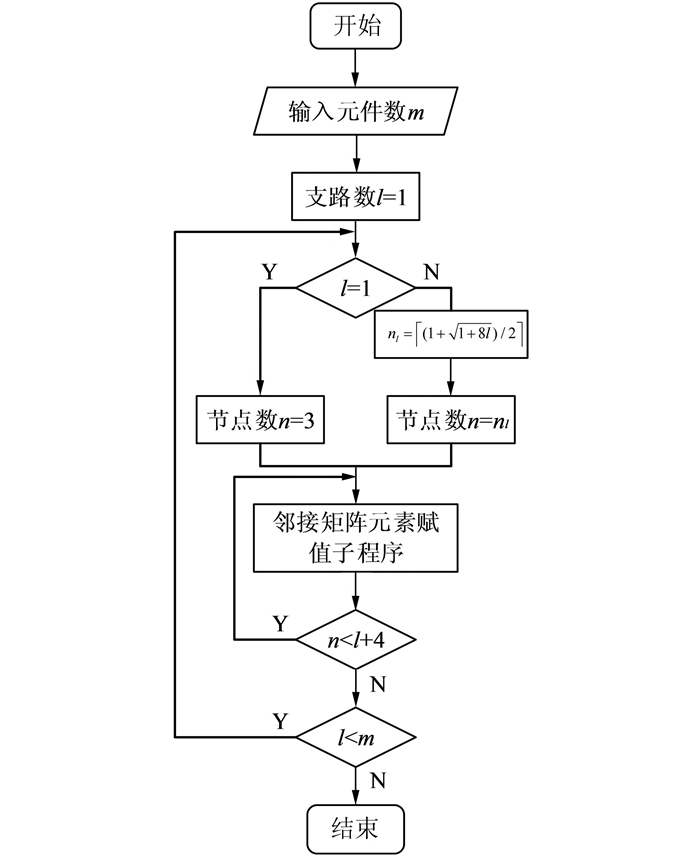
|
| 图 4 邻接矩阵生成流程图 Fig. 4 Flowchart of generation of adjacency matrix |
由第2节所述方法得到的邻接矩阵,可能存在孤立节点和同构.另外,对于一个电气连接有效的补偿网络还应满足以下2个约束条件.
1) 约束条件1:电源和负载之间不允许断路,因此对于图 1(a)主节点1和3之间至少存在1条通路,且当节点1和3之间有且仅有1条通路时,该通路不经过主节点2.
2) 约束条件2:考虑到补偿元件的成本较高,混合补偿系统中的所有元件均被使用,元件的任意一端都不能悬空.因此, 所有的元件都是主节点通路中的一部分.
因此,为了得到电气连接有效的邻接矩阵,需要对第2节所述方法得到的邻接矩阵所生成的图进行辨识.
1) 进行邻接矩阵是否存在孤立节点和同构的辨识.如果存在除主节点2以外的孤立节点和同构,则舍去该邻接矩阵.其基本思想是:如果一个邻接矩阵的某行某列元素都为0,则该邻接矩阵生成的图存在孤立节点;如果一个邻接矩阵在保持对称性的前提下任意交换2行2列后和另一个邻接矩阵相同,则这2个邻接矩阵生成的图同构[14].
2) 进行邻接矩阵是否满足约束条件1和约束条件2的辨识.如果不满足约束条件1和约束条件2,则舍去该邻接矩阵.由此,得到的邻接矩阵的辨识流程图如图 5所示.
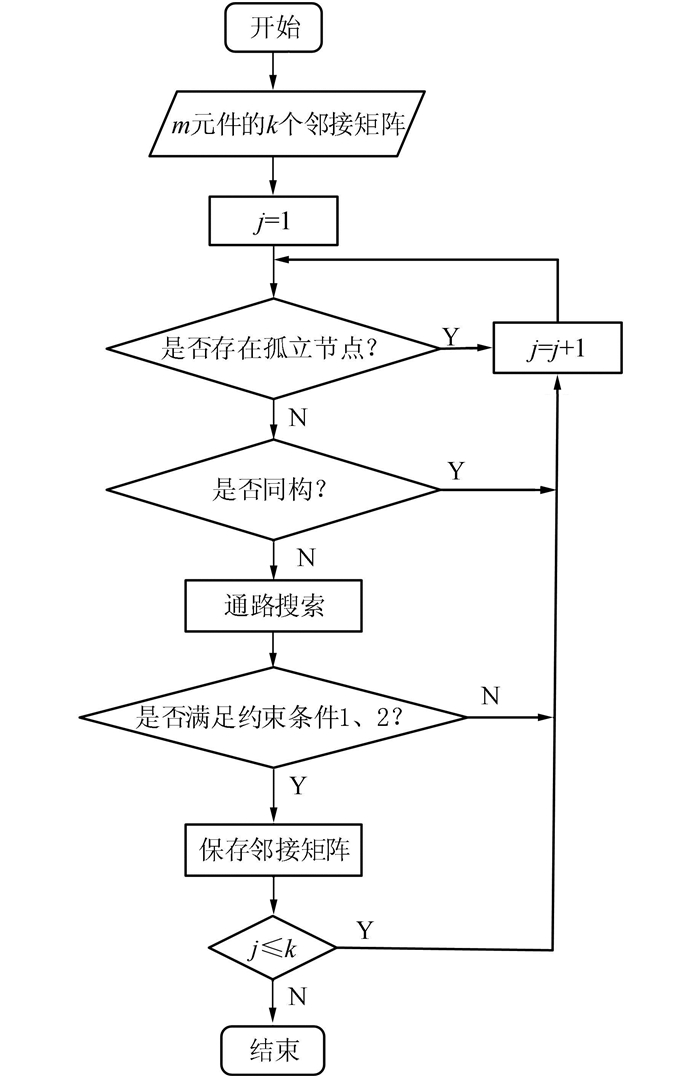
|
| 图 5 邻接矩阵生成图的辨识流程图 Fig. 5 Flowchart of identification of adjacency matrix |
由3.1节可知,进行邻接矩阵是否满足约束条件1和约束条件2的判断,其核心工作是进行通路搜索.本文采用深度优先搜索算法对两节点之间的通路进行搜索[14, 15].
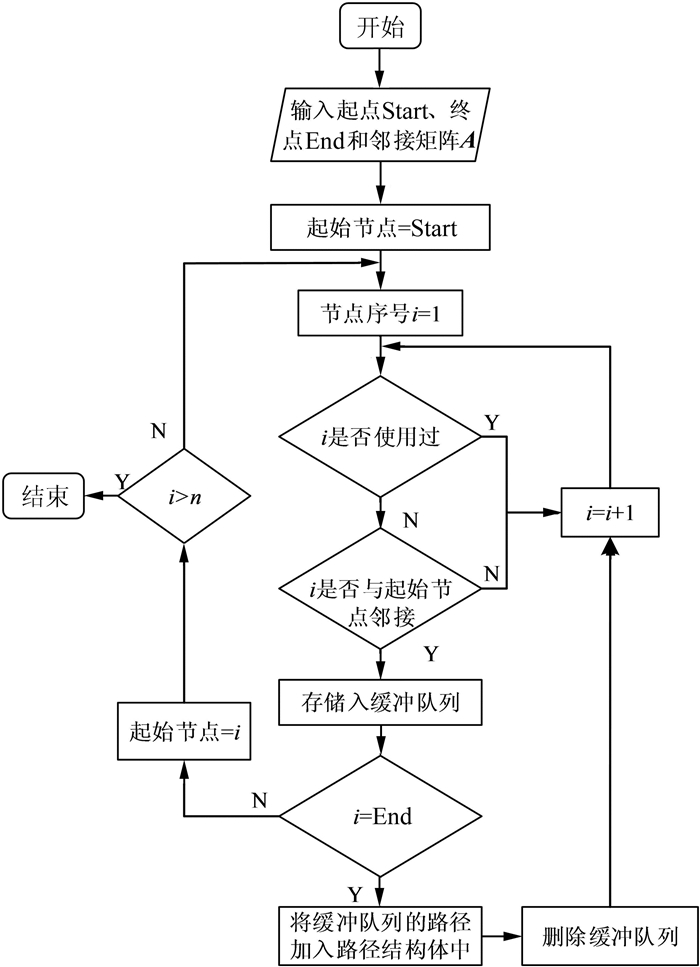
基于深度优先搜索的通路搜索流程如图 6所示.程序由起点开始搜索,若搜索到未被使用且与起始节点相邻接的节点,对节点进行进一步判断:
|
| 图 6 深度优先算法流程图 Fig. 6 Flowchart of depth-first search algorithm |
1) 若该节点是终点,则输出该路径到通路结构体,且回溯到起始节点.
2) 若节点不是终点,且在该条路径中未被使用过,将该节点设为起始节点.
根据这2个递归条件进行搜索,直至遍历所有的节点.
4 邻接矩阵的改进及生成 4.1 改进的邻接矩阵由第2节可知,邻接矩阵A仅能表示补偿网络的拓扑中任意2个节点之间是否存在支路,无法反映支路中有哪几个元件并联.为了使邻接矩阵A能够反映支路中并联元件的信息,需要对邻接矩阵进行改进.
改进的邻接矩阵T的元素tij是由一个二进制数转化而来的十进制数.该二进制数按如下方法得到:若节点i与j之间存在第k(1≤k≤m)个元件,则该二进制数的第k+1位为1,否则为0.
以图 2所示的混合补偿系统补偿网络为例.节点1、3之间并联元件1和元件2,因此其二进制数为0110,对应的十进制数为6;节点1、2之间只有一个元件3,因此其二进制数为1000,对应的十进制数为8.改进的邻接矩阵如下式所示:
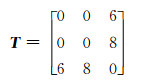 (6)
(6)
由以上分析可以看出,改进的邻接矩阵T和邻接矩阵A一样,是一个主对角元素为0的n维对称矩阵.因此,对于m个元件n个节点l条支路的图,需要确定改进的邻接矩阵T的元素有n(n-1)/2,其中的l个元素不等于0,其他元素等于0,且其不等于0的元素的位置与邻接矩阵中元素等于1的位置相同,并满足:
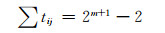
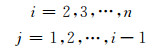 (7)
(7)
因此,改进的邻接矩阵T的确定方法如下:
令邻接矩阵A中l个等于1的元素(实际上有2l个,但由于矩阵对称,只需确定l个元素)分别任意取2到2m+1-4中一个偶数,若这l个偶数相加等于2m+1-2,且这l个偶数的m+1位的二进制数的1的个数相加等于m,则此时的A就是改进的邻接矩阵T,其元素必然满足式(7).
以3个补偿元件、邻接矩阵如式(1)的补偿网络为例.显然A是一个3维对称矩阵,其中有2×2=4个元素等于1,因此改进的邻接矩阵T需要确定的元素只有2个(t31、t32或t13、t23).
令t31和t32任取2到12中的一个偶数,当t31=2(0010B)、t32=12(1100B),t31=4(0100B)、t32=10(1010B),t31=6(0110B)、t32=8(1000B),t31=8(1000B)、t32=6(0110B),t31=10(1010B)、t32=4(0100B),t31=12(1100B)、t32=2(0010B)时,满足t31+t32=14,且t31、t32的二进制数中1的个数相加为3,因此得到的改进邻接矩阵为
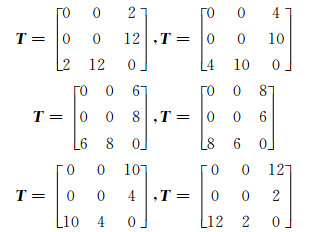
由此得到改进的邻接矩阵生成程序如图 7所示.
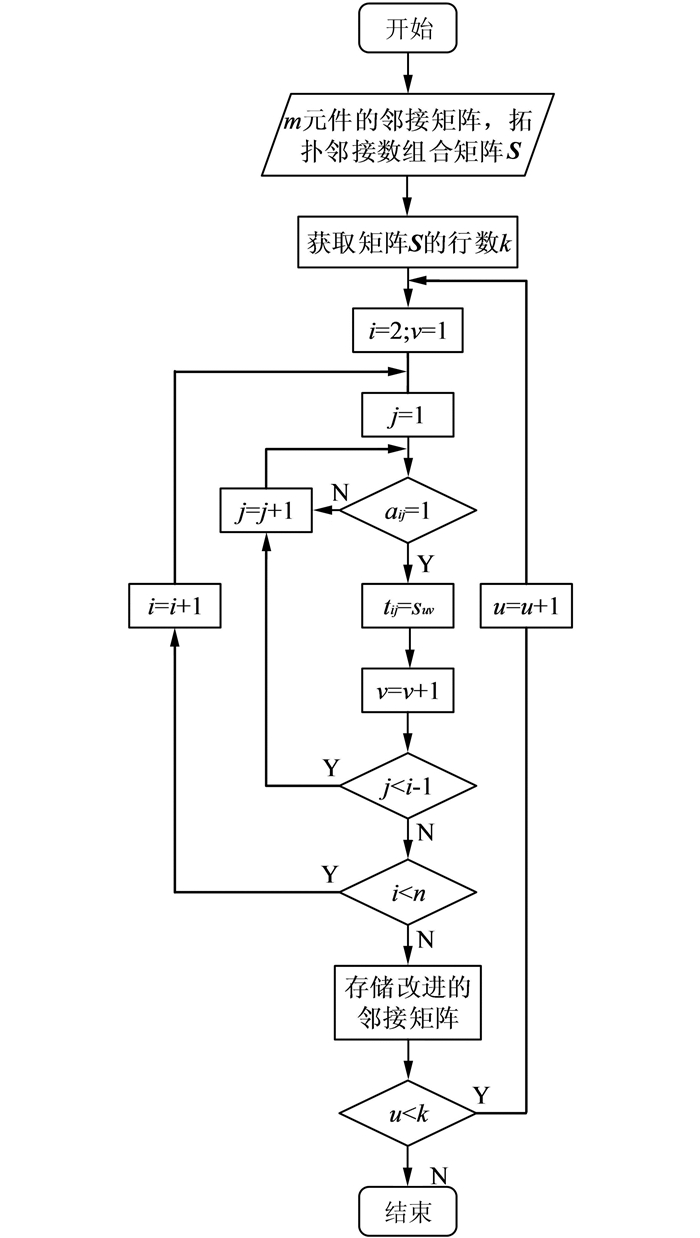
|
| 图 7 改进邻接矩阵生成流程图 Fig. 7 Flowchart of generation of novel adjacency matrix |
综合上述分析,可以得到混合补偿网络拓扑辨识流程如图 8所示.
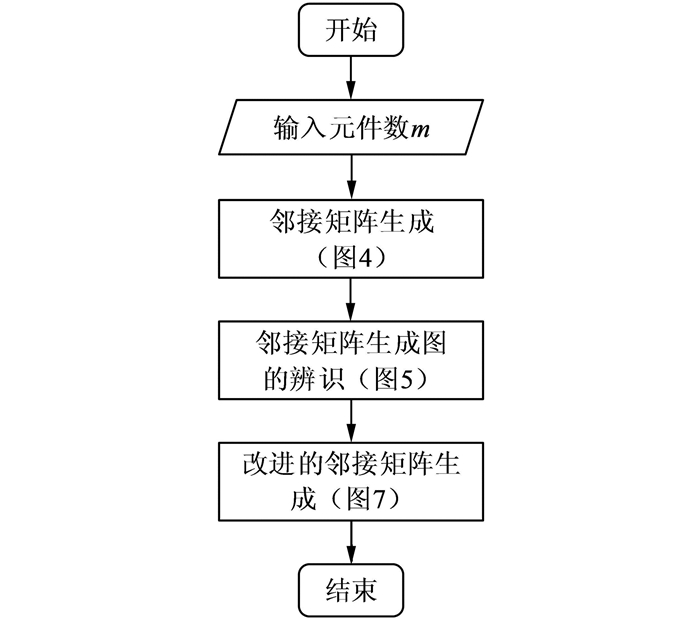
|
| 图 8 混合补偿网络拓扑辨识流程图 Fig. 8 Flowchart of topology identification of hybrid compensation network |
根据图 8所示流程图,很容易编写出混合补偿网络拓扑的辨识程序,完成m元件的补偿网络拓扑的自动辨识.
5 方法验证及算例分析 5.1 方法正确性验证采用所编写的辨识程序,假设补偿网络是由2个元件构成,则针对图 1(a)生成的改进的邻接矩阵及其拓扑图有7个,而针对图 1(b)生成的改进的邻接矩阵及其拓扑图有3个,如图 9所示.其中,白色元件代表元件1,黑色元件代表元件2.
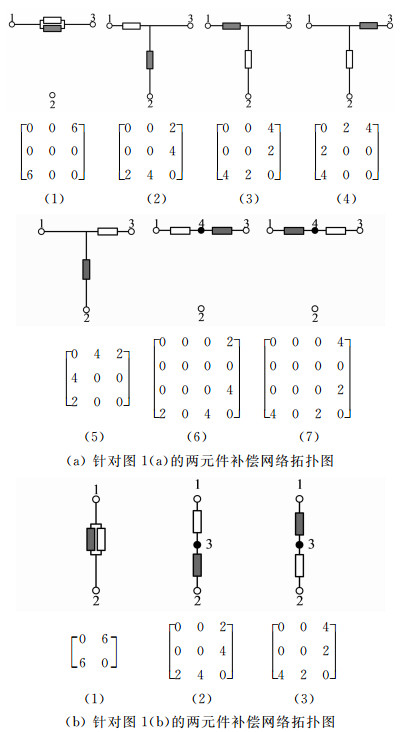
|
| 图 9 两元件补偿网络拓扑图 Fig. 9 Topologies composed of two compensation elements |
假设2个元件都是有源滤波器APF,那么根据图 9就可以得到图 10所示的补偿网络.由于2个元件都是APF,由图 9(a)中的(2)和(3)、(4)和(5)、(6)和(7)、图 9(b)中的(2)和(3)拓扑分别得到的补偿网络是重复的.因此,不重复的补偿网络有6个,这和文献[13]的分析结果一致,验证了本文方法的正确性和有效性.
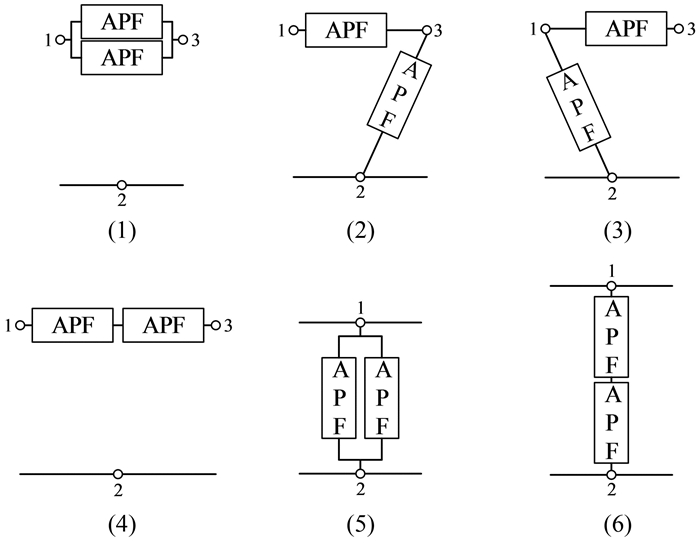
|
| 图 10 2个APF的混合补偿网络 Fig. 10 Compensation network composed of two active power filter (APF) |
假设拓扑中的有源元件为有源滤波器APF,无源元件为基波下低阻的无源滤波器PF1或谐波下低阻的无源滤波器PF2.得到的2元件和3元件混合APF拓扑数目与文献[13]的结果相比较,如表 1所示.
| 拓扑组成 | 本文辨识的拓扑数 | 功能上不重复的拓扑数 | 文献辨识的拓扑数 |
| APF+PF1 | 10 | 9 | 4 |
| APF+PF2 | 10 | 9 | 4 |
| APF+PF1+PF2 | 86 | 30 | 13 |
| APF+PF1+PF1 | 86 | 6 | 2 |
| APF+PF2+PF2 | 86 | 10 | 3 |
如表 1所示,由本文方法辨识出的APF与PF1组成拓扑有10种,排除功能上重复的拓扑则有9种,是文献[13]辨识出的电气连接有效的拓扑的2倍多.对于3元件的混合补偿系统,本文辨识出的拓扑远远多于文献[13],这说明了本文方法在拓扑辨识方面更加全面.
6 结语提出一种混合补偿系统补偿网络的计算机辨识和分析新方法,基于深度优先搜索算法编写出计算机辨识程序.该计算机程序仅需要输入元件数,即可辨识出电气连接有效混合补偿系统的拓扑图,再通过设定元件类型即可得出混合补偿系统的具体拓扑.算例对2元件和3元件混合补偿系统进行分析,与文献[13]结果相比较,验证本文方法的正确性和有效性,在拓扑辨识方面更加全面.
| [1] |
罗世国, 连级三. 一种新型谐波配合补偿系统初探[J]. 铁道学报, 1995, 17(s1): 42-46. Luo Shiguo, Lian Jisan. Tentative exploration on a new combined compensation system to harmonic[J]. Journal of the China Railway Society, 1995, 17(s1): 42-46. |
| [2] |
郑琼林, 路国锋, 郝荣泰. 能降低端电压和容量的有源电力滤波器并联混合补偿拓扑结构研究[J]. 北京交通大学学报, 1999, 23(2): 45-48. Zheng Qionglin, Lu Guofeng, Hao Rongtai. A probe in shunt hybrid-compensator topology with reduced APF's rating and terminal-voltage[J]. Journal of Northern Jiaotong University, 1999, 23(2): 45-48. DOI:10.3969/j.issn.1673-0291.1999.02.011 |
| [3] |
邓占锋, 朱东起, 姜新建. 降低有源部分容量的混合电力滤波器[J]. 清华大学学报(自然科学版), 2003, 43(3): 293-295. Deng Zhanfeng, Zhu Dongqi, Jiang Xinjian. Reduced rating of active filter in hybrid power filter[J]. Journal of Tsinghua University(Science and Technology), 2003, 43(3): 293-295. DOI:10.3321/j.issn:1000-0054.2003.03.004 |
| [4] |
刘飞, 邹云屏, 李辉. C型混合有源电力滤波器[J]. 中国电机工程学报, 2005, 25(6): 75-80. Liu Fei, Zou Yunping, Li Hui. The C type hybrid active power filter[J]. Proceedings of the CSEE, 2005, 25(6): 75-80. DOI:10.3321/j.issn:0258-8013.2005.06.014 |
| [5] |
唐杰, 罗安, 范瑞祥, 等. 无功补偿和混合滤波综合补偿系统及其应用[J]. 中国电机工程学报, 2007, 27(1): 88-92. Tang Jie, Luo An, Fan Ruixiang, et al. Combinedcompensation system with reactive power compensation and hybrid active power filter and its engineering application[J]. Proceedings of the CSEE, 2007, 27(1): 88-92. DOI:10.3321/j.issn:0258-8013.2007.01.016 |
| [6] |
吴卫民, 童立青, 钱照明, 等. 一种高性能串联混合有源电力滤波器拓扑的研究[J]. 中国电机工程学报, 2004, 24(12): 108-112. Wu Weiming, Tong Liqing, Qian Zhaoming, et al. Analysis of a novel hybrid series active power filter topology[J]. Proceedings of the CSEE, 2004, 24(12): 108-112. DOI:10.3321/j.issn:0258-8013.2004.12.021 |
| [7] |
张定华, 桂卫华, 王卫安, 等. 新型电气化铁道电能质量综合补偿系统的研究及工程应用[J]. 电工技术学报, 2009, 24(3): 189-194. Zhang Dinghua, Gui Weihua, Wang Weian, et al. Study and application of a new power quality combined compensation system for electrified railway[J]. Transactions of China Electrotechnical Society, 2009, 24(3): 189-194. DOI:10.3321/j.issn:1000-6753.2009.03.033 |
| [8] |
张志文, 王丹, 胡斯佳, 等. 一种混合型电气化铁道电能质量综合治理系统及其容量分析[J]. 电力自动化设备, 2014, 34(12): 89-94. Zhang Zhiwen, Wang Dan, Hu Sijia, et al. Hybrid railway power quality improvement system and its power capacity analysis[J]. Electric Power Automation Equipment, 2014, 34(12): 89-94. DOI:10.3969/j.issn.1006-6047.2014.12.015 |
| [9] |
孙佐, 王念春. 并联混合有源电力滤波器拓扑比较研究[J]. 电力电子技术, 2008, 42(1): 9-11. Sun Zuo, Wang Nianchun. A study on comparison of parallel hybrid active power filter topologies[J]. Power Electronics, 2008, 42(1): 9-11. DOI:10.3969/j.issn.1000-100X.2008.01.004 |
| [10] |
王果, 田铭兴, 任恩恩. 降低电气化铁路混合有源补偿装置有源支路容量的分析[J]. 电力自动化设备, 2010, 30(9): 18-23. Wang Guo, Tian Mingxing, Ren Enen. Reduced active part rating of hybrid active compensation for electrification railway[J]. Electric Power Automation Equipment, 2010, 30(9): 18-23. DOI:10.3969/j.issn.1006-6047.2010.09.004 |
| [11] |
Demirdelen T, Inci M, Bayindir K C, et al. Review of hybrid active power filter topologies and controlers[C]// Fourth International Conference on Power Engineering, Energy and Electrical Drives. IEEE, 2013: 587-592.
|
| [12] |
Peng F Z. Harmonic sources and filtering approaches[J]. IEEE Industry Applications Magazine, 2001, 7(4): 18-25. DOI:10.1109/2943.930987 |
| [13] |
王果, 田铭兴, 任恩恩, 等. 电气化铁路有源补偿结构的拓扑辨识及分析[J]. 电力自动化设备, 2012, 32(1): 49-53. Wang Guo, Tian Mingxing, Ren Enen, et al. Identification and analysis of active compensation topology for electric railroads[J]. Electric Power Automation Equipment, 2012, 32(1): 49-53. DOI:10.3969/j.issn.1006-6047.2012.01.010 |
| [14] |
兰家隆, 刘军. 应用图论及算法[M]. 成都: 电子科技大学出版社, 1995. Lan Jialong, Liu Jun. Applications Graph Theory and Algorithm[M]. Chengdu: UESTC Press, 1995. |
| [15] |
梅义, 丘东元, 张波. 基于深度优先搜索的潜在电路计算机辅助分析法[J]. 中国电机工程学报, 2008, 28(24): 75-81. Mei Yi, Qiu Dongyuan, Zhang Bo. Computer-aided sneak circuit analysis method based on Depth-first search algorithm[J]. Proceedings of the CSEE, 2008, 28(24): 75-81. DOI:10.3321/j.issn:0258-8013.2008.24.013 |
 2019, Vol. 52
2019, Vol. 52