文章信息
- 来文青, 龚庆武, 高春辉, 刘会斌, 刘卫明, 吴留闯, 刘旭, 王波, 乔卉
- LAI Wenqing, GONG Qingwu, GAO Chunhui, LIU Huibin, LIU Weiming, WU Liuchuang, LIU Xu, WANG Bo, Qiao Hui
- 基于特征量和卷积神经网络的暂态电压稳定评估
- Transient voltage stability evaluation based on feature and convolutional neural network
- 武汉大学学报(工学版), 2019, 52(9): 815-823, 835
- Engineering Journal of Wuhan University, 2019, 52(9): 815-823, 835
- http://dx.doi.org/10.14188/j.1671-8844.2019-09-010
-
文章历史
- 收稿日期: 2018-10-02
2. 武汉大学电气与自动化学院, 湖北 武汉 430072;
3. 国网内蒙古东部电力有限公司电力科学研究院, 内蒙古 呼和浩特 010000
2. School of Electrical Engineering and Automation, Wuhan University, Wuhan 430072, China;
3. Electric Power Research Institute, State Grid Inner Mongolia Eastern Power Company Limited, Hohhot 010000, China
随着跨省互联大规模电网和交直流输电线路投入运行,我国电力系统的安全稳定运行面临着重大的考验.为避免出现类似印度、西欧、美国大停电等特大安全事故[1-3],对电网进行暂态稳定评估研究是很有必要的.
电力系统暂态稳定评估(transient stability assessment, TSA)是促进电力系统稳定安全运行的重要方法[4].暂态电压稳定问题主要有以下3个特点[5-8]:暂态电压失稳机理复杂,在已有文献和研究中还未能提出可用于电力系统暂态电压失稳分析的普适性理论;目前,普遍认为电力系统电压稳定问题并不是静态问题,本质上来说是一个动态稳定问题,与系统元件的动态特性有很大关系,每个元件对电压稳定的影响程度又各不相同,因此难以建立一个既能准确描述电力系统电压稳定性能又能在工程应用中使用的简化模型;电力系统中感应电动机等负荷的动态变化特性引起的暂态电压失稳过程非常迅速,时间跨度为0.1~10 s,若不能及时处理故障,会对系统的稳定造成更大的损害.这3大特点使得电力系统暂态电压稳定问题一直是稳定分析中的重点突出问题.
目前,时域法、直接法是传统的暂态电压稳定评估方法中的主流方法.时域法虽然结果较为准确,但是计算量大、时间长不能满足快速性的要求;而直接法精度不高、计算结果偏保守,只适用于简单系统,能否应用于复杂模型下仍有待研究.这两种传统方法都不能完全满足在线暂态电压稳定评估要求[9].文献[10]提出了依据故障发生前后暂态过程中戴维南等值参数的变化来判断电力系统稳定状态的方法,但在电力系统暂态过程中戴维南参数是不断变化的,而且现有算法的精度和时间无法满足在线暂态电压稳定评估的要求.
因此,在目前暂态电压稳定机理尚不明确的情况下,迫切需要一种电力系统在线暂态电压稳定评估方法,该方法不仅要能够判别出电力系统故障后暂态电压的稳定趋势,还要综合考虑其失稳的变化特点,能够满足暂态电压在线稳定判别评估准确性和快速性的要求.
基于数据驱动的实时暂态电压稳定评估能够不依赖具体的电网物理模型,在评估过程中避开了复杂的失稳机理,通过大量的离线训练更新分类参数来处理非线性问题,时耗短、在线实时应用性强,因此尤其适合于暂态电压稳定的在线评估[11].目前采用人工神经网络(artificial neural networks, ANN)[11]、支持向量机(support vector machines, SVM)[12]、核心向量机(core vector machine, CVM)[13]虽然能实现较高的评估精度, 但其研究对象都是关于功角暂态稳定;文献[14]通过时序特征提取和融入错分代价的决策树算法,降低对失稳案例漏判概率,但其模型分类准确率不高.
卷积神经网络(convolutional neural network, CNN)在语音识别领域能在保证性能的前提下简化网络模型,识别准确率高,泛化能力强[15].在图像处理领域,卷积神经网络能够通过卷积从图像像素中提取图像特征,权值共享和池化使CNN网络需要训练的参数大大减小, 优化了网络结构,提高了训练的效率[16].CNN通过局部连接、权重共享、池化来充分利用数据的局部特征,优化网络结构,特征提取能力强且具有良好的鲁棒特性和泛化能力,与其他种类的分类器模型相比拥有高准确率和低时空复杂度,在计算机深度学习领域已得到应用[17],因此将其引入电力系统的暂态电压稳定判别,能够实现对电力系统暂态电压稳定的在线判别.
本文将卷积神经网络CNN引入电力系统暂态电压稳定评估.将电力系统的暂态电压稳定视为一个二分类问题,提出一种基于特征量和卷积神经网络的电力系统暂态电压稳定评估.首先基于传统电压稳定指标分解及响应数据,从原始电气量中构建电压稳定特征量,进行离线训练,将故障后系统的一些在线实时数据构建特征量后输入到已经离线训练生成的CNN模型中,可以准确快速判断出电力系统暂态电压稳定状态信息.仿真结果表明,该方法错误率低至0.5%、精确率高达99.48%、测试时间低至0.051 s,能够准确快速判断出电力系统暂态电压稳定状态,可以作为辅助判稳措施.
1 基于传统指标分解及响应数据的电压稳定特征量构建基于特征量和卷积神经网络CNN的电力系统电压暂态稳定评估中的关键一步是选取合适的特征量作为输入,通过选取科学合理的特征量可以提高评估的准确性和快速性.
暂态电压失稳机理复杂,在已有文献和研究中还未能提出可用于电力系统暂态电压失稳分析的普适性理论.本文通过普遍接受的经典电压指标分解和响应数据构建特征量,分析文献[18-25]中的经典电压指标:暂态灵敏度、局部负荷裕度、暂态潮流奇异值和特征值、能量函数、二阶指标、邻近电压崩溃、试验函数等,可以发现在电压稳定的分析过程中,通常会涉及到下述电气响应量:支路的有功Qi、无功Pi和电流Ii,节点有功Pb和无功Qb,发电机的无功Qg,节点的电压幅值Vm和相角φ.
在实际电网中,支路、节点数目异常庞大,直接使用上述电气量作为卷积神经网络的输入会使得输入维数过大,造成维数灾难,影响效率.因此,本文选择上述8个电气量的统计分析量作为输入,同时综合考虑暂态电压稳定的动态发展过程,选择系统故障发生之前、故障发生的瞬间以及故障切除的瞬间多个时刻来构建CNN的输入特征量.
1) 特征量1:故障前发电机无功之和为
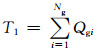 (1)
(1)
式中:Ng为电网中发电机数; Qgi表示故障前第i台发电机发出的无功功率,该特征量反映了故障发生前电力系统中发电机无功出力情况.
2) 特征量2、3:故障前节点的有功和无功之和为
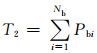 (2)
(2)
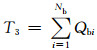 (3)
(3)
式中:Nb为电网节点数;Pbi、Qbi分别为故障前第i个节点有功功率和无功功率.这2个特征量反映了故障发生前节点上的功率情况,当系统处于电压稳定时,节点处的有功与附近节点的负荷需求之间达到平衡,一旦故障后这种平衡被打破,可能导致暂态电压失稳.
3) 特征量4、5:故障前各支路有功和无功之和为
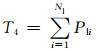 (4)
(4)
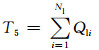 (5)
(5)
式中:Nl为电网支路数;Pli、Qli分别表示故障前第i条支路有功功率和无功功率.该系列特征量表征了系统内部对电压的支撑能力.
4) 特征量6~8:故障前节点电压最大值、最小值和均值为
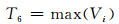 (6)
(6)
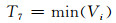 (7)
(7)
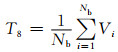 (8)
(8)
式中:Vi表示故障前第i个节点电压.该系列特征量表征了故障前系统的电压运行压力的程度.
5) 特征量9~11:故障前支路电流的最大值、最小值、方差为
 (9)
(9)
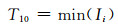 (10)
(10)
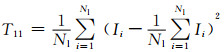 (11)
(11)
式中:Ii表示故障前第i条支路电流.该系列特征量表征了故障前系统的电流运行压力的程度.
6) 特征量12~14:t0故障发生时刻支路电流变化率的最大值、最小值、方差为
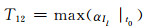 (12)
(12)
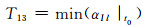 (13)
(13)
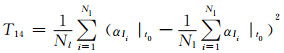 (14)
(14)
式中:αIi|t0为故障发生时刻第i条支路电流变化率.
7) 特征量15~17:t0故障发生时刻节点电压变化率的最大值、最小值、方差为
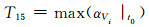 (15)
(15)
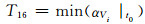 (16)
(16)
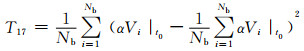 (17)
(17)
式中:αVi|t0为故障发生时刻节点电压变化率.
8) 特征量18~20:t1故障切除时刻发电机无功加速的最大值、均值和方差为
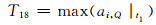 (18)
(18)
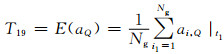 (19)
(19)
 (20)
(20)
式中:ai, Q|t1为故障切除时刻第i台发电机无功加速度.
9) 特征量21~23:t1故障切除时刻支路电流最大值、最小值、方差为
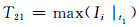 (21)
(21)
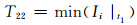 (22)
(22)
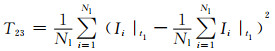 (23)
(23)
式中:Ii|t1为故障切除时刻第i条支路电流.
10) 特征量24~26:t1故障切除时刻节点电压变化率的最大值、最小值、方差为
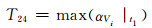 (24)
(24)
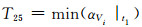 (25)
(25)
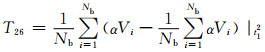 (26)
(26)
式中:αVi|t1为故障切除时刻第i个节点电压变化率.
11) 特征量27~29:从t0到t1时刻系统各发电机无功变化的最大值、均值及方差为
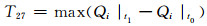 (27)
(27)
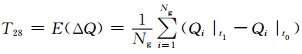 (28)
(28)
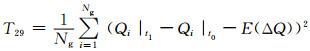 (29)
(29)
式中:Qi|t1、Qi|t0分别为第i台发电机故障切除时刻和故障发生时刻的无功功率.
12) 特征量30~31:从t0到t1时刻各节点电压相角变化量的最大值、均值与方差为
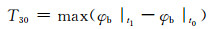 (30)
(30)
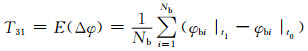 (31)
(31)
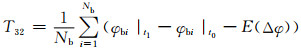 (32)
(32)
式中:φbi|t1、φbi|t0分别为第i个节点故障切除时刻和故障发生时刻的相角.
13) 特征量33~34:从t0到t1时刻支路有功和无功变化量之和为
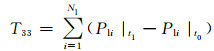 (33)
(33)
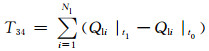 (34)
(34)
式中:Pli|t1、Pli|t0分别为第i条支路故障切除时刻和故障发生时刻的有功功率;Qli|t1、Qli|t0分别为第i台发电机故障切除时刻和故障发生时刻的无功功率.
14) 特征量35~36:从t0到t1时刻节点有功和无功之和变化量为
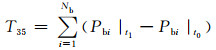 (35)
(35)
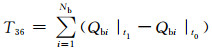 (36)
(36)
式中:Pbi|t1、Pbi|t0分别为第i条支路故障切除时刻和故障发生时刻的有功功率;Qbi|t1、Qbi|t0分别为第i台发电机故障切除时刻和故障发生时刻的无功功率.
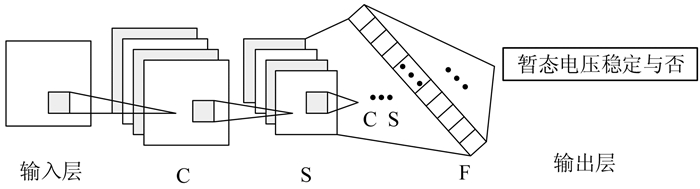
2 卷积神经网络卷积神经网络是一种特殊的深度学习人工神经网络,由输入层、卷积层(convolution layer,C)、采样层(subsamping layer,S)、全连接层(fully connected layer,F)和输出层组成.卷积层和采样层交替出现,上一层的输出作为下一层的输入,而在最后是一维的全连接网络[26],其结构如图 1所示.
|
| 图 1 卷积神经网络CNN结构 Fig. 1 Convolutional neural network CNN structure |
卷积层可以由多个特征图组成,输入通过卷积核与前一层连接,每个神经元与上一层多个特征图局部相连,每个神经元对应的卷积核不一样,保证特征提取充分[27].其输出为
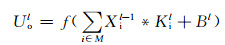 (37)
(37)
式中:Uol为卷积层l的输出;Xil-1为卷积层l层输入;Kil为对应的卷积核;M为卷积层l层的输入子集;f(·)为激活函数;Bl是加偏置;“*”为卷积符号.
2.2 采样层采样层S层(subsamping layer)每个特征矩阵都与卷积层C层一一对应,利用局部相关性,对卷积层的特征图进行特征采样、降维,能够在减少数据处理量的同时又保留有用信息[16],输出为
 (38)
(38)
式中:Uol为采样层l的输出特征图;f(·)为激活函数;βl为采样层S的权重系数;fdown(·)为采样函数;Xil-1为采样层l的输入特征图;Bl为采样层的偏置.
2.3 全连接层CNN中全连接层F层(fully connected layer)的神经元与上一层的神经元全部连接,将二维的特征图拼接为一维特征作为全连接网络的输入,其输出为
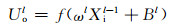 (39)
(39)
式中:Uol为全连接层输出;ωl为F层权重系数;Bl为F层偏置.
2.4 输出层输出层由径向基函数(euclidean radial basis function,ERBF)单元组成,输入离参数向量越远,ERBF输出越大,可以被理解为衡量输入模式和与ERBF相关联类的一个模型匹配程度的惩罚项[28].
CNN中损失函数用来衡量对结果的不满意程度,可用交叉熵函数表示为
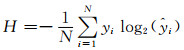 (40)
(40)
式中:yi为训练集对应的第i个标签实际值; 
CNN反向传播是基于梯度下降法,使初置的网络参数向误差小的方向调整,以此来不断提高分类的正确率.
3 基于特征量和卷积神经网络的暂态电压稳定评估流程基于特征量和卷积神经网络CNN的电力系统暂态电压稳定评估的总体流程如图 2所示,包括:构建输入特征集合、在线构建特征量、基于CNN的暂态电压稳定评估和评价指标计算等4个部分,通过离线仿真得到的海量数据样本训练一个完整的暂态电压稳定评估模型,在以后的每一个数据采集节点,利用该模型即可对系统实时获取的量测数据完成一次暂态电压稳定评估过程.
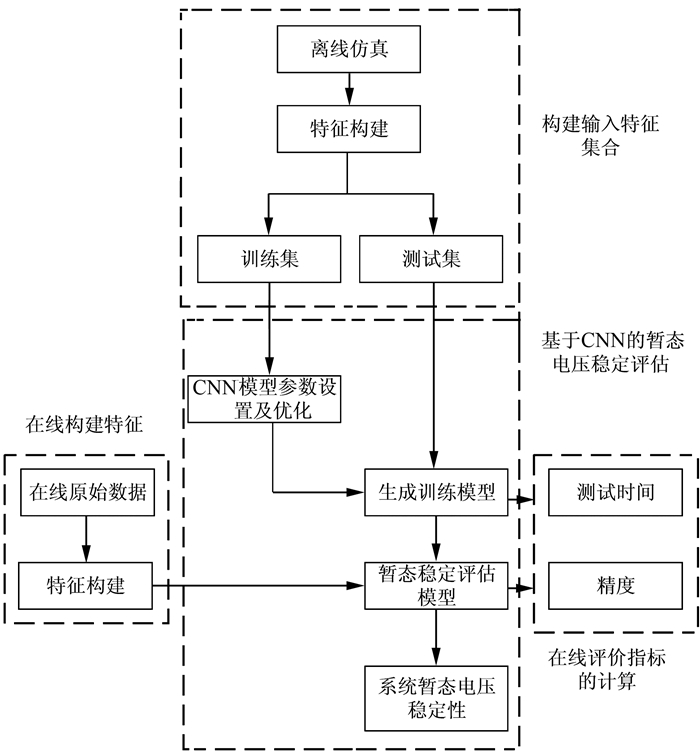
|
| 图 2 基于特征量和CNN的电力系统暂态电压稳定评估流程 Fig. 2 Power system transient voltage stability evaluation process based on feature and CNN |
暂态电压稳定评估的重要一步是构建科学合理的特征量.本文进行了基于传统指标分解及响应数据的电压稳定特征量构建,形成36维的特征,能够表示系统暂态电压稳定的特性,可以反映电力系统的网架结构、运行状态、暂态电压稳定的发展过程.
可以通过离线的仿真来生成原始输入特征,仿真时应该设置尽量多的潮流运行方式和故障方式来构建原始输入特征作为训练集和测试集.此外,历史运行数据也可以用来生成或者作为特征量.
3.2 在线构建特征量在线特征构建是基于在线PMU量测数据,本文基于传统指标分解及响应数据构建电压稳定特征量,形成36维的特征量,表示系统运行状态和暂态电压发展过程.
3.3 基于特征量和CNN的暂态电压稳定评估这一阶段的任务有2个,一是离线训练生成暂态稳定评估模型;二是通过将构建的在线特征量输入暂态稳定评估模型中来实现特征提取和稳定关系挖掘分类,完成暂态电压稳定评估.
3.4 评价指标计算基于特征量和卷积神经网络的电力系统暂态电压稳定评估的评价性能选取错误率、精确率以及测试时间等指标.
电力系统暂态电压稳定评估是一个二分类问题,根据分类器测试数据集上的预测正确或不正确,可以分为4种情况,如表 1所示.
表 1中,n11表示将实际是稳定状态识别预测为稳定状态样本数,n10表示将实际是稳定状态识别预测为不稳定状态样本数,n01表示将实际是不稳定状态识别预测为稳定状态样本数,n00表示将实际是不稳定状态识别预测为不稳定状态样本数.
预测的错误率er(error rate)为预测错误的样本数除以总的样本数:
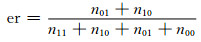 (41)
(41)
在电力系统中,n01与n10对电网造成的危害是不一样的.前者往往更易造成系统的不可逆恶化和崩溃,而后者则往往可以通过后续控制来挽回损失,产生的后果影响相对较小.因此,为了衡量不同分类器模型对稳定样本的预测能力,引入精确率pr(precision)(在预测结果中,预测为稳定的样本中,正确预测为稳定样本的概率)来作为衡量预测性能的一个指标, 该指标越大则预测效果越好:
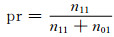 (42)
(42)
均方差(mean square error,MSE)为目标变量与预测值之间距离平方之和的平均值:
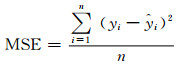 (43)
(43)
式中:yi为实际值; 
本文的仿真模型为新英格兰10机39节点典型电力系统.仿真计算在PSD-BPA和Matlab中进行,仿真在配置为Intel(R) Core(TM)i7-8700、3.2GHz CPU、16GB RAM的计算机上进行.
新英格兰10机39节点系统是美国新英格兰镇的一个真实电力网络.该标准算例拥有10台发电机、39条母线以及46条交流线,基准功率为100 MVA,基准电压为345 kV.负荷模型设为9种(80%、85%、90%、95%、100%、105%、110%、115%、120%),同时按照相应的比例改变发电机的出力状态.在9中运行方式下进行潮流计算,如果潮流收敛,则进行暂态计算.三相短路或单相短路故障位置设置在线路首段的0%、10%、20%、30%、40%、50%、60%、70%、80%、90%处.仿真时间设置为:故障发生时刻为10周波(0.2 s);故障切除时刻为20周波(0.4 s).
暂态电压稳定判据为母线电压持续低于0.75 pu的时间不超过1 s[29].故分类1(稳定):母线电压持续低于0.75 pu的时间不超过1 s;分类0(不稳定):母线电压持续低于0.75 pu的时间超过1 s.
从仿真结果中选择6 000个样本,其中4 000个样本作为训练集,训练集中有1 939个暂态电压稳定样本和2 061个暂态电压失稳样本;另外的2 000个作为测试集,测试集中有969个暂态电压稳定样本和1 031个暂态电压失稳样本.将训练集输入CNN模型进行训练,测试集作为模型验证.
4.1 CNN训练网络参数本文采用的CNN网络结构为4层,包含了2个C层和2个S层[30].为寻找合适的CNN训练网络,预设批处理数为50,训练次数为10,设置不同的网络结构与卷积核大小进行训练测试.
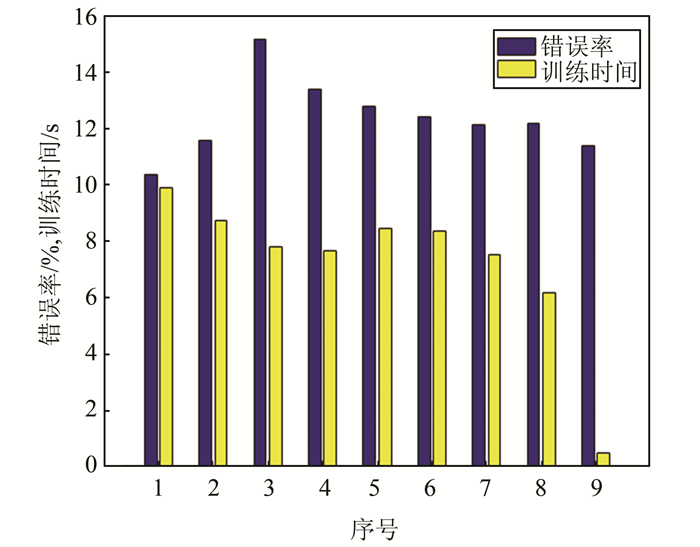
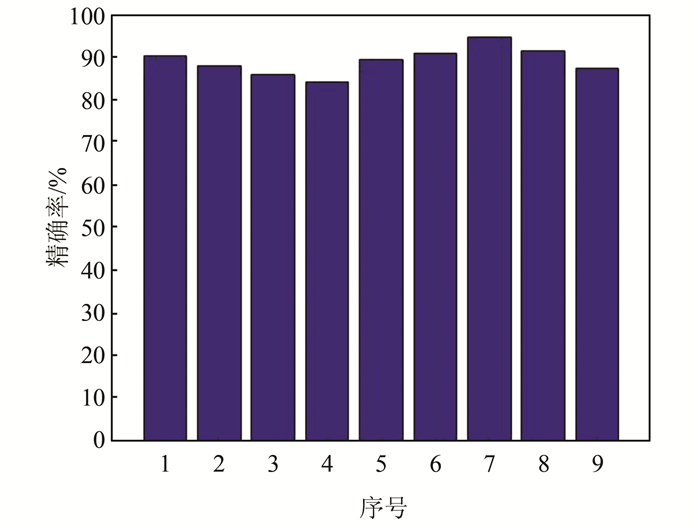
训练测试结果如表 2、图 3和4所示,序号1对应的网架结构为6C-1S-16C-1S, 2个卷积核大小为1×1和2×2的CNN错误率较低,精确率较高,训练时间虽然较长,但由于是离线训练,并不影响在线计算,故选择此结构的CNN进行训练.
| 序号 | CNN网络结构 | 卷积核 | 错误率/% | 精确率/% | 训练时间/s |
| 1 | 6C-1S-16C-1S | 1 2 | 10.40 | 90.18 | 9.891 0 |
| 2 | 6C-1S-16C-1S | 2 2 | 11.60 | 87.79 | 8.743 0 |
| 3 | 6C-1S-16C-1S | 3 2 | 15.20 | 85.95 | 7.835 0 |
| 4 | 6C-1S-16C-1S | 3 3 | 13.40 | 84.20 | 7.656 0 |
| 5 | 6C-1S-16C-2S | 2 2 | 12.80 | 89.48 | 8.479 0 |
| 6 | 6C-1S-16C-2S | 2 4 | 12.45 | 90.72 | 8.354 0 |
| 7 | 6C-1S-16C-2S | 3 3 | 12.15 | 94.49 | 7.547 0 |
| 8 | 6C-1S-16C-3S | 4 2 | 12.20 | 91.33 | 6.912 0 |
| 9 | 1C-1S-1C-1S | 1 1 | 11.40 | 87.24 | 0.471 0 |
|
| 图 3 不同CNN结构下数据错误率和训练时间 Fig. 3 Data error rate and training time under different CNN structures |
|
| 图 4 不同CNN结构下数据精确率 Fig. 4 Data accuracy rate under different CNN structures |
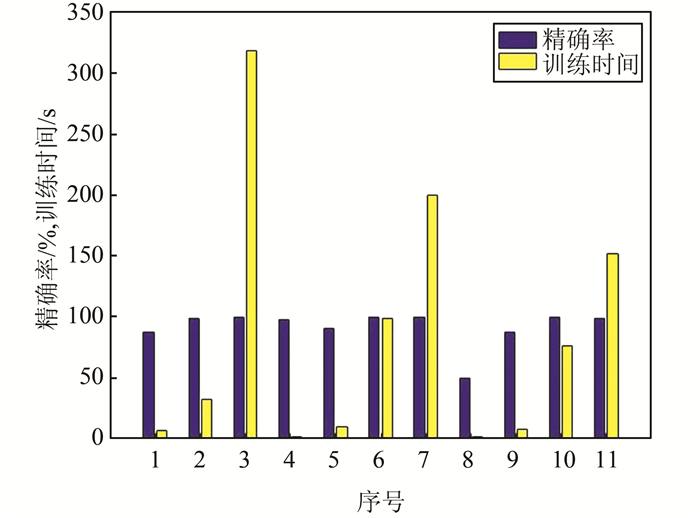
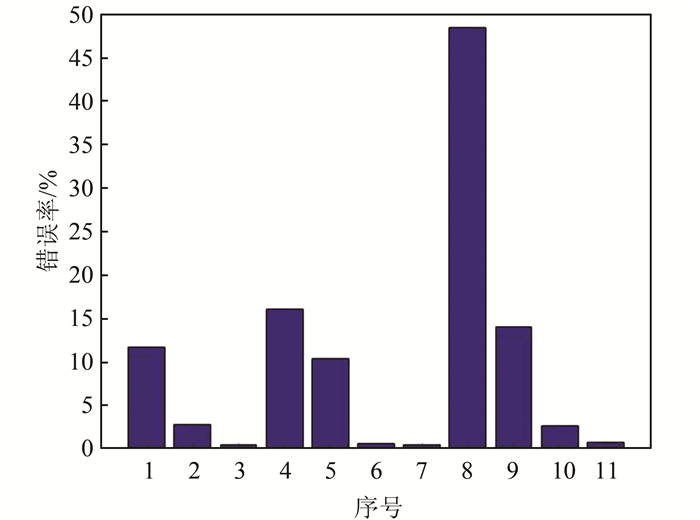
在表 2序号1对应的CNN网络结构下,设置不同的批处理数(每一批处理的样本数)和训练次数,得到对应的错误率、精确率以及训练时间,结果如表 3、图 5和6所示.从中可以发现:当批处理次数保持不变时,训练次数越多,权值调整次数就越高,错误率就会越低,精确率就越高,训练时间就越长;当训练次数一定时,批处理数越小,权值调整次数就越高,错误率就越低,精确率就越高,训练时间也越长.从表 3中可知,序号3的错误率最低,仅为0.5%,精确率达到了99.48%,训练时间虽然较长,但由于是离线训练,并不影响在线测试,此时的CNN结构较好.
| 序号 | 批处理数 | 训练次数 | 错误率/% | 精确率/% | 训练时间/s |
| 1 | 10 | 2 | 11.700 | 87.54 | 6.354 0 |
| 2 | 10 | 10 | 2.850 | 98.82 | 31.710 0 |
| 3 | 10 | 100 | 0.500 | 99.48 | 318.080 0 |
| 4 | 50 | 2 | 16.150 | 97.50 | 2.010 0 |
| 5 | 50 | 10 | 10.400 | 90.18 | 9.957 0 |
| 6 | 50 | 100 | 0.650 | 99.48 | 98.949 0 |
| 7 | 50 | 200 | 0.550 | 99.28 | 199.509 0 |
| 7 | 100 | 2 | 48.450 | 49.45 | 1.535 0 |
| 8 | 100 | 10 | 14.000 | 86.84 | 7.582 0 |
| 9 | 100 | 100 | 2.700 | 99.04 | 76.317 0 |
| 11 | 100 | 200 | 0.800 | 98.77 | 151.921 0 |
|
| 图 5 不同批处理数和训练次数数据精确率和训练时间 Fig. 5 Data accayacies and training times for different batches and training times |
|
| 图 6 不同批处理数和训练次数数据错误率 Fig. 6 Data error rate for different batches and training times |
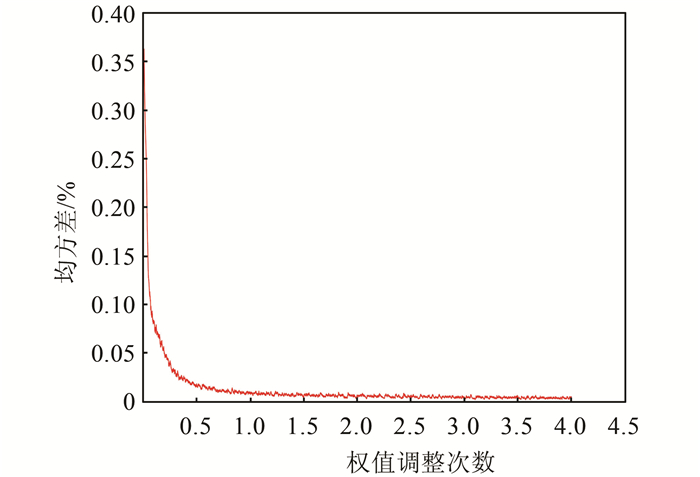
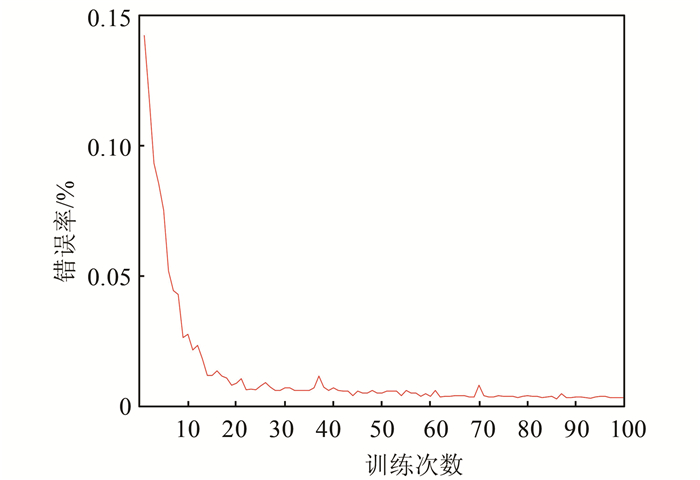
对表 3中序号3的测试结果进行分析,其均方差与权值调整次数的关系如图 7所示,随着权值调整次数的增加,均方差逐渐减小,最后趋于0.5%左右;错误率与训练次数的关系如图 8所示,随着训练次数的增加,测试的错误率逐渐降低,最后趋于0.5%左右.
|
| 图 7 权值调整次数与均方差关系 Fig. 7 Relationship between weight adjustment times and mean square error |
|
| 图 8 训练次数与错误率关系 Fig. 8 Relationship between training times and error rate |
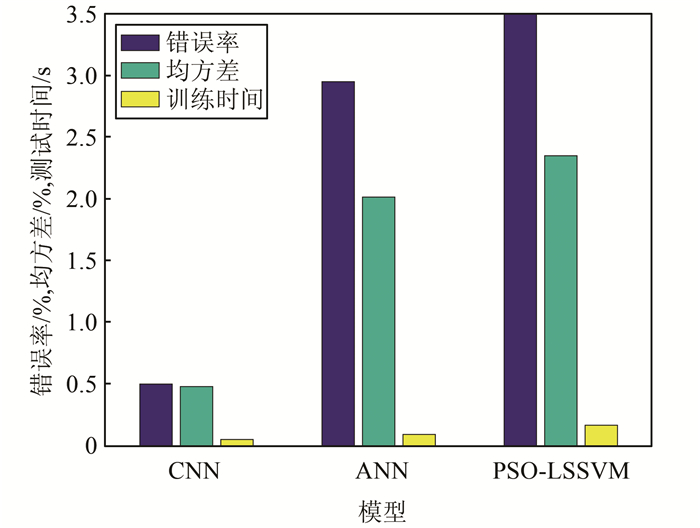
在上节中CNN网架结构为6C-1S-16C-1S, 2个卷积核大小为1×1和2×2、批处理数位为10、训练次数为100的CNN下对4 000组训练样本进行训练、对2 000组测试样本进行测试,以检验暂态电压稳定评估的性能,指标为误差率、精确率、均方差和测试时间,并与神经网络(artificial neural networks, ANN)和粒子群优化的最小二乘支持向量机(particle swarm optimization least squares support vector machine, PSO-LSSVM)的仿真结果进行对比分析.结果如表 4、图 9、图 10所示.
| 模型 | 错误率/% | 精确率pr/% | 均方差MSE/% | 测试时间/s |
| CNN | 0.50 | 99.48 | 0.480 | 0.051 |
| ANN | 2.95 | 99.46 | 2.015 | 0.092 |
| PSO-LSSVM | 3.50 | 97.43 | 2.350 | 0.167 |
|
| 图 9 不同模型的错误率、均方差和测试时间 Fig. 9 Error rate, mean square error and test time for different models |
|
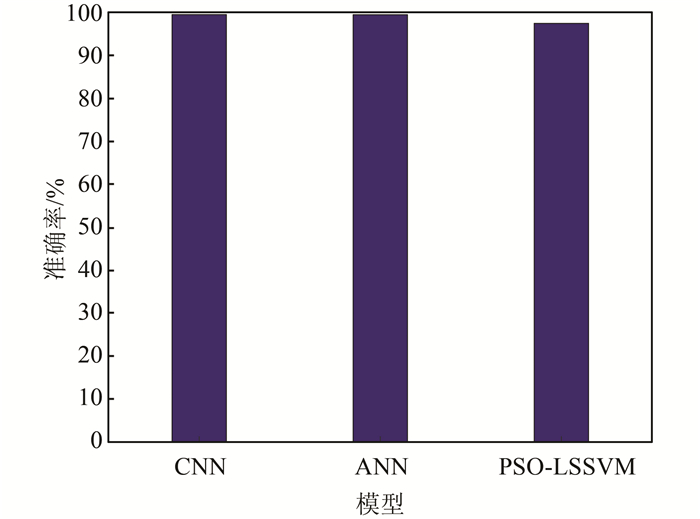
| 图 10 不同模型精确率 Fig. 10 Precisions of different models |
1) 相比于其他2种模型,基于特征量和CNN的暂态电压稳定评估仅有0.5%的错误率,是所有分类器中最低的,同时均方差也最低,仅有0.480%,精确率最高,达99.48%,从中可以看出,基于特征量和卷积神经网络CNN的暂态电压稳定评估效果明显好于其他模型.
2) 从特征量输入到稳定结果输出的时间仅为0.051 s,这是传统方法目前无法做到的,意味着基于特征量和卷积神经网络CNN的暂态电压稳定评估在故障切除后0.1 s以内,即可判断出电力系统是否能够保持暂态电压稳定运行状态,为电力系统后续的控制提供了快速、可靠的信息,可以作为辅助判稳手段,与其他类型的判稳方法相互补充.
5 结论本文首次将卷积神经网络CNN引入电力系统的暂态电压稳定评估,提出一种基于特征量和卷积神经网络的电力系统暂态电压稳定评估方法.基于传统电压稳定指标分解及响应数据,从原始电气量中构建36维电压稳定特征量;构建了电力系统暂态电压稳定评估模型,并在基于美国新英格兰镇的一个真实电力网络所创建的新英格兰10机39节点标准电网中进行了仿真研究,得到下列结论:
1) 相比于ANN、PSO-LSSVM模型,基于特征量和CNN的暂态电压稳定评估错误率更低、精确性更高,均方差更小、测试时间更短,能同时满足电力系统在线暂态电压稳定评估准确性和快速性的要求.
2) 基于特征量和卷积神经网络CNN的暂态电压稳定评估,从特征量输入到电压稳定结果输出的时间仅为0.051 s,该方法能在切除故障后的0.1 s内判断出电力系统暂态电压的稳定状态,可以作为辅助判稳措施.
本文提出的基于特征量和卷积神经网络CNN的暂态电压稳定评估具有错误率低、精确率高、测试时间短的特点,能满足在线稳定判稳要求.但如果训练数据集与测试数据集的分布不一样,则卷积神经网络CNN识别能力有待进一步检验.
| [1] |
梁志峰, 葛睿, 董昱, 等. 印度"7.30"、"7.31"大停电事故分析及对我国电网调度运行工作的启示[J]. 电网技术, 2013, 37(7): 1841-1848. Liang Zhifeng, Ge Rui, Dong Yu, et al. Analysis of the "7.30" and "7.31" blackouts in India and their implications for power system technology, China's power grid dispatching operation[J]. Power System Technology, 2013, 37(7): 1841-1848. |
| [2] |
方勇杰. 美国"9·8"大停电对连锁故障防控技术的启示[J]. 电力系统自动化, 2012, 36(15): 1-7. Fang Yongjie. Enlightenment of the "9·8" blackout in the United States on the prevention and control technology of cascading failures[J]. Automation of Electric Power Systems, 2012, 36(15): 1-7. |
| [3] |
李再华, 白晓民, 丁剑, 等. 西欧大停电事故分析[J]. 电力系统自动化, 2007, 31(1): 1-3, 32. Li Zaihua, Bai Xiaomin, Ding Jian, et al. Analysis of blackouts in Western Europe[J]. Automation of Electric Power Systems, 2007, 31(1): 1-3, 32. DOI:10.3321/j.issn:1000-1026.2007.01.001 |
| [4] |
李杨.基于广域动态信息的电力系统暂态稳定评估研究[D].北京: 华北电力大学, 2014. Li Yang. Research on transient stability assessment of power system based on wide-area dynamic information[D]. Beijing: North China Electric Power University, 2014. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2658915 |
| [5] |
汤涌, 仲悟之, 孙华东, 等. 电力系统电压稳定机理研究[J]. 电网技术, 2010, 34(4): 24-29. Tang Yong, Zhong Wuzhi, Sun Huadong, et al. Study on voltage stability mechanism of power system[J]. Power System Technology, 2010, 34(4): 24-29. DOI:10.3969/j.issn.1674-0629.2010.04.005 |
| [6] |
仲悟之.受端系统暂态电压稳定机理研究[D].北京: 中国电力科学研究院, 2010. Zhong Wuzhi. Research on transient voltage stability mechanism of receiving system[D].Beijing: China Electric Power Research Institute, 2010. http://cdmd.cnki.com.cn/Article/CDMD-82302-1011043355.htm |
| [7] |
李岩.受端电网暂态电压稳定性研究[D].天津: 天津大学, 2015. Li Yan. Study on transient voltage stability of receiving power grid[D]. Tianjin: Tianjin University, 2015. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D654598 |
| [8] |
孙华东, 周孝信, 李若梅. 感应电动机负荷参数对电力系统暂态电压稳定性的影响[J]. 电网技术, 2005, 29(23): 1-6. Sun Huadong, Zhou Xiaoxin, Li Ruomei. Influence of induction motor load parameters on transient voltage stability of power system[J]. Power System Technology, 2005, 29(23): 1-6. DOI:10.3321/j.issn:1000-3673.2005.23.001 |
| [9] |
刘雷涛.基于机器学习的电力系统暂态稳定评估[D].北京: 华北电力大学, 2017. Liu Leitao. Power system transient stability assessment based on machine learning[D]. Beijing: North China Electric Power University, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10079-1017215199.htm |
| [10] |
汤涌, 孙华东, 易俊, 等. 基于全微分的戴维南等值参数跟踪算法[J]. 中国电机工程学报, 2009, 29(13): 48-53. Tang Yong, Sun Huadong, Yi Jun, et al. The Thevenin-like equivalent parameter tracking algorithm based on total differential[J]. Proceedings of the CSEE, 2009, 29(13): 48-53. DOI:10.3321/j.issn:0258-8013.2009.13.008 |
| [11] |
姚德全.基于神经网络的电力系统暂态稳定评估[D].天津: 天津大学, 2014. Yao Dequan. Power system transient stability assessment based on neural network[D]. Tianjin: Tianjin University, 2014. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D485773 |
| [12] |
叶圣永, 王晓茹, 刘志刚, 等. 基于受扰严重机组特征及机器学习方法的电力系统暂态稳定评估[J]. 中国电机工程学报, 2011, 31(1): 46-51. Ye Shengyong, Wang Xiaoru, Liu Zhigang, et al. Power system transient stability assessment based on disturbed serious unit characteristics and machine learning method[J]. Proceedings of the CSEE, 2011, 31(1): 46-51. |
| [13] |
王亚俊, 王波, 唐飞, 等. 基于响应轨迹和核心向量机的电力系统在线暂态稳定评估[J]. 中国电机工程学报, 2014, 34(19): 3178-3186. Wang Yajun, Wang Bo, Tang Fei, et al. On-line transient stability assessment of power system based on response trajectory and kernel vector machine[J]. Proceedings of the CSEE, 2014, 34(19): 3178-3186. |
| [14] |
朱利鹏, 陆超, 黄河, 等. 基于广域时序深度学习策略的暂态电压稳定评估[J]. 电网技术, 2016, 40(1): 180-185. Zhu Lipeng, Lu Chao, Huang He, et al. Transient voltage stability assessment based on wide-area time series deep learning strategy[J]. Power System Technology, 2016, 40(1): 180-185. |
| [15] |
张晴晴, 刘勇, 潘接林, 等. 基于卷积神经网络的连续语音识别[J]. 北京科技大学学报, 2015, 37(9): 1212-1217. Zhang Qingqing, Liu Yong, Pan Jielin, et al. Continuous speech recognition based on convolutional neural network[J]. Journal of University of Science and Technology Beijing, 2015, 37(9): 1212-1217. |
| [16] |
吴正文.卷积神经网络在图像分类中的应用研究[D].成都: 电子科技大学, 2015. Wu Zhengwen. Application of convolutional neural networks in image classification[D].Chengdu: University of Electronic Science and Technology of China, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10614-1016059916.htm |
| [17] |
李彦冬, 郝宗波, 雷航. 卷积神经网络研究综述[J]. 计算机应用, 2016, 36(9): 2508-2515. Li Yandong, Hao Zongbo, Lei Hang. Review of convolutional neural networks[J]. Journal of Computer Applications, 2016, 36(9): 2508-2515. |
| [18] |
李国庆, 姜涛, 徐秋蒙, 等. 基于局部电压稳定指标的裕度灵敏度分析及应用[J]. 电力自动化设备, 2012, 32(4): 1-5. Li Guoqing, Jiang Tao, Xu Qiumeng, et al. Margin sensitivity analysis and application based on local voltage stability index[J]. Electric Power Automation Equipment, 2012, 32(4): 1-5. DOI:10.3969/j.issn.1006-6047.2012.04.001 |
| [19] |
段献忠, 张德泉. 电力系统电压稳定灵敏度分析方法[J]. 电力系统自动化, 1997, 21(4): 9-12. Duan Xianzhong, Zhang Dequan. Analysis method of voltage stability sensitivity in power system[J]. Automation of Electric Power Systems, 1997, 21(4): 9-12. DOI:10.3321/j.issn:1000-1026.1997.04.004 |
| [20] |
李吉德, 王兴飞. 静态电压稳定性指标研究分析[J]. 国网技术学院学报, 2012, 15(6): 9-11. Li Jide, Wang Xingfei. Research and analysis of static voltage stability index[J]. Journal of State Grid Institute of Technology, 2012, 15(6): 9-11. DOI:10.3969/j.issn.1008-3162.2012.06.003 |
| [21] |
徐志友, 纪延超, 钮文艳, 等. 衡量潮流雅可比矩阵及其降阶阵不对称性和奇异性的指标[J]. 中国电机工程学报, 2006, 26(5): 51-57. Xu Zhiyou, Ji Yanchao, Niu Wenyan, et al. Indicators for measuring the asymmetry and singularity of the trend Jacobian matrix and its reduced order matrix[J]. Proceedings of the CSEE, 2006, 26(5): 51-57. DOI:10.3321/j.issn:0258-8013.2006.05.009 |
| [22] |
郑武, 李华强, 刘慧, 等. 基于静态能量函数法的电压弱节点分析[J]. 电力系统保护与控制, 2010, 38(14): 79-83. Zheng Wu, Li Huaqiang, Liu Hui, et al. Analysis of voltage weak nodes based on static energy function method[J]. Power System Protection and Control, 2010, 38(14): 79-83. |
| [23] |
姜勇, 周双喜, 朱凌志. 电力系统电压静稳分析中的二阶指标[J]. 清华大学学报(自然科学版), 2002, 42(9): 1165-1167. Jiang Yong, Zhou Shuangxi, Zhu Lingzhi. Second-order indicators in voltage static stability analysis of power systems[J]. Journal of Tsinghua University(Science and Technology), 2002, 42(9): 1165-1167. DOI:10.3321/j.issn:1000-0054.2002.09.009 |
| [24] |
张建设, 张尧, 武志刚, 等. 广东电网区域负荷裕度分析[J]. 电网技术, 2006, 30(6): 30-34. Zhang Jianshe, Zhang Yao, Wu Zhigang, et al. Analysis of regional load margin of Guangdong power grid[J]. Power System Technology, 2006, 30(6): 30-34. DOI:10.3321/j.issn:1000-3673.2006.06.006 |
| [25] |
姜彤, 艾琳, 杨以涵. 基于负荷裕度的在线电压稳定指标[J]. 电力自动化设备, 2009, 29(10): 39-42. Jiang Tong, Ai Lin, Yang Yihan. Online voltage stability index based on load margin[J]. Electric Power Automation Equipment, 2009, 29(10): 39-42. DOI:10.3969/j.issn.1006-6047.2009.10.008 |
| [26] |
Sukittanon S, Surendran A C, Platt J C, et al. Convolutional networks for speech detection[C]// INTER SPEECH 2004-ICSLP, 8th International Conference on Spoken Language Processing, Jeju Island, Korea, 2008.
|
| [27] |
Shin H C, Roth Holger R, Gao Mingchen, et al. Deep convolutional neural networks for computer-aided detection: CNN architectures, dataset characteristics and transfer learning[J]. IEEE Transactions on Medical Imaging, 2016, 35(5): 1285-1298. DOI:10.1109/TMI.2016.2528162 |
| [28] |
曲景影, 孙显, 高鑫. 基于CNN模型的高分辨率遥感图像目标识别[J]. 国外电子测量技术, 2016(8): 45-50. Qu Jingying, Sun Xian, Gao Xin. High-resolution remote sensing image target recognition based on CNN model[J]. Foreign Electronic Measurement Technology, 2016(8): 45-50. DOI:10.3969/j.issn.1002-8978.2016.08.011 |
| [29] |
中国南方电网公司.Q/CSG 11004-2009南方电网安全稳定计算分析导则[S], 2009. China Southern Power Grid Corporation. Q/CSG 11004-2009 Southern Power Grid Safety and Stability Calculation Analysis Guide[S], 2009. |
| [30] |
魏东, 龚庆武, 来文青, 等. 基于卷积神经网络的输电线路区内外故障判断及故障选相方法研究[J]. 中国电机工程学报, 2016, 36(S1): 21-28. Wei Dong, Gong Qingwu, Lai Wenqing, et al. Research on fault diagnosis and fault phase selection method in transmission line based on convolutional neural network[J]. Proceedings of the CSEE, 2016, 36(S1): 21-28. |
 2019, Vol. 52
2019, Vol. 52




