武汉大学学报(工学版)   2016, Vol. 49 Issue (2): 229-235

文章信息

徐腊梅, 彭俭, 许云峰, 潘轩宇, 陶敏, 朱贝尔
XU Lamei, PENG Jian, XU Yunfeng, PAN Xuanyu, TAO Min, ZHU Beier
基于90kW 无刷双馈发电系统的能量回馈系统
Research on energy feedback system based on 90 kW brushless doubly-fed generation system
武汉大学学报(工学版), 2016, 49(2): 229-235
Engineering Journal of Wuhan University, 2016, 49(2): 229-235
http://dx.doi.org/10.14188/j.1671-8844.2016-02-012

文章历史

收稿日期: 2014-12-16
 Abstract              PDF               Figures               Tables
引用本文 0
徐腊梅, 彭俭, 许云峰, 潘轩宇, 陶敏, 朱贝尔. 基于90kW 无刷双馈发电系统的能量回馈系统[J]. 武汉大学学报(工学版), 2016, 49(2): 229-235.
XU Lamei, PENG Jian, XU Yunfeng, PAN Xuanyu, TAO Min, ZHU Beier. Research on energy feedback system based on 90 kW brushless doubly-fed generation system[J]. Engineering Journal of Wuhan University, 2016, 49(2): 229-235.
基于90kW 无刷双馈发电系统的能量回馈系统
徐腊梅1, 彭俭1, 许云峰1, 潘轩宇1, 陶敏1, 朱贝尔2     
1. 武汉理工大学自动化学院，湖北 武汉 430070;
 2. 远景能源(江苏)有限公司，江苏 江阴 214400
收稿日期: 2014-12-16
作者简介: 徐腊梅（1973-），女，副教授，研究方向为智能控制，E-mail:Lmeix@163.com.
摘要: 研究了高性能能量回馈系统及控制策略；建立了能量回馈系统的数学模型；研究了电流内环、电压外环的双闭环PI控制及基于坐标变换理论的新型数字锁相环；通过Matlab/Simulink软件仿真，验证理论的可行性.最后实验结果验证能量回馈系统理论分析和设计的正确性，并将其应用于无刷双馈电机控制柜中.
关键词： 无刷双馈电机     能量回馈系统     PLL锁相环     Simulink仿真    
Research on energy feedback system based on 90 kW brushless doubly-fed generation system
XU Lamei1, PENG Jian1, XU Yunfeng1, PAN Xuanyu1, TAO Min1, ZHU Beier2     
1. School of Automation,Wuhan University of Technology,Wuhan 430070,China;
 2. Envision Energy (Jiangsu) Limited,Jiangyin 214400,China
Abstract: This paper researches on a high-performance energy feedback system and its control strategy. Firstly, the mathematical model of the energy feedback system is established. Then we research the inner current loop and outer voltage loop PI control and on the new digital phase-locked-loop based on coordinate transformation theory. Afterwords, we create a model of the system in Matlab/Simulink software to verify the feasibility of the theory. Finally, the experimental results are used to verify the correctness of theoretical analysis; and the energy feedback system is used in the BDFM control cabinet.
Key words: BDFM     energy feedback system     digital phase-locked-loop     Matlab/Simulink    

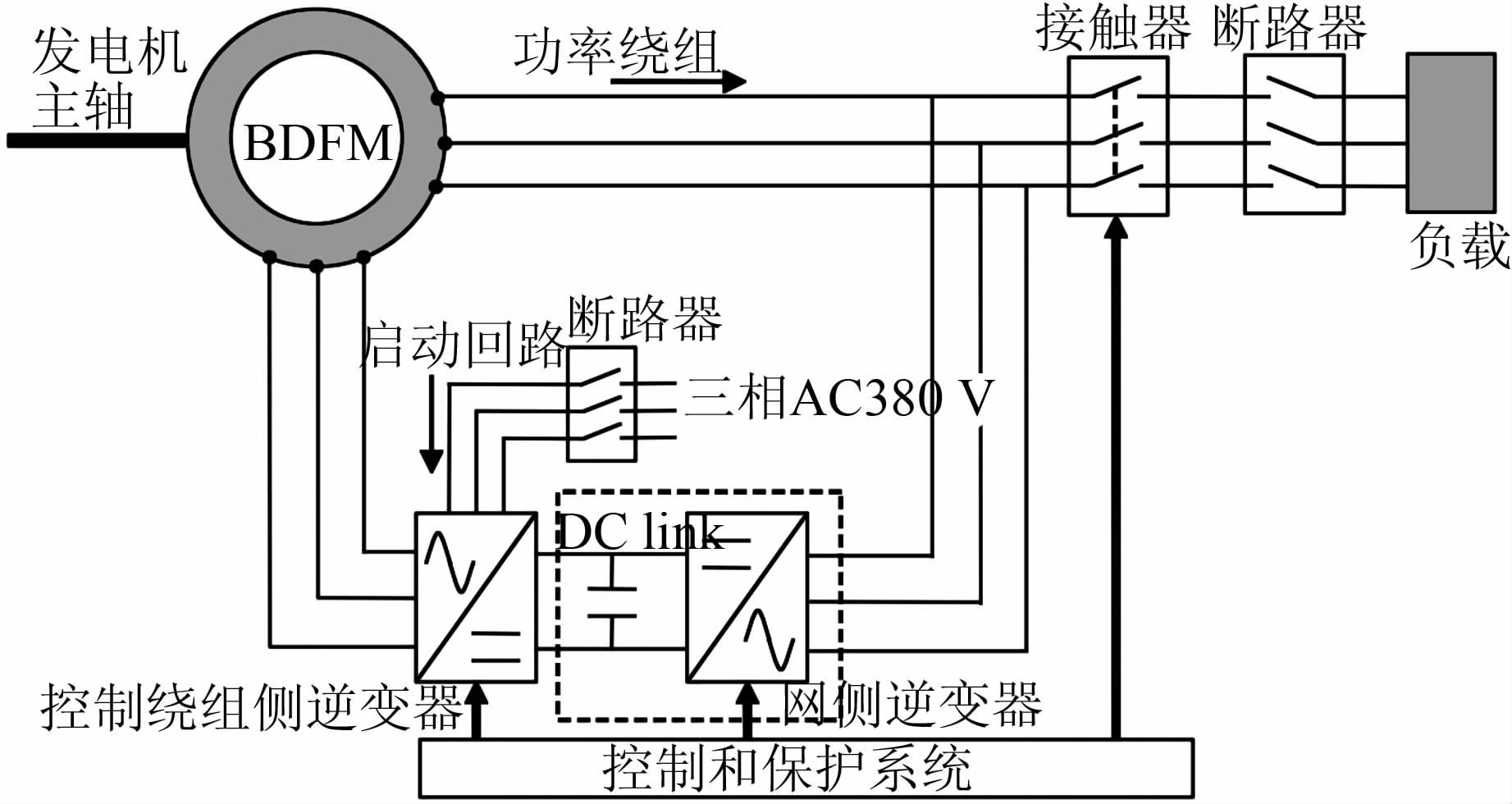
近年来，电力用户对安全、环保、可控、高质量的电能需求不断增长.由于常规能源储备的日益减少，人们越来越注重对于风能等绿色能源的重复开发利用.目前最适用风力变速恒频发电的是交流励磁双馈发电机，其结构类似于绕线式异步电机，当风速变化引起转速变化时，通过控制转子电流的频率，可实现变速恒频控制[1].传统的双馈电机有电刷、滑环的转子结构，系统的可靠性大大降低，维修也不方便.为了克服上述缺点，近些年来出现了一种无刷的双馈变速恒频发电系统[2].无刷双馈发电机运行时，原动机提供功率输入，当转速较低时可以由控制绕组端提供一部分能量，保证功率绕组端电压恒定.无刷双馈发电机的控制绕组用作交流励磁绕组，功率绕组用于发电.原动机转速较高时，可由功率绕组端和控制绕组端同时向电网馈能[3]，其工作原理如图 1所示.

图 1 BDFM发电系统原理图 Figure 1 BDFM power system schematics
图选项

根据BDFM(无刷双馈电机)的相应拓扑结构，可以建立BDFM系统的数学模型，为系统的动态仿真和控制策略的设计提供基础.得益于BDFM的结构特性，异步电机的控制方法也可以用于无刷双馈电机的控制方法中[4]：标量控制，算法简单，但是动态性能指标较低；直接转矩控制[5]，通过直接计算和跟踪磁通和转矩的大小来控制PWM，有较好的动态和静态性能；矢量控制[6]，与异步电机的矢量控制相类似，可以实现对电机转矩、无功功率和有功功率的有效控制；模糊控制[7]，设计相应的模糊功率因数控制方法，确立相应的模糊控制规则，对功率绕组的功率因数进行控制.本文发电系统采用的是矢量控制方式，研究系统中的三相电压型能量回馈环节，如图 1中虚线部分所示.

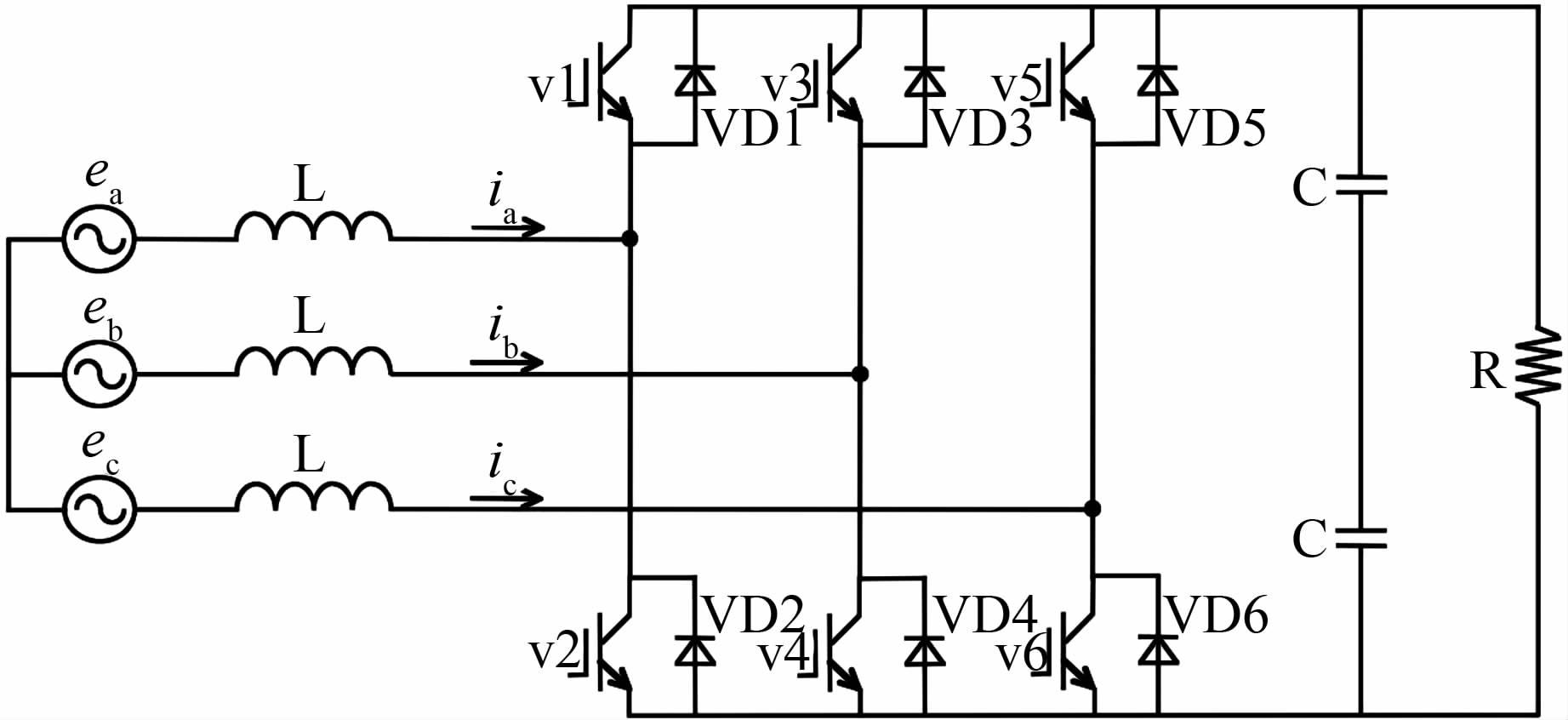
1 三相电压型能量回馈系统 1.1 三相电压型能量回馈系统的拓扑结构

目前，最基本的能量回馈系统分成两个大类：电压型和电流型.其中，电压型能量回馈系统有个明显的特点就是直流侧一般都采用电容进行直流储能，这样一来就使得其直流侧呈现低阻抗电压源特性，其拓扑结构如图 2所示.

图 2 三相电压型能量回馈系统拓扑结构 Figure 2 Three-phase voltage-type energy feedback system
图选项
1.2 三相电压型能量回馈系统的数学模型

要研究三相电压型能量回馈系统，首先要利用电路基本定律对系统在某一参考系下建立数学模型，并且对系统做以下假设：电网电动势为三相平衡的正弦波电压；网侧的滤波电感L始终是线性的，不考虑饱和的情况；系统的能量损耗来自于开关管的开关及其等效串联的导通电阻，不考虑网侧的电阻.

根据三相电压型能量回馈系统的特性分析需要，一般对桥臂开关器件的PWM信号的数学模型可以采用开关函数描述，并且适合用于三相电压型能量回馈系统的波形仿真.

图 2中每一相桥臂的两个开关器件工作于互补状态，这样在不同时刻，参与工作的每相电路就被分成了上管导通和下管导通两种状态.由于每相桥臂有两种开关模式，因此三相能量回馈系统有8种开关模式，定义单极性二值逻辑开关函数：

${{S}_{k}}=\left\{ \begin{matrix} 1,上桥臂导通，下桥臂关断 \\ 0,上桥臂关断，下桥臂导通 \\ \end{matrix} \right.$    (1)

式中：k为a,b,c(a,b,c为三线相连的IGBT功率管).

假设三相电网电压对称稳定，即：

${{e}_{a}}+{{e}_{b}}+{{e}_{c}}=0~,{{i}_{a}}+{{i}_{b}}+{{i}_{c}}=0~$    (2)

根据基尔霍夫电流电压定律，以交流侧电感电流和直流侧电容电压为状态量，可以得到三相静止坐标系下的电压方程为

$\left\{ \begin{array}{*{35}{l}} L\frac{\text{d}{{i}_{\text{a}}}}{\text{d}t}={{e}_{\text{a}}}-R{{i}_{\text{a}}}+\frac{{{u}_{\text{dc}}}(\text{-}2{{S}_{\text{a}}}+{{S}_{\text{b}}}+{{S}_{\text{c}}})}{3} \\ L\frac{\text{d}{{i}_{\text{b}}}}{\text{d}t}={{e}_{\text{b}}}-R{{i}_{\text{b}}}+\frac{{{u}_{\text{dc}}}({{S}_{\text{a}}}-2{{S}_{\text{b}}}+{{S}_{\text{c}}})}{3} \\ L\frac{\text{d}{{i}_{\text{c}}}}{\text{d}t}={{e}_{\text{c}}}-R{{i}_{\text{c}}}+\frac{{{u}_{\text{dc}}}({{S}_{\text{a}}}+{{S}_{\text{b}}}-2{{S}_{\text{c}}})}{3} \\ C\frac{\text{d}{{u}_{\text{dc}}}}{\text{d}t}={{i}_{\text{a}}}{{S}_{\text{a}}}+{{i}_{\text{b}}}{{S}_{\text{b}}}+{{i}_{\text{c}}}{{S}_{\text{c}}}-{{i}_{load}} \\ \end{array} \right.$    (3)

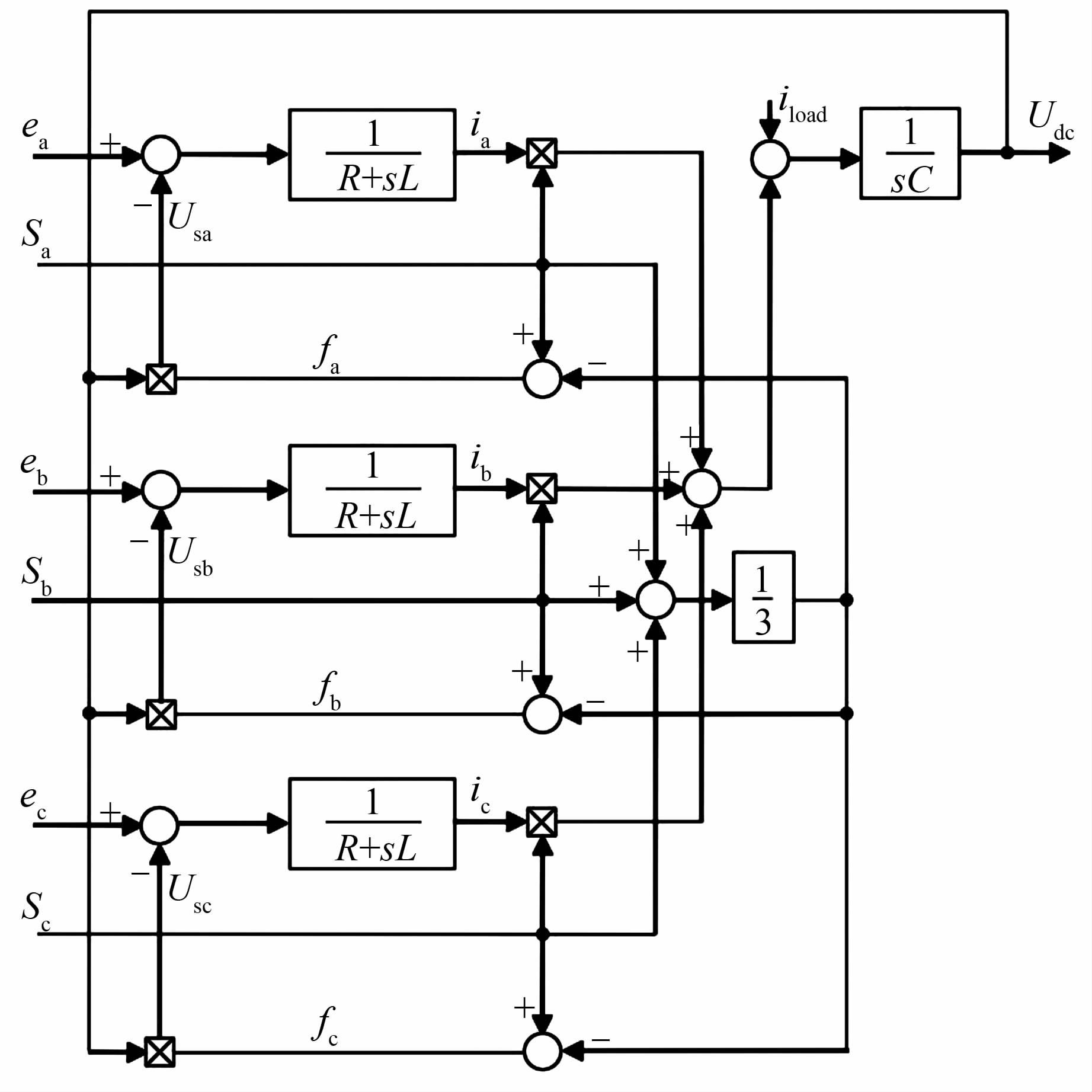
由上式可知，三相输入电流和直流输出电压均与三相开关函数S相关.其中，每相输入电流除了与本相桥臂的开关函数相关，还与其他两相桥臂的开关函数有关，由此可以看出三相电压型能量回馈系统是个三相相互耦合的系统，通过以上两个方程可以得到三相能量回馈系统的数学模型，如图 3所示.

图 3 三相电压型能量回馈系统的数学模型 Figure 3 Mathematical model of the three-phase voltage-type energy feedback system
图选项

其中：

$\left\{ \begin{align} & {{f}_{a}}=\frac{2{{s}_{a}}-{{s}_{b}}-{{s}_{c}}}{3} \\ & {{f}_{b}}=\frac{2{{s}_{b}}-{{s}_{a}}-{{s}_{c}}}{3} \\ & {{f}_{c}}=\frac{2{{s}_{c}}-{{s}_{a}}-{{s}_{b}}}{3} \\ \end{align} \right.$    (4)

在三相abc静止坐标系的数学模型中，三相电压型能量回馈系统交流侧均为具有一定频率、幅值和相角的正弦时变交流量.一般的三相电压型能量回馈系统采用电压电流双闭环控制，当电流内环采用PI调节时，三相静止坐标系中的PI调节器无法实现电流无静差控制.为此，可以通过坐标变换将三相abc静止坐标系转换成以电网基波频率同步旋转的dq坐标系.通过这种坐标变换，静止坐标系中的基波正弦量将转换成同步旋转坐标系中的直流量，对直流给定PI闭环调节器则可以实现无静差控制，从而提高了稳态电流控制精度.同时，由于旋转坐标系中有功电流和无功电流的解耦，更易于实现三相电压型能量回馈系统的有功和无功的独立控制.

为使三相abc静止坐标系转换成两相dq同步旋转坐标系，首先可将三相abc静止坐标系转换成两相αβ静止坐标系，然后在此基础上，转换成两相dq同步旋转坐标系.

按照上述方法，可以得到坐标系的变换矩阵，分别为

${{T}_{abc\to \alpha \beta }}=\frac{2}{3}\left( \begin{matrix} 0 & \frac{\sqrt{3}}{2} & \frac{\sqrt{3}}{2} \\ 1 & \frac{1}{2} & \frac{1}{2} \\ \end{matrix} \right)$    (5)
${{T}_{abc\to dq}}=\frac{2}{3}\left( \begin{matrix} \text{sin}\omega t & \text{sin}\left( \omega t-\frac{2\pi }{3} \right) & \text{sin}\left( \omega t+\frac{2\pi }{3} \right) \\ \cos \omega t & \text{cos}\omega t\left( -\frac{2\pi }{3} \right) & \text{cos}\left( \omega t+\frac{2\pi }{3} \right) \\ \end{matrix} \right)$    (6)

将式(5)、(6)代入式(3)中并简化，得两相αβ静止坐标系和两相dq同步旋转坐标系中的三相电压型能量回馈系统开关数学模型分别为

$\left\{ \begin{align} & L\frac{d{{i}_{\alpha }}}{dt}+R{{i}_{\alpha }}={{e}_{\alpha }}-{{u}_{dc}}{{s}_{\alpha }} \\ & L\frac{d{{i}_{\beta }}}{dt}+R{{i}_{\beta }}={{e}_{\beta }}-{{u}_{dc}}{{s}_{\beta }} \\ & C\frac{d{{u}_{dc}}}{dt}=\frac{3}{2}({{i}_{\alpha }}{{s}_{\alpha }}+{{i}_{\beta }}{{s}_{\beta }})-{{i}_{L}} \\ \end{align} \right.$    (7)
$\left\{ \begin{align} & L\frac{d{{i}_{d}}}{dt}-\omega L{{i}_{q}}+R{{i}_{d}}={{e}_{d}}-{{v}_{d}} \\ & L\frac{d{{i}_{q}}}{dt}+\omega L{{i}_{d}}+R{{i}_{q}}={{e}_{q}}-{{v}_{q}} \\ & C\frac{d{{u}_{dc}}}{dt}=\frac{3}{2}({{i}_{d}}{{s}_{d}}+{{i}_{q}}{{s}_{q}})-{{i}_{L}} \\ \end{align} \right.$    (8)

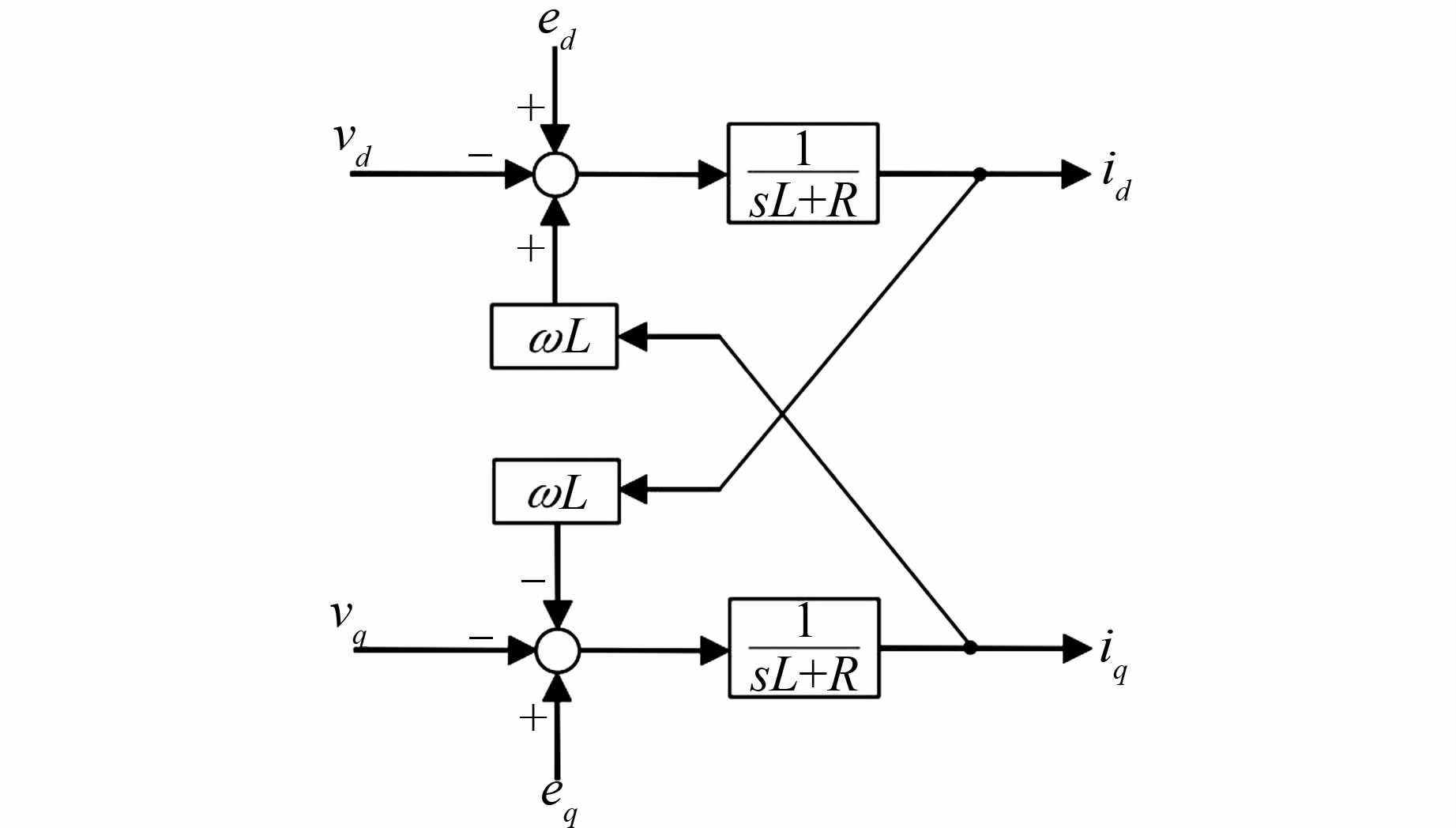
根据上式，可以画出系统在两相dq同步旋转坐标系下的数学模型，如图 4所示.

图 4 dq坐标系下的数学模型 Figure 4 dq coordinate system mathematical model
图选项
1.3 三相电压型能量回馈系统的PI控制设计

三相电压型能量回馈系统正常工作时除了要控制网侧输入电流为正弦波形以外，最重要的目的是稳定直流侧电压udc.因此，通常都是将电压控制环作为双闭环中的外环，而电流控制环作为内环.

1.3.1 三相电压型能量回馈系统的电流内环设计

三相电压型能量回馈系统电流内环经前馈解耦控制后，d轴和q轴电流都等效为一个一阶控制对象，一般采用PI控制器，如果令式(8)中：

$\begin{align} & v{{'}_{d}}=-{{v}_{d}}+{{e}_{d}}+\omega L{{i}_{q}} \\ & v{{'}_{q}}=-{{v}_{q}}+{{e}_{q}}+\omega L{{i}_{d}} \\ \end{align}$    (9)

将式(9)代入方程(8)，可得

$\begin{align} & L\frac{d{{i}_{d}}}{dt}+R{{i}_{d}}=v{{'}_{d}} \\ & L\frac{d{{i}_{q}}}{dt}+R{{i}_{q}}=v{{'}_{q}} \\ \end{align}$    (10)

从上式可以看出，当以v′d和v′q作为等效电流控制变量时，d、q轴电流是独立控制的，相当于对一个一阶系统对象进行控制.等效控制变量v′d和v′q可以由电流环PI调节器输出，可表示为

$\begin{align} & v{{'}_{d}}=({{K}_{iP}}+\frac{{{K}_{iI}}}{s})({{i}^{*}}_{_{d}}-{{i}_{d}}) \\ & v{{'}_{q}}=({{K}_{iP}}+\frac{{{K}_{iI}}}{s})({{i}^{*}}_{_{q}}-{{i}_{q}}) \\ \end{align}$    (11)

由此，可以得到系统在dq坐标系中电流内环控制框图,如图 5所示.

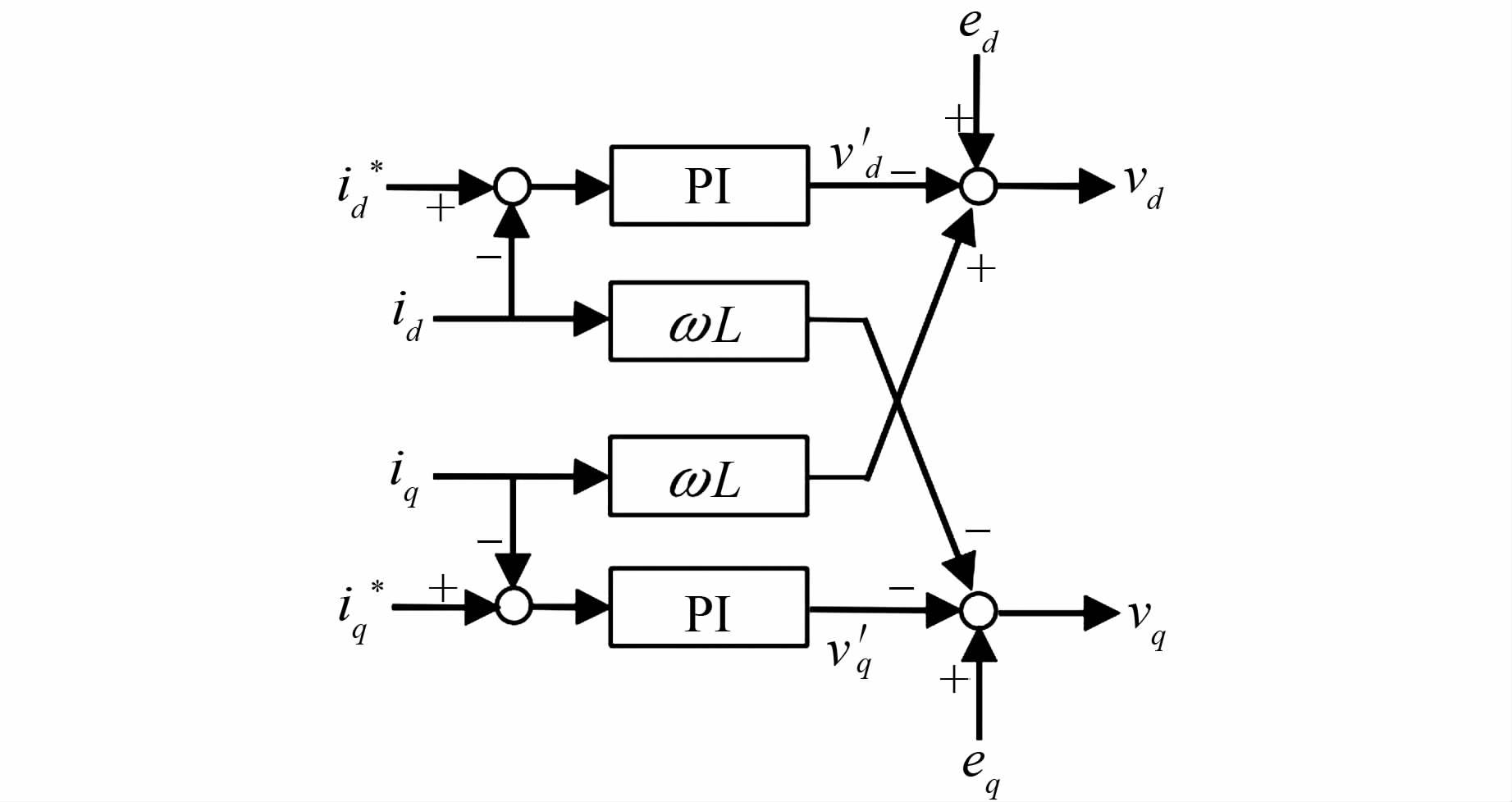
图 5 dq坐标系中电流内环控制框图 Figure 5 dq axis current loop control block diagram
图选项

结合图 4系统的数学模型，本文将解耦控制结构稍作简化，分别得到d轴和q轴电流的等效简化控制结构，以d轴电流控制为例，其等效简化控制结构如图 6 所示.

图 6 d轴电流等效简化控制结构 Figure 6 d-axis current equivalent control structure
图选项

在电流内环控制器设计中，利用内部模型控制方法，可以得到相关的电流控制PI参数：

${{k}_{iP}}={{\alpha }_{i}}L~,{{k}_{iI}}={{\alpha }_{i}}R$

其中：αi为想要的带宽，满足αi＜0.2πFs，Fs为开关频率，取值为10 kHz；R=0.1Ω，L=5 mH.计算可得，电流内环PI调节器的比例增益kiP=31.4，积分增益kiI=630.

1.3.2 三相电压型能量回馈系统的电压外环设计

电压外环设计中，考虑到由于电压外环的主要控制作用是稳定三相电压型能量回馈系统的直流电压，故其控制系统整定时，应着重考虑电压环的抗干扰能力.电压控制环结构图如图 7所示.

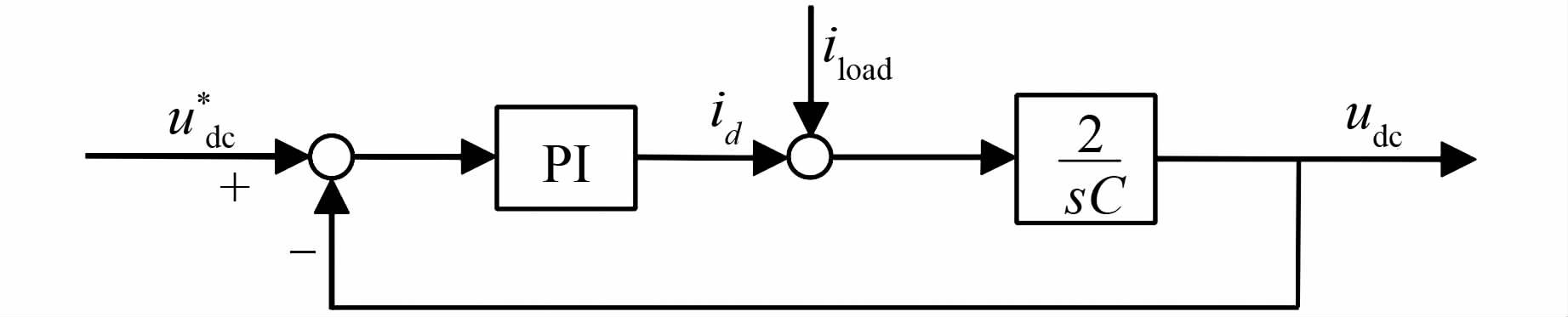
图 7 电压外环控制结构图 Figure 7 Voltage loop control structure
图选项

综合考虑电压环控制系统的抗扰性及跟随性，设定电压外环PI调节器的比例增益kPv=0.5，积分增益kIv=11.

1.4 数字锁相环的结构和控制原理 1.4.1 数字锁相环的结构

针对传统锁相环的缺陷，本文提出一种基于电压矢量变换的测量方法.首先将三相电压变换到两相dq同步旋转坐标系中，然后与锁相环输出构成一个负反馈闭环控制系统，最后通过调节系统参数达到滤波锁相的目的[8].其原理如图 8所示.

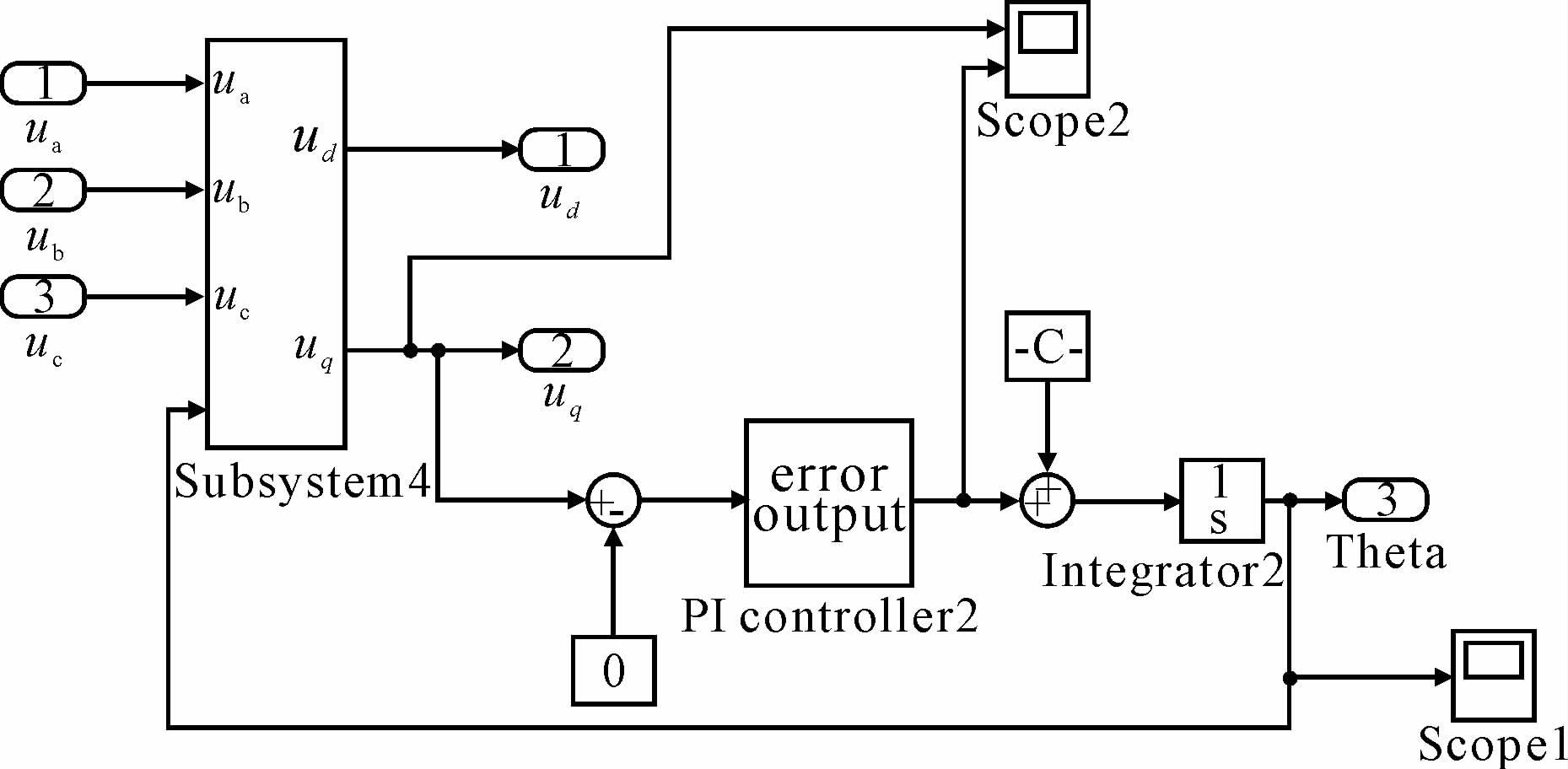
图 8 数字锁相环原理图 Figure 8 Digital phase-locked loop diagram
图选项

首先将三相abc静止坐标系中的电压ua、ub、uc转换成以电网基波频率同步旋转的dq坐标系中的电压分量ud、uq，坐标系转换的依据为式(3)和式(4)的坐标系转换矩阵.其中，坐标变换所用的旋转角θ为锁相环输出量.若锁相角与电网电压不同步，uq进入环路滤波器环节，经过PI调节器后得到误差信号.最后在压控振荡器环节，误差信号和中心频率相加，经过一个积分环节，就得到了相位角θ.

三相不平衡电压经坐标变换后，保证了数字锁相环跟踪的是基波分量，并且能保证快速跟踪输入电压的频率和相位[9].

1.4.2 数字锁相环的控制原理

网侧三相电源电压矢量Uabc=[Ua Ub Uc]T，通过坐标变换矩阵Tabc→dq将三相电网电压转换到两相dq同步旋转坐标系下.

在环路滤波器环节，采用比例-积分型(PI)滤波器，以保证滤波性能和动态系统的稳定性.

在压控振荡器环节，为了得到一个关于锁相环的相位传输函数，压控振荡器模型应该提供一个相位信号θ2.假设压控振荡器的参考频率为常数ω0.由图 2原理图可知，数字锁相环的输出θ(t)为

$\begin{align} & {{\theta }_{2}}(t)=\int_{\text{-}\infty }^{t}{{{K}_{V}}{{u}_{l}}}(\tau )\text{d}\tau \\ & \theta (t)=\int_{\text{-}\infty }^{t}{[{{\omega }_{0}}}+\Delta \omega (\tau )]\text{d}\tau ={{\omega }_{0}}t+\int_{\text{-}\infty }^{t}{{{K}_{V}}{{u}_{l}}}(\tau )\text{d}\tau \\ \end{align}$    (12)

由式(12)得

${{\theta }_{2}}(t)=\theta (t)-{{\omega }_{0}}t$    (13)

因此压控振荡器可以用一个简单的增益为KV的积分器表示，其传输函数为

$G(s)=\frac{\theta (s)}{U(s)}=\frac{{{K}_{V}}}{s}$    (14)
2 基于Matlab/Simulink软件的系统仿真

为了验证电压型能量回馈系统的可行性及性能，利用Matlab/Simulink搭建三相系统模型进行仿真验证.主要参数：三相输入交流电压为380 V，频率50 Hz，三相电网交流侧电阻R=0.1Ω，电感L=5 mH，负载侧串联的两个电容取值为2 400 uF，初始电压270 V.系统总体仿真结构如图 9所示.

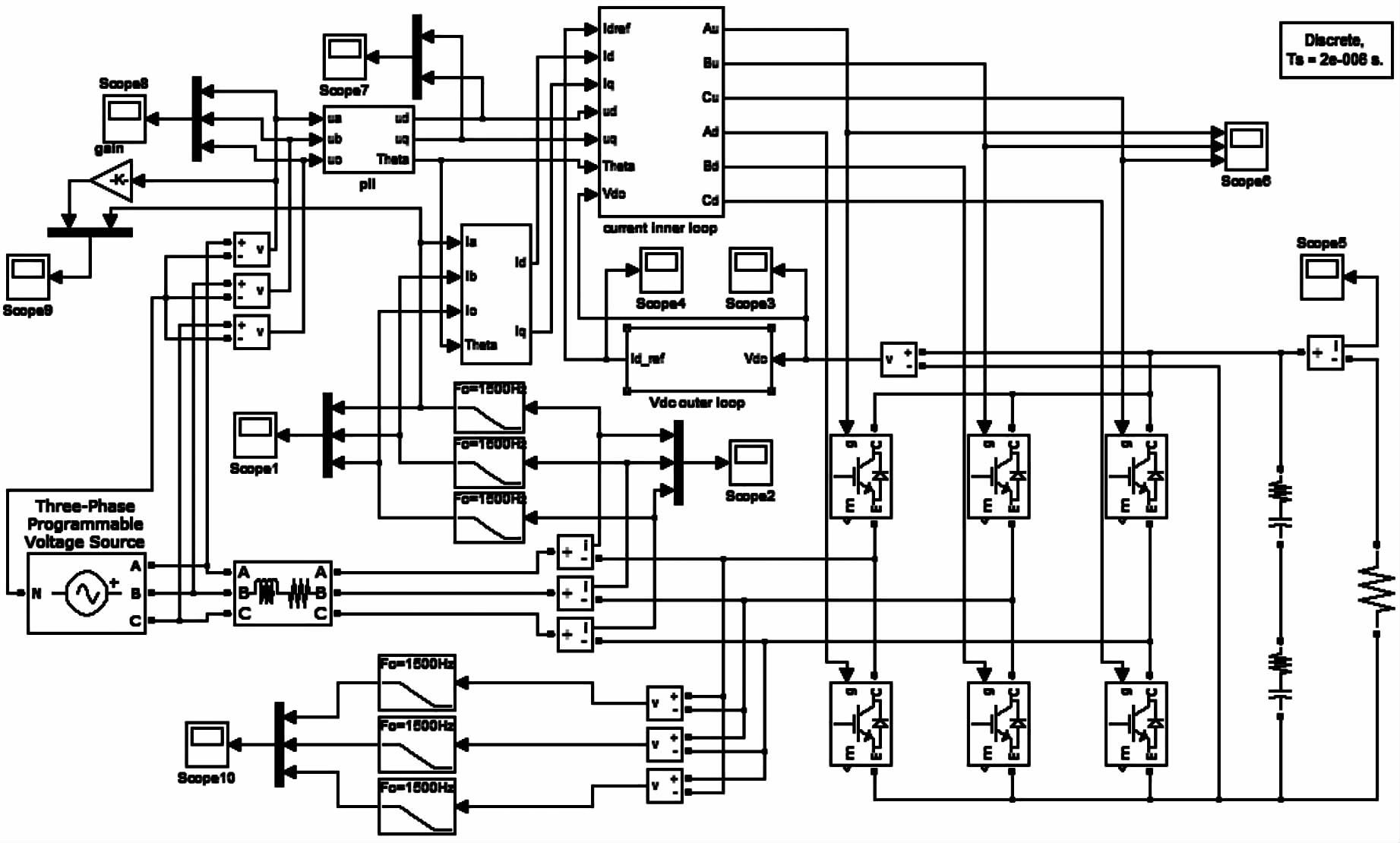
图 9 系统总体仿真结构图 Figure 9 Overall system simulation structure
图选项

通过设置电流内环、电压外环PI调节参数及电路图其他元器件的参数值，可以得到系统输出电压及锁相环的仿真结果如图 10、图 11所示.

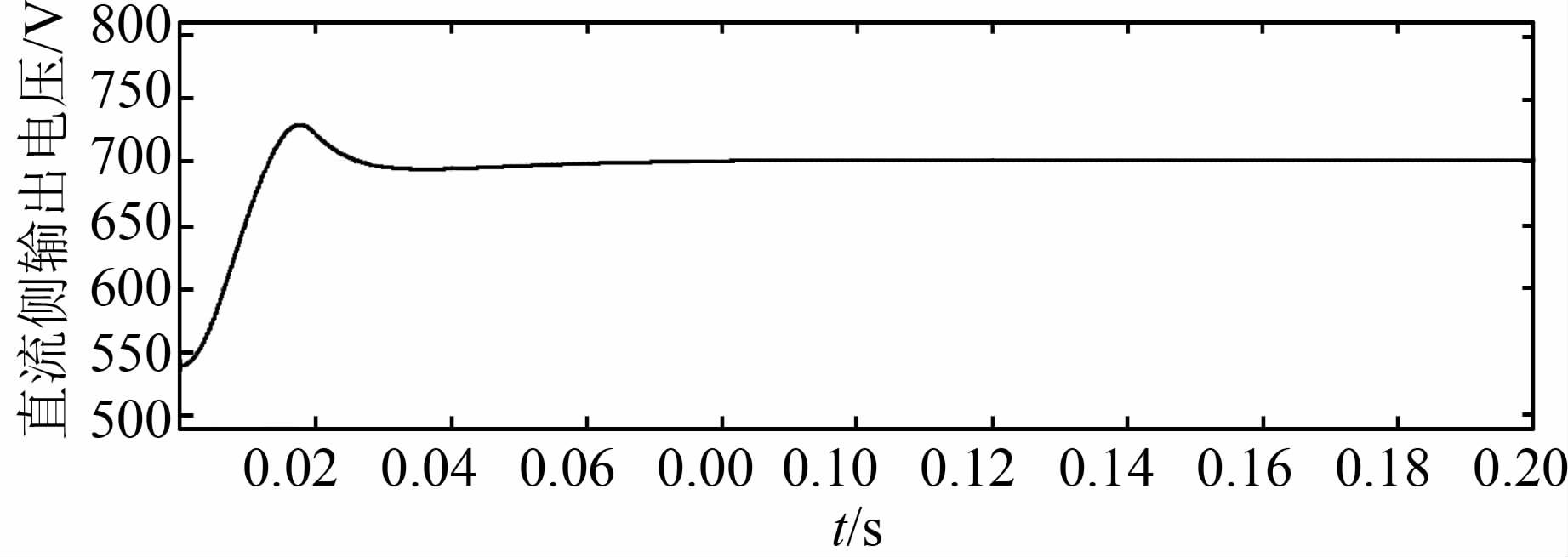
图 10 系统输出电压 Figure 10 System output voltage
图选项
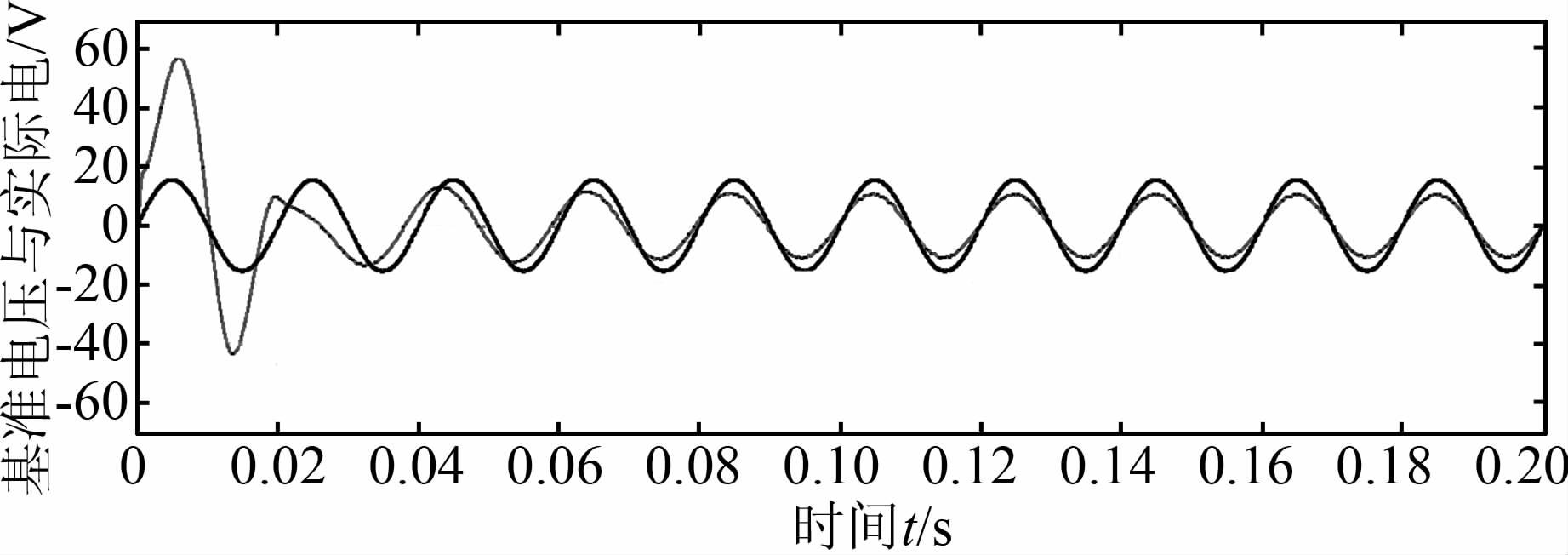
图 11 PLL锁相环仿真结果 Figure 11 PLL simulation results
图选项

由仿真结果看出，系统的上升时间、调节时间都比较短，在经历了短暂的超调后很快回落并稳定在额定输出.数字锁相环的响应时间也很短，在前两个周期时，PI调节器的超调造成了锁相环的不能准确锁相，但是输入信号就很快与输出信号重叠，即输入信号频率相位被锁定，锁相效果良好.

3 实际产品系统调试及实验结果波形

在利用仿真软件进行系统搭建及仿真的基础上，对现有的实际产品(船舶轴带无刷双馈交流发电系统)进行调试.

3.1 系统的静态响应

根据理论参数来设置变频器，运用示波器来采集所需的实验数据，获得实际系统中的直流母线输出电压以及锁相过程中的电流电压波形，如图 12所示.

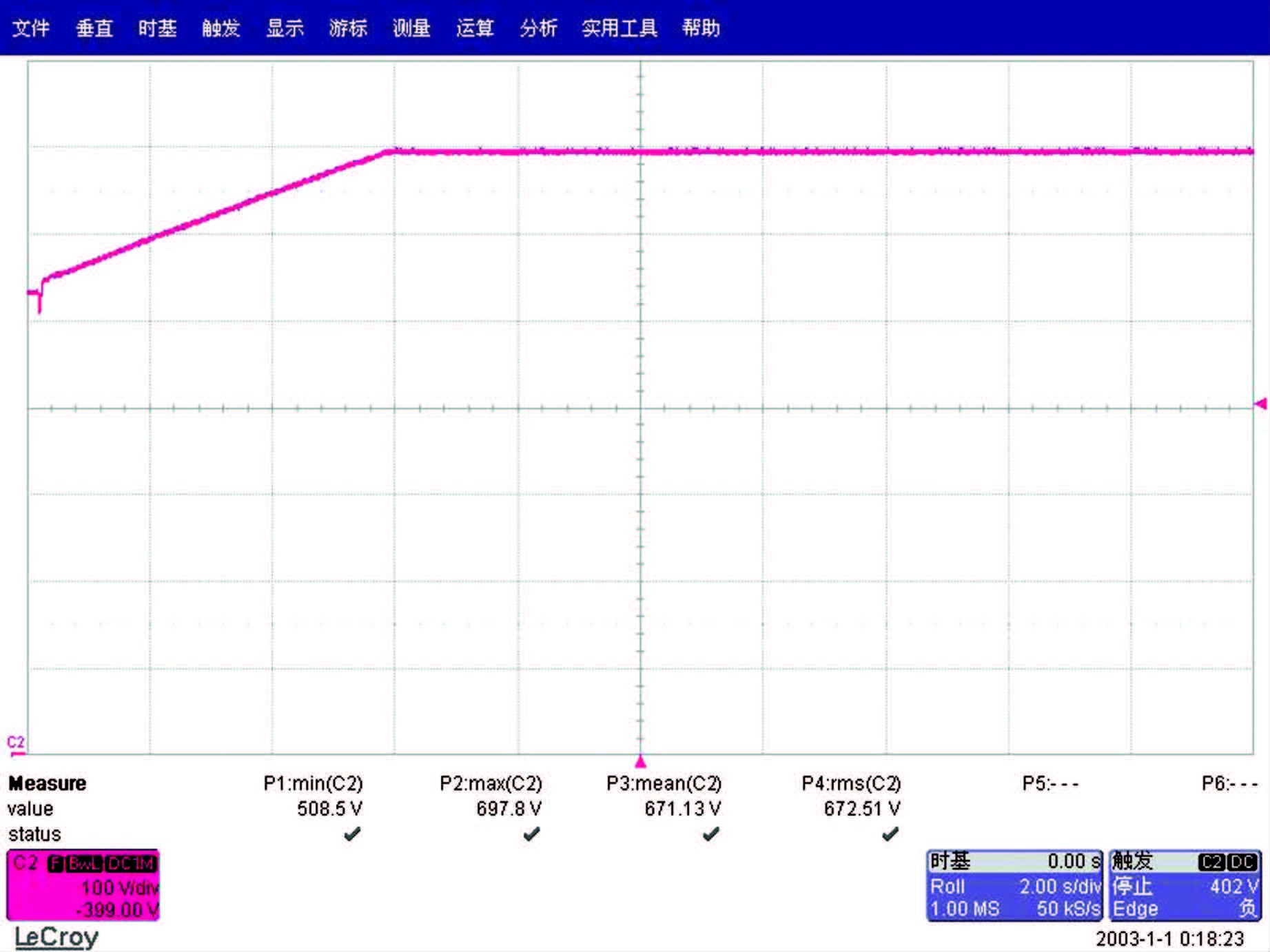
图 12 实际系统的直流母线电压 Figure 12 Actual system DC bus voltage
图选项

整流环节的直流侧输出700 V电压用来给整流与逆变环节之间的DC直流母线电容进行充电，使得在原动机转速较低时，系统可以在短时间内利用电容箱的DC直流电压进行逆变，给功率绕组提供一定的能量，保持功率绕组的电压和频率恒定.

从实验波形可以看出，直流母线电压稳定上升，最后稳定在设定值，波动很小.同时，锁相环作用明显，电流电压相位一致，如图 13，系统工作在单位功率因数整流控制.

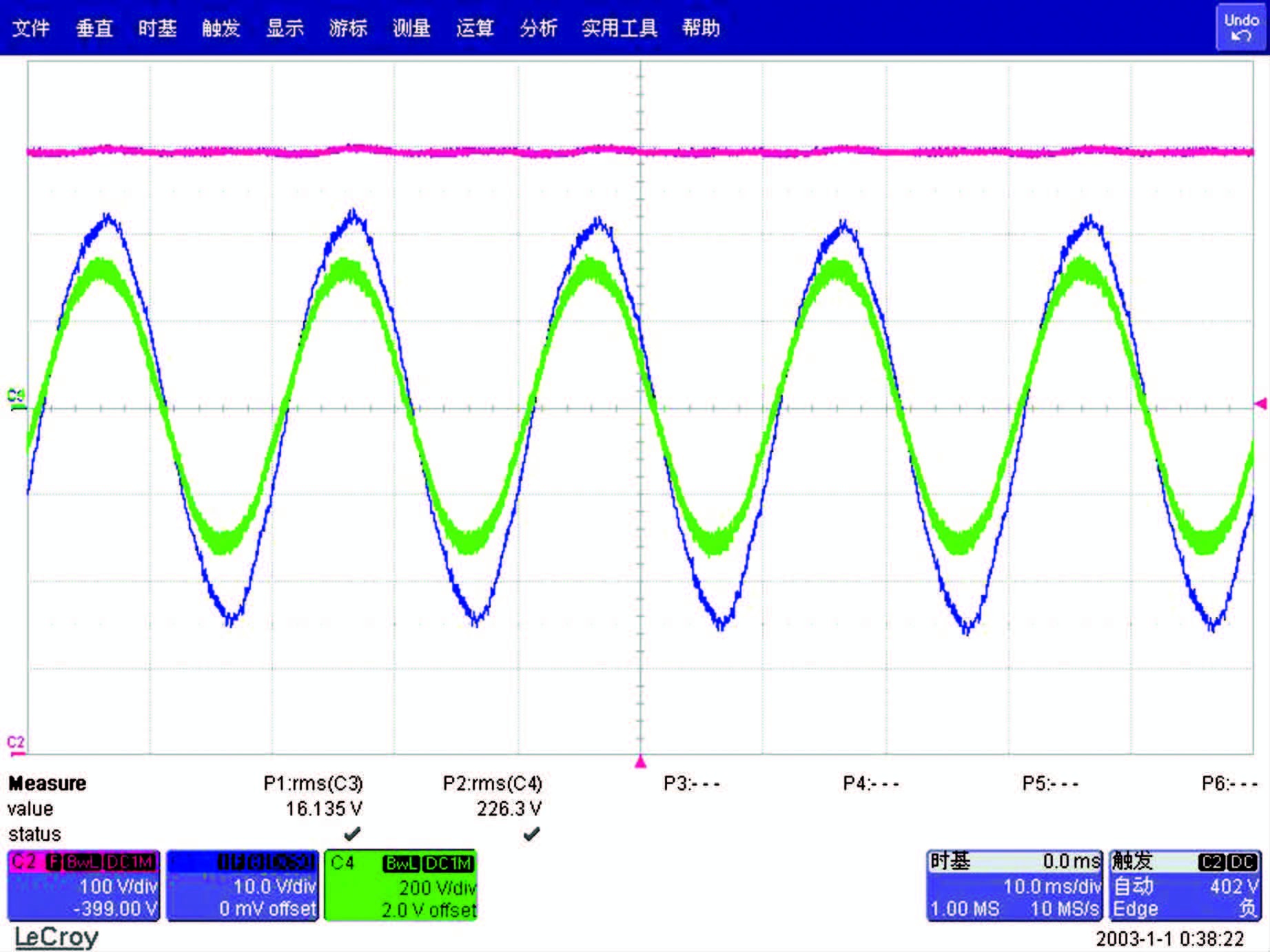
图 13 直流母线电压及电压电流锁相结果 Figure 13 The DC bus voltage and the voltage-current phase lock result
图选项
3.2 系统的动态响应

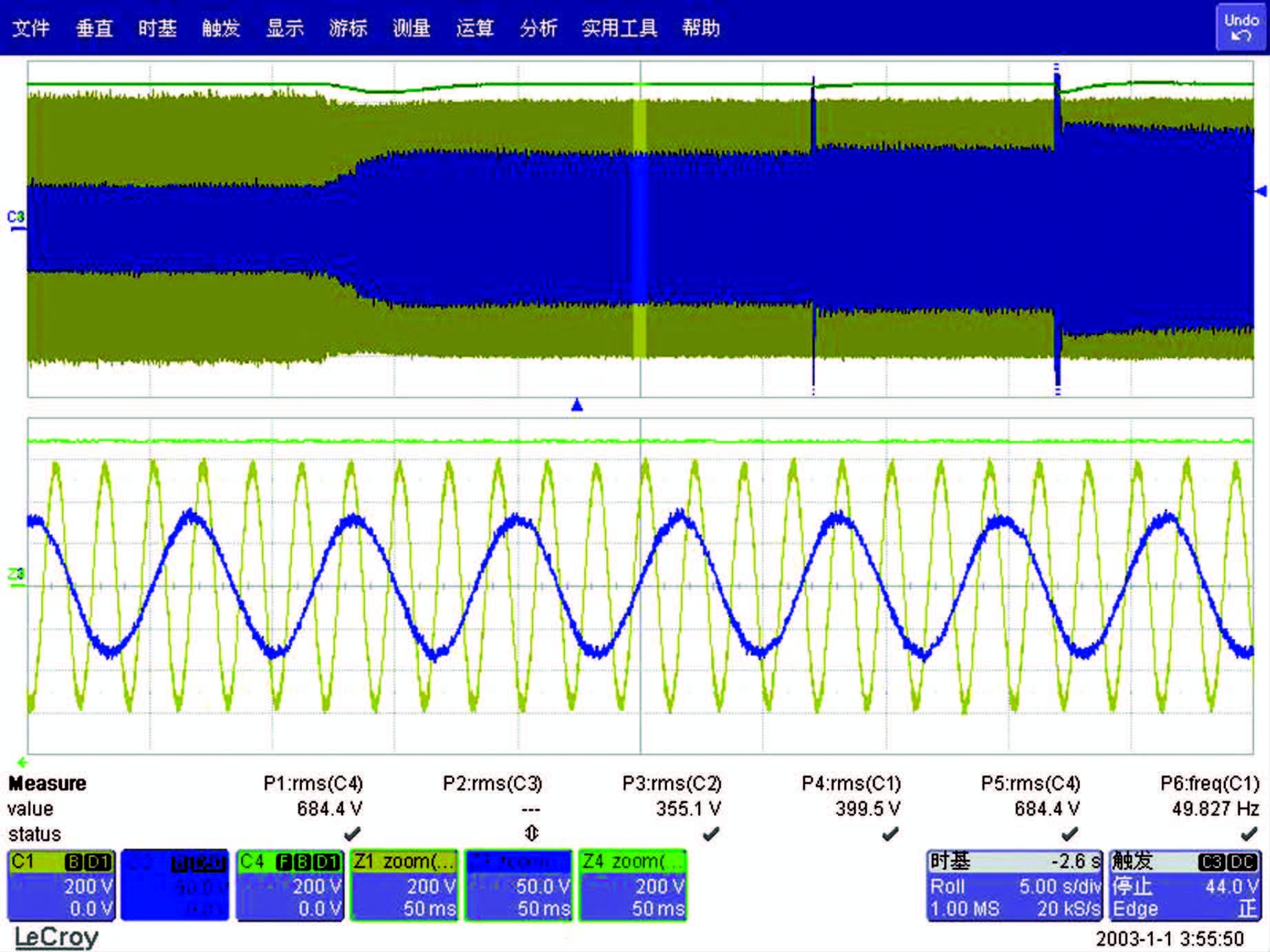
在测试实际系统时，先测试其动态响应，检验系统在突然增加或者撤销小容量负载时的响应.首先，启动无刷双馈发电系统，当系统稳定运行时，依次加入6.4kW电阻负载和7.5 kW以及15 kW电机负载各一台，可得到系统的动态响应波形如图 14所示.稳定运行一段时间后，将所加负载撤销，得到如图 15所示的动态响应波形.

图 14 系统加负载后的动态响应 Figure 14 he system dynamic response under load
图选项
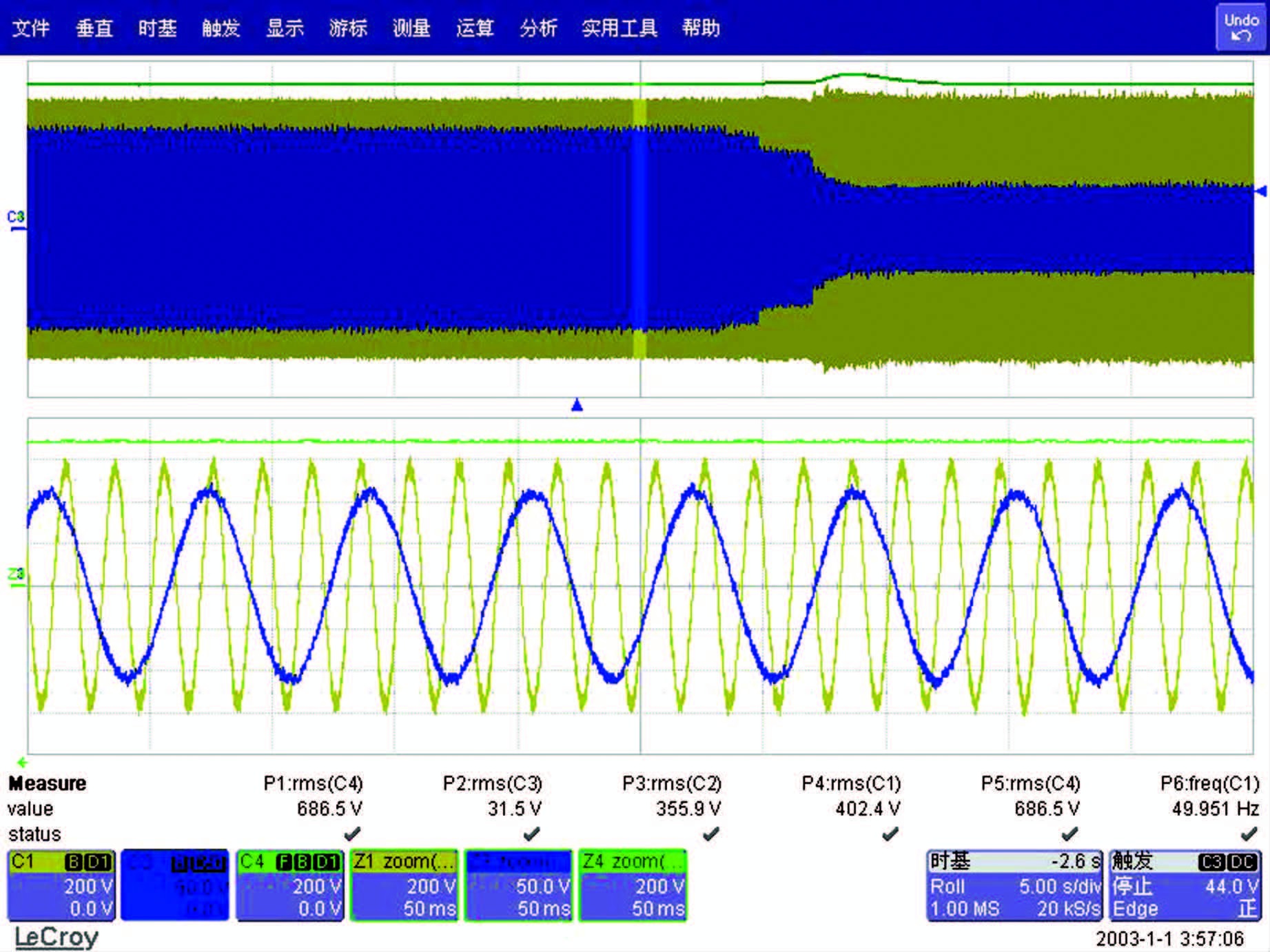
图 15 系统撤负载后的动态响应 Figure 15 Dynamic response after the revocation of the load
图选项

从图中可以看出，系统依次加入3个负载，直流母线电压有小幅的回落，但是很快又上升并稳定在设定值.

系统在撤负载时，直流母线电压有个小幅上升，但很快回落并稳定在设定值，突加突减负载实验说明系统的动态响应良好.

3.3 系统的满功率负载稳定运行

接着测试系统满功率负载运行状态，接入90 kW的负载，系统的运行状态如图 16所示.由图可知，在接入满载90 kW的负载后，系统运行稳定，直流母线电压波动小，电机的控制绕组及功率绕组的电压幅值和频率稳定，能够进行理想的发电运行.

图 16 系统满载运行状态 Figure 16 The running state of the system with full load
图选项
4 总结

本文研究高性能能量回馈系统及控制策略，建立了三相电压型能量回馈系统的数学模型，研究了双闭环PI控制及基于坐标变换理论的新型数字锁相环，接着运用Simulink软件进行了仿真.最后，调试了现有的产品，采集了实际系统的参数波形，验证了理论的准确性和可行性.

参考文献
[1] 彭喜云, 刘瑞叶. 变速恒频双馈风力发电机辅助系统调频的研究[J]. 电力系统保护与控制, 2011, 39(11): 56–61.
Peng Xiyun, Liu Ruiye. Research on the frequency regulation of aidding system of VSCF double-fed wind generator[J]. Power System Protection and Control, 2011, 39(11): 56–61.
[2] Lopez J, Guba E, Sanchis P, et al. Ride through of wind turbines with doubly fed induction generator under symmetrical voltage dips[J]. IEEE Transactions Industrial Electronics, 2009, 56(10): 4246–4254.
[3] 栗然, 唐凡, 刘英培, 等. 双馈式风电场改进的恒电压控制策略[J]. 电力系统保护与控制, 2012, 40(6): 79–85.
Li Ran, Tang Fan, Liu Yingpei, et al. Improved constant voltage control strategy of DFIG based wind farm[J]. Power System Protection and Control, 2012, 40(6): 79–85.
[4] 贾华, 任胜义, 崔军辉. 无刷双馈电机原理及控制策略的发展研究[J]. 电气传动自动化, 2011, 33(1): 37–39.
Jia Hua, Ren Shengyi, Cui Junhui. Development and research of control strategy and the principle for brushless double-fed machine[J]. Electric Drive Automation, 2011, 33(1): 37–39.
[5] 刘伟, 沈宏, 高立刚, 等. 无刷双馈风力发电机直接转矩控制系统研究[J]. 电力系统保护与控制, 2010, 38(5): 77–81.
Liu Wei, Shen Hong, Gao Ligang, et al. Study on direct torque control of brushless doubly-fed machines used for wind power generation[J]. Power System Protection and Control, 2010, 38(5): 77–81.
[6] 李永亮, 赵飞, 王殿俊. 双馈电机矢量控制系统及仿真[J]. 机电元件, 2011, 31(3): 47–50.
Li Yongliang, Zhao Fei, Wang Dianjun. The simulation and vector control system of double-fed machine[J]. Electromechanical Components, 2011, 31(3): 47–50.
[7] 李岚, 栾晓伟. 双馈发电机励磁模糊控制实验研究[J]. 电气技术, 2011(4): 18–21.
Li Lan, Luan Xiaowei. Experimental research of fuzzy control for excitation on doubly-fed induction generator[J]. Electrical Technology, 2011(4): 18–21.
[8] 曹世华, 张维娜, 沈鸿, 等. 新型软件锁相环三相电压型PWM整流器的控制[J]. 电力电子技术, 2008, 42(5): 72–73.
Cao Shihua, Zhang Weina, Shen Hong, et al. Three-phase voltage PWM rectifier control of novel soft phase-locked loop[J]. Power Electronics, 2008, 42(5): 72–73.
[9] 李彦栋, 王凯斐, 卓放, 等. 新型软件锁相环在动态电压恢复器中的应用[J]. 电网技术, 2004, 28(8): 42–45.
Li Yandong, Wang Kaifei, Zhou Fang, et al. Application of soft phase locked loop technique in dynamic voltage restorer[J]. Power System Technology, 2004, 28(8): 42–45.