文章信息
- 孙惠香, 牛欢, 路锋, 刘绍鎏, 张悦
- SUN Huixiang, NIU Huan, LU Feng, LIU Shaoliu, ZHANG Yue
- 弹体斜侵彻混凝土的倾角作用研究
- Research on oblique angle effect during oblique penetration into concrete
- 武汉大学学报(工学版), 2018, 51(12): 1080-1085
- Engineering Journal of Wuhan University, 2018, 51(12): 1080-1085
- http://dx.doi.org/10.14188/j.1671-8844.2018-12-006
-
文章历史
- 收稿日期: 2018-02-10
2. 西安天风建筑安装工程有限公司,陕西 西安 710025
2. Xi'an Tianfeng Construction and Installation Engineering Co., Ltd., Xi'an 710025, China
钻地弹对混凝土结构的侵彻问题是军事防护领域的一个重要研究课题.随着精确制导武器的发展,大型防护工程的战时生存能力遇到重大考验,世界各国在加速发展打击更精确、破坏力更强的钻地弹的同时,也不断地在防护工程领域进行理论论证与实践创新.总体而言,军事防护工程正朝着更大埋深、更高强度发展.
当前对钻地弹侵彻问题的研究以正侵彻为主,Bishop等人最初提出了空腔膨胀理论(Cavity Expansion Theory,CET)[1],经由Goodier改进后,CET广泛应用于刚性弹体的高速侵彻问题[2];20世纪70年代,Bernard根据大量实验数据,利用回归方法,先后提出了弹体侵彻混凝土的侵彻深度计算公式Bernard-A、Bernard-B和Bernard-C;俄罗斯、英国和挪威等各国也相继提出了适用于军事防护领域的侵彻深度经验公式,预测弹体的侵彻能力和防护工程的抗毁伤能力,比较有影响力的有俄罗斯提出的别列赞公式、英国军方提供的英国空军装备规范公式(The Britain Textbook of Air Armament,TBAA)、挪威防护研究院提出的Bergman公式[3, 4].随着计算机技术的发展,ANSYS、ABAQUS、MSA等大型有限元分析软件的应用日趋成熟,研究者对侵彻问题进行了大量的数值模拟,对弹体侵彻混凝土靶体的过程有了更深入的研究.
上述研究主要集中于正侵彻过程,研究弹体参数或靶体材料参数对侵彻效果的影响,但是对斜侵彻问题研究较少,倾角对侵彻效果的影响还需要更深入的研究.考虑实际情形,钻地弹在发射时具有水平方向的初速度,下降过程中获得垂直向下的速度,最终弹体将不可避免地以一定的倾角实现对防护结构的侵彻.正侵彻是一种很理想的侵彻,实际情况下多为非正侵彻,因此有必要研究倾角对侵彻深度的影响,更清晰、更准确地认识钻地弹的侵彻效应.
1 弹体侵彻混凝土过程分析在一般的研究中,可将弹体对混凝土的高速侵彻分为3个阶段,分别是开坑阶段、隧道阶段和后坑阶段[5],如图 1所示.

|
| 图 1 弹体侵彻混凝土的3个阶段划分 Fig. 1 Three stages of penetration into concrete |
开坑阶段发生于弹体与靶体的初始接触阶段,在二者接触瞬间,靶体发生压缩与剪切变形,在靶体的自由表面出现一系列的环向裂纹,随着侵彻的进行,裂纹进一步发展,靶体开始粉碎、迸溅,在弹体撞击处周围形成一个环状弹坑.
如果开坑阶段结束后,弹体仍有足够的动能,将继续向靶体内部运动,这一阶段靶体不再出现大量碎块,而是沿着弹体运动轨迹形成一个直径略宽于弹体直径的隧道,即弹体隧道.如果靶体为半无限大靶体,弹体最终将静止在靶体内部,侵彻过程结束.
考虑到一般防护工程的防护层为有限厚度,弹体可能贯穿靶体,达到侵彻的后坑阶段.在后坑阶段,当弹体临近靶体后表面时,靶体材料会出现碎裂、崩塌现象,在靶体后表面形成一个环状后坑,最后弹体隧道与后坑实现贯通,侵彻过程结束.本文主要考虑半无限大靶体,即侵彻过程不存在后坑阶段.
显然,弹体倾角的影响作用主要体现在开坑阶段.因为在隧道阶段,斜侵彻与正侵彻有着一致的弹靶作用形式,而在后坑阶段,通常认为防护层已经失效,此时主要考虑弹体爆炸对防护结构内部人员与设施的威胁.在开坑阶段,倾角影响弹体与靶体自由表面的接触形式,是计算开坑深度与坑底剩余速度的关键变量.
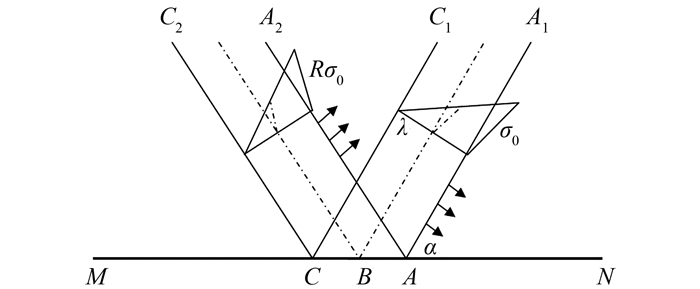
2 斜侵彻深度计算模型建立 2.1 弹体受力计算弹体与靶体接触瞬间,在靶体的自由表面处产生一个应力波,该应力波在撞击界面发生反射,入射波与反射波叠加,对靶体产生破坏作用[6].图 2为接触瞬间在撞击界面入射波与反射波的示意图.
|
| 图 2 应力波在撞击界面的反射 Fig. 2 Reflection of stress wave on free surface |
图 2中:MN为撞击界面,CC1-AA1为入射应力波,CC2-AA2为反射应力波.根据波的反射规律可知:入射应力波与反射应力波的波长相等,令其为λ;倾角与反射角相等,令其为α;反射波波头强度为入射波波头强度的R倍,R为反射系数,是倾角α与靶体材料泊松比υ的函数.假设入射波波头强度为σ0,则反射波波头强度为
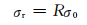 (1)
(1)
其中
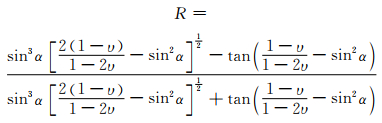 (2)
(2)
Forrestal等[7]对侵彻阻力进行了研究,提出了撞击界面上入射应力波波头强度的表达式为
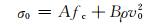 (3)
(3)
式中:fc为靶体材料的单轴抗压强度; ρ为靶体材料的密度; v0为弹体的初速度; A、B为待定系数,可由试验确定.
入射应力波与反射应力波相遇后,任意一点的应力波强度应为入射波与反射波的矢量和.如图 3,任取一点P,假设P点距离入射波波头阵面的距离为l,则P点处入射应力波的强度为
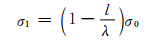 (4)
(4)

|
| 图 3 任意一点处的应力波强度 Fig. 3 Stress wave intensity of an arbitrary point |
反射应力波的强度为
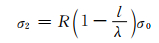 (5)
(5)
根据纵波叠加主应力公式,P点处入射应力波与反射应力波叠加后的主应力为
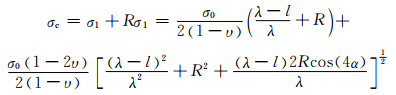 (6)
(6)
主应力σc与撞击界面的夹角为
 (7)
(7)
将式(4)、(5)代入式(7)可得
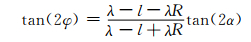 (8)
(8)
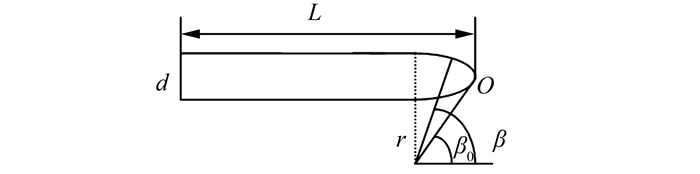
图 4为弹体结构示意图.弹体头部曲率半径为r,弹体直径为d,弹体长度为L.
|
| 图 4 弹体结构示意图 Fig. 4 Structure of projectile body nose |
不考虑弹体头部以外的受力,在弹体头部表面,将任意一点的应力波强度进行面积分.如图 4,弹体在开坑阶段所受阻力可由下式计算[8]:
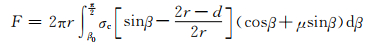 (9)
(9)
由式(6)知,σc为l和λ的函数,根据图 4,l可由下式计算:
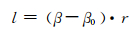 (10)
(10)
根据有限长弹性杆的撞击理论[9],应力波波长λ为
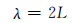 (11)
(11)
其中:L为弹体的长度.
Forrestal等认为,侵彻开坑深度为弹体直径的2倍[10].在斜侵彻条件下,假设弹体直径为d,则开坑深度为
 (12)
(12)
根据侵彻过程的能量守恒,开坑阶段中弹体动能的损失与侵彻阻力在这一过程中做功相等,即
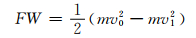 (13)
(13)
其中:v0为弹体初始速度; v1为弹体的坑底剩余速度.
由此可得开坑阶段结束后,弹体在坑底的剩余速度为
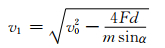 (14)
(14)
开坑阶段结束后进入隧道阶段,将斜侵彻条件下的隧道阶段考虑为倾角α方向上的正侵彻.Bernard等根据微分面力模型假定作用在弹体上的力,得到了正侵彻情况下侵彻深度计算公式[4]:
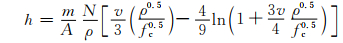 (15)
(15)
其中:A为弹体横截面面积; N为弹头形状系数, 对于卵形弹头
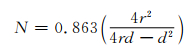 (16)
(16)
v为正侵彻初始速度,即坑底剩余速度
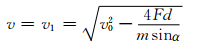 (17)
(17)
将开坑阶段与隧道阶段结合起来,得到斜侵彻的最终弹道长度为
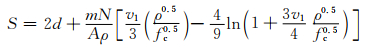 (18)
(18)
根据倾角为α时侵彻深度与弹道长度的几何关系,可得斜侵彻的最终侵彻深度为
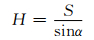 (19)
(19)
在ANSYS/LS-DYNA中对弹体的斜侵彻过程进行数值模拟.弹体模型参照美制GBU-24B型钻地弹[11].弹体直径为475 mm,弹体质量为894 kg,弹体长度为2.50 m,弹体战斗部长度为97.3 cm,战斗部曲率半径为242 cm.混凝土模型参照普通混凝土,抗压强度为30 N/mm2,密度为2 400 kg/m3.建立长10 m、宽10 m、厚20 m的混凝土几何模型,并定义非反射边界条件和非反射对称约束,可以充分模拟半无限厚度靶体.对模型进行网格划分时,因为主要考虑弹体头部受力,弹体头部网格划分较细.靶体的破坏主要发生在接触面周围,故靶体边缘部分网格划分较为粗略.考虑到弹体与靶体的对称性,建立几何模型如图 5所示.

|
| 图 5 几何模型 Fig. 5 Geometric model |
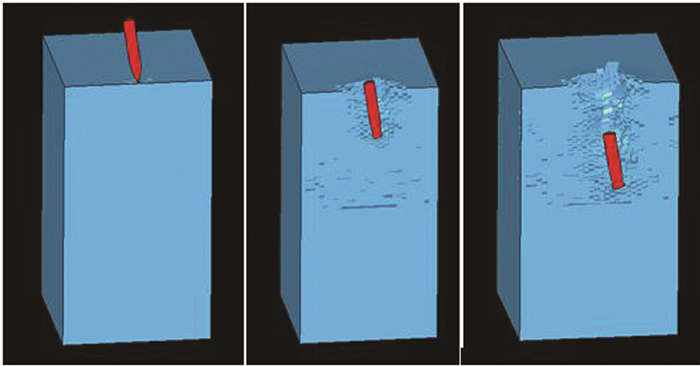
弹体材料选用PLASTIC KINEMATIC模型[12],混凝土材料选用JOHNSON HOLMQUIST CONCRETE模型[13].着弹速度设为500 m/s,倾角为12°,分析时长为2×104 μs,时间步长为100 μs.模拟结果如图 6所示,弹体最终静止在靶体内,可以观察到明显的靶体脱落成坑现象和隧道阶段的弹道.
|
| 图 6 数值模拟弹体斜侵彻效应示意图 Fig. 6 Sketch diagram of numerical simulation |
在LSPREPOSTD后处理器中对模拟结果进行观察.任取弹体上一点,可得侵彻过程中该点在y方向的速度和位移,如图 7、8所示.
|
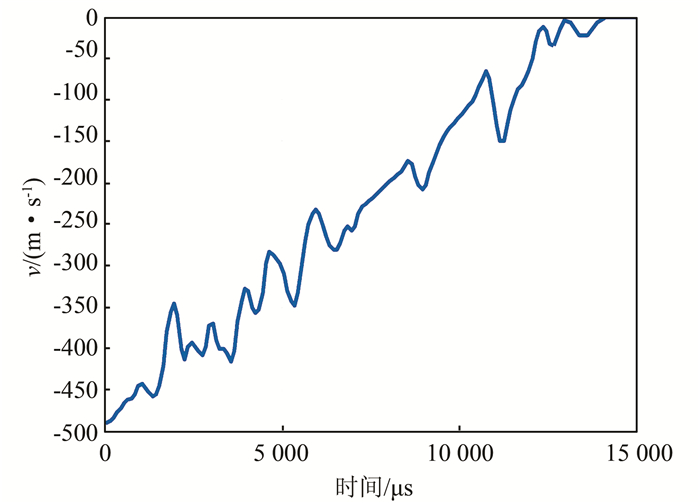
| 图 7 弹体在y方向上的速度变化 Fig. 7 Evolution of y-displacement of projectile |
|
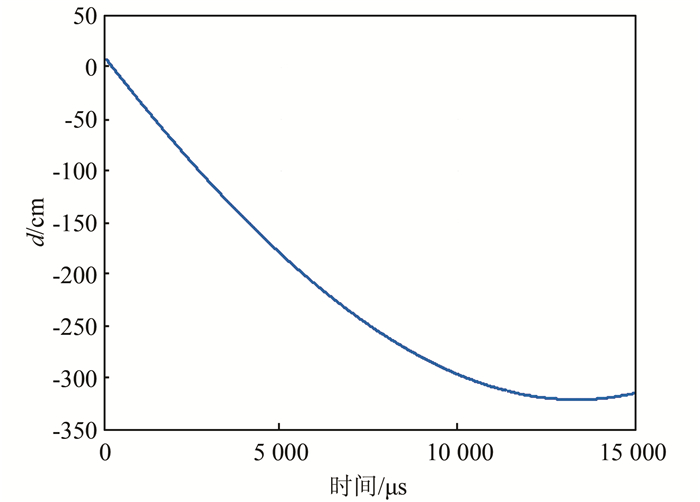
| 图 8 弹体在y方向上位移(侵彻深度)的变化 Fig. 8 Evolution of y-velocity of projectile |
由图 7可知,在侵彻过程中弹体在y方向上的速度随时间呈整体递减趋势,在局部存在震荡,约在13 000 μs时速度减为0,侵彻过程结束.由图 8可知,弹体在y方向上的位移(垂直位移即侵彻深度)随侵彻时间的增大而增速放缓,约在13 000 μs时达到最大侵彻深度,最大侵彻深度约为3.2 m.随后弹体位移出现微量回弹,这一现象是由弹道末端混凝土材料的变形恢复引起的,但对最终侵彻深度影响很小.
3.2 公式验证与修正为了验证理论模型的正确性并研究倾角对侵彻深度的影响,改变倾角的大小,对侵彻过程分别进行数值模拟和理论计算,将结果进行对比.为了避免出现跳弹现象,取倾角α=10°~50°[14].结果如表 1所示.
| 倾角/(°) | 侵彻深度/m | |
| 理论计算 | 数据模拟 | |
| 10 | 3.51 | 3.44 |
| 20 | 3.32 | 3.10 |
| 30 | 3.06 | 2.72 |
| 40 | 2.53 | 2.28 |
| 50 | 1.77 | 1.43 |
将上述数据在Matlab中用3次曲线进行拟合,得到图 9.
|
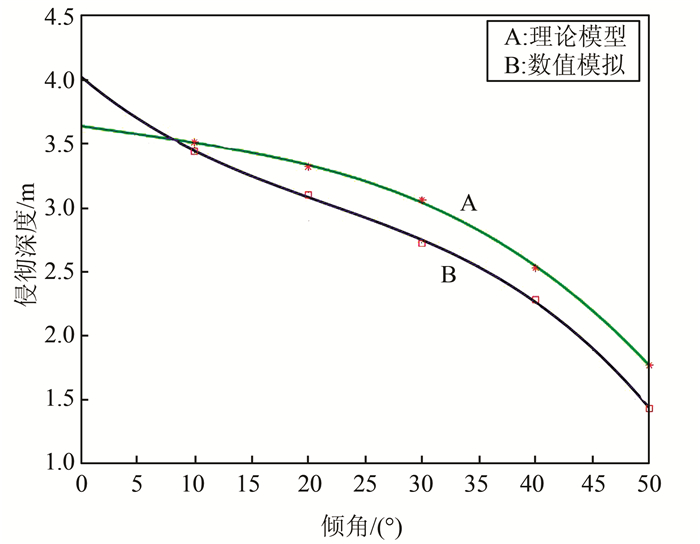
| 图 9 理论计算结果与数值模拟结果的对比 Fig. 9 Comparison between theory model and numerical simulation |
如图 9所示,A线表示理论计算得到的相同条件下侵彻深度随着倾角增大的变化规律.易知随着倾角增大,侵彻深度减小,且倾角越大,侵彻深度减小的速度越快,即倾角越大对侵彻深度的影响越大.当倾角增大到50°时,侵彻深度逐渐接近开坑深度,说明在本例中,当倾角达到50°以上时,容易发生跳弹现象.
B线为数值模拟方法计算得到的相同条件下侵彻深度随着倾角增大的变化规律.对比A线与B线,理论计算结果与数值计算结果随着倾角增大的变化趋势一致.当倾角大于8°时,数值模拟的结果要小于理论计算的结果,两种方法所得结果存在误差.误差的主要来源有:1)理论模型未考虑弹体头部以外部分的受力,未考虑弹体头部的变形,而数值模拟计算过程中弹体头部发生了形变;2)理论模型未考虑弹体在侵彻过程中的偏航现象.斜侵彻隧道阶段的弹体重力方向与摩擦力方向存在夹角,导致弹道在侵彻过程的隧道阶段出现偏移.
综上所述,本文所建立的理论模型可以正确反映弹体斜侵彻混凝土结构的过程中倾角对侵彻深度的影响规律,但所建立模型存在一定的系统误差,该误差源于建立模型的合理假设.误差值与倾角大小无关,稳定在-0.25 m.经修正后,此理论模型计算结果与数值模拟结果吻合良好.理论模型的适用范围为8°~50°.
针对本文所选取的弹体模型、靶体模型和侵彻条件,根据图 9,对式(19)进行以下修正:
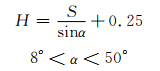 (20)
(20)
本文主要研究了弹体斜侵彻混凝土时倾角对侵彻深度的影响,主要得到以下结论:
1) 根据应力波的反射和传播规律,结合能量守恒定律,研究了倾角、坑底剩余速度和侵彻深度的关系,结合正侵彻经验公式,建立了斜侵彻条件下弹体侵彻混凝土的计算模型,推导了侵彻深度计算公式.
2) 根据侵彻深度计算公式,计算倾角不同时的侵彻深度,结果证明,相同条件下,随着倾角增大,侵彻深度减小;倾角越大,对侵彻过程的影响也越来越显著;倾角增大到一定程度时,会出现跳弹现象.
3) 在ANSYS/LS-DYNA中对弹体的斜侵彻过程进行数值模拟,将模拟结果与理论计算结果进行对比和误差分析,认为误差的主要来源是建立模型过程中对问题的合理假设.根据误差分析对理论模型进行合理修正,并将模型适用条件精确为8°~50°.
| [1] |
欧阳春, 赵国志, 夏卫国, 等. 空腔膨胀理论中混凝土材料模型的对比[J]. 南京理工大学学报, 2005, 6(5): 464-468. Ouyang Chun, Zhao Guozhi, Xia Weiguo, et al. Investigation of material models of concrete used in cavity expansion theory[J]. Journal of Nanjing University of Science and Technology, 2005, 6(5): 464-468. |
| [2] |
陈小伟, 李小笠, 陈裕泽, 等. 刚性弹侵彻动力学中的第三无量纲数[J]. 力学学报, 2007, 39(1): 77-84. Chen Xiaowei, Li Xiaoxia, Chen Yuze, et al. The third dimensionless parameter in the penetration dynamics of rigid projectiles[J]. Chinese Journal of Theoretical and Applied Mechanics, 2007, 39(1): 77-84. |
| [3] |
刘绍鎏, 孙惠香, 张悦, 等. 相似理论与量纲分析法相结合的钻地弹侵彻岩体经验公式[J]. 空军工程大学学报(自然科学版), 2017, 18(3): 99-103. Liu Shaoliu, Sun Huixiang, Zhang Yue, et al. The research on an empirical formula for earth penetrator weapons penetrating rocks targets[J]. Journal of Air Force Engineering University (Natural Science Edition), 2017, 18(3): 99-103. DOI:10.3969/j.issn.1009-3516.2017.03.017 |
| [4] |
任辉启, 穆朝民, 刘瑞朝, 等. 精确制导武器侵彻效应与工程防护[M]. 北京: 科学出版社, 2016. Ren Huiqi, Mu Zhaomin, Liu Ruichao, et al. Penetration Effects of Penetration Guided Weapons and Engineering Protection[M]. Beijing: Science Press, 2016. |
| [5] |
刘先应.高速侵彻混凝土的局部响应行为研究[D].太原: 太原理工大学, 2016. Liu Xianying. Studies on local impact responses of high-speed projectile penetration into concrete target[D]. Taiyuan: Taiyuan University of Technology, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10112-1016714288.htm |
| [6] |
薛建峰, 沈培辉, 王晓鸣. 弹体斜侵彻混凝土靶面的开坑阶段分析[J]. 南京理工大学学报, 2016, 40(1): 72-76. Xue Jianfeng, Shen Peihui, Wang Xiaoming. Analysis of crater-forming of projectile obliquely penetrating into concrete target[J]. Journal of Nanjing University of Science and Technology, 2016, 40(1): 72-76. |
| [7] |
Forrestal M J, Altman B S, Cargile J D, et al. An empirical equation for penetration depth of ogive-nose penetrator into concrete targets[J]. International Journal of Impact Engineering, 1994, 15(4): 395-405. DOI:10.1016/0734-743X(94)80024-4 |
| [8] |
薛建峰, 沈培辉, 王晓鸣. 弹体侵彻混凝土开坑阶段阻力的计算[J]. 高压物理学报, 2016, 30(6): 499-504. Xue Jianfeng, Shen Peihui, Wang Xiaoming. Resistance during cratering for projectile penetration into concrete target[J]. Chinese Journal of High Pressure Physics, 2016, 30(6): 499-504. |
| [9] |
王礼立. 应力波基础[M]. 北京: 国防工业出版社, 1983. Wang Lili. Foundation of Stress Waves[M]. Beijing: National Defend Industry Press, 1983. |
| [10] |
柴传国, 皮爱国, 武海军, 等. 卵形弹体侵彻混凝土开坑区侵彻阻力计算[J]. 爆炸与冲击, 2014, 34(5): 630-635. Chai Chuanguo, Pi Ai'guo, Wu Haijun. A calculation of penetration resistance during cratering for ogive-nose projectile into concrete[J]. Explosion and Shock Waves, 2014, 34(5): 630-635. |
| [11] |
周健南, 金丰年, 王斌. 别列赞公式中弹体参数取值的探讨[J]. 弹道学报, 2008, 20(2): 20-23. Zhou Jiannan, Jin Fengnian, Wang Bin. Discussion on projectile parameters in Береэаиь Formular[J]. Journal of Ballistics, 2008, 20(2): 20-23. |
| [12] |
庞洪鑫.高速侵彻钢筋混凝土靶板的数值模拟研究[D].北京: 北京理工大学, 2015. Pang Hongxin. The study of numerical simulation of high-speed penetration into reinforced concrete[D]. Beijing: Beijing Institute of Technology, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10007-1015030349.htm |
| [13] |
宋梅利, 王晓明, 赵希芳, 等. 弹体高速侵彻混凝土靶侵彻效率影响因素分析[J]. 南京理工大学学报, 2014, 38(3): 390-395. Song Meili, Wang Xiaoming, Zhao Xifang, et al. Influencing factors of penetration efficiency for projectiles' high-speed penetration into concrete targets[J]. Journal of Nanjing University of Science and Technology, 2014, 38(3): 390-395. DOI:10.3969/j.issn.1005-9830.2014.03.015 |
| [14] |
马爱娥, 黄风雷. 弹体斜侵彻钢筋混凝土的试验研究[J]. 北京理工大学学报, 2007, 27(6): 482-486. Ma Ai'e, Huang Fenglei. Experimental research on oblique penetration into reinforced concrete[J]. Transactions of Beijing Institute of Technology, 2007, 27(6): 482-486. DOI:10.3969/j.issn.1001-0645.2007.06.004 |
 2018, Vol. 51
2018, Vol. 51




