文章信息
- 王建群, 焦钰
- WANG Jianqun, JIAO Yu
- 狼群算法的改进及其在水库优化调度中的应用
- Improvement of wolf pack search algorithm and its application to optimal operation of reservoirs
- 武汉大学学报(工学版), 2017, 50(2): 161-167, 173
- Engineering Journal of Wuhan University, 2017, 50(2): 161-167, 173
- http://dx.doi.org/10.14188/j.1671-8844.2017-02-001
-
文章历史
- 收稿日期: 2016-08-10
1975年John Holland提出遗传算法(GA),标志着基于生物学启发的进化算法研究时代的到来[1].随后,众多学者以自然界群体生物生活习性为启发得到了一些各具特色的现代启发式算法或称为群体智能优化算法,例如粒子群算法(PSO)[2]、蚁群算法(ACO)[3]、蜂群算法(ABC)[4]、人工鱼群算法(AFSA)[5]、萤火虫优化算法(GSO)[6]、狼群算法(WPA)[7]等.其中狼群算法(WPA)的思想最早是由Yang等于2007年仿生狼群捕食行为和猎物分配方式而提出的[7], Liu、周强、吴虎胜等均对WPA进行了完善[8-10].Li等将狼群算法用来优化糖尿病患者周围血管闭塞估计模型参数[11];伊廷华等对狼群算法进行了分组改进并用于3维传感器优化布置[12, 13];王建群等将狼群算法应用于水电站优化调度模型求解,计算结果表明狼群算法比基本粒子群算法、基本遗传算法及动态规划具有更高的精度[14].然而,WPA算法过分强调个体的独立性,缺乏群体之间信息的共享及个体对历史经验的认知学习, 当求解比较复杂的多极值点优化问题时效率较低.本文将针对WPA算法的上述不足加以改进,并研究其在水库优化调度中的应用.
1 WPA算法 1.1 基本原理WPA主要通过狼群的游猎竞争、召唤奔袭、围攻猎物、狼群竞争更新等4个主要捕食行为启发式寻优,以算子的变化对狼匹位置进行变更,以目标函数值的优劣来衡量个体狼所处位置的好坏.
WPA的主要计算步骤[14]:
1) 规模大小为N的狼群中,第i匹狼Xi=(xi1, xi2, …, xij, …, xiT)在T维决策空间中第j维的初始位置可以表示为
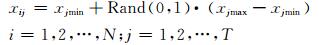 (1)
(1)
式中:Rand(0, 1) 为[0, 1]上均匀分布的随机数;xjmax,xjmin分别为决策变量xi的第j维分量的上限与下限.
2) 在当前狼群中选取1匹领导者狼及L匹竞选狼来统领狼群.竞选狼进行游猎搜索竞争领导者狼:
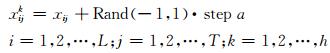 (2)
(2)
式中: Rand(-1, 1) 为[-1, 1]上均匀分布的随机数;step a为游猎搜索步长;xij为第i只竞选狼的当前位置;xijk为第i匹竞选狼向第k个方向搜索产生的位置.
3) 个体狼进行奔袭搜索:
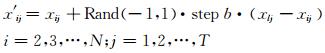 (3)
(3)
式中:Rand(-1,1) 为[-1, 1]上均匀分布的随机数;step b表示奔袭步长;xlj表示头狼所在位置;xij为第i匹狼当前位置;x′ij表示第i匹狼奔袭搜索到的位置,若奔袭搜索到的位置增优,则移动到该位置,否则保持当前位置不变.
4) 个体狼对猎物展开围攻:
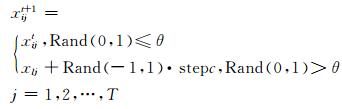 (4)
(4)
式中:xijt+1表示第i匹狼围攻搜索到的位置;xijt表示第i匹狼当前位置;θ为阈值参数;step c为围攻步长:
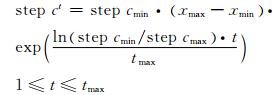 (5)
(5)
式中:t表示当前迭代次数;tmax表示最大迭代次数;step cmax与step cmin分别表示最大与最小包围步长.
5) 若循环迭代终止条件满足,则输出最优解;否则根据“优胜劣汰”的法则对狼群进行更新,淘汰m匹目标函数值较差的狼并随机产生m匹新生狼,转步骤(2).
1.2 WPA算法改进PSO算法根据当前个体极值点与全局极值点进行位置移动,同时利用了个体和群体经验的导向作用,这也正是PSO算法的优良特性之处[15].而基本WPA算法中个体狼在搜索或捕食猎物时,过分强调个体的独立性,个体之间缺乏相互协作机制,导致当个体狼没有找到食物或更好的位置时,采用漫无目的的随机机械运动,缺乏群体之间信息的共享及个体对历史经验的认知学习.当WPA算法的头狼陷入局部极值时,其将带领狼群盲目地向局部极值集中而导致优化效果变差,过早收敛,当求解比较复杂的多极值点优化问题时效率较低.为此,对WPA算法的召唤奔袭算子和围攻猎物算子加以改进,即将式(3)、(4) 改进为
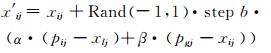 (6)
(6)
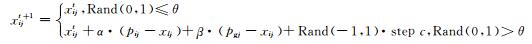 (7)
(7)
式中:pij为第i匹狼迄今为止搜索到的最好位置;pgj为整个狼群迄今为止搜索到的最好位置;α,β分别表示当前个体极值点pij及全局极值点pgj对狼匹行为的指导因子,取为[0, 1]上的随机数.
为验证改进后的新狼群算法(记为NWPA)的优化性能,将通过表 1中4个典型的基准测试函数[16]对NWPA算法进行数值仿真实验,并与WPA算法、PSO算法的寻优精度展开对比分析.
| 函数 | 搜索区间 | 理论最优值 | 维数 |
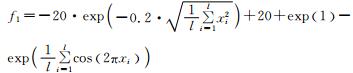 |
xi∈[-32.768, 32.768] | f1(0)=0 | l=30 |
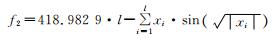 |
xi∈[-500, 500] | 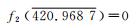 |
l=30 |
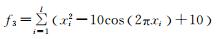 |
xi∈[-5.12, 5.12] | f3(0)=0 | l=30 |
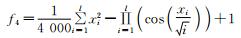 |
xi∈[-60, 60] | f4(0)=0 | l=30 |
试验中,3种算法的群体数量统一选取为100,最大迭代次数均选取为800次;其余参数设置如下:对于NWPA算法、WPA算法,参考文献[9]取:L=5,h=4,step a=1.5,hmax=15,step b=0.9,θ=0.2,step cmax=100 000,step cmin=0.5,m=5;对于PSO算法,参考文献[2]取:c1=2,c2=2,ωmax=1.4,ωmin=0.4.为削弱随机性对测试结果的影响力,本文在实验中依次采取各算法对各基准函数各进行30次独立重复运算,以测试结果的最优值、平均值、标准差为评价指标,评价各算法优化性能及稳定性能的强弱.数值仿真实验结果如表 2所示.
| 基准函数 | 智能算法 | 最优值 | 平均值 | 标准差 |
| f1 | PSO WPA NWPA |
3.401 7.000×10-6 2.300×10-5 |
4.688 7.037×10-5 4.577×10-5 |
5.052×10-1 1.052×10-4 1.719×10-5 |
| f2 | PSO WPA NWPA |
5.922×102 1.273×10-4 1.270×10-4 |
9.620×102 2.204×102 6.712×10 |
2.832×102 1.547×102 7.415×10 |
| f3 | PSO WPA NWPA |
7.358×10 2.885×10 1.000×10-6 |
1.115×102 5.204×10 1.267×10-6 |
2.023×10 1.195×10 4.498×10-7 |
| f4 | PSO WPA NWPA |
8.867×10-1 1.310×10-4 0.000 |
9.859×10-1 2.477×10-4 0.000 |
3.906×10-2 9.250×10-5 0.000 |
此外,为了更直观地了解上述3种算法的寻优精度与收敛速度,本文给出了3种算法在测试上述4个基准测试函数时的收敛曲线对比图,如图 1所示.
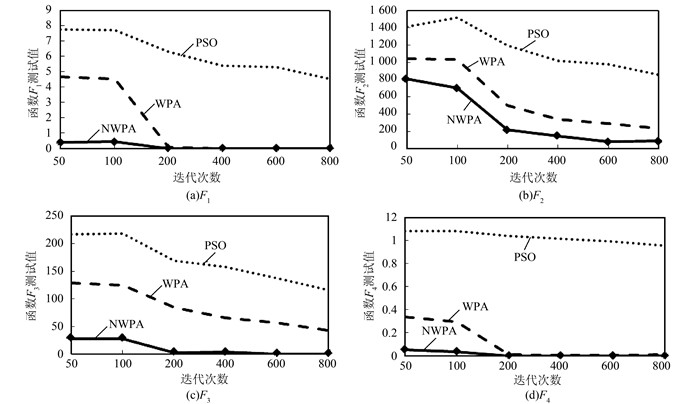
|
| 图 1 收敛曲线对比图 Figure 1 Comparison of convergence curves |
由表 2数值仿真实验结果可知,NWPA算法在求解上述前4个相对复杂的多峰函数时,最优值、平均值2项评价指标的数值均较其他2种算法有明显的下降而更接近理论优值,算法的优化性能有着明显的提升,有效地避免了局部极值;同时标准差对应数值也有着明显的下降,算法的稳定性能较其他2种算法也有着明显的提升.此外,由图 1的收敛曲线对比图可知,NWPA算法较其他2种算法在收敛速度及收敛精度方面均有着明显提升.
2 NWPA算法参数分析NWPA算法共包含10个参数:狼群规模N、竞选狼数目L、游猎搜索方向h、游猎搜索步长step a、最大游猎搜索次数hmax、奔袭步长step b、围攻算法阈值θ、最大围攻步长step cmax、最小围攻步长step cmin、竞争更新淘汰狼数目m.参数的取值设置是智能优化算法中相当重要的步骤,影响着算法的性能.下面采用基于基准函数仿真实验的方法研究其中的step a、step b、θ、step cmax、step cmin 5项敏感性参数的有效取值范围.
实验中,算法各参数的初始值从参考文献[9]中取值:N=100,L=5,h=4,step a=1.5,hmax=15,step b=0.9,θ=0.2,step cmax=100 000,step cmin=0.5,m=5.当对上述参数中的某一参数进行敏感性实验时,其余参数保持以上经验取值不变.
在实验中为削减随机性对测试成果的干扰,本文将采用算法在各种参数取值情况下依次对表 1中的4种函数运行30次独立重复寻优试验,并统计重复寻优的最优值、平均值、标准差3项指标.由于统计得到的数据量较大,不便于观察,且根据不同测试函数得到的数据具有较大的数量级差异,将依次根据式(8)~(12) 对统计结果进行综合评价.
1) 为防止较大的数量级差异导致汇总时较大数据将较小数据掩盖,且为了将正向与反向评价指标统一规范,对各评价指标按下式标准化处理.
正向指标规范化:
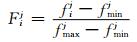 (8)
(8)
反向指标规范化:
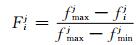 (9)
(9)
式中:fij表示相应参数在第i种取值情况下第j项(j=1, 2, 3分别代表最优值、平均值、标准差)指标对应测试值;fminj表示相应参数第j项指标对应测试值的最小值;fmaxj表示相应参数第j项指标对应测试值的最大值;Fij表示各测试值对应的标准化处理值.
2) 针对不同测试函数所得3项指标的各组标准值进行加权平均.
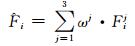 (10)
(10)
式中: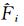
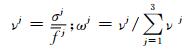 (11)
(11)
其中:σj表示所测试参数第j项指标标准值的标准差;fj表示所测试参数第j项指标标准值的平均值;νj表示所测试参数第j项指标标准值的变异系数.
3) 将上述针对4项测试函数各自所求得的标准值求取平均值作为综合评价指标.
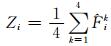 (12)
(12)
式中:Zi表示相应参数在第i种取值情况下的综合评价值;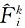
| step a | step b | θ | step cmax | step cmin | |||||
| 参数取值 | 评价值 | 参数取值 | 评价值 | 参数取值 | 评价值 | 参数取值 | 评价值 | 参数取值 | 评价值 |
| 0.1 | 0.794 9 | 0.1 | 0.487 9 | 0.1 | 0.805 0 | 0.1 | 0.645 5 | 100 | 0.438 2 |
| 0.3 | 0.902 5 | 0.3 | 0.542 9 | 0.2 | 0.777 0 | 0.3 | 0.769 7 | 500 | 0.483 1 |
| 0.5 | 0.925 4 | 0.5 | 0.655 2 | 0.3 | 0.757 7 | 0.5 | 0.781 3 | 1 000 | 0.504 0 |
| 0.7 | 0.922 2 | 0.7 | 0.734 5 | 0.4 | 0.705 7 | 0.7 | 0.723 3 | 5 000 | 0.568 7 |
| 0.9 | 0.914 3 | 0.9 | 0.765 2 | 0.5 | 0.617 7 | 0.9 | 0.727 2 | 10 000 | 0.737 0 |
| 1.1 | 0.801 7 | 1.1 | 0.822 4 | 0.6 | 0.643 5 | 1.1 | 0.501 3 | 50 000 | 0.746 7 |
| 1.3 | 0.762 5 | 1.3 | 0.997 4 | 0.7 | 0.556 5 | 1.3 | 0.503 3 | 100 000 | 0.711 1 |
| 1.5 | 0.771 7 | 1.5 | 1.000 0 | 0.8 | 0.462 2 | 1.5 | 0.377 5 | 500 000 | 0.661 8 |
| 1.7 | 0.600 6 | 1.7 | 0.980 3 | 0.9 | 0.419 5 | 1.7 | 0.309 9 | 1 000 000 | 0.5467 |
| 1.9 | 0.517 0 | 1.9 | 0.963 1 | 1.9 | 0.053 4 | 5 000 000 | 0.348 7 | ||
| 2.1 | 0.895 2 | ||||||||
| 2.3 | 0.579 5 | ||||||||
| 2.5 | 0.446 1 | ||||||||
| 2.7 | 0.491 0 | ||||||||
由表 3可知,当step a∈[0.3, 0.9],step b∈[1.3, 1.9],θ∈[0.1, 0.4],step cmin∈[0.3, 0.9],step cmax∈[104, 105]时,综合评价指标均稳定在较高取值水平,NWPA算法寻优效果较好,能够发挥出相对稳定的高性能.
3 水库优化调度应用本文以某年调节综合利用水库优化调度问题为实例[14],进一步检验提出的NWPA算法及建议的参数取值范围的有效性.该水库正常蓄水位160 m,死水位136 m,5月初至8月底为汛期,汛限水位155 m;保证出力12.5万kW,装机容量32万kW,综合出力系数8.5.已知年入库径流过程,优化最大年发电量.
目标函数:
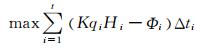 (13)
(13)
式中:K为综合出力系数;qi为第i时段发电流量;Hi为第i时段平均水头;Δti为第i时段的长;t=12,为时段数;Φi表示第i时段包括发电流量、出力等在内的约束条件对应的综合罚函数,当约束条件全部满足时Φi=0,否则Φi>0.
流量约束罚函数:
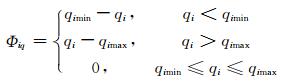 (14)
(14)
出力约束罚函数:
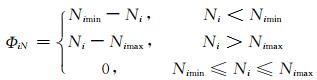 (15)
(15)
式中:qimin、qimax分别表示第i时段要求的最小发电流量与最大允许发电流量;Φiq表示第i时段发电流量约束对应罚函数;Nimin、Nimax分别表示第i时段的最小与最小允许出力;ΦiN表示第i时段出力约束对应罚函数.
综合罚函数为
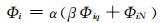 (16)
(16)
式中:Φi表示第i时段对应综合罚函数;α为罚系数(取α=20);β为平衡不同惩罚项量级系数(取β=0.1).
将各时段末的水库蓄水位Z=(z1, z2, …, zT)选取为T维决策空间中个体狼所处位置,对NWPA算法展开寻优实验,并与WPA算法、PSO算法、动态规划(DP)对比.实验中,NWPA、WPA、PSO 3种算法取经验值(同前文),群体数量统一选取为100,最大迭代次数均选取为800次;对于NWPA算法、WPA算法,L=5,h=4,step a=1.5,hmax=15,step b=0.9,θ=0.2,step cmax=100 000,step cmin=0.5,m=5;对于PSO算法,c1=2,c2=2,ωmax=1.4,ωmin=0.4;对于DP,分别对水位可行域离散100点、1 000点,结果见表 4及图 2.
| 算法 | 总发电量/(亿kW·h) | 标准差 | |
| 最优值 | 平均值 | ||
| DP(离散100点) | 18.357 23 | ||
| DP(离散1000点) | 18.362 64 | ||
| PSO | 18.339 14 | 18.306 11 | 0.049 49 |
| WPA | 18.364 72 | 18.358 18 | 0.005 09 |
| NWPA | 18.365 11 | 18.365 08 | 2.34×10-5 |
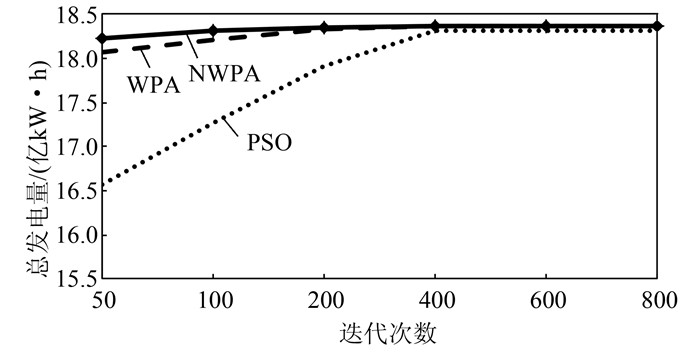
|
| 图 2 收敛曲线对比图 Figure 2 Comparison of convergence curves |
由表 4及图 2可知:1) DP的计算精度依赖于决策变量空间离散的精细程度,离散点越多,计算精度越高,同时占用的计算机内存资源越多,随着优化调度水库的数目增加将会出现维数灾;2) NWPA算法随机搜索的最优值和平均值搜索精度优于DP,但NWPA算法属于随机搜索算法,其稳定性不如DP,也有可能出现搜索精度低于DP的情形;3) 和PSO算法相比,NWPA算法和WPA算法的搜索精度及效率均表现出明显的优势;NWPA算法同WPA算法相比优化效果有明显提升,标准差充分接近0.
表 2和图 2表示的计算结果是在经验参数下取得的.进一步对参数进行摄动分析,并依次根据式(8)~(12) 对统计结果进行综合评价,结果见表 5.
| step a | step b | θ | step cmax | step cmin | |||||
| 参数取值 | 评价值 | 参数取值 | 评价值 | 参数取值 | 评价值 | 参数取值 | 评价值 | 参数取值 | 评价值 |
| 0.1 | 0.592 8 | 0.1 | 0.208 3 | 0.1 | 0.872 5 | 0.1 | 0.541 7 | 100 | 0.631 7 |
| 0.3 | 0.935 6 | 0.3 | 0.569 4 | 0.2 | 0.863 0 | 0.3 | 0.811 4 | 500 | 0.766 1 |
| 0.5 | 0.942 0 | 0.5 | 0.734 1 | 0.3 | 0.847 6 | 0.5 | 0.879 9 | 1 000 | 0.730 7 |
| 0.7 | 0.982 2 | 0.7 | 0.880 9 | 0.4 | 0.814 2 | 0.7 | 0.856 8 | 5 000 | 0.887 8 |
| 0.9 | 0.928 0 | 0.9 | 0.889 9 | 0.5 | 0.621 6 | 0.9 | 0.809 7 | 10 000 | 0.917 0 |
| 1.1 | 0.884 8 | 1.1 | 0.899 9 | 0.6 | 0.530 2 | 1.1 | 0.627 6 | 50 000 | 0.931 7 |
| 1.3 | 0.884 4 | 1.3 | 0.999 4 | 0.7 | 0.527 4 | 1.3 | 0.322 3 | 100 000 | 0.901 7 |
| 1.5 | 0.872 1 | 1.5 | 0.995 2 | 0.8 | 0.602 9 | 1.5 | 0.418 6 | 500 000 | 0.590 8 |
| 1.7 | 0.525 4 | 1.7 | 0.989 9 | 0.9 | 0.464 2 | 1.7 | 0.416 9 | 1 000 000 | 0.512 5 |
| 1.9 | 0.487 1 | 1.9 | 0.963 6 | 1.9 | 0.339 2 | 5 000 000 | 0.499 9 | ||
| 2.1 | 0.890 5 | ||||||||
| 2.3 | 0.599 6 | ||||||||
| 2.5 | 0.807 1 | ||||||||
| 2.7 | 0.350 4 | ||||||||
由表 5可知,上述5个参数取值范围为step a∈[0.3, 0.9],step b∈[1.3, 1.9],θ∈[0.1, 0.4],step cmin∈[0.3, 0.9],step cmax∈[104, 105],与基准测试函数实验结果相同,即上述建议的参数取值范围对基准测试函数和水库优化调度均是有效的.进一步,针对上述水库优化调度案例,通过参数组合-寻优实验,将NWPA算法的上述5个参数在建议的取值范围内进行最佳组合,即为step a=0.5,step b=1.5,θ=0.2,step cmax=105,step cmin=0.3;相应的水库优化调度求解结果为:最优值18.365 13亿kW·h,平均值18.365 13亿kW·h,标准差6.17×10-7.对比表 4数据可知,NWPA参数优化组合后,标准差有明显的减少,算法性能得到进一步提升.
4 结语本文针对WPA算法在实际应用中存在着过分强调个体的独立性、缺乏群体之间信息的共享及个体对历史经验的认知学习等问题进行了改进,提出了新的狼群算法NWPA,并进行了基准测试函数NWPA寻优和水库优化调度应用研究.
1) NWPA算法的寻优能力及收敛速度优于PSO算法、WPA算法.
2) NWPA算法的5个重要参数的有效取值范围为:step a∈[0.3, 0.9],step b∈[1.3, 1.9],θ∈[0.1, 0.4],step cmin∈[0.3, 0.9],step cmax∈[104, 105].
3) 对于水库优化调度问题,NWPA算法的5个重要参数建议取值为:step a=0.5,step b=1.5,θ=0.2,step cmax=105,step cmin=0.3.
4) NWPA算法属于随机搜索算法,其稳定性不如DP;从本文的算例可知,NWPA算法随机搜索的最优值和平均值搜索精度优于DP,但也有可能出现搜索精度低于DP的情形.
本文关于NWPA算法的结论是在对几个基准测试函数寻优和水库优化调度求解仿真实验的基础上得到的,NWPA算法在水资源系统优化规划和管理中的应用还需进一步研究.
| [1] |
钟登华, 熊开智, 成立芹. 遗传算法的改进及其在水库优化调度中的应用研究[J].
中国工程科学, 2003, 5(9): 22–26.
Zhong Denghua, Xiong Kaizhi, Cheng Liqin. The improvement of genetic algorithm and its application to the optimal operation of reservoirs[J]. Engineering Science, 2003, 5(9): 22–26. |
| [2] |
和吉, 胡西林, 邱林, 等. 粒子群优化算法在水库调度中的应用[J].
中州大学学报, 2007, 24(1): 110–122.
He Ji, Hu Xilin, Qiu Lin, et al. Application of particle swarm optimization to reservoir regulation[J]. Journal of Zhongzhou University, 2007, 24(1): 110–122. |
| [3] |
段海滨, 王道波, 朱家强, 等. 蚁群算法理论及应用研究的进展[J].
控制与决策, 2004, 19(12): 1321–1340.
Duan Haibin, Wang Daobo, Zhu Jiaqiang, et al. Development on ant colony algorithm theory and its application[J]. Control and Decision, 2004, 19(12): 1321–1340. DOI:10.3321/j.issn:1001-0920.2004.12.001 |
| [4] |
秦全德, 程适, 李丽, 等. 人工蜂群算法研究综述[J].
智能系统学报, 2014, 9(2): 127–135.
Qin Quande, Cheng Shi, Li Li, et al. Artificial bee colony algorithm:a survey[J]. CAAI Transactions on Intelligent Systems, 2014, 9(2): 127–135. DOI:10.3969/j.issn.1673-4785.201307019 |
| [5] |
彭勇, 唐国磊, 薛志春. 基于改进人工鱼群算法的梯级水库群优化调度[J].
系统工程理论与实践, 2011, 31(6): 1118–1125.
Peng Yong, Tang Guolei, Xue Zhichun. Optimal operation of cascade reservoirs based on improved artificial fish swarm algorithm[J]. Systems Engineering-Theory & Practice, 2011, 31(6): 1118–1125. DOI:10.12011/1000-6788(2011)6-1118 |
| [6] |
刘长平, 叶春明. 一种新颖的仿生群智能优化算法:萤火虫算法[J].
计算机应用研究, 2011, 28(9): 3295–3297.
Liu Changping, Ye Chunming. Novel bioinspired swarm intelligence optimization algorithm:firefly algorithm[J]. Application Research of Computers, 2011, 28(9): 3295–3297. |
| [7] | Yang Chenguang, Tu Xuyan, Chen Jie. Algorithm of marriage in honey bees optimization based on the wolf pack search[C]// Proceedings of International Conference on Intelligent Pervasive Computing. Jeju island, Korea, Oct.11-13, 2007:462-467. |
| [8] | Liu Changan, Yan Xiaohu, Lin Chunyang, et al. The wolf colony algorithm and its application[J]. Chinese Journal of Electronics, 2011, 20(2): 212–216. |
| [9] |
周强, 周永权. 一种基于领导者策略的狼群搜索算法[J].
计算机应用研究, 2013, 30(9): 2629–2632.
Zhou Qiang, Zhou Yongquan. Wolf colony search algorithm based on leader strategy[J]. Application Research of Computers, 2013, 30(9): 2629–2632. |
| [10] |
吴虎胜, 张凤鸣, 吴庐山. 一种新的群体智能算法--狼群算法[J].
系统工程与电子技术, 2013, 35(11): 2430–2438.
Wu Husheng, Zhang Fengming, Wu Lushan. A new swarm intelligence algorithm-wolf pack algorithm[J]. Systems Engineering and Electronics, 2013, 35(11): 2430–2438. |
| [11] | Li Chenming, Du Yichun, Wu Jianxing, et al. Synchronizing chaotification with support vector machine and wolf pack search algorithm for estimation of peripheral vascular occlusion in diabetes mellitus[J]. Biomedical Signal Processing and Control, 2014, 9: 45–55. DOI:10.1016/j.bspc.2013.10.001 |
| [12] |
伊廷华, 王传伟, 李宏男. 基于等级划分狼群算法的三维传感器优化布置方法研究[J].
建筑结构学报, 2014, 35(4): 223–229.
Yi Tinghua, Wang Chuanwei, Li Hongnan. Hierarchic wolf algroithm for optimal triaxial sensor placement[J]. Journal of Building Structures, 2014, 35(4): 223–229. |
| [13] |
伊廷华, 王传伟, 李宏男. 利用分布式狼群算法进行三维传感器优化布置的方法研究[J].
振动工程学报, 2014, 27(5): 669–675.
Yi Tinghua, Wang Chuanwei, Li Hongnan. Optimal triaxial sensor placement using distributed wolf algroithm[J]. Journal of Vibration Engineering, 2014, 27(5): 669–675. |
| [14] |
王建群, 贾洋洋, 肖庆元. 狼群算法在水电站水库优化调度中的应用[J].
水利水电科技进展, 2015, 35(3): 1–4.
Wang Jianqun, Jia Yangyang, Xiao Qingyuan. Application of wolf pack search algorithm to optimal operation of hydropower station[J]. Advances in Science and Technology of Water Resources, 2015, 35(3): 1–4. DOI:10.3880/j.issn.1006-7647.2015.03.001 |
| [15] |
黄少荣. 粒子群优化算法综述[J].
计算机工程与设计, 2009, 30(8): 1977–1980.
Huang Shaorong. Survey of particle swarm optimization algorithm[J]. Computer Engineering and Design, 2009, 30(8): 1977–1980. |
| [16] | Neculai Andrei. An unconstrained optimization test functions collection[J]. Advanced Modeling and Optimization, 2008, 10(1): 147–161. |
| [17] |
张超, 李哲敏, 董晓霞, 等. 金砖国家农业发展水平分析--基于熵权法和变异系数法的比较研究[J].
科技与经济, 2014, 27(162): 42–46.
Zhang Chao, Li Zhemin, Dong Xiaoxia, et al. Analysis of agricultural development level of brics-comparative study based on entropy weight method and variation coefficient method[J]. Science & Technology and Economy, 2014, 27(162): 42–46. |
 2017, Vol. 50
2017, Vol. 50



