文章信息
- 程文锋, 文武
- CHEN Wenfeng, WEN Wu
- 变压器铁芯等效磁导率的反演计算方法
- Equivalent magnetic permeability inversion calculation method of transformer core
- 武汉大学学报(工学版), 2018, 51(11): 975-979
- Engineering Journal of Wuhan University, 2018, 51(11): 975-979
- http://dx.doi.org/10.14188/j.1671-8844.2018-11-006
-
文章历史
- 收稿日期: 2017-11-23
2. 武汉力中电气科技有限公司,湖北 武汉 430072;
3. 武汉大学电气工程学院,湖北 武汉 430072
2. Wuhan Lizhong Electric Technology Co., Ltd., Wuhan 430072, China;
3. School of Electrical Engineering, Wuhan University, Wuhan 430072, China
有限元数值计算方法在变压器等高压电气设备的设计中的广泛应用,对缩短设备的开发周期、提高高压电气产品的质量起到了巨大的推动作用.材料参数的准确性是提高数值计算精度的前提条件.为减小铁芯的涡流损耗,变压器的铁芯通常采用硅钢片叠制而成,硅钢片的厚度一般小于1 mm,其表面涂有一层厚度小于0.025 mm的绝缘膜.在采用有限元方法分析实际变压器电磁问题时,如果将铁芯计算模型精细到片状结构,将产生海量计算数据,即使在计算机软、硬件技术得到高度发展的今天,也难以满足计算要求.在实际计算中,为减小计算量,通常忽略铁芯的片状结构,而将铁芯视为由均匀材料构成的整体[1-2].因此,铁芯的磁导率也应该采用等效磁导率.但在实际应用中铁芯的磁导率往往采用厂家提供的数据,而这些数据是通过单片或几片硅钢片采用试验方法测出的[3-5],它与将铁芯视为均匀材料时的等效磁导率存在一定的差异.因此,如何得到将铁芯视为整体结构时的等效参数(磁导率)是制约数值计算精度的主要因素之一.
智能反演计算为复杂模型等效参数提供了一种有效计算方法[6],该方法已在岩土工程[7-10]、地球物理[11-13]、遥感遥测[13-15]等领域等到广泛应用.
本文拟探索采用遗传智能计算技术,通过硅钢片的磁导率,反演计算出铁芯整体等效磁导率.
1 计算原理智能反演计算方法是智能算法、非线性科学、系统科学、不确定性科学等交叉融合发展起来的新型边缘分支学科,反演计算也称为反问题求解.
一般电磁学问题均可表示成如下偏微分方程形式边值问题:
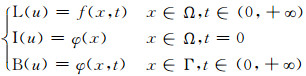 (1)
(1)
式中:u=u(x, t), 为微分方程的解; f(x, t)为源项; φ(x)、φ(x, t)分别为初始值、边界值;L、I、B分别为微分方程算子、初始条件算子、边界条件算子;Ω为求解区域, Γ是其边界.
当u=u(x, t)为待求量, 其余的都为己知量时,构成电磁学正问题.若u=u(x, t)可实测部分或全部值, 而算子L中某些参数未知,则构成参数反演问题.
变压器铁芯材料参数反演的基本思想是忽略铁芯的叠片结构,将铁芯视为均匀材料的整体,计算铁芯周围磁场分布为正问题;在已知铁芯周围实际磁场测量值的条件下,采用遗传等优化算法不断调整仿真模型中材料等效磁导率,使空间磁场的测量值与仿真值一致,此时仿真模型中的材料的磁导率可视为铁芯仿真计算时的等效磁导率.
本文计算原理如图 1所示.图中ψ(u)为适应度函数,ε为收敛精度.

|
| 图 1 铁芯磁导率反演计算原理图 Fig. 1 Principle of inversion calculation for core magnetic permeability |
适应度函数,也称为目标函数,是遗传算法中衡量个体优劣程度的函数,它决定个体繁殖的数量或是否消亡.在参数反演计算中,假定在磁场分布的空间取M个测量点,定义适应度函数为归一化后的各个测量点的仿真值与试验值的误差的最小二乘方程:
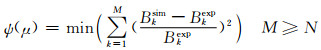 (2)
(2)
其中:μ为铁芯磁导率; M为采样点个数; N为待求材料参数的数量;Bksim为有限元仿真的磁感应强度值; Bkexp为试验测试的磁感应强度值.
2 计算模型从计算原理看,测量点空间磁感应强度的试验值应通过实际装置的测量来得到,由于实际变压器铁芯周围的磁感应强度测量较为困难,本文将分别建立几何尺寸相等的2套铁芯缩比模型,即精细化模型和简化模型.其中精细化模型同时考虑铁芯的叠片结构及硅钢片之间的绝缘层,并将精细化模型的计算结果作为测量值;简化模型忽略铁芯叠片结构,将铁芯视为均匀材料的整体,简化模型为参数优化提供仿真数据.
铁芯缩比计算模型如图 2所示.其中,铁芯直径为20 mm,高度为80 mm;线圈内半径为11 mm,厚度为1 mm.

|
| 图 2 铁芯及励磁线圈模型 Fig. 2 Calculation node of transformer core and coils |
精细模型与简化模型的外形尺寸相同,其区别主要在铁芯结构.图 3为精细模型与简化模型线圈中央的截面图.图 3(a)为精细模型截面,其中硅钢片厚0.8 mm,硅钢片间绝缘膜厚度0.05 mm,硅钢片相对磁导率为5 000;图 3(b)为铁芯简化模型截面,铁芯为均匀材料的整体结构,其磁导率即为待反演计算值.

|
| 图 3 铁芯截面图 Fig. 3 Cross-sections of transformer core |
根据模型的对称性,取1/8模型进行计算,如图 4所示,图中,在铁轭中间沿半径为15 mm的圆弧上取20个等间距采样点.

|
| 图 4 1/8计算模型 Fig. 4 1/8 calculation model |
设硅钢片为无取向钢,相对磁导率为5 000,励磁电流密度为500 kA/m2,分别按精细模型和磁导率为5 000的简化模型计算磁场分布,图 5为铁芯及线圈的磁感应强度分布云图.

|
| 图 5 铁芯磁感应强度分布图(单位:T) Fig. 5 Magnetic flux density of core and coil (unit:T) |
2种计算模型采样点的磁感应强度如图 6所示.

|
| 图 6 采用点磁感应强度 Fig. 6 Graph of magnetic flux density at sampling points |
由图 6的计算结果可以看出,过铁芯柱中心与硅钢片平面对应位置磁感应强度值较为一致,但与叠片平面垂直方向2种模型的计算值存在较大的差异.因而,将铁芯视为均匀材料的整体,且用硅钢片的磁导率作为铁芯的等效磁导率时,给数值计算结果带来一定的误差.为提高数值仿真的计算精度,有必要探索铁芯整体等效磁导率的等值方法.
3.2 铁芯等效磁导率反演计算由于硅钢片之间存在绝缘涂膜,且硅钢片之间并非理想接触,即使单片硅钢片是各向同性,叠装成铁芯后沿不同方向的磁导率也不可能相同,因此,设铁芯的等效磁导率为各向异性.
在采用遗传算法进行反演计算时,设铁芯等效相对磁导率的取值范围为
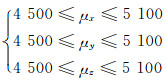 (3)
(3)
种群的大小为20,最大遗传代数为40,个体长度为20,代沟为0.95,交叉概率为0.7,变异概率为0.01.借助Matlab遗传算法工具箱和电磁场计算软件Ansys联合仿真,按图 1所示的流程,反演计算铁芯的等效磁导率.等效磁导率最优解进化过程如图 7所示.

|
| 图 7 最优解进化过程 Fig. 7 Evolutionary process of optimizing solution |
由图 7可以看出,当进化到第35代时基本收敛,输出铁芯等效磁导率最优解为
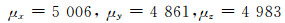 (4)
(4)
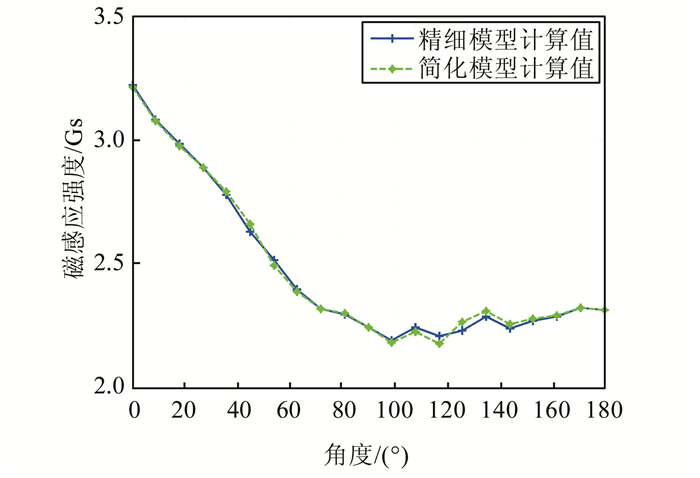
以式(4)值作为铁芯简化模型的等效磁导率计算铁芯周围的磁场分布,采样点在精细模型和简化模型下的磁感应强度计算结果如图 8所示,计算结果表明2种模型的计算结果具有很好的一致性.
|
| 图 8 最优等效磁时采用点磁感应强度对比 Fig. 8 Graph of magnetic flux density at sampling points using equivalent parameter |
由以上计算结果可知,当忽略铁芯的叠片结构,将铁芯视为同种材料的整体时,即使硅钢片磁导率是各向同性的非取向钢,铁芯沿不同方向的等效磁导率也应存在差异,其中在与硅钢片平行方向等效磁导率与硅钢片磁导率基本相等,但在与硅钢片平面垂直的方向,等效磁导率较硅钢片磁导率大约减小2.8%.
4 结论本文采用智能遗传算法,对叠片结构的变压器铁芯等效磁导率参数反演计算方法进行了研究,得到如下结论:
1) 采用智能遗传算法反演计算铁芯等效磁导率的方法是可行的.
2) 在变压器电磁问题的有限元计算中,铁芯采用单片硅片的磁导率参数会带来一定的误差.
3) 即使硅钢片为非取性的各向同性材料,取铁芯平行于硅钢片方向的等效磁导率等于硅钢片磁导率,与硅钢片垂直方向的等效磁导率略小于硅钢片磁导率,可有效提高有限元法计算的精度.
| [1] |
肖华, 吴广宁, 蒋伟, 等. 基于有限元法的单相变压器直流偏磁仿真研究[J]. 高压电器, 2010, 46(9): 39-47. Xiao Hua, Wu Guangning, Jiang Wei, et al. Simulation of DC bias of single-phase transformer based on FEM[J]. High Voltage Apparatus, 2010, 46(9): 39-47. |
| [2] |
王楠, 刘宝成, 臧春艳, 等. 基于磁-结构耦合场的变压器绕组形变分析[J]. 高压电器, 2016, 52(1): 94-100. Wang Nan, Liu Baocheng, Zang Chunyan, et al. Analysis of transformer winding deformation based on magnetics-structure coupled-field[J]. High Voltage Apparatus, 2016, 52(1): 94-100. |
| [3] |
GB/T 3655-2008用爱泼斯坦方圈测量电工钢片(带)磁性能的方法[S]. GB/T 3655-2008 Methods of Measurement of the Magnetic Properties of Electrical Steel Sheet and Strip by Means of an Epstein Frame[S]. |
| [4] |
韩赞东, 李晓阳. 基于动态磁化的结构钢磁导率和电磁损耗测量方法[J]. 清华大学学报(自然科学版), 2014, 54(11): 1471-1474. Han Zandong, Li Xiaoyang. Measurement of magnetic permeability and magnetic loss of structural steel for dynamic magnetization[J]. Journal of Tsinghua University (Natural Science Edition), 2014, 54(11): 1471-1474. |
| [5] |
白旭东, 刘巧风, 王飞, 等. 铁磁材料磁导率测量实验研究[J]. 大学物理试验, 2009, 22(3): 5-7. Bai Xudong, Liu Qiaofeng, Wang Fei, et al. Study on magnetic permeability measurement experiment of ferromagnetic materials[J]. Physical Experiment of College, 2009, 22(3): 5-7. |
| [6] |
李守巨, 刘迎曦, 孙伟. 智能计算与参数反演[M]. 北京: 科学出版社, 2008: 1-37. Li Shouju, Liu Yinxi, Sun Wei. Intelligent Calculation and Parameter Inversion[M]. Beijing: Science Press, 2008: 1-37. |
| [7] |
周济芳, 李建林, 刘杰. 隔河岩水电站边坡岩体宏观力学参数的有限元反演分析[J]. 岩石力学与工程学报, 2004, 23(1): 4506-4508. Zhou Jifang, Li Jianlin, Liu Jie. Back analysis of macromechanics parameters of rock masses of the slope of Geheyan Hydraulic Power Station[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(1): 4506-4508. |
| [8] |
尚守平, 雷敏, 奉杰超. 砌体结构分离式有限元模型的参数反演[J]. 广西大学学报(自然科学版), 2013, 38(1): 1-8. Shang Shouping, Lei Min, Feng Jiechao. Parameter inversion of micro-model of masonry structure[J]. Journal of Guangxi University (Natural Science Edition), 2013, 38(1): 1-8. DOI:10.3969/j.issn.1001-7445.2013.01.001 |
| [9] |
杜万军. 有限元在岩体渗透参数反演中的应用[J]. 山西建筑, 2017, 43(12): 70-72. Du Wanjun. Application of finite element method in rock mass seepage parameter inversion[J]. Shanxi Architecture, 2017, 43(12): 70-72. DOI:10.3969/j.issn.1009-6825.2017.12.037 |
| [10] |
陈怀震, 印兴耀, 张金强, 等. 基于方位各向异性弹性阻抗的裂缝岩石物理参数反演方法研究[J]. 地球物理学报, 2014, 57(10): 3431-3441. Chen Huaizhen, Yin Xingyao, Zhang Jinqiang, et al. Seismic inversion for fracture rock physics parameters using azimuthally anisotropic elastic impedance[J]. Chinese Journal of Geophysics, 2014, 57(10): 3431-3441. DOI:10.6038/cjg20141029 |
| [11] |
刘云华, 汪驰升, 单新建, 等. 芦山Ms7.0级InSAR地震形变观测及震源参数反演[J]. 地球物理学报, 2014, 57(8): 2495-2506. Liu Yunhua, Wang Chisheng, Shan Xinjian, et al. Result of SAR differential interferometry for the co-seismic deformation and source parameter of the Ms7.0 Lushan Earthquake[J]. Chinese Journal of Geophysics, 2014, 57(8): 2495-2506. |
| [12] |
桂金咏, 高建虎, 雍学善, 等. 基于双相介质理论的储层参数反演方法[J]. 地球物理学报, 2015, 58(9): 3424-3438. Gui Jinyong, Gao Jianhu, Yong Xueshan, et al. Inversion of reservoir parameters based on dual-phase media theory[J]. Chinese Journal of Geophysics, 2015, 58(9): 3424-3438. |
| [13] |
李文娟, 赵传燕, 别强, 等. 基于机载激光雷达数据的森林结构参数反演[J]. 遥感技术与应用, 2015, 30(5): 917-924. Li Wenjuan, Zhao Chuanyan, Bie Qiang, et al. Retrieval of the forest structural parameters using airborne LiDAR data[J]. Remote Sensing Technology and Application, 2015, 30(5): 917-924. |
| [14] |
吴志义, 李佳玉. 各向异性介质辐射特性参数联合反演[J]. 光散射学报, 2017, 29(3): 203-209. Wu Zhiyi, Li Jiayu. Joint inversion of radiative properties of anisortropic medium[J]. The Journal of Light Scattering, 2017, 29(3): 203-209. |
| [15] |
李喆, 郭旭东, 古春, 等. 高光谱吸收特征参数反演草地光合有效辐射吸收率[J]. 遥感学报, 2016, 20(2): 290-302. Li Zhe, Guo Xudong, Gu Chun, et al. Spectral absorption characteristic parameters in inversing FAPAR of natural grassland[J]. Journal of Remote Sensing, 2016, 20(2): 290-302. |
 2018, Vol. 51
2018, Vol. 51




