文章信息
- 郭怿品, 李典庆, 唐小松, 曹子君
- GUO Yipin, LI Dianqing, TANG Xiaosong, CAO Zijun
- 基于Bootstrap方法的堆石坝坝坡稳定可靠度分析
- Slope stability reliability of rockfill dams based on Bootstrap method
- 武汉大学学报(工学版), 2019, 52(2): 106-115
- Engineering Journal of Wuhan University, 2019, 52(2): 106-115
- http://dx.doi.org/10.14188/j.1671-8844.2019-02-002
-
文章历史
- 收稿日期: 2018-01-10
心墙堆石坝是水利水电工程中最常见的坝型之一,它可以充分利用当地的天然材料,适应不同的地质条件,施工方法简便且抗震性能好.近年来,这种坝型在国内许多工程中慢慢推广开来,如西南地区的糯扎渡水电站、两河口水电站、双江口水电站等.我国西南地区地形地质条件复杂,地震频发,所以在西南流域心墙堆石坝的设计中,地震是非常重要的一个考虑因素.如何准确地对心墙堆石坝进行坝坡稳定分析是坝体设计中关注的一个重要方面.为此,我国的2套土石坝设计规范[1, 2]均对此作出了详细说明和要求.
由于心墙堆石坝的主要筑坝材料是心墙料和堆石料,所以在堆石坝坝坡稳定分析中,心墙料和堆石料的抗剪强度参数对堆石坝的稳定起到了决定性作用.虽然筑坝材料经过人工处理,与天然岩土材料相比更为均匀且抗剪强度参数的变异性较小,但室内三轴压缩试验表明,心墙料和堆石料的抗剪强度参数仍然表现出不可忽略的变异性.在用传统的安全系数法分析堆石坝的坝坡稳定时,抗剪强度参数往往被视为确定值,这样的分析方法忽略了抗剪强度参数的变异性,一定程度上无法真实地反映坝体的实际安全状况.与安全系数法相比,可靠度方法可以将抗剪强度参数的变异性纳入到堆石坝的坝坡稳定分析当中,为堆石坝的坝坡稳定分析提供了一条有效途径[3, 4].
抗剪强度参数变异性的存在导致了在坝坡稳定可靠度分析中的各种不确定性,包括参数本身固有的不确定性、计算方法假定引起的模型不确定性以及试验数据有限带来的统计不确定性[5].在以往用可靠度方法评估坝坡稳定情况过程中,筑坝材料抗剪强度参数被视为随机变量,根据试验数据的均值和标准差获得分布参数,而采用AIC准则一类的信息准则来识别参数的分布类型.这种方法将参数本身固有的不确定性和计算方法中假定引起的模型不确定性纳入了可靠度分析当中.当试验数据的样本容量很大时,样本均值和样本标准差确定的分布参数以及AIC准则识别的分布类型是相对准确的,然而由于试验数据有限,过少的数据无法真实地描述参数的概率分布情况,导致计算得到的样本均值、标准差和AIC值具有较大的变异性[6],这种变异性直接导致了分布参数与分布类型存在明显的统计不确定性.
为了计算简便,早期研究将心墙料和堆石料的抗剪强度参数视为独立变量,只需建立抗剪强度参数的概率分布函数即可.近年的研究表明,心墙料和堆石料的抗剪强度参数具有一定的相关性,且这种相关性对坝坡稳定可靠度有着显著的影响.研究发现,采用摩尔-库伦准则表征的心墙料的抗剪强度参数(即粘聚力c和内摩擦角φ)具有负相关性,而利用邓肯非线性强度准则表征的堆石料的抗剪强度参数(即φ0和Δφ)具有正相关性[7, 8],这些相关性都能明显影响坝坡的稳定可靠度.Copula理论是一种可以任意构建相关参数联合概率分布函数的方法,该方法可以描述多种类型的相关结构.文献[9]提出了一种基于Copula函数的边坡可靠度分析方法.在用Copula方法表征抗剪强度参数相关性的过程中,相关结构的确定(Copula函数的选择)也可以通过AIC准则之类的信息准则进行.与参数边缘分布确定相同,受样本数目的限制,在建立联合概率分布函数时,参数间的相关系数和相关结构也会存在明显的统计不确定性.
因此,在抗剪强度参数的联合概率分布函数构建过程中,共包含边缘分布参数、边缘分布类型、相关系数和相关结构4种统计不确定性.
Bootstrap方法可以对原始试验数据进行有放回随机抽样获得大量与原始数据相同样本容量的子样本,然后基于Bootstrap子样本计算统计量的估计值,最终获得统计量的抽样分布.近年来,越来越多的学者将Bootstrap方法引入岩土工程领域,文献[10]用Bootstrap方法研究了土体参数样本均值和标准差的变异性对支护开挖失效概率的影响,文献[6]用Bootstrap方法研究了土体参数统计不确定性对边坡可靠度计算结果的影响.
在以往的可靠度分析中,由于样本量的限制,参数的边缘分布函数或参数的联合概率分布函数是根据原始数据和一些假定唯一确定的,由此得到的坝坡失效概率是唯一值,从统计学的角度来看,该方法对坝坡失效概率的度量是一种点估计方法.由于Bootstrap方法可以获得大量与原始样本相同容量的子样本,通过子样本即可获得不同的边缘分布函数,并且可以找到不同的Copula函数来表征每组子样本参数间的相关性,以此获得不同的失效概率值,从而用一个失效概率区间来描述坝坡失效概率的分布情况,使坝坡失效情况的度量从点估计变为了区间估计.
1 堆石坝坝坡稳定可靠度分析方法 1.1 堆石坝坝坡稳定分析计算模型本文采用的算例是我国澜沧江流域的糯扎渡水电站,电站枢纽的主坝是心墙堆石坝.水库正常蓄水位812 m,心墙堆石坝最大坝高261.5 m,总库容237.03亿m3.大坝主要由心墙料、反滤层Ⅰ、反滤层Ⅱ、过渡层、堆石料Ⅰ和堆石料Ⅱ填筑而成.由于反滤层和过渡层占坝体材料比例较小,对坝坡稳定不起决定性作用,所以在可靠度分析中,反滤层和过渡层材料抗剪强度参数被视为确定性变量,心墙料和堆石料抗剪强度参数被视为随机变量.表 1给出了坝体材料的参数.本文的计算工况为正常运用条件下遇地震的下游坝坡稳定.
| 材料 | 强度参数 | 均值 | 标准差 | 皮尔逊相关系数 |
| 堆石料Ⅰ | φ0/(°) | 53.5 | 2.6 | 0.57 |
| Δφ/(°) | 9.2 | 1.4 | ||
| 堆石料Ⅱ | φ0/(°) | 51.8 | 3.6 | 0.74 |
| Δφ/(°) | 10.0 | 1.7 | ||
| 心墙料 | φ/(°) | 27.3 | 1.8 | -0.38 |
| c/kPa | 93.4 | 24.8 | ||
| 反滤层Ⅰ | φ0/(°) | 49.9 | ||
| Δφ/(°) | 10.1 | |||
| 反滤层Ⅱ | φ0/(°) | 54.1 | ||
| Δφ/(°) | 11.3 | |||
| 过渡层 | φ0/(°) | 49.1 | ||
| Δφ/(°) | 6.7 |
本文采用规范建议的瑞典圆弧法进行坝坡稳定验算,瑞典圆弧法假定滑动面为圆弧,并将滑体划分为若干的条块,忽略条间力的作用,只考虑力矩平衡,从而得到坝坡的稳定安全系数.根据《碾压式土石坝设计规范》(DL/T 5395-2007)[1]的要求,瑞典圆弧法安全系数计算公式为
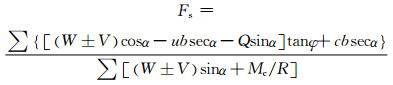 (1)
(1)
式中:W为土条重力;Q和V为地震水平、垂直惯性力;u为作用于土条地面孔隙压力;α为条块重力线与通过此条块底面中点的半径之间的夹角;b为土条宽度;c和φ为土条底面的有效应力抗剪强度指标;Mc为地震水平惯性力对圆心的力矩;R为圆弧半径.
堆石坝的主要填筑材料是心墙料和堆石料,对于心墙料而言,摩尔-库伦准则可以较好地表征其抗剪强度,而对于堆石料而言,由于其颗粒较大,粘聚力可以忽略不计,内摩擦角在低应力条件下较大,而在高应力条件下较小,强度包线呈现非线性特性.因此,《碾压式土石坝设计规范》(DL/T 5395-2007)[1]建议对粗颗粒料采用邓肯非线性强度准则[11]描述其抗剪强度,如图 1所示,表达式为
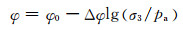 (2)
(2)
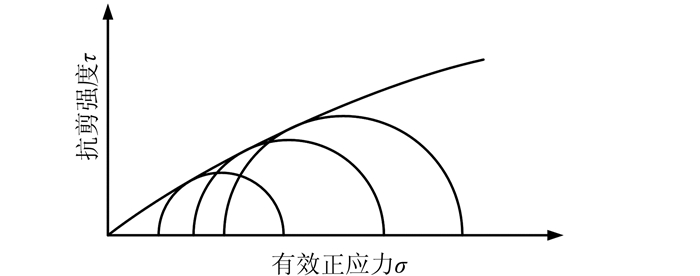
|
| 图 1 非线性强度包线 Fig. 1 Nonlinear strength envelope |
式中:φ为土体的摩擦角;φ0为一个大气压力下的摩擦角;Δφ为σ3增加一个对数周期下φ的减小值;σ3为土体的小主应力;pa为大气压力.
1.2 基于Copula函数的联合分布函数构造方法Copula函数是将变量的联合分布函数与其边缘分布函数联结起来的函数,本质上它也是一种联合分布函数.对于二维情况,Copula函数定义为[0, 1]2空间中边缘分布函数为[0, 1]区间内均匀分布的二维联合分布函数[12]:
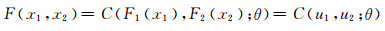 (3)
(3)
式中:F(x1, x2)为变量X1和X2的联合分布函数;u1=F1(x1)和u2=F2(x2)分别为变量X1和X2的边缘分布函数;C(u1, u2; θ)为Copula函数;θ为Copula函数的相关参数.令变量X1和X2的概率密度函数分别为f1(x1)和f2(x2),那么对式(3)两边求导可得变量X1和X2的联合概率密度函数f(x1, x2)为
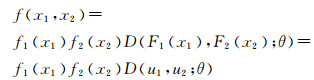 (4)
(4)
式中:D(u1, u2; θ)为Copula函数的密度函数.因此,若已知变量X1和X2的边缘分布函数和Copula函数,利用式(3)和式(4)就可以构造出变量X1和X2的联合分布函数和联合概率密度函数.根据Copula函数的定义,在Copula理论框架下构造变量的联合分布函数可以分为以下2步:1)确定变量的边缘分布函数;2)选择最优的Copula函数表征变量的相关结构.
本文采用AIC(Akaike Information Criterion)准则[13]识别最优的边缘分布函数与最优Copula函数,具有最小AIC值的函数被认为是拟合试验数据概率分布特性最优的函数.在边缘分布识别过程中,AIC值定义为所有试验数据点处概率密度函数值对数和的负2倍与2倍概率分布函数的分布参数数目之和,表达式为
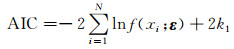 (5)
(5)
式中:f(xi; ε)为备选概率分布函数的密度函数;{xi, i=1, 2, …, N}为试验数据,其中N为样本数目;ε为备选概率分布函数的分布参数向量;k1为备选概率分布函数中分布参数的数目.而在最优Copula函数识别过程中,AIC值定义为所有试验数据点处Copula密度函数值对数和的负2倍与2倍Copula函数的相关参数数目之和,表达式为
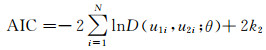 (6)
(6)
式中:k2为Copula函数相关参数的数目,对于二维Copula函数来说k2=1;(u1i, u2i)为试验数据(x1i, x2i)的经验分布值,可由下式计算:
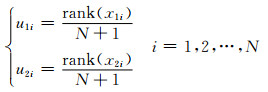 (7)
(7)
式中:rank(x1i)和rank(x2i)分别表示按升序排列时x1i和x2i在整列试验数据x1={x11, x12, …, x1N}和x2={x21, x22, …, x2N}中的秩次.
边缘分布选取工程可靠度分析中常用的正态分布、对数正态分布、极值Ⅰ型分布和威布尔分布作为备选边缘分布函数.正态分布和极值Ⅰ型分布在0处进行左截尾,以满足参数为正值的要求.对于心墙料而言,抗剪强度参数c和φ呈负相关关系,故选取Gaussian、Plackett、Frank以及No.16 Copula函数作为备选Copula函数,这几种Copula函数均能较好地模拟相关系数在(-1, 0)区间内的相关性.而对于堆石料而言,抗剪强度参数φ和Δφ呈正相关关系,故选取Gaussian、Plackett、Frank、Clayton以及Gumbel Copula函数作为备选Copula函数,这几种Copula函数均能较好地模拟相关系数在(0, 1)区间内的相关性.
1.3 堆石坝坝坡稳定可靠度分析步骤工程中常用的可靠度分析方法包括FORM、SORM、RSM、MCS等方法,考虑到算例中极限状态方程形式较为复杂,本文采用MCS方法对坝坡的稳定情况进行可靠度分析,具体计算步骤如下:
1) 通过室内三轴压缩试验获取各材料抗剪强度参数试验值;
2) 根据获取的抗剪强度参数识别参数服从的边缘分布函数与描述参数间相关性的最优Copula函数;
3) 依据式(3)和(4)建立变量的联合概率分布函数;
4) 依据得到的联合概率分布函数,用蒙特卡洛模拟方法生成M组抗剪强度参数的随机模拟值;
5) 搜索滑动面,对于给定的滑动面,将M组抗剪强度参数模拟值代入式(1),得到M个Fs,统计其中的失效样本点数目L(即Fs < 1).给定滑动面的失效概率为pf=L/M;
6) 比较各假定滑动面的失效概率,整体坝坡失效概率为各假定滑动面失效概率最大值pfmax,坝坡稳定的可靠度指标为β=-Φ-1(pfmax).
表 2给出了各材料强度参数边缘分布识别的AIC值.由结果可知,堆石料Ⅰ摩擦角φ服从对数正态分布,Δφ服从威布尔分布,其余2种材料的强度参数均服从极值Ⅰ型分布.
| 材料 | 参数 | 正态 | 对数正态 | 极值Ⅰ型 | 威布尔 |
| 心墙料 | φ | 27.10 | 27.00 | 26.65 | 27.71 |
| c | 58.68 | 58.08 | 57.99 | 58.68 | |
| 堆石料Ⅰ | φ0 | 69.32 | 68.99 | 69.22 | 77.50 |
| Δφ | 52.23 | 53.04 | 55.80 | 51.37 | |
| 堆石料Ⅱ | φ0 | 67.81 | 67.06 | 64.64 | 74.15 |
| Δφ | 49.73 | 47.24 | 45.02 | 55.36 |
表 3给出了堆石料和心墙料各自抗剪强度参数的备选Copula函数AIC计算结果.由结果可知,堆石料Ⅰ、堆石料Ⅱ、心墙料抗剪强度参数服从的最优Copula函数分别为Plackett Copula、Gumbel Copula和Gaussian Copula函数.
| 材料 | Gaussian | Plackett | Frank | No.16 | Clayton | Gumbel |
| 心墙料 | 0.412 | 0.907 | 0.585 | 1.641 | - | - |
| 堆石料Ⅰ | -1.509 | -3.831 | -2.495 | - | -3.592 | -1.624 |
| 堆石料Ⅱ | -5.143 | -4.212 | -4.588 | - | -2.590 | -6.869 |
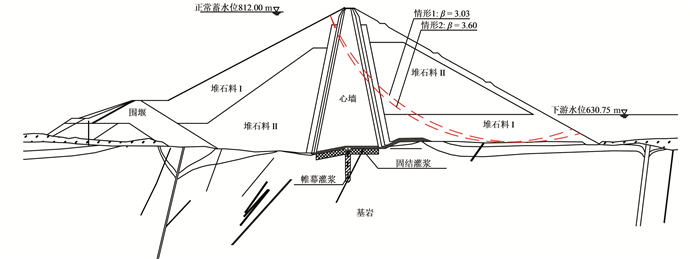
本文的计算工况为非常运用条件Ⅱ的下游坝坡稳定,即正常蓄水位条件下9度地震,考虑垂直地震惯性力向上和向下2种情形.计算结果如表 4所示,最危险滑动面位置如图 2所示.
|
| 图 2 情形1和情形2(正常蓄水位条件下9度地震考虑垂直地震惯性力向上和向下)糯扎渡水电站下游坝坡最危险滑动面 Fig. 2 Critical slip surfaces for downstream slope of Nuozadu dam in condition 1 and condition 2 (normal water level with 9-degree earthquake considering vertical inertia force upward and downward) |
由于堆石坝工程抗剪强度参数的室内三轴试验数据量极少,对于糯扎渡水电站心墙堆石坝而言,心墙料、堆石料Ⅰ、堆石料Ⅱ的试验数据分别只有6组、14组和12组,基于试验数据计算的样本均值和标准差变异性较大,导致了在边缘分布函数和Copula函数识别过程中,获得的AIC值变异性也较大.由此带来了4个方面的统计不确定性:边缘分布参数、边缘分布类型、相关系数和相关结构.本文采用Bootstrap方法度量样本均值、样本标准差和AIC值的变异性.
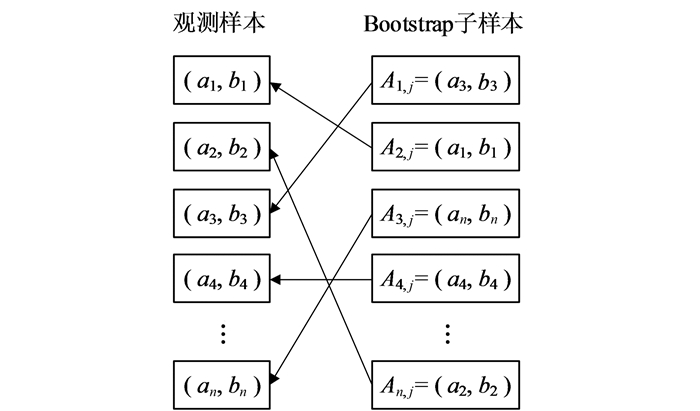
2.1 Bootstrap方法Bootstrap方法可以对原始试验数据进行有放回随机抽样获得大量与原始数据相同样本容量的子样本,然后基于Bootstrap子样本计算统计量的估计值,最终获得统计量的抽样分布.令试验数据为Y={(ai, bi), i=1, 2, …, N},从中有放回地随机抽样N次,可以获得一个与原试验数据相同样本容量的子样本Aj={A1, j, A2, j, …, An, j},该抽样过程如图 3所示.由于该抽样是有放回的随机抽样,所以在Aj中试验数据的某个值可能出现多次也可能不出现.重复上述步骤Ns次,即可获得Ns个Bootstrap子样本.
|
| 图 3 Bootstrap方法抽样原理示意图 Fig. 3 Illustration of the generation of one Bootstrap sample |
Bootstrap方法只依赖原始试验数据,整体抽样过程不包含其他信息与假设.通过每一次抽样,可以获得每一组Bootstrap子样本的样本均值、标准差与识别分布过程中的AIC值.通过多次模拟,即可度量这些值的变异性.该方法的理论依据早已被统计学家所证明[14].而Bootstrap模拟次数取决于目标统计量的收敛情况.一般而言,为达到良好的模拟效果,文献[10]建议Bootstrap模拟土性参数时,模拟次数应达到Ns=10 000.在本算例中,为了使2种计算情形得到的失效概率均值和标准差收敛,模拟次数Ns应达到30 000.
2.2 堆石坝抗剪强度参数统计不确定性模拟根据前述方法可以模拟糯扎渡水电站3种筑坝材料抗剪强度参数均值、标准差以及边缘分布识别过程中获得的AIC值的抽样特性.它们的抽样特性如表 5所示.
| 统计量 | 心墙料 | 堆石料Ⅰ | 堆石料Ⅱ | ||||||||||||||||||||
| c | φ | c | φ | c | φ | ||||||||||||||||||
| Mean | SD | COV | Mean | SD | COV | Mean | SD | COV | Mean | SD | COV | Mean | SD | COV | Mean | SD | COV | ||||||
| 样本均值 | 93.36 | 9.22 | 0.098 | 27.26 | 0.68 | 0.025 | 53.86 | 0.42 | 0.008 | 9.58 | 0.31 | 0.032 | 51.00 | 0.37 | 0.007 | 9.27 | 0.32 | 0.035 | |||||
| 样本标准差 | 21.87 | 5.93 | 0.271 | 1.60 | 0.39 | 0.244 | 0.98 | 0.32 | 0.327 | 0.73 | 0.19 | 0.260 | 0.85 | 0.31 | 0.365 | 0.70 | 0.31 | 0.443 | |||||
| 正态分布的AIC值 | 56.48 | 4.02 | 0.071 | 25.19 | 3.55 | 0.141 | 19.03 | 4.57 | 0.240 | 15.54 | 5.01 | 0.322 | 17.02 | 5.45 | 0.320 | 13.54 | 9.35 | 0.691 | |||||
| 对数正态分布的AIC值 | 56.17 | 3.96 | 0.071 | 25.13 | 3.55 | 0.141 | 19.07 | 4.59 | 0.241 | 15.41 | 5.00 | 0.325 | 16.98 | 5.42 | 0.319 | 13.36 | 9.22 | 0.690 | |||||
| 极值Ⅰ型分布的AIC值 | 56.25 | 4.01 | 0.071 | 25.08 | 3.70 | 0.148 | 20.77 | 5.36 | 0.258 | 15.12 | 5.04 | 0.333 | 16.82 | 4.83 | 0.287 | 13.57 | 8.91 | 0.657 | |||||
| 威布尔分布的AIC值 | 56.60 | 3.94 | 0.070 | 25.81 | 3.65 | 0.141 | 18.51 | 4.31 | 0.233 | 16.36 | 5.09 | 0.311 | 18.40 | 6.45 | 0.351 | 14.51 | 9.79 | 0.675 | |||||
通过30 000次模拟,每一组Bootstrap子样本都可以用AIC准则识别出各种抗剪强度参数服从的最优边缘分布函数,即可通过这种方式比较每种备选概率分布函数被识别为最优边缘分布的次数,从而得到在考虑统计不确定性情况下哪一种备选概率分布函数能更真实地表征该抗剪强度参数的不确定性.表 6给出了不同备选概率分布被识别为最优边缘分布的次数.
| 参数 | 正态 | 对数正态 | 极值Ⅰ型 | 威布尔 | |
| 心墙料 | φ/(°) | 554 | 1 294 | 18 870 | 9 282 |
| c/kPa | 408 | 4 634 | 16 192 | 8 766 | |
| 堆石料Ⅰ | φ/(°) | 951 | 669 | 6 170 | 22 210 |
| Δφ/(°) | 877 | 1 325 | 20 212 | 7 586 | |
| 堆石料Ⅱ | φ/(°) | 564 | 1 082 | 19 847 | 8 507 |
| Δφ/(°) | 62 | 42 | 21 229 | 8 667 | |
从表中的结果可以看出,任何一种备选概率分布函数都不一定能在每一组Bootstrap子样本中被识别为最优边缘分布,但某一种分布可能被识别为最优分布的次数最多,该分布是考虑统计不确定性后拟合参数的最优分布.将表 6结果和表 2比较可以看出,通过原始数据识别出的最优边缘分布与考虑统计不确定性识别出的最优边缘分布不完全相同.对于心墙料和堆石料Ⅱ的抗剪强度参数而言,极值Ⅰ型分布是被识别为最优边缘分布次数最多的分布,这与通过原始数据单次识别的结果是一致的.但是对于堆石料Ⅰ的2种抗剪强度参数φ和Δφ而言,威布尔分布和极值Ⅰ型分布分别通过Bootstrap方法被识别为最优边缘分布的次数最多,φ和Δφ通过原始数据单次识别的最优分布是对数正态分布和威布尔分布.发生这种差异的原因是基于原始数据通过AIC方法识别最优边缘分布的过程中没有考虑AIC值的变异性.从表 6的结果可以看出,这种变异性对识别的准确程度有一定影响.使用Bootstrap方法可以将原始数据的统计不确定性纳入到最优分布的识别中,Bootstrap方法可以通过模拟AIC值的变异性有效地得出不同备选概率分布函数为最优边缘分布的可能性.
同样,在识别最优Copula函数时获得AIC值也可以通过Bootstrap方法获得它的抽样特性.表 7给出了30 000次Bootstrap模拟下识别3种材料各自抗剪强度参数间相关结构的AIC值抽样特性,表 8给出了30 000次模拟下各备选Copula函数被识别为最优相关结构的次数.
| 相关系数与AIC值 | Mean | SD | COV | |
| 心墙料 | 相关系数 | -0.356 | 0.417 | -1.173 |
| Gaussian Copula AIC值 | 24.798 | 105.152 | 4.240 | |
| Plackett Copula AIC值 | 3.046 | 6.756 | 2.218 | |
| Frank Copula AIC值 | 8.410 | 29.398 | 3.496 | |
| No.16 Copula AIC值 | 4.002 | 7.317 | 1.828 | |
| 堆石料Ⅰ | 相关系数 | 0.568 | 0.220 | 0.387 |
| Gaussian Copula AIC值 | -3.943 | 7.070 | -1.793 | |
| Plackett Copula AIC值 | -5.854 | 8.384 | -1.432 | |
| Frank Copula AIC值 | -5.038 | 7.697 | -1.528 | |
| Clayton Copula AIC值 | -5.892 | 9.632 | -1.635 | |
| Gumbel Copula AIC值 | -4.137 | 7.010 | -1.694 | |
| 堆石料Ⅱ | 相关系数 | 0.735 | 1.180 | 0.245 |
| Gaussian Copula AIC值 | -6.918 | 9.315 | -1.346 | |
| Plackett Copula AIC值 | -8.588 | 12.268 | -1.429 | |
| Frank Copula AIC值 | -7.898 | 10.083 | -1.277 | |
| Clayton Copula AIC值 | -1.208 | 13.456 | -11.139 | |
| Gumbel Copula AIC值 | -9.482 | 9.974 | -1.052 | |
| 材料 | Gaussian | Plackett | Frank | No.16 | Clayton | Gumbel |
| 心墙料 | 24 184 | 2 676 | 1 112 | 2 028 | - | - |
| 堆石料Ⅰ | 1 378 | 1 708 | 8 304 | - | 15 986 | 2 624 |
| 堆石料Ⅱ | 624 | 2 981 | 4 028 | - | 1 861 | 20 506 |
将表 8的结果与表 3的结果进行比较可知:在根据原始数据识别过程中,堆石料Ⅰ抗剪强度参数服从的最优Copula函数为Plackett Copula, 而通过Bootstrap子样本被识别为最优Copula函数次数最多的是Clayton Copula.而对于其他2种材料而言,通过Bootstrap子样本被识别为最优Copula函数次数最多的结果与单次识别最优的结果一致.
表 8的结果表明,心墙料备选Copula函数AIC值的变异性较大,而堆石料Ⅰ备选Copula函数AIC值的变异性较小,出现这种情况的原因是心墙料的原始试验样本数目较少,而堆石料Ⅰ的原始试验样本数目较多.
3 基于Bootstrap方法的堆石坝坝坡稳定可靠度分析以糯扎渡水电站心墙堆石坝为算例,给出基于Bootstrap的堆石坝坝坡稳定可靠度分析方法.计算过程中的滑动面为图 2所示的最危险滑动面.2种计算情形为:正常蓄水位条件下考虑垂直地震惯性力分别向上(情形1)和向下(情形2).
3.1 仅考虑概率分布参数与相关系数统计不确定性由于堆石坝坝坡稳定可靠度分析中包含了抗剪强度参数边缘分布参数、边缘分布类型、相关系数和相关结构4种不确定性.首先研究分布参数与相关系数这2个数值统计不确定性对于坝坡稳定可靠度分析的影响.各抗剪强度参数的分布类型以及参数间的相关结构将依据表 2和表 3的结果进行固定,认为原始试验数据最能反映边缘分布的分布类型和参数间的相关结构.相关系数由抗剪强度参数子样本确定,分布参数由样本的均值与标准差确定.
基于已知的抗剪强度参数边缘分布函数与Copula函数即可计算边坡的失效概率,Ns个Bootstrap子样本就可以得到Ns个失效概率.每一组Bootstrap子样本通过1.3节介绍的方法进行可靠度分析,获得每组子样本下坝坡的失效概率,从而对一种工况下坝坡的失效情况进行区间估计.
图 4反映了仅考虑分布参数与相关系数统计不确定性情况下,2种情形中基于Bootstrap方法获得的失效概率均值与标准差的收敛情况.从图中可以看出,当计算次数达到30 000次时,2种工况下失效概率的均值和标准差均收敛.

|
| 图 4 仅考虑分布参数与分布类型统计不确定性各统计量收敛性 Fig. 4 Convergence of various statistics in consideration of statistical uncertainties of distribution parameter and distribution type |
同时考虑分布参数、分布类型、相关系数及相关结构统计不确定性对于坝坡稳定分析的影响,对每次抽出的Bootstrap子样本,相关系数由抗剪强度参数子样本确定,分布参数由样本的均值与标准差确定,分布类型的识别以及Copula类型的识别均用AIC准则确定,这样,对于每一组Bootstrap子样本,分布类型与相关结构也依赖于本组子样本的特性.基于已知的抗剪强度参数边缘分布函数与Copula函数即可计算坝坡的失效概率,Ns个Bootstrap子样本就可以得到Ns个失效概率.
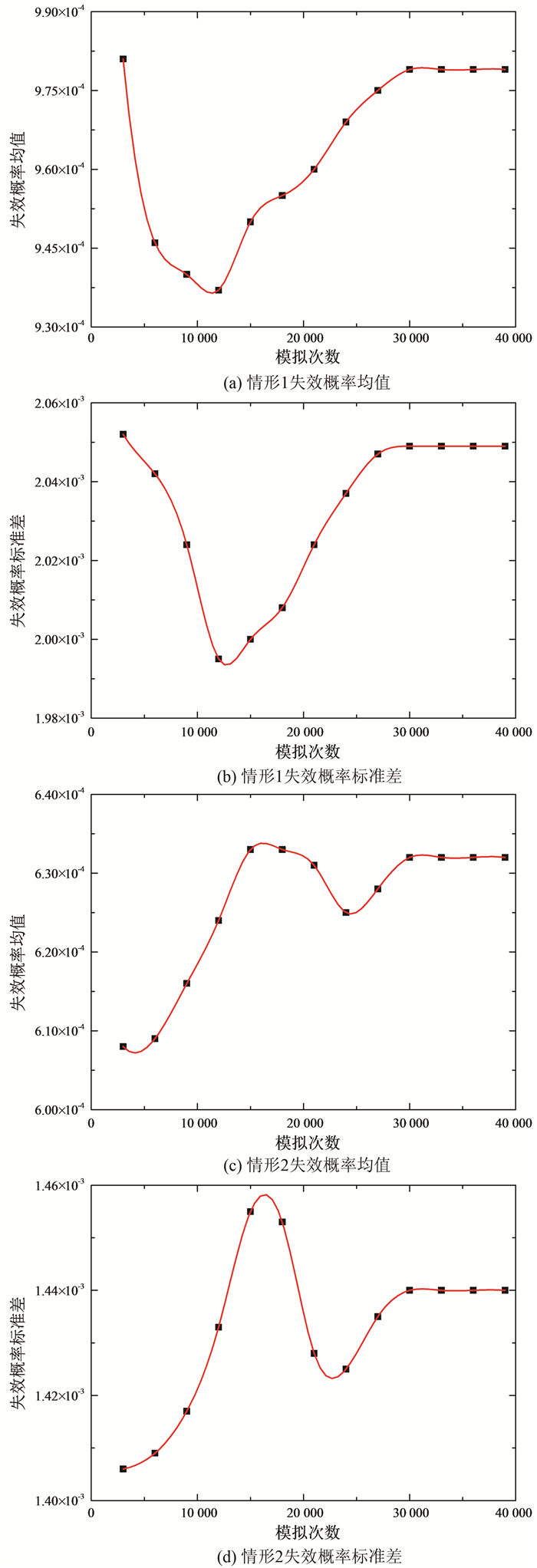
图 5反映了同时考虑边缘分布参数、边缘分布类型、相关系数和相关结构的统计不确定性情况下,基于Bootstrap方法获得的失效概率均值与标准差的收敛情况.从图中可以看出,当计算次数达到30 000次时,2种工况下失效概率的均值和标准差均收敛.
|
| 图 5 同时考虑分布参数、分布类型、相关系数、相关结构不确定性各统计量收敛性 Fig. 5 Convergence of various statistics in consideration of statistical uncertainties of distribution parameter, distribution type, correlation coefficient and correlation type |
为了表征失效概率的变异性,可以用一定置信度水平的置信区间来反映失效概率的分布情况.基于可靠度指标的概率密度函数可以采用多种方法计算出可靠度指标的置信区间.此外,置信区间又包括双侧和单侧置信区间,实际工程可根据具体设计要求加以选择.本文将失效概率的5%和95%分位数值作为失效概率90%双侧置信区间的上下限,结果如表 9所示.
| 计算情形 | 仅考虑分布参数和相关系数统计不确定性 | 考虑分布参数、相关系数、分布类型和相关结构统计不确定性 | ||||||
| 均值 (×10-3) |
标准差 (×10-3) |
变异系数 | 90%置信区间 (×10-3) |
均值 (×10-3) |
标准差 (×10-3) |
变异系数 | 90%置信区间 (×10-3) |
|
| 1 | 1.221 | 2.245 | 1.839 | [0, 3.480] | 1.326 | 2.777 | 2.094 | [0, 4.860] |
| 2 | 0.790 | 1.733 | 2.194 | [0, 2.270] | 0.872 | 1.986 | 2.278 | [0, 3.180] |
将表 9的结果与表 4的结果进行比较可以看出,基于Bootstrap方法的失效概率均值与基于原始数据计算的失效概率接近,说明考虑统计不确定性后的可靠度分析结果是有效的,Bootstrap方法可以有效地反映各变异性导致的统计不确定性的影响,最终以一个区间的形式反映出失效概率可能出现的情况.
将3.1节与3.2节的计算结果进行比较可以发现,全面考虑各种统计不确定性计算的均值要比仅考虑参数统计不确定性计算的均值要大,且给出的区间范围也更大,说明忽略分布类型和相关结构的统计不确定性将高估坝坡的稳定性.这是因为Bootstrap方法充分考虑了不同备选概率分布函数为最优边缘分布以及不同备选Copula函数为最优相关结构的可能性,而传统方法只挖掘了原始数据所携带的信息,没有考虑到小样本对于描述总体信息的局限性.
4 结论1) 基于原始抗剪强度参数试验数据估计的样本均值、标准差、分布函数AIC值、Copula函数AIC值具有较大变异性,这种变异性导致边缘分布函数与Copula函数具有较大统计不确定性.样本数据量较少导致了分布参数与相关系数的不确定性,边缘分布函数与Copula函数的AIC值分别导致了分布类型和相关结构不确定性.
2) Bootstrap方法可以有效地模拟抗剪强度参数的统计不确定性.通过模拟抗剪强度参数的边缘分布参数、边缘分布类型、相关系数、相关结构的统计不确定性,可以将坝坡稳定的失效概率表示为一定置信水平下的置信区间,以区间的形式给出坝坡失效概率的参考值.
3) 抗剪强度参数边缘分布函数与表征相关性的Copula函数的统计不确定性对堆石坝坝坡稳定分析的结果有重要的影响.同时考虑边缘分布参数、边缘分布类型、相关系数与相关结构的统计不确定性分析的失效概率比仅考虑边缘分布参数和相关系数统计不确定性的失效概率变异性更大,均值更大,区间更宽.忽略边缘分布类型和相关结构的统计不确定性将高估坝坡的稳定性.
4) 基于原始抗剪强度参数试验数据获得的失效概率并不能充分反映堆石坝稳定情况.基于原始数据得到的失效概率较Bootstrap模拟结果的均值更小,忽略各类统计不确定性不一定能准确地反映堆石坝稳定的实际状况.基于Bootstrap方法的堆石坝坝坡稳定可靠度分析得到的失效概率区间可以为工程师衡量坝坡实际稳定状况提供参考.
| [1] |
中华人民共和国国家发展和改革委员会. DL/T5395-2007碾压式土石坝设计规范[S].北京: 中国电力出版社, 2008: 47-51, 83-89. National Development and Reform Commission of the People's Republic of China. DL/T5395-2007 Design Specification for Rolled Earth-rock Fill Dams[S]. Beijing: China Electric Power Press, 2008: 47-51, 83-89. |
| [2] |
中华人民共和国水利部. SL274-2001碾压式土石坝设计规范[S].北京: 中国水利水电出版社, 2002: 71-77. Ministry of Water Resources of the People's Republic of China. SL274-2001 Design Code for Rolled Earth-rock Fill Dams[S]. Beijing: China WaterPower Press, 2002: 71-77. |
| [3] |
陈群, 唐岷, 朱分清. 强度参数的不确定性对土石坝坝坡失稳概率的影响[J]. 岩土工程学报, 2008, 30(11): 1594-1599. Chen Qun, Tang Min, Zhu Fenqing. Influence of uncertainty of strength parameters on instability probability of embankment dam slopes[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(11): 1594-1599. DOI:10.3321/j.issn:1000-4548.2008.11.003 |
| [4] |
张明, 刘金勇, 麦家煊. 土石坝边坡稳定可靠度分析与设计[J]. 水力发电学报, 2006, 25(2): 103-107. Zhang Ming, Liu Jinyong, Mai Jiaxuan. Reliability analysis and design of slope stability of earth-rock dam[J]. Journal of Hydroelectric Engineering, 2006, 25(2): 103-107. DOI:10.3969/j.issn.1003-1243.2006.02.022 |
| [5] |
唐小松, 李典庆, 周创兵, 等. 基于Bootstrap方法的岩土体参数联合分布模型识别[J]. 岩土力学, 2015, 36(4): 913-922. Tang Xiaosong, Li Dianqing, Zhou Chuangbing, et al. Bootstrap method for joint probability distribution identification of correlated geotechnical parameters[J]. Rock and Soil Mechanics, 2015, 36(4): 913-922. |
| [6] |
唐小松, 李典庆, 曹子君, 等. 有限数据条件下边坡可靠度分析的Bootstrap方法[J]. 岩土力学, 2016, 37(3): 893-901. Tang Xiaosong, Li Dianqing, Cao Zijun, et al. A Bootstrap method for analyzing slope reliability based on limited shear-strength parameter data[J]. Rock and Soil Mechanics, 2016, 37(3): 893-901. |
| [7] |
吴震宇, 陈建康, 许唯临, 等. 高堆石坝非线性强度指标坝坡稳定可靠度分析方法研究及工程应用[J]. 岩石力学与工程学报, 2009, 28(1): 130-137. Wu Zhenyu, Chen Jiankang, Xu Weilin, et al. Research on methodology of reliability analysis of high rockfill dam slope stability using nonlinear strength indexes and its engineering application[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(1): 130-137. DOI:10.3321/j.issn:1000-6915.2009.01.017 |
| [8] |
Wu Z Y, Chen J K, Li Y L, et al. An algorithm in generalized coordinate system and its application to reliability analysis of seismic slope stability of high rockfill dams[J]. Engineering Geology, 2015, 188: 88-96. DOI:10.1016/j.enggeo.2015.01.019 |
| [9] |
唐小松, 李典庆, 周创兵, 等. 基于Copula函数的抗剪强度参数间相关性模拟及边坡可靠度分析[J]. 岩土工程学报, 2012, 34(12): 2284-2291. Tang Xiaosong, Li Dianqing, Zhou Chuangbing, et al. Modeling dependence between shear strength parameters using Copulas and its effect on slope reliability[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(12): 2284-2291. |
| [10] |
Luo Z, Atamturktur S, Juang C H. Bootstrapping for characterizing the effect of uncertainty in sample statistics for braced excavations[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(1): 13-23. |
| [11] |
Duncan J M, Byrne P M, Wong K S. Strength, stress-strain and bulk modulus parameters for finite element analysis of stress and movements in soil masses (research report No. VCB/GT/78-02)[R]. Berkeley: University of California, 1978.
|
| [12] |
Nelson R B. An Introduction to Copulas[M]. New York: Springer, 2006.
|
| [13] |
Akaike H. A new look at the statistical model identification[J]. IEEE Transactions on Automatic Control, 1974, 19(6): 716-723. DOI:10.1109/TAC.1974.1100705 |
| [14] |
Efron B. Bootstrap methods: another look at the Jackknife[J]. The Annals of Statistics, 1979, 7(1): 1-26. |
 2019, Vol. 52
2019, Vol. 52




