文章信息
- 陈仲民, 樊恒, 向金海, 邓君丽
- CHENG Zhongmin, FAN Heng, XIANG Jinhai, DENG Junli
- 基于稀疏表示的室内指纹定位算法
- An indoor fingerprint location algorithm based on sparse representation
- 武汉大学学报(工学版), 2016, 49(3): 465-468
- Engineering Journal of Wuhan University, 2016, 49(3): 465-468
- http://dx.doi.org/10.14188/j.1671-8844.2016-03-025
-
文章历史
- 收稿日期: 2015-12-02
2. 华中农业大学工学院,湖北 武汉 430070
2. College of Engineering, Huazhong Agricultural University, Wuhan 430070, China
室外定位技术目前最常用的是全球定位系统(Global Position System,GPS),在室外空旷的环境下,GPS的精度能够得到较好的保证[1].然而,由于建筑物的遮挡,卫星信号在室内环境中不能正常传输,导致GPS接收器难以接收到无线信号,无法实现正常的定位和导航功能.
无线WiFi是目前广泛使用的一种移动互联网技术,被部署在很多教学楼、家庭、办公室、商场等室内环境中.同时,随着计算机技术的发展,智能移动终端的成本不断降低,移动互联网在人们日常生活中得到普及,使得利用WiFi技术进行室内定位具有可操作强、成本低以及覆盖性广等优点,被广泛应用在自动化、自动行走技术[2]、地理信息处理技术[3]及作为其他定位系统的辅助部分[4].
1 基于无线网络技术的室内定位算法目前,基于无线网络的室内定位算法主要分为3种:几何法[5]、近似法[6]和场景分析法[7].Wang等人[8]对信号的衰减进行建模,得到了信号传播的距离与强度的关系,并通过模拟实验建立了信号穿墙的损失函数.根据目标所获得的无线信号强度,可以估计出其位置,从而实现定位.但是,这种方法需要严格控制室内环境的无线网络部署,限制了其适用性.Battiti等人[9]通过使用统计学习理论建立接收信号强度(Receive Signal Strength Indication,RSSI)与位置的关系模型来实现室内目标定位,但是他们的实验只在小范围内进行,样本较少,不具有普遍性.De Moraes等人[10]提出了一种无须离线训练的WiFi定位方法,定位精度可达到2 m左右,但是这种方法定位区域大小有限,因此推广困难.桑楠等人[11]提出了一种基于SVM分类和回归的WiFi室内定位方法,该方法对室内区域进行分割,形成多个相互独立的小区域,使用支持向量机建立每个区域的接收信号强度和位置的非线性模型,并以此来对待测点的位置进行估计.但是,当室内存在较多的障碍物时,这种方法得到的RSSI与位置的非线性关系并不准确,定位误差较大.Chen等人[12]提出使用卡尔曼滤波算法建立RSSI和位置的关系,并以此实现目标的定位.
目前,位置指纹[13]被广泛用于室内定位算法中.这类算法主要包含两个阶段:离线阶段指纹采集及在线阶段指纹匹配.离线阶段,采集参考点从接入点(Access Point,AP)所接收的RSSI,并将这些RSSI按特定的顺序存放,构成该参考点的位置指纹.采集所有参考点处的位置指纹,并建立位置指纹数据库存放所有参考点的位置指纹及其对应的坐标信息.在线阶段,获取待测点处的位置指纹,并将其与指纹数据库中的位置指纹进行匹配,用匹配所得到的位置指纹所对应的坐标信息来对待测点的位置进行估计,从而实现定位.从指纹匹配的角度来看,定位问题可被转换为一个多分类问题.
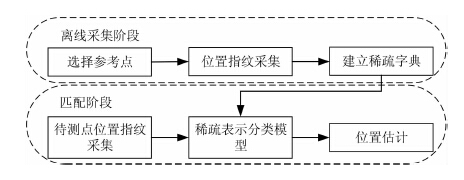
近来,稀疏表示[14]因对信号重构的高效性和准确性,被广泛用于计算机视觉领域,如目标检测[15]、目标跟踪[16]、图像分类[17]等.基于此,本文提出了一种基于位置指纹和稀疏表达的WiFi室内定位算法.在离线采集阶段,首先在待测区域内选取若干参考点,对于每个参考点,多次测量其位置指纹,作为该位置训练样本的位置指纹,并将所有参考点的位置指纹组成稀疏字典.在匹配阶段,首先获取待测点的位置指纹,根据待测点位置指纹在稀疏字典上投影的不同将待测点与参考点进行匹配,从而对其位置进行估计.算法流程图如图 1所示.
|
| 图 1 基于稀疏表达的室内定位算法流程图 Figure 1 Flowchart of proposed localization method based on sparse representation |
在室内区域内部署m个AP,并选取N个参考点.对于第n (n=1,2,…,N)个参考点采集m个AP的信号强度形成一个M维矢量作为指纹信息f:
其中:f为第n个参考点的指纹矢量;si为第i个AP的信号强度.在第n个参考点上采集p次指纹,组成的矩阵可以表示该位置的指纹库Fn:
其中:fj(j=1,2,…,p)表示第n个参考点上第j次采集的指纹.将N个参考点的位置指纹组成数据字典:
式中:Fn表示N个参考点位置的指纹库;A为N个参考点的数据字典.
3 基于稀疏表示的室内定位算法待测点的指纹信息y可表示为如下形式:
其中:x表示待测点的指纹信息在数据字典上的投影系数.如果待测点的指纹信息与第n个参考点的位置指纹匹配,则其投影系数中只有与第n个参考点指纹库相关的系数不为零.这表明,y的投影系数x具有稀疏性.根据文献[18],可通过解l1优化问题来求解稀疏解:
但是,在实际问题中通常存在噪声,需加入误差阈值,可将式(5)改写为
式中:x*为x的近似值;ε是误差阈值.对式(6)进行求解,得到了x的近似解x*.然而,建模误差和噪声的存在,使得投影系数x并不是理想值.为判别待测点所属的指纹库,定义向量δn(x*)为向量x*中只与第n个参考点的指纹库相关的非零行.因此,若y属于第n个参考点的指纹库,则y的近似值可表示如下:
其中,y*n表示y在第n个参考点指纹库上的近似值.两者差值越小,y与第n个参考点指纹库相匹配的可能性越高,采用如下判别函数:
如何求解l1最小化范数是稀疏表示的关键.Deedell等人[19]提出了一种ROMP算法.对稀疏度为K的信号,若余量与字典相关系数为g∈RM×1,选出K个最大的相关系数存入候选集J,将J进行分组,对于任意分组Q,若满足所有i,j∈Q,则
选择能量最大的一组子集Q作为最终的索引值集,选取该索引值集对应的原子集λQ,根据最小二乘法计算信号逼近x′及更新余量rnew:
传统的ROMP算法需要把信号的稀疏度作为求解条件,而信号的稀疏度往往是未知的.为此,文献[20]对传统ROMP算法进行了改进,提出了一种正则化二次筛选正交匹配追踪算法,该算法不需要预知信号的稀疏度,且求解速度比传统ROMP更快.
4 实验 4.1 仿真实验本文首先利用仿真实验对算法的性能进行估计.信号强度通过常用的对数距离路径损耗模型进行模拟:
式中:γ表示多径衰弱,服从Rayleigh分布;p0为1m处的信号强度,p0=-45dbm;n为路径损耗指数,n=2.326;ξ为阴影衰弱,服从均值为0、标准差为5.2的正态分布.
参考点的位置指纹由接入点的个数决定.一般地,接入点越多,位置指纹所包含的信息越丰富,定位结果越精确,但随之定位成本也将提高.本文采用不同个数的接入点进行仿真试验,结果见图 2.

|
| 图 2 不同个数的接入点仿真实验结果 Figure 2 Simulation results using different numbers of APs |
从图 2中可知,接入点个数越多,定位精度越高.接入点数量达到一定后,定位精度趋于稳定.综合考虑定位精度和成本,本文算法使用9个接入点.
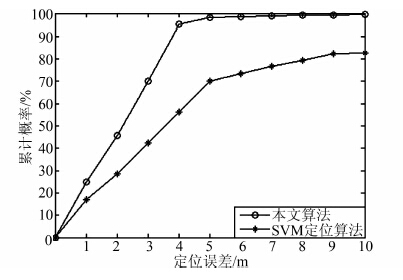
4.2 实验环境实验场地设置在面积为144 m2的开放教学楼(12 m×12 m),包含2个走廊、4个教室,每个教室包含2条走道和若干排座位.离线采集阶段,将整个区域均匀分割为1m×1m的单元格,在每个单元格中心采集位置指纹10次,用于构建数据字典.指纹匹配阶段,在实验场地随机选取600个待测点,并测量位置指纹,使用本文算法来估计待测点的位置.为了更好验证算法性能,将本文算法与基于SVM的定位算法[21]进行比较.本文算法中需要确定的参数为重构的误差阈值ε,设置为ε=0.15.比较结果如图 3所示.由图 3可知,本文算法在定位误差为2m和4 m时的累计概率分别为45.7%和95.3%,明显优于SVM定位算法.
|
| 图 3 定位精度 Figure 3 Positioning accuracy |
为了取得较好的定位结果,SVM中的多个参数需要进行多次调解和优化,而且所得到的分类器并不能综合利用全局参考点的信息,导致最终的定位结果不够精确.本文提出的基于稀疏表示指纹定位算法能够充分利用位置指纹冗余信息,对待测点的位置指纹进行重构,并根据重构的误差来对待测点所属类别进行有效分类,从而实现定位.此外,本文算法只需要确定误差阈值,不需要对参数进行多次优化,提高了定位效率.
5 结论本文提出的一种基于稀疏表示的室内定位算法,可以有效实现室内定位.首先在室内区域选择若干个参考点,多次测量参考点从接入点接收到的WiFi信号强度,构建稀疏数据字典.通过稀疏表示方法,用参考点的指纹矢量对待测点处的指纹矢量进行重构,根据重构误差来估计待测点的位置.实验结果表明,本文方法能够有效实现室内定位.
| [1] | Peters S W, Heath R W. Interference alignment via alternation minimization [C] // Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing, 2009: 2445-2448. |
| [2] | Biswas J, Veloso M. WiFi localization and navigation for autonomous indoor mobile robots [C] // Proceedings of IEEE International Conference on Robotics and Automation, 2010: 4379-4384. |
| [3] | Kawaguchi N, Yano M, Ishida S, et al. Underground positioning: subway information system using WiFi location technology [C] // Proceedings of the 10th International Conference on Mobile Data Management: Systems, Services and Middleware, 2009: 371-372. |
| [4] | Woodman O, Harle R. Pedestrian localization for indoor environment [C] // Proceedings of the 10th International Conference on Ubiquitous Computing, 2008: 114-123. |
| [5] | Yamasaki R, Ogino A, Tamaki T. TDOA location system for IEEE 802.11b WLAN [C] // Proceedings of Wireless Communications and Networking Conference, 2005: 2338-2343. |
| [6] | Lamarca A, Chawathe Y, Consolvo S, et al. PlaceLab: device positioning using radio beacons in the wild [C] // Proceedings of the 3rd International Conference on Pervasive Computing, 2005: 116-133. |
| [7] | Bahl P, Padmanabhan V N. RADAR: an in-building RF-based location and tracking system [C] // Proceedings of IEEE INFOCOM, 2000: 775-784. |
| [8] | Wang Y, Jia X, Lee H K, et al. An indoor wireless positioning system based on wireless local area network infrastructure [C] // Proceedings of the 6th International Symposium on Satellite Navigation Technology Including Mobile Positioning and Location Services, 2003: 21-34. |
| [9] | Battiti R, Brunato M, Villani A. Statistical learning theory for location fingerprinting in wireless LANs[J]. Computer Networks: the International Journal of Computer and Telecommunications Networking, 2005, 47(6): 825–845. |
| [10] | De Moraes L F M, Nunes B A A. Calibration-free WLAN location system based on dynamic mapping of signal strength [C] // Proceedings of the 4th ACM International Workshop on Mobility Management and Wireless Access, 2006: 92-99. |
| [11] |
桑楠, 袁兴中, 周瑞. 基于SVM分类和回归的WiFi室内定位方法[J].
计算机应用研究, 2014, 31(6): 1820–1823.
Sang N, Yuan X Z, Zhou R. Method of WiFi location based on SVM[J]. Application Research of Computer, 2014, 31(6): 1820–1823. |
| [12] | Chen Z M, Fan H. The research and improvement of indoor localization algorithms based on RSSI [C] // Proceedings of the International Conference on Computer Science and Network Technology, 2013: 178-181. |
| [13] |
曾伟, 黄亮. 一种基于稀疏表示的WLAN室内定位算法[J].
计算机应用与软件, 2014, 31(12): 175–178.
Zeng W, Huang L. A sparse representation-based WLAN indoor positioning algorithm[J]. Computer Applications and Software, 2014, 31(12): 175–178. |
| [14] | Wright J, Yang A Y, Ganesh A, et al. Robust face recognition via sparse representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(2): 210–227. DOI:10.1109/TPAMI.2008.79 |
| [15] | Zhou W, Fei M, Zhou H, et al. A sparse representation based fast detection method for surface defect detection of bottle caps[J]. Neurocomputing, 2014, 123: 406–414. DOI:10.1016/j.neucom.2013.07.038 |
| [16] |
向金海, 樊恒, 徐俊, 等. 基于局部稀疏表示的目标跟踪[J].
华中科技大学学报(自然科学版), 2014, 42(7): 92–95.
Xiang J H, Fan H, Xu J, et al. Object tracking based on local sparse representation[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2014, 42(7): 92–95. |
| [17] |
向金海, 杨申, 樊恒, 等. 基于稀疏表示的烤烟烟叶品质分级研究[J].
农业机械学报, 2013, 44(11): 287–292.
Xiang J H, Yang S, Fan H, et al. Grading for tobacco leaf quality based on sparse representation[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(11): 287–292. |
| [18] | Candes E, Romberg J, Tao T. Stable signal recovery from incomplete and inaccurate measurements[J]. Communication on Pure and Applied Mathematics, 2006, 59(8): 1207–1223. DOI:10.1002/(ISSN)1097-0312 |
| [19] | Needell D, Vershynin D. Uniform uncertainly principle and signal recovery via regularized orthogonal matching pursuit[J]. Foundations of Computational Mathematics, 2009, 9(3): 317–334. DOI:10.1007/s10208-008-9031-3 |
| [20] |
王燕霞, 张弓. 一种改进的用于稀疏表示的正交匹配追踪算法[J].
信息与电子工程, 2012, 10(5): 579–583.
Wang Y X, Zhang G. An improved orthogonal matching pursuit algorithm for sparse representation[J]. Information and Electronic Engineering, 2012, 10(5): 579–583. |
| [21] | Brunato M, Battiti R. Statistical learning theory for location fingerprinting in wireless LANs[J]. Computer Networks, 2005, 47(6): 825–845. DOI:10.1016/j.comnet.2004.09.004 |
 2016, Vol. 49
2016, Vol. 49




