文章信息
- 吴倩, 纪磊, 喻莹, 王誉博, 龚庆武
- WU Qian, JI Lei, YU Ying, WANG Yubo, GONG Qingwu
- 基于粒子群优化的改进原子分解法的直击雷故障识别方法
- Identification of direct lightning fault based on PSO improved atomic decomposition
- 武汉大学学报(工学版), 2018, 51(7): 620-626, 633
- Engineering Journal of Wuhan University, 2018, 51(7): 620-626, 633
- http://dx.doi.org/10.14188/j.1671-8844.2018-07-009
-
文章历史
- 收稿日期: 2018-03-11
2. 国网临沂供电公司, 山东 临沂 276000;
3. 湖北省电力公司检修公司,湖北 武汉 430050;
4. 武汉大学电气工程学院, 湖北 武汉 430072
2. State Grid Linyi Power Supply Company, Linyi 276000, China;
3. Maintenance Company, Hubei Power Company, Wuhan 430050, China;
4. School of Electrical Engineering, Wuhan University, Wuhan 430072, China
雷击是造成输电线路故障的主要原因之一[1, 2].因此,国内外电力工作者一直关注输电线路防雷研究[3].
输电线路的雷击故障分为两种:一种是感应雷故障,另外一种是直击雷故障.由于输电线路的绝缘水平较高,感应雷造成故障的可能性一般较小,因此,重点是直击雷故障[4].雷电直击输电线路又分为绕击和反击,二者的故障机理不同,相应的防雷措施也不尽相同.人们不能准确地判定雷击故障是反击还是绕击,从而导致在采取防雷措施时盲目、被动,防雷效果大大降低,雷击故障跳闸率一直居高不下.
如果通过行波测距装置[5, 6]获得雷电数据,然后利用该数据,对故障进行识别和精确定位,准确地分析出雷击类型并对相应的故障做出处理,这对于输电线路防雷工作的开展以及防雷措施评价具有重要意义.
随着在线监测技术和暂态信号分析方法的不断发展,输电线路雷击故障识别问题得到越来越多学者的关注,研究成果丰富.文献[6]提出了一套诊断系统来识别非雷击故障和雷击故障,但是并没有给出具体方法的解释,只是定性分析,而且在最后的应用中只是给出了数据的结果,并没有陈述数据如何得到.文献[7]提出利用小波变换,根据模极大值的极性以及避雷器的持续放电时间识别反击与绕击过电压,但是小波变换不能根据信号本身的特征自适应地表示信号,而且存在频域混叠现象.文献[8]提出了用直线对雷击后的行波进行拟合,采用波形相似系数区别轻型雷击与弱雷击故障的方法,但是该文献是从保护动作的角度考虑雷击故障,并不是从防雷的角度对雷击进行分类.文献[9]只提出了感应雷的识别方法,对直击雷故障的识别没有进行深入研究.
为此,本文将一种新兴的分析非线性、非平稳信号的方法——原子分解法用于雷电反击和绕击的识别中.原子分解法克服了传统线性化方法不能对非平稳信号进行分析的缺点,也不存在小波等传统方法的诸多不足.雷电中信号成分繁多,采用现有的小波变换等方法不能很好地分析相近的高频暂态分量,而原子分解法恰好可以解决这种问题.因为原子分解法的分解策略是贪婪的、自适应的,由于有高度过完备的原子库,从而保证任意信号都能够自适应地选择一组最佳匹配原子进行表征.本文在建立ATP-EMTP同塔双回输电线路仿真模型的基础上,对500 kV输电线路的雷电过电压进行大量的电磁暂态仿真,对雷击引起的绕击和反击故障暂态特征进行分析和对比,并且根据两种判据的整定值来识别直击雷的故障类型.仿真结果表明,本文所提方法能够有效地识别直击雷故障的类型,并且解决了传统方法频率分辨率不高、自适应性不强的缺点.
1 原子分解的基本原理 1.1 原子分解基本概念Mallat和Zhang提出了信号在过完备原子库(Over-Complete Dictionary)上进行分解的思想[10],在N维Hilbert空间H中,构建一个超完备的展开函数集合Ddic={gγ, γ=1, 2, …, Ldic},集合Ddic为原子库,gγ为由参数组γ定义的原子,对于一个具体的信号,可根据自身特征自适应地从集合Ddic中选择最佳的一组原子来展开,使分解结果变得非常稀疏,从而得到信号非常简洁的表达,此过程称为稀疏分解(Sparse Decomposition)[11].
近年来,原子分解技术在信号处理领域的应用越来越广泛,如语音信号[12]、雷达信号[13]、电力系统信号[14-16]等领域.原子分解的核心问题是如何构建一个合理的原子库以及如何自适应地寻找最佳匹配原子及其参数,目前已经发展了多种稀疏分解算法和多种原子库类型,如Gabor原子[17]、Chirp原子[18]、正弦原子[19]等原子库.
1.2 基于PSO的MP算法为了得到信号的原子分解结果,常采用匹配追踪(Matching Pursuits, MP)算法[10].MP算法是一种贪婪迭代算法,经算法迭代后任何信号都可以分解成:
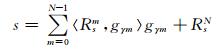 (1)
(1)
其中:s为待分析的信号; gγm为第m个原子;Rsm为残余信号;RsN为第N次迭代计算后的信号残差.分解后的残余信号Rsm随着m的增大而迅速减小,对于长度有限的数字信号来说,Rsm随m的增大而指数衰减为0,因此,当忽略信号残差时,信号s可近似表达为
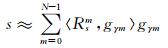 (2)
(2)
由式(1)、式(2)可以看出每一步分解都需要进行大量的内积运算,计算时间过长,限制了原子分解法的实用性.实际上MP算法寻找最佳匹配原子就是一个求解最优值的问题,因此可以利用粒子群优化算法(Particle Swarm Optimization, PSO)[20]对其进行优化求解以减少计算量.具体步骤参看文献[20].
2 基于原子分解法的雷击故障识别方法 2.1 根据原子分解能量比值构造判据雷击故障和一般短路故障相比,由于雷电流的侵入,在频谱能量分布上高频能量占的比重要大很多;反击故障和绕击故障相比,高频能量占的比重大一些[21].原子分解法每次提取的最佳匹配原子是与原始信号内积最大、最为匹配的原子,通过设置合理的迭代次数,就能使残余信号的能量忽略不计,提取的原子很好地表征原始信号.由于是基于高频能量比重提出判据,需要提取表征高频暂态分量的最佳匹配原子的频率、幅值、匹配度等特征参数.
定义电流的总能量:
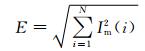
其中:N为分析电流的采样点数;Im为所有频率分量的幅值.
定义相对高频分量的能量:
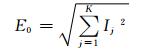
其中:K为原子分解提取出的高频分量的总个数,定义频率大于300 Hz为相对高频分量; Ij为提取出的高频分量的幅值.
显然电流总能量的计算过程不涉及原子分解.为了更好地提取高频分量,先对线模电流进行滤波处理.在信号分析中加入冲激响应滤波器(Filter Impulse Response, FIR),滤除频率低于300 Hz的成分后再进行原子分解.那么相对高频分量的能量占电流总能量的比值为
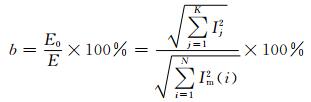 (3)
(3)
结合以上分析,根据原子分解能量比值的雷击故障识别算法步骤如下:
1) 当判断为接地故障后,计算电流线模分量.
2) 对线模分量进行FIR滤波.
3) 取故障后5 ms线模电流分量进行原子分解法分析,分解迭代次数设为50次,采样频率1 MHz,提取频率大于300 Hz的最佳匹配原子的特征参量并存储到数据库.
4) 计算相对高频分量的能量E0和电流总能量E.
5) 根据式(3)计算相对高频分量的能量占电流总能量的比值b.
6) 若b < k1,则判定为一般短路故障,若b>k2,判定为反击短路故障,否则判定为绕击短路故障.阈值k1与k2根据实际情况进行整定.
2.2 根据故障相电流行波电磁暂态特征构造判据由故障相电流行波暂态特征分析可知,单相接地短路故障时,故障时刻的电源电压决定了故障暂态行波电流的波尾时间,行波波尾时间要比雷击故障时长很多,而且故障暂态行波电流衰减缓慢,所以可以考虑将波尾时间和衰减系数作为识别雷击和非雷击故障的判据;绕击故障和反击故障相比,在整个绕击过程中,不会出现和雷电流反向的电磁耦合电流,因此可以根据反极性感应脉冲的有无识别反击和绕击故障.原子分解法可以直接将给定信号进行最佳匹配原子的分解,得到各个原子的匹配度G、幅值A、频率f、相位φ、起始时刻t1、终止时刻t2以及衰减因子s,对上述问题的分析非常适合.对故障相电流暂态分量进行原子分解,得到若干个最佳匹配原子,这些最佳匹配原子主要对应着由工频闪络引起的暂态分量和雷电流造成的暂态分量,体现了故障信号最显著、最重要的信息,由于判据是故障暂态行波电流的波尾时间和反极性感应脉冲的有无,只需要提取最佳匹配原子频率、匹配度、衰减因子、起始时刻和终止时刻5项参数,并进行比较即可进行故障性质识别.识别方案如下:
1) 如果提取的最佳匹配原子中匹配度最大的表征高频暂态成分的原子,起始时刻和终止时刻间隔超过某一阈值,则判断为非雷击故障,否则判定为雷击故障.
2) 判定为雷击故障后,如果提取的最佳匹配原子中有表征反极性感应脉冲的原子存在,则判定为反击故障,否则判定为绕击故障.
原子分解是对信号的主要局部特征进行匹配,对故障后前50 μs内故障相电流暂态行波运用原子分解法进行分析,得到的最佳匹配原子中在去除频率低于1 000 Hz的原子后,记匹配度最大的原子匹配度为G1、频率为f1、开始时间为t11、终止时间为t12.终止时间和开始时间的时间差即可认为是行波波头时间.对于雷击故障,该原子即为表征闪络后雷电流前行波的原子,而且该方法还能准确捕捉到反击和绕击暂态行波波头起始位置的差异.记其余最佳匹配原子中频率最大的原子(即有可能表征闪络前反极性感应脉冲的原子)频率为fmax、起始时间为tx1、终止时间为tx2.定义识别判据:
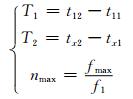 (4)
(4)
构造基于上述判据的识别算法,具体步骤和流程如下:
1) 当判断为接地故障并确定故障相后,对数据库中的故障相电流进行基于PSO改进的原子分解,数据窗取故障后50 μs,分解迭代次数设为5次,采样频率为1 MHz.
2) 在去除频率低于1 000 Hz的原子后,提取表征电流行波暂态特征的最佳匹配原子的频率、匹配度等特征量信息,并将这些特征量信息存储到数据库中.
3) 根据式(4)计算各个判据.
4) 如果T1=t12-t11>tset1,则判定为一般短路故障,否则判定为雷击故障.
5) 判定为雷击故障后,如果在用原子分解法分解得到的最佳匹配原子中存在原子x,满足T2=tx2-tx1 < tset2,且
tset1与tset2以及nset根据实际情况进行整定.
3 仿真实例分析搭建ATP-EMTP模型进行仿真分析,仿真步长10 ns,仿真时间为40 ms,10 ms时距离N端150 km发生故障.各种故障的仿真条件设置如下:雷击杆塔故障,雷电流200 kA,造成A相绝缘子发生闪络短路故障,即反击故障;雷击导线故障,雷电流为30 kA,造成A相绝缘子发生闪络故障,即绕击故障;接地短路,A相经100 Ω过渡电阻接地短路故障,即工频闪络.
根据大量的仿真实验,对各个判据整定如表 1所示.
| 判据整定值 | 判定结果 |
| b < 1% & T1>20 μs | 工频闪络故障 |
| 1% < b < 5% & T1 < 20 μs | 绕击故障 |
| b>5% & T1 < 20 μs & nmax>10 & T2 < 1.2 μs |
反击故障 |
| Others | 判据失效 |
利用K变换将线路保护处采集的三相故障电流行波解耦,得到线模电流如图 1~3所示.由图 1~3可知,线模电流中含有大量的急剧衰减的高频成分,在故障后前5 ms内高频成分幅值较大.

|
| 图 1 雷击杆塔故障线模电流波形图 Fig. 1 Waveform of mode current on lightning pole tower fault line |

|
| 图 2 雷击导线故障线模电流波形图 Fig. 2 Waveform of mode current on lightning wire fault line |

|
| 图 3 A相工频闪络故障线模电流波形图 Fig. 3 Waveform of mode current on phase A industrial flashover fault line |
用编制的原子分解算法程序对线模电流进行分析.故障点距离监测点150 km,波形传到监测点需要大约0.5 ms,而故障时间为10 ms,因此大约在10.5 ms才能采集到故障电流,采样时间为5 ms,因此设置采样时间为10.5~15.5 ms.采用原子分解对线模电流进行处理,先对数据进行降低采样频率处理,采样频率变为1 MHz,分解次数设为30次,原子分解提取的主要频率分量及其幅值如表 2~4所示.
| 频率/Hz | 幅值/A |
| 104.049 1 | 345.217 3 |
| 339.420 8 | 1 448.408 1 |
| 1 459.026 0 | 512.650 1 |
| 5 540.054 2 | 553.076 5 |
| 6 590.352 5 | 684.219 4 |
| 7 099.681 5 | 1 217.837 5 |
| 7 468.985 4 | 1 015.680 9 |
| 8 247.282 3 | 1 603.931 3 |
| 14 345.345 4 | 557.321 8 |
| 频率/Hz | 幅值/A |
| 281.251 6 | 67.337 4 |
| 583.869 3 | 122.907 6 |
| 828.268 0 | 282.877 9 |
| 1 683.909 0 | 77.628 0 |
| 2 317.474 2 | 1 050.059 9 |
| 6 940.541 8 | 521.640 0 |
| 8 070.775 8 | 465.250 3 |
| 频率/Hz | 幅值/A |
| 297.544 4 | 54.123 2 |
| 822.332 4 | 265.886 6 |
| 1 430.214 9 | 23.311 5 |
| 1 865.016 8 | 121.646 1 |
| 2 903.412 0 | 47.302 8 |
| 6 834.682 1 | 130.160 9 |
原子分解法计算得到的各特征参数精确到小数点后4位,分析表 2~4的数据可以看出,一般的工频短路故障的故障电流主要由故障相接地引起的工频电弧产生的低频分量组成,高频分量非常小.而雷击故障的故障电流的高频分量很大,其中雷击导线的高频分量的含量稍微比雷击杆塔的高频分量小.因此可利用以上差别区分雷击故障与一般故障.
通过仿真得到单相短路故障以及雷电反击和绕击故障时故障相暂态电流波形如图 4所示.按照原子分解法分析信号的流程,对故障相暂态电流进行分析,发现当设置迭代次数为10次时,后面5次迭代所产生的匹配原子的内积值相对很小,可以不予考虑,迭代次数设置为5次就能很好地体现信号的每个局部特征.因此根据经验设置迭代次数为5次.

|
| 图 4 故障相暂态电流波形图 Fig. 4 Transient current waveforms of fault phases |
迭代完成后,根据每次迭代的适应度值,对5次迭代所得的最佳匹配原子进行取舍,去除频率低于1 MHz的成分后,选择出最合适的几个最佳匹配原子,对结果观察发现第2次和第3次分解出的原子与原始信号最相关,其他几次迭代内积值很小可忽略不计.因此,把算法得到的第2次和第3次最佳匹配原子的参数转化为信号的局部特征参量,就能最好地表征信号的特征,表 5为得到的最佳匹配原子的特征参量.
| 故障类型 | 原子序号 | 适应度值 | 频率/Hz | 衰减系数 | 开始时间/μs | 终止时间/μs |
| 反击故障 | 1 | 0.101 6 | 74 061 | 424.43 | 7.102 | 8.494 |
| 2 | 0.034 0 | 2 062 441 | 2 082.10 | 6.302 | 7.008 | |
| 绕击故障 | 1 | 0.451 6 | 40 733 | 2 636.40 | 5.777 | 7.775 |
| 工频闪络 | 1 | 0.017 2 | 23 292 | 5 464.10 | 6.190 | 50.000 |
识别判据计算结果如表 6所示,能可靠地将3种故障类型识别出来.
| 识别判据 | b/% | T1/μs | nmax | T2/μs |
| 工频闪络 | 0.66 | 43.0 | - | - |
| 反击故障 | 13.42 | 1.4 | 27.85 | 0.703 |
| 绕击故障 | 2.32 | 2.0 | - | - |
超高压输电线路发生各类接地故障时,故障情况复杂,尤其是发生雷击故障时,系统的暂态特征量变化剧烈.所提判据受多种条件的影响,以计算能量比值的数据窗选择为例,接地故障发生后,随着时间的推移,高频分量不断地衰减,而工频稳态分量可以认为一直不变,故数据窗越长,相对高频分量所占电流总能量的比值越小,如表 7所示,不同故障类型之间的判据差异逐渐变小,所以数据窗不宜过长.
| 取样时间/ms | 1 | 2 | 3 | 5 | 20 | |
| 能量比/% | 雷击杆塔 | 30.16 | 24.32 | 16.49 | 13.42 | 8.72 |
| 雷击导线 | 10.87 | 5.37 | 3.25 | 2.32 | 1.18 | |
| 工频故障 | 2.45 | 1.62 | 1.14 | 0.66 | 0.42 | |
为了讨论故障初相角对该判据的影响,设置不同的故障初相角, 即0°、30°、45°、60°、90°,所得结果如表 8所示.故障初相角对工频短路故障时的判据整定影响较大,这是因为高频成分的幅值在故障初相角为零度时最小,即如果在电势过零瞬间发生工频短路,此时电容电压为零,高频电流是电感中存储的能量向电容充电造成的.
| 初相角/(°) | 0 | 30 | 45 | 60 | 90 | |
| 能量比/% | 雷击杆塔 | 13.42 | 13.48 | 13.55 | 13.61 | 13.74 |
| 雷击导线 | 2.32 | 2.37 | 2.39 | 2.46 | 2.51 | |
| 工频故障 | 0.66 | 0.68 | 0.73 | 0.78 | 0.85 | |
用编制的原子分解算法程序对反击故障后前50 μs内的故障相电流暂态行波进行分析,根据原子分解法5次迭代的结果,可以得到经过分解后的重构信号.图 5为原始信号与重构信号以及经过原子分解完成后的残余信号对比分析图.分析可知,经过原子分解法5次迭代得到的最佳匹配原子和原始信号非常吻合,精确度高,残余信号很小,可以忽略不计,即认为重构信号有效表示出了原始信号.

|
| 图 5 原始信号与重构信号以及残余信号对比分析图 Fig. 5 Comparison of original and reconstructed signals and residual signals |
下面再针对各种故障情况进行全面的仿真分析来验证本文所提识别方法的可靠性.仿真模型同上,以雷电流幅值来表示不同的雷击状态,具体情况如表 9所示.普通短路故障选取不同的故障初相角和过渡电阻.仿真结果如表 10所示.
| 雷电流幅值I0/kA | 雷击状态 |
| 8 | 雷电绕击导线未故障 |
| 12 | 雷电绕击导线未故障 |
| 60 | 雷电直击杆塔未故障 |
| 90 | 雷电直击杆塔未故障 |
| 20 | 绕击故障 |
| 35 | 绕击故障 |
| 120 | 反击故障 |
| 250 | 反击故障 |
| 类型 | G50 | b/% | T1/μs | nmax | T2/μs | 识别结果 | |
| 2.6/50 μs | I0=8 kA | 0 | - | - | - | - | 雷击干扰 |
| I0=12 kA | 0 | - | - | - | - | ||
| I0=60 kA | 0 | - | - | - | - | ||
| I0=90 kA | 0 | - | - | - | - | ||
| I0=20 kA | 0.987 | 2.15 | 1.998 | 0 | - | 绕击故障 | |
| I0=35 kA | 0.982 | 2.46 | 2.003 | 0 | - | ||
| I0=120 kA | 0.975 | 11.13 | 1.287 | 29.81 | 0.651 | 反击故障 | |
| I0=250 kA | 0.968 | 13.64 | 1.415 | 25.34 | 0.717 | ||
| 4/100 μs | I0=8 kA | 0 | - | - | - | - | 雷击干扰 |
| I0=12 kA | 0 | - | - | - | - | ||
| I0=60 kA | 0 | - | - | - | - | ||
| I0=90 kA | 0 | - | - | - | - | ||
| I0=20 kA | 0.983 | 2.37 | 3.199 | 0 | - | 绕击故障 | |
| I0=35 kA | 0.976 | 2.58 | 3.206 | 0 | - | ||
| I0=120 kA | 0.971 | 11.57 | 2.013 | 28.34 | 0.396 | 反击故障 | |
| I0=250 kA | 0.962 | 14.02 | 2.238 | 26.60 | 0.553 | ||
| 单相接地 | 0.992 | 0.52 | 43.823 | - | - | 普通单相接地 | |
| 0.989 | 0.49 | 43.768 | - | - | |||
| 0.985 | 0.72 | 43.819 | - | - | |||
| 0.990 | 0.68 | 43.771 | - | - | |||
1) 雷击故障的故障电流的频谱能量不仅含有绝缘子击穿后造成的稳定工频电弧所带有的低频能量,还含有由雷电流引起的高频能量;而一般的工频短路故障的故障电流的成分主要由故障相接地引起的工频电弧产生的低频分量组成,高频分量非常小.
2) 通过对故障相的电流波形暂态特征分析可知,单相接地短路故障时,故障时刻的电源电压决定了故障暂态行波电流的波尾时间,行波波尾时间要比雷击故障时间长很多,而且故障暂态行波电流衰减缓慢,所以可以考虑将波尾时间和衰减系数作为识别雷击和非雷击故障的判据;绕击故障和反击故障相比,在整个绕击过程中,不会出现和雷电流反向的电磁耦合电流,因此可以根据反极性感应脉冲的有无识别反击和绕击故障.
3) 在ATP-EMTP软件中建立了500 kV同塔双回输电线路仿真模型,对普通故障、反击故障以及绕击故障进行了仿真,分析了故障相和非故障相电流的波形特点,找出了反击和绕击故障相电流的波形差异,验证了理论分析的正确性.
| [1] |
陈慈萱. 电气工程基础(下册)[M]. 北京: 中国电力出版社, 2004: 354-360. Chen Cixuan. Electrical Engineering Foundation (volume below)[M]. Beijing: China Electric Power Press, 2004: 354-360. |
| [2] |
Uman M A. The Lightning Discharge[M]. USA: Aca- demic San Diego, 1987.
|
| [3] |
吴昊, 肖先勇, 沈睿佼. 小波能量谱和神经网络法识别雷击与短路故障[J]. 高电压技术, 2007, 33(10): 64-68. Wu Hao, Xiao Xianyong, Shen Ruijiao. Lightning strike and fault identification by the wavelet energy spectrum and neural network method[J]. High Voltage Engineering, 2007, 33(10): 64-68. DOI:10.3969/j.issn.1003-6520.2007.10.015 |
| [4] |
吴健儿. 浅谈输电线路雷击绕击与反击[J]. 浙江电力, 2007, 26(4): 43-46. Wu Jianer. Discussion on lightning shielding failure and counterattack of transmission lines[J]. Zhejiang Electric Power, 2007, 26(4): 43-46. |
| [5] |
彭向阳, 钱冠军, 王红斌, 等. 利用CVT响应电流实现变电站雷电入侵在线监测[J]. 电网技术, 2011, 35(7): 203-207. Peng Xiangyang, Qian Guanjun, Wang Hongbin, et al. On-line monitoring of lightning surge intruding into substation by current response of busbar capacitor voltage transformer[J]. Power System Technology, 2011, 35(7): 203-207. |
| [6] |
彭向阳, 钱冠军, 李鑫, 等. 架空输电线路跳闸故障智能诊断[J]. 高电压技术, 2012, 38(3): 1965-1972. Peng Xiangyang, Qian Guanjun, Li Xin, et al. Intelligent trip-out fault diagnosis of overhead transmission line[J]. High Voltage Engineering, 2012, 38(3): 1965-1972. |
| [7] |
司马文霞, 谢博, 杨庆, 等. 特高压输电线路雷电过电压的分类识别方法[J]. 高电压技术, 2010, 36(2): 306-312. Sima Wenxia, Xie bo, Yang Qing, et al. Identification of lightning over-voltage about UHV transmission line[J]. High Voltage Engineering, 2010, 36(2): 306-312. |
| [8] |
吕艳萍, 刘亚东. 应用数学形态学方法分析识别特高压线路雷击干扰[J]. 高电压技术, 2010, 36(12): 2948-2953. Lü Yanping, Liu Yadong. New scheme to identify lightning for UHV transmission line using mathematical morphology[J]. High Voltage Engineering, 2010, 36(12): 2948-2953. |
| [9] |
李海峰, 王钢, 赵建仓. 输电线路感应雷击暂态特征分析及其识别方法[J]. 中国电机工程学报, 2004, 24(3): 114-119. Li Haifeng, Wang Gang, Zhao Jiancang. Study on characteristics and identification of transients on transmission lines caused by indirect lightning stroke[J]. Proceedings of the CSEE, 2004, 24(3): 114-119. DOI:10.3321/j.issn:0258-8013.2004.03.021 |
| [10] |
Mallat S, Zhang Z. Matching pursuits with time frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397-3415. DOI:10.1109/78.258082 |
| [11] |
Coifman R R, Wickerhauser M V. Entropy-based algorithms for best basis selection[J]. IEEE Transactions on Information Theory, 1992, 38(2): 713-718. DOI:10.1109/18.119732 |
| [12] |
朱明, 普运伟, 金炜东, 等. 基于时频原子方法的雷达辐射源信号特征提取[J]. 电波科学学报, 2007, 22(3): 458-462. Zhu Ming, Pu Yunwei, Jin Weidong, et al. Feature extraction of radar emitter signals based on time-frequency atoms[J]. Chinese Journal of Radio Science, 2007, 22(3): 458-462. DOI:10.3969/j.issn.1005-0388.2007.03.020 |
| [13] |
武明勤, 于凤芹. 基于Chirp原子分解的语音信号时频结构分析[J]. 江南大学学报(自然科学版), 2006, 5(6): 685-687. Wu Mingqin, Yu Fengqin. A time frequency analysis method for speech signal based on Chirp atoms decomposition[J]. Journal of Southern Yangtze University(Natural Science Edition), 2006, 5(6): 685-687. DOI:10.3969/j.issn.1671-7147.2006.06.013 |
| [14] |
李勋, 龚庆武, 贾晶晶. 采用原子分解能量熵的低频振荡主导模式检测方法[J]. 中国电机工程学报, 2012, 32(1): 131-139. Li Xun, Gong Qingwu, Jia Jingjing. A detection method for low frequency oscillation dominant modes based on atomic decomposition energy entropy[J]. Proceedings of the CSEE, 2012, 32(1): 131-139. |
| [15] |
贾清泉, 于连富, 董海艳, 等. 应用原子分解的电能质量扰动信号特征提取方法[J]. 电力系统自动化, 2009, 33(24): 61-64. Jia Qingquan, Yu Lianfu, Dong Haiyan, et al. Power quality disturbance features extraction based on atomic decomposition[J]. Automation of Electric Power Systems, 2009, 33(24): 61-64. |
| [16] |
王宁, 李林川, 贾清泉, 等. 应用原子分解的电能质量扰动信号分类方法[J]. 中国电机工程学报, 2011, 31(4): 51-58. Wang Ning, Li Linchuan, Jia Qingquan, et al. Classification of power quality disturbance signals using atomic decomposition method[J]. Proceedings of the CSEE, 2011, 31(4): 51-58. |
| [17] |
Troppj A. Greed is good: algorithmic results for sparse approximation[J]. IEEE Transactions on Information Theory, 2004, 50(10): 2231-2242. DOI:10.1109/TIT.2004.834793 |
| [18] |
Gribonval R. Fast matching pursuit with a multiscale dictionary of Gaussian Chirps[J]. IEEE Transactions on Signal Processing, 2001, 49(5): 994-1001. |
| [19] |
Lovisolo L, Eduardo A B da S, Marco A M R, et al. Efficient coherent adaptive representations of monitored electric signals in power systems using damped sinusoids[J]. IEEE Transactions on Signal Processing, 2005, 53(10): 3831-3846. |
| [20] |
李勋, 龚庆武, 关钦月, 等. 基于PSO的模态原子法在低频振荡模式时变特性追踪中的应用[J]. 中国电机工程学报, 2013, 33(10): 79-89. Li Xun, Gong Qingwu, Guan Qinyue, et al. PSO based modal atom method and its application to track time-varying performance of low frequency oscillation modes[J]. Proceedings of the CSEE, 2013, 33(10): 79-89. |
| [21] |
关根志. 高电压工程基础[M]. 北京: 中国电力出版社, 2003: 153-157. Guan Genzhi. High Voltage Engineering Foundation[M]. Beijing: China Electric Power Press, 2003: 153-157. |
 2018, Vol. 51
2018, Vol. 51




